Какое количество информации содержится, к примеру, в тексте романа "Война и мир", во фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро.

А возможно ли объективно измерить количество информации? Важнейшим результатом теории информации является вывод:

В определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных.

В настоящее время получили распространение подходы к определению понятия "количество информации", основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте.

Так, американский инженер Р. Хартли (1928 г.) процесс получения информации рассматривает как выбор одного сообщения из конечного, наперед заданного, множества из N равновероятных сообщений, а количество информации 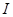, содержащееся в выбранном сообщении, определяет как двоичный логарифм . Формула Хартли:

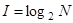
Приведем примеры равновероятных сообщений:

1. при бросании монеты: "выпала решка", "выпал орел";

2. на странице книги: "количество букв чётное", "количество букв нечётное".

Определим теперь, являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.

Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.

Формула Шеннона:

,

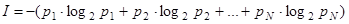где 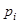 - вероятность того, что именно 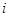-е сообщение выделено в наборе из  сообщений.

Легко заметить, что если вероятности 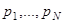 равны, то каждая из них равна , и формула Шеннона превращается в формулу Хартли.

В качестве единицы информации условились принять один бит (англ. bit — binary, digit — двоичная цифра).

Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений.

А в вычислительной технике битом называют наименьшую "порцию" памяти, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд.

Бит — слишком мелкая единица измерения. На практике чаще применяется более крупная единица — байт, равная восьми битам. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2⁸).

На базе 8-разрядного двоичного кода в настоящее время существует множество систем кодирования. При создании первых версий IBM PC, которые работали только под управлением ОС MS DOS, была разработана кодировка ASCII (American Standard Code for Information Interchange – Американский стандартный код обмена информацией), содержащая латинские буквы, знаки препинания, скобки, специальные знаки и пробел.

Стандартный код ASCII включает:

· латинские строчные буквы 'А'...'Z' – порядковые номера в ASCII-таблице 65 – 90, прописные латинские буквы 'а'...'z' – порядковые номера 97 – 122;

· цифровые знаки '0'...'9' – порядковые номера 48–57;

· знаки препинания, специальные символы и пробел, например, '+', '/', '*', '%' и др.;

· управляющие коды, которые используются для разделения информации при ее кодировании и управлении работой внешних устройств компьютера.

В настоящее время разработана двухбайтная кодировка Unicode, которую поддерживает операционная система Windows NT. Коды символов в этой кодировке могут принимать значения от 0 до 65535.

Широко используются также ещё более крупные производные единицы информации:

· 1 Килобайт (Кбайт) = 1024 байт = 2¹⁰ байт,

· 1 Мегабайт (Мбайт) = 1024 Кбайт = 2²⁰ байт,

· 1 Гигабайт (Гбайт) = 1024 Мбайт = 2³⁰ байт.

В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:

· 1 Терабайт (Тбайт) = 1024 Гбайт = 2⁴⁰ байт,

· 1 Петабайт (Пбайт) = 1024 Тбайт = 2⁵⁰ байт.

За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации.