Основные элементарные функции и их графики. Примеры показательной и степенной функции.
Основными элементарными функциями являются
§ постоянная функция (константа),
§ корень n-ой степени, степенная функция,
§ показательная,
§ тригонометрические и обратные тригонометрические функции,
§ логарифмическая функция.
Постоянная. 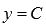

Свойства постоянной функции.
· Область определения: все множество действительных чисел.
· Постоянная функция является четной.
· Область значений: множество, состоящее из единственного числа С.
· Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
· Говорить о выпуклости и вогнутости постоянной не имеет смысла.
· Асимптот нет.
· Функция проходит через точку (0,C) координатной плоскости.
Корень n-ой степени, степенная функция. 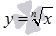
1. n - четное число.

Свойства функции корень n-ой степени при четных n.
· Область определения: множество всех неотрицательных действительных чисел 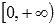 .
.
· При x=0 функция 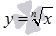 принимает значение, равное нулю.
принимает значение, равное нулю.
· Эта функция общего вида (не является четной или нечетной).
· Область значений функции: 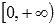 .
.
· Функция 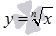 при четных показателях корня возрастает на всей области определения.
при четных показателях корня возрастает на всей области определения.
· Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
· Асимптот нет.
· График функции корень n-ой степени при четных n проходит через точки (0,0) и(1,1).
2. n - нечетное число.
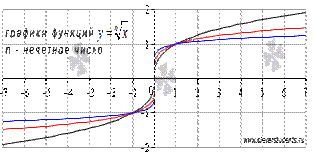
Свойства функции корень n-ой степени при нечетных n.
· Область определения: множество всех действительных чисел.
· Эта функция нечетная.
· Область значений функции: множество всех действительных чисел.
· Функция 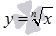 при нечетных показателях корня возрастает на всей области определения.
при нечетных показателях корня возрастает на всей области определения.
· Эта функция вогнутая на промежутке 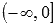 и выпуклая на промежутке
и выпуклая на промежутке 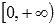 , точка с координатами (0,0) – точка перегиба.
, точка с координатами (0,0) – точка перегиба.
· Асимптот нет.
· График функции корень n-ой степени при нечетных n проходит через точки (-1,-1),(0,0) и (1,1).
Степенная. 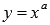
1. а - нечетное число, а>0

Свойства степенной функции с нечетным положительным показателем.
· Область определения:  .
.
· Область значений: 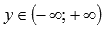 .
.
· Функция нечетная, так как 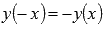 .
.
· Функция возрастает при  .
.
· Функция выпуклая при 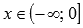 и вогнутая при
и вогнутая при 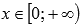 (кроме линейной функции).
(кроме линейной функции).
· Точка (0;0) является точкой перегиба (кроме линейной функции).
· Асимптот нет.
· Функция проходит через точки (-1;-1), (0;0), (1;1).
2. а - четное число, а>0

Свойства степенной функции с четным положительным показателем.
· Область определения:  .
.
· Область значений: 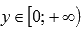 .
.
· Функция четная, так как 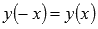 .
.
· Функция возрастает при 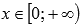 , убывает при
, убывает при 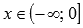 .
.
· Функция вогнутая при  .
.
· Точек перегиба нет.
· Асимптот нет.
· Функция проходит через точки (-1;1), (0;0), (1;1).
3. а - нечетное число, а<0
Свойства степенной функции с нечетным отрицательным показателем.
· Область определения: 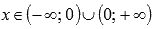 . При x=0 имеем разрыв второго рода, так как
. При x=0 имеем разрыв второго рода, так как 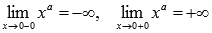 приа=-1,-3,-5,…. Следовательно, прямая x=0 является вертикальной асимптотой.
приа=-1,-3,-5,…. Следовательно, прямая x=0 является вертикальной асимптотой.
· Область значений: 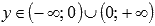 .
.
· Функция нечетная, так как 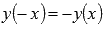 .
.
· Функция убывает при 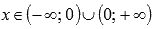 .
.
· Функция выпуклая при 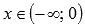 и вогнутая при
и вогнутая при 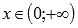 .
.
· Точек перегиба нет.
· Горизонтальной асимптотой является прямая y = 0, так как 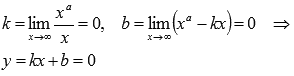 при а=-1,-3,-5,….
при а=-1,-3,-5,….
· Функция проходит через точки (-1;-1), (1;1).
4. а - четное число, а<0
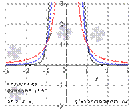
Свойства степенной функции с четным отрицательным показателем.
· Область определения: 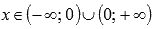 . При x=0 имеем разрыв второго рода, так как
. При x=0 имеем разрыв второго рода, так как 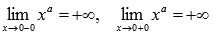 приа=-2,-4,-6,…. Следовательно, прямая x=0 является вертикальной асимптотой.
приа=-2,-4,-6,…. Следовательно, прямая x=0 является вертикальной асимптотой.
· Область значений:  .
.
· Функция четная, так как 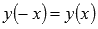 .
.
· Функция возрастает при 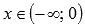 , убывает при
, убывает при 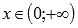 .
.
· Функция вогнутая при 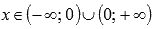 .
.
· Точек перегиба нет.
· Горизонтальной асимптотой является прямая y=0, так как 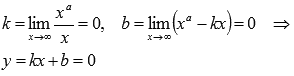 при а=-2,-4,-6,….
при а=-2,-4,-6,….
· Функция проходит через точки (-1;1), (1;1).
Показательная.  , где
, где 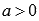 ,
, 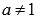 .
.
1. 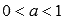
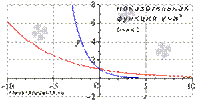
Свойства показательной функции с основанием меньшим единицы.
· Областью определения показательной функции является все множество действительнйх чисел:  .
.
· Область значений:  .
.
· Функция не является ни четной, ни нечетной, то есть, она общего вида.
· Показательная функция, основание которой меньше единицы, убывает на всей области определения.
· Функция вогнутая при  .
.
· Точек перегиба нет.
· Горизонтальной асимптотой является прямая y = 0 при х стремящемся к плюс бесконечности.
· Функция проходит через точку (0;1).
2. 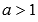
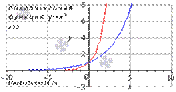
Свойства показательной функции с основанием большим единицы.
· Область определения показательной функции:  .
.
· Область значений:  .
.
· Функция не является ни четной, ни нечетной, то есть она общего вида.
· Показательная функция, основание которой больше единицы, возрастает при  .
.
· Функция вогнутая при  .
.
· Точек перегиба нет.
· Горизонтальной асимптотой является прямая y = 0 при х стремящемся к минус бесконечности.
· Функция проходит через точку (0;1).
Тригонометрические и обратные тригонометрические. 
1. Синусоида. y = sin(x)
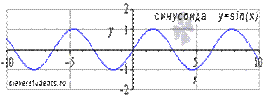
Свойства функции синус y = sin(x).
· Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при  .
.
· Наименьший положительный период функции синуса равен двум пи: 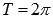 .
.
· Функция обращается в ноль при 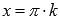 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть 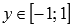 .
.
· Функция синус - нечетная, так как 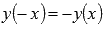 .
.
· Функция убывает при 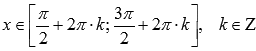 , возрастает при
, возрастает при 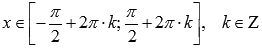 .
.
· Функция синус имеет локальные максимумы в точках 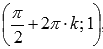 , локальные минимумы в точках
, локальные минимумы в точках 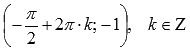 .
.
· Функция y = sinx вогнутая при 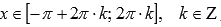 , выпуклая при
, выпуклая при 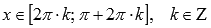 .
.
· Координаты точек перегиба 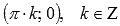 .
.
· Асимптот нет.
2. Косинусоида. y = cos(x)
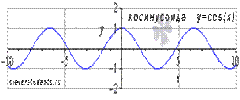
Свойства функции косинус y = cos(x).
· Область определения функции косинус:  .
.
· Наименьший положительный период функции y = cosx равен двум пи: 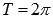 .
.
· Функция обращается в ноль при 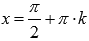 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции косинус представляет интервал от минус единицы до единицы включительно: 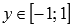 .
.
· Функция косинус - четная, так как 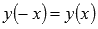 .
.
· Функция убывает при 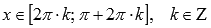 , возрастает при
, возрастает при 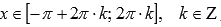 .
.
· Функция y = cosx имеет локальные максимумы в точках 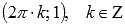 , локальные минимумы в точках
, локальные минимумы в точках 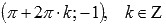 .
.
· Функция вогнутая при 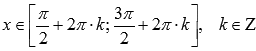 , выпуклая при
, выпуклая при 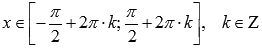 .
.
· Координаты точек перегиба  .
.
· Асимптот нет.
3. Тангенсоида. y = tg(x).
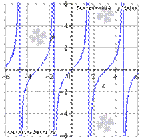
Свойства функции тангенс y = tg(x).
· Область определения функции тангенс: 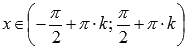 , где
, где  , Z – множество целых чисел. Поведение функции y = tgx на границе области определения
, Z – множество целых чисел. Поведение функции y = tgx на границе области определения 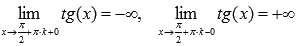 Следовательно, прямые
Следовательно, прямые 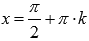 , где
, где  , являются вертикальными асимптотами.
, являются вертикальными асимптотами.
· Наименьший положительный период функции тангенс  .
.
· Функция обращается в ноль при 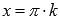 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции y = tg(x): 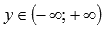 .
.
· Функция тангенс - нечетная, так как 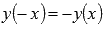 .
.
· Функция возрастает при 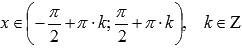 .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при 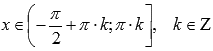 .
.
· Координаты точек перегиба 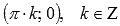 .
.
· Наклонных и горизонтальных асимптот нет.
4. Котангенсоида. y = ctg(x)
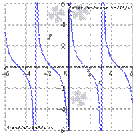
Свойства функции котангенс y = ctgx.
· Область определения функции котангенс: 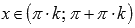 , где
, где  , Z – множество целых чисел. Поведение на границе области определения
, Z – множество целых чисел. Поведение на границе области определения 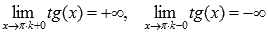 Следовательно, прямые
Следовательно, прямые 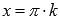 , где
, где  являются вертикальными асимптотами.
являются вертикальными асимптотами.
· Наименьший положительный период функции y = ctgx равен пи:  .
.
· Функция обращается в ноль при 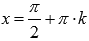 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции котангенс: 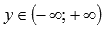 .
.
· Функция нечетная, так как 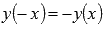 .
.
· Функция y = ctg(x) убывает при 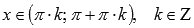 .
.
· Функция котангенс вогнутая при 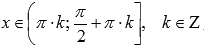 , выпуклая при
, выпуклая при  .
.
· Координаты точек перегиба  .
.
· Наклонных и горизонтальных асимптот нет.
5. Арксинусоида. y = arcsin(x)

Свойства функции арксинус y = arcsin(x).
· Областью определения функции арксинус является интервал от минус единицы до единицы включительно: 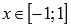 .
.
· Область значений функции y = arcsin(x): 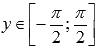 .
.
· Функция арксинус - нечетная, так как 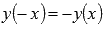 .
.
· Функция y = arcsin(x) возрастает на всей области определения, то есть, при 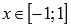 .
.
· Функция вогнутая при 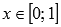 , выпуклая при
, выпуклая при  .
.
· Точка перегиба (0; 0), она же ноль функции.
· Асимптот нет.
6. Арккосинусоида. y = arccos(x)

Свойства функции арккосинус y = arccos(x).
· Область определения функции арккосинус: 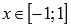 .
.
· Область значений функции y = arccos(x): 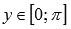 .
.
· Функция не является ни четной ни нечетной, то есть, она общего вида.
· Функция арккосинус убывает на всей области определения, то есть, при 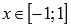 .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при 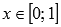 .
.
· Точка перегиба  .
.
· Асимптот нет.
7. Арктангенсоида. y = arctg(x)
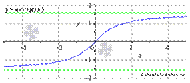
Свойства функции арктангенс y = arctg(x).
· Область определения функции y = arctg(x):  .
.
· Область значений функции арктангенс: 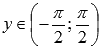 .
.
· Функция арктангенс - нечетная, так как 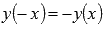 .
.
· Функция возрастает на всей области определения, то есть, при  .
.
· Функция арктангенс вогнутая при 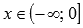 , выпуклая при
, выпуклая при 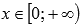 .
.
· Точка перегиба (0; 0), она же ноль функции.
· Горизонтальными асимптотами являются прямые  при
при 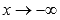 и
и 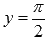 при
при 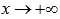 . На чертеже они показаны зеленым цветом.
. На чертеже они показаны зеленым цветом.
8. Арккотангенсоида. y = arcctg(x)
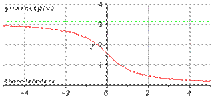
Свойства функции арккотангенс y = arcctg(x).
· Областью определения функции арккотангенс является все множество действительных чисел:  .
.
· Область значений функции y = arcctg(x): 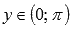 .
.
· Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
· Функция убывает на всей области определения, то есть, при  .
.
· Функция вогнутая при 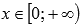 , выпуклая при
, выпуклая при 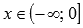 .
.
· Точка перегиба  .
.
· Горизонтальными асимптотами являются прямые 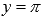 при
при 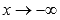 (на чертеже показана зеленым цветом) и y = 0 при
(на чертеже показана зеленым цветом) и y = 0 при 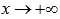 .
.
Логарифмическая  , где
, где 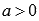 ,
, 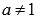 .
. 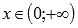
1. 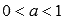
Свойства логарифмической функции с основанием меньшим единицы.
· Область определения логарифмической функции: 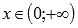 . При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности.
. При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности.
· Область значений: 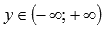 .
.
· Функция не является ни четной, ни нечетной, то есть она общего вида.
· Логарифмическая функция убывает на всей области определения.
· Функция вогнутая при 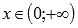 .
.
· Точек перегиба нет.
· Горизонтальных асимптот нет.
· Функция проходит через точку (1;0).
2. 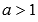

Теоремы о пределах.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
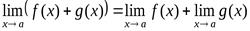
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
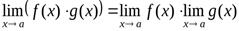 .
.
Следствие 1 . Постоянный множитель можно выносить за знак предела:
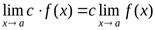 .
.
Следствие 2 . Предел степени равен степени предела:
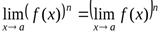 .
.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
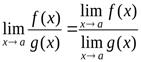 , если
, если 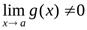 .
.
Методы раскрытия неопределенностей.
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.
1. Разложение числителя и знаменателя на множители с последующим сокращением
2. Деление многочлена на многочлен
3. Устранение иррациональных разностей домножением на сопряженное выражение
4. Замена переменной
5. Первый замечательный предел
6. Правило Лопиталя
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа 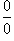 или
или  . Пусть a является некоторым конечным действительным числом или равно бесконечности.
. Пусть a является некоторым конечным действительным числом или равно бесконечности.
· Если 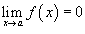 и
и 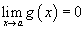 , то
, то 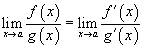 ;
;
· Если 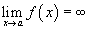 и
и 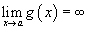 , то аналогично
, то аналогично 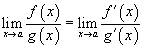 .
.
Правило Лопиталя можно также применять к неопределенностям типа  . Первые две неопределенности
. Первые две неопределенности 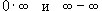 можно свести к типу
можно свести к типу 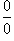 или
или  с помощью алгебраических преобразований. А неопределенности
с помощью алгебраических преобразований. А неопределенности 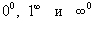 сводятся к типу
сводятся к типу 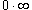 с помощью соотношения
с помощью соотношения
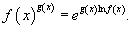
Правило Лопиталя справедливо также и для односторонних пределов.
3. Понятие производной. Геометрический и физический смысл производной.
Произво́дная функции в точке — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
1. Физический смысл производной.
Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная 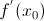 – скорость изменения переменной y относительно переменной x в точке
– скорость изменения переменной y относительно переменной x в точке 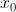 .
.
Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная 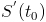 – скорость в момент времени
– скорость в момент времени 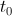 .
.
Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то 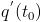 – скорость изменения количества электричества в момент времени
– скорость изменения количества электричества в момент времени 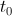 , т.е. сила тока в момент времени
, т.е. сила тока в момент времени 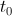 .
.
2. Геометрический смысл производной.
Пусть 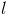 – некоторая кривая,
– некоторая кривая, 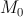 – точка на кривой
– точка на кривой 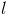 .
.
Любая прямая, пересекающая 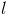 не менее чем в двух точках называется секущей.
не менее чем в двух точках называется секущей.
Касательной к кривой 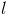 в точке
в точке 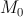 называется предельное положение секущей
называется предельное положение секущей 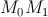 , если точка
, если точка 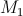 стремится к
стремится к 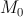 , двигаясь по кривой.
, двигаясь по кривой.
Если касательная к кривой в точке 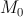 существует, то она единственная.
существует, то она единственная.
4. Применение пределов для нахождения производных элементарных функций. Производные основных элементарных функций.
5. Основные правила дифференцирования. Дифференцирование сложной функции. Привести пример.
Теорема 1. Если функции  и
и 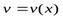 дифференцируемы в данной точке, то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых:
дифференцируемы в данной точке, то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых:
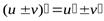 .
.
Формула обобщается на случай любого конечного числа слагаемых.
Теорема 2. Если функции 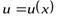 и
и 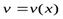 дифференцируемы в данной точке х, то в этой же точке дифференцируемо и их произведение, при этом:
дифференцируемы в данной точке х, то в этой же точке дифференцируемо и их произведение, при этом:
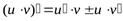 .
.
Следствие. Постоянный множитель можно выносить за знак производной:
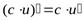 , где
, где 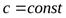 .
.
Теорема 3. Если в данной точке х функции 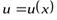 и
и 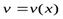 дифференцируемы и
дифференцируемы и 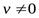 , то в той же точке дифференцируемо и их частное, причем
, то в той же точке дифференцируемо и их частное, причем
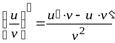 .
.
Производная сложной функции.
Если 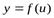 и
и 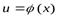 , то
, то 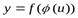 есть сложная функция независимого аргумента x с промежуточным аргументом u.
есть сложная функция независимого аргумента x с промежуточным аргументом u.
Теорема. Если 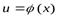 имеет производную
имеет производную  в точке x, а функция
в точке x, а функция 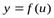 имеет производную
имеет производную 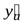 в соответствующей точке u, то сложная функция
в соответствующей точке u, то сложная функция  в данной точке x имеет производную
в данной точке x имеет производную 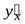 , которая находится по следующей формуле
, которая находится по следующей формуле 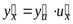 .
.
Часто пользуются следующей формулировкой этой теоремы: производная сложной функции равна произведению производной внешней функции по промежуточному аргументу на производную внутренней функции по независимому аргументу.
Сложная функция может быть составлена не из двух функций, а из большого их числа. В таких случаях теорема применяется последовательно несколько раз.
В частности, если функция 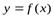 такова, что
такова, что 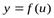 ,
, 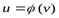 ,
, 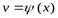 , то производная
, то производная  находится по формуле
находится по формуле 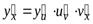 .
.
Пример:
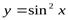 . Здесь у = u2; u=sin x. Тогда
. Здесь у = u2; u=sin x. Тогда
 .
.
6. Понятие первообразной функции и неопределенного интеграла, свойства. Графическое изображение.
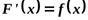
Функция  называется первообразной функцией для функции
называется первообразной функцией для функции  на интервале
на интервале  , если
, если 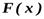 дифференцируема на интервале
дифференцируема на интервале  и
и 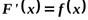 .
.
Если функция имеет первообразную, то она имеет бесконечное множество первообразных.
Произвольная первообразная для 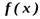 на
на  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 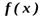 и обозначается символом
и обозначается символом

Знак 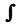 называется интегралом,
называется интегралом,
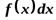 - подынтегральное выражение,
- подынтегральное выражение,
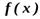 - подынтегральная функция.
- подынтегральная функция.
Таким образом, если 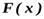 одна из первообразных для
одна из первообразных для  , то
, то


Свойства неопределенного интеграла:
1. 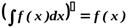
2. 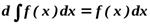
3. 
4. 
7. Нахождение первообразной функции. Пример. Простейшие методы интегрирования.
Операцию нахождения неопределенного интеграла называют интегрированием функции 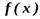 . Она противоположна операции дифференцирования.
. Она противоположна операции дифференцирования.
Пример.
Найти 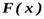 , если
, если 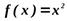 .
.
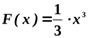 ;
; 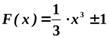 ; и т.д.
; и т.д.
В общем случае  .
.
Или
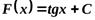 . Или
. Или 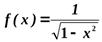
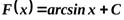
Простейшие способы интегрирования.
а) Непосредственное интегрирование.
Нахождение интегралов функций, основанное на прямом применении свойств неопределенных интегралов и таблицы основных формул интегрирования.
Пример:
∫(х–3)2dх= ∫(х2–6х+9)dх= ∫х2dх- 6∫хdх+9∫dх= х3∕3 -3 х2+9х+С.
б) Интегрирование подстановкой (замена переменной).
Интегрирование подстановкой, или как его часто называют, методом замены переменой, является одним из более эффективных и распространенных методов интегрирования.
Способ подстановки состоит в том, чтобы перейти от данной переменной интегрирования к другой переменной с целью упростить подынтегральное выражение и привести его к одному из табличных видов интегралов.
При этом выбор подстановки решается исполнителем индивидуально, т.к. не существует общих правил, указывающих какую подстановку в данном случае взять.
Пример:
Найти интеграл ∫е2х+3dх.
Введем новую переменную t, связанную с х следующей зависимостью 2х+3=t.
Возьмем дифференциалы от левой и правой частей этого равенства: 2dх=dt;dх=dt/2.
Теперь вместо 2х+3иdх в подинтегральное выражение подставим их значения. Тогда получим: ∫е2х+3dх=  ∫еtdt=
∫еtdt=  еt + С. Возвращаясь к прежней переменной, получим окончательно выражение:
еt + С. Возвращаясь к прежней переменной, получим окончательно выражение:
∫е2х+3dх=  е2х+3 + С.
е2х+3 + С.
8. Понятие определенного интеграла, свойства. Геометрический смысл определенного интеграла. Формула Ньютона – Лейбница.
Пусть функция 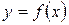 определена на
определена на 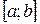 .
.
Разобьём 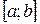 произвольным образом точками
произвольным образом точками 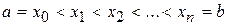 на
на  частичных отрезков длиной
частичных отрезков длиной 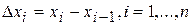 . Выберем в каждом из них произвольно точку
. Выберем в каждом из них произвольно точку 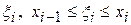 и найдем значения функции в каждой из этих точек
и найдем значения функции в каждой из этих точек 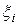 , то есть
, то есть  .
.
Сумма вида
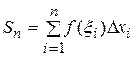 (5.1)
(5.1)
называется n-ой интегральной суммой функции 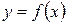 на
на 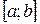 .
.
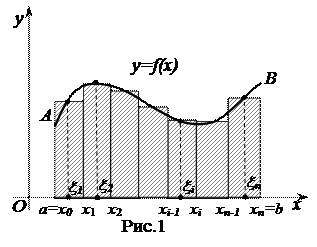
Геометрический смысл интегральной суммы – сумма площадей прямоугольников с основаниями 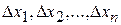 и высотами
и высотами 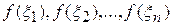 .
.
Обозначим через 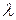 длину наибольшего частичного отрезка данного разбиения
длину наибольшего частичного отрезка данного разбиения 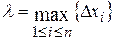 . Найдем предел интегральной суммы
. Найдем предел интегральной суммы  , когда
, когда 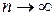 так, что
так, что 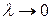 .
.
Если существует конечный предел 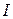 суммы (5.1), не зависящий от способа разбиения отрезка
суммы (5.1), не зависящий от способа разбиения отрезка 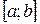 на частичные отрезки и выбора в них точек
на частичные отрезки и выбора в них точек 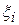 , то этот предел называется определённым интегралом от функции
, то этот предел называется определённым интегралом от функции 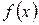 по отрезку
по отрезку 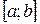 и обозначается:
и обозначается: 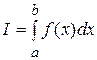 .
.
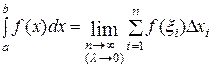
,
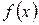 – подынтегральная функция,
– подынтегральная функция,
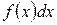 – подынтегральное выражение,
– подынтегральное выражение,
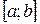 – отрезок интегрирования,
– отрезок интегрирования,
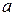 и
и 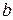 – нижний и верхний пределы интегрирования,
– нижний и верхний пределы интегрирования,
 – переменная интегрирования.
– переменная интегрирования.
Свойства.
1) Если переставить пределы интегрирования, то изменится лишь знак:
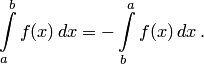
2) Каковы бы ни были а и b, всегда имеет место равенство:

3) Постоянный множитель А выносится за знак определенного интеграла:
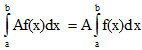
4) Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций:
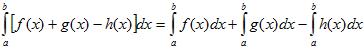
5) Если f(x) – неотрицательная на [a;b], функция и нижний предел меньше верхнего предела (a<b), то и сам интеграл – число неотрицательное, т.е.:
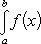

Замечание: если f(x) ≤0 на [a;b] и a<b, то 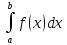 ≤0
≤0
Если f(x) ≥0 на [a;b] и a>b имеем 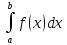 ≤0
≤0
Если f(x) ≤0 на [a;b], то 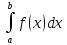 ≥0
≥0
6) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то:
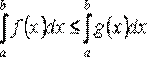 , т.е. неравенство почленно интегрируется.
, т.е. неравенство почленно интегрируется.
7) Если a ≤ b и f(x) непрерывна на [a, b], то:
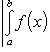
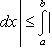
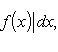 , т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.
, т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.
8) Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a;b], то:
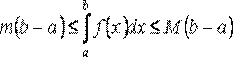
9) Теорема о среднем:
Если функция f(x) непрерывна на [a;b], то существует хотя бы одна точка С на этом отрезке, такая, что справедливо равенство:
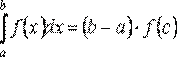
Замечание: формула справедлива также для a>b, кроме a<b
Если a>b, то:
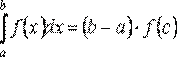 , (b=<c=<a)
, (b=<c=<a)
Геометрический смысл:
Если f(x) >=0 на отрезке [a;b], то интеграл левой части есть площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), а правая часть – площадь прямоугольника с тем же основанием и h=f(c). Для площади криволинейной трапеции всегда есть равновеликий ей прямоугольник с тем же основанием и h, равной ординате этой кривой.
10) Определенный интеграл с одинаковыми пределами равен 0.
 =0
=0
Формула Ньютона - Лейбница
Если f(x) непрерывна на отрезке [a;b], и F(x) - некоторая первообразная функции f(x), То:
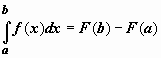
Формулу Ньютона-Лейбница обычно записывают так:
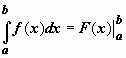
9. Основные определения теории обыкновенных дифференциальных уравнений. Применение дифференциального исчисления для решения прикладных задач биологии и медицины.
10. Случайные события и их классификация. Понятие непрерывной и дискретной случайной величины.
Случайной величиной называется переменная величина, значение которой зависит от исхода некоторого испытания.
Дискретной называется случайная величина, которая может принимать значения некоторой конечной или бесконечной числовой последовательности (число таблеток в упаковке, больных в палате, студентов в аудитории ...).
Непрерывной называется случайная величина, которая может принимать любые значения внутри некоторого интервала (масса, температура, рост ..).
11. Основные положения теории вероятности. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула полной вероятности.
12. Характеристики случайных величин: (математическое ожидание, дисперсия, среднее квадратическое отклонение).
Математическое ожидание дискретной случайной величины - сумма произведений ее возможных значений на соответствующие им вероятности:
М(Х) =х1р1+х2р2+ … +хпрп .
Если число возможных значений случайной величины бесконечно, то 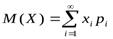 , если полученный ряд сходится абсолютно.
, если полученный ряд сходится абсолютно.
Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.
Замечание 3. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непрерывных случайных величин.
Свойства математического ожидания.
1. Математическое ожидание постоянной равно самой постоянной:
М(С) =С.
- Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) =С М(Х).
- Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M(XY) =M(X)M(Y). - Математическое ожидание суммы двух случайных величин (зависимых или независимых ) равно сумме математических ожиданий слагаемых:
M(X + Y) =M(X) +M(Y).
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
D(X) =M(X – M(X))²
или
D(X) =M(X ²) –M ²(X)
Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида
| Х | 49 | 50 | 51 |
| р | 0,1 | 0,8 | 0,1 |
| Y | 0 | 100 |
| p | 0,5 | 0,5 |
Найдем
М(Х) = 49·0,1 + 50·0,8 + 51·0,1 = 50,
М(Y) = 0·0,5 + 100·0,5 = 50.
Как видно, математические ожидания обеих величин равны, но если для Х М(Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (причем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят отМ(Y).
Следовательно, наряду с математическим ожиданием желательно знать, на сколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.
Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:
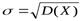 .
.
13. Законы распределения дискретных и непрерывных случайных величин. Плотность вероятности и функция распределения непрерывной случайной величины, связь между ними.
14. Закон Гаусса (закон нормального распределения). Правило 3-х сигм. Применение закона Гаусса в медико-биологических исследованиях. Критерий Пирсона.
Непрерывная случайная величина называется распределенной по нормальному закону (закону Гаусса), если ее плотность вероятности имеет вид
 , (9)
, (9)
где 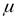 —математическое ожидание;
—математическое ожидание;
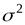 — дисперсия;
— дисперсия;
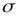 — среднее квадратическое отклонение этой величины.
— среднее квадратическое отклонение этой величины.
График плотности вероятности нормального закона распределения (кривая Гаусса)
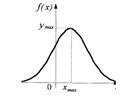 Этот график симметричен относительно вертикальной прямой
Этот график симметричен относительно вертикальной прямой  причем в точке
причем в точке 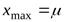 функция имеет максимум, равный
функция имеет максимум, равный 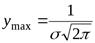 .
.
Правило 3х сигм: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ.
Критерий Пирсона.
Обычно эмпирические и теоретические частоты различаются. Случайно ли расхождение частот? Критерий Пирсона дает ответ на этот вопрос, правда, как и любой статистический критерий, он не доказывает справедливость гипотезы в строго математическом смысле, а лишь устанавливает на определенном уровне значимости ее согласие или несогласие с данными наблюдений.
Итак, пусть по выборке объема  получено статистическое распределение значений признака
получено статистическое распределение значений признака 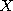 , где
, где 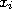 — наблюдаемые значения признака,
— наблюдаемые значения признака, 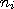 — соответствующие им частоты:
— соответствующие им частоты:
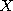
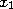
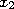
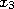 . . .
. . . 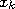

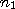
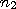
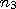 . . .
. . . 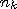
Суть критерия Пирсона состоит в вычислении критерия 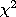 по следующей формуле:
по следующей формуле:
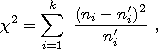
где 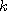 — это число разрядов наблюдаемых значений, а
— это число разрядов наблюдаемых значений, а  — теоретические частоты соответствующих значений.
— теоретические частоты соответствующих значений.
Понятно, что чем меньше разности 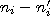 , тем ближе эмпирическое распределение к эмпирическому, поэтому, чем меньше значение критерия
, тем ближе эмпирическое распределение к эмпирическому, поэтому, чем меньше значение критерия 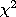 , тем с большей достоверностью можно утверждать, что эмпирическое и теоретическое распределение подчинены одному закону.
, тем с большей достоверностью можно утверждать, что эмпирическое и теоретическое распределение подчинены одному закону.
Алгоритм критерия Пирсона несложен и состоит в выполнении следующих действий:
1. Сначала по данным выборки получают статистическое распределение наблюдаемого признака.
2. Затем — вычисляют теоретические частоты признака, какими они должны были бы быть, если бы признак был действительно распределен в соответствии с данным законом.
3. По данной выше формуле вычисляют эмпирическое значение критерия 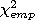
4. По таблице критических значений критерия Пирсона определяют 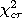 на необходимом уровне значимости
на необходимом уровне значимости  и при заданном числе степеней свободы
и при заданном числе степеней свободы  . Число степеней свободы вычисляется по формуле
. Число степеней свободы вычисляется по формуле 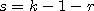 , где
, где 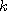 — число разрядов наблюдаемых значений,
— число разрядов наблюдаемых значений,  — число параметров предполагаемого распределения, в случае нормального или равномерного распределения
— число параметров предполагаемого распределения, в случае нормального или равномерного распределения 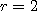 .
.
5. В случае, если 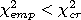 , основную гипотезу принимают, в этом случае на заданном уровне значимости можно утверждать, что статистическое распределение изучаемого параметра подчинено данному закону распределения. Если же имеет место обратное неравенство
, основную гипотезу принимают, в этом случае на заданном уровне значимости можно утверждать, что статистическое распределение изучаемого параметра подчинено данному закону распределения. Если же имеет место обратное неравенство 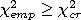 , принимают альтернативную гипотезу: статистическое распределение отличается от данного.
, принимают альтернативную гипотезу: статистическое распределение отличается от данного.
Итак, единственным нетривиальным действием в этом алгоритме является определение теоретических частот.
15. Понятие вариационных рядов и статистического распределения. Основные характеристики вариационного ряда (характеристики положения и характеристики рассеяния).
16. Понятие генеральной совокупности и выборки, характеристики: среднее выборочное, среднее квадратическое отклонение выборочное, дисперсия 2 выборочное.Точечная и интервальная оценка генеральной совокупности. Основные требования к точечной оценке. Уровень значимости и доверительная вероятность.
17. Функциональная и корреляционная зависимости. Понятия прямой и обратной, линейной и нелинейной, сильной и слабой зависимостей.
18. Корреляционный и регрессионный анализ. Коэффициент корреляции, допустимые значения коэффициента корреляции. Корреляционное поле. Уравнение регрессии.
Механические колебания и волны. Акустика.
Решение уравнения:
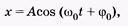 А-амплитуда колебаний;
А-амплитуда колебаний;
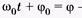 ω— фаза колебаний, φ0 — начальная фаза колебаний (при t = 0); ω0 — круговая частота колебаний.
ω— фаза колебаний, φ0 — начальная фаза колебаний (при t = 0); ω0 — круговая частота колебаний.
Затухающие колебания - колебания, энергия которых уменьшается с течением времени.
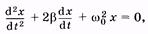 где β- коэффициент затухания, ω0 – круговая частота собственных колебаний системы (без затухания).
где β- коэффициент затухания, ω0 – круговая частота собственных колебаний системы (без затухания).
Резонанс - достижение максимальной амплитуды вынужденных колебаний для заданных β и ω0.
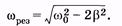 - частота вынужденных колебаний при резонансе.
- частота вынужденных колебаний при резонансе.
 - амплитуда при резонансе.
- амплитуда при резонансе.
Уравнение Ньютона.
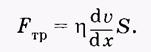 , где h — коэффициент пропорциональности, называемый коэффициентом внутреннего трения, или динамической вязкостью (или просто вязкостью).
, где h — коэффициент пропорциональности, называемый коэффициентом внутреннего трения, или динамической вязкостью (или просто вязкостью).
Так как разделение на слои условно, то принято выражать силу в зависимости от изменения скорости на некотором участке в направлении х, перпендикулярном скорости, отнесенного к длине этого участка, т. е. от величины du/dx — градиента скорости (скорости сдвига).
Единицей вязкости является паскаль-секунда (Па • с).
Для многих жидкостей вязкость не зависит от градиента скорости, такие жидкости подчиняются уравнению Ньютона, и их называют ньютоновскими.
Жидкости, не подчиняющиеся уравнению относят к неньютоновским.
Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютоновских —аномальной.
Реологические свойства крови, плазмы, сыворотки
Жидкости, состоящие из сложных и крупных молекул, например растворы полимеров, и образующие благодаря сцеплению молекул или частиц пространственные структуры, являются неньютоновскими. Их вязкость при прочих равных условиях много больше, чем у простых жидкостей. Увеличение вязкости происходит потому, что при течении этих жидкостей работа внешней силы затрачивается не только на преодоление истинной, ньютоновской, вязкости, но и на разрушение структуры.
Вязкость биожидкостей определяется их структурной частью. Например, вязкость цитоплазмы определяется структурой входящих в ее состав биополимеров. Микровязкость цитоплазмы изменяется в 23 раза и зависит от периодов клеточного цикла. Кроме того, микровязкость различна, в различных частях клетки, и увеличивается при T>40-500С и уменьшается при T<12-150С.
Кровь – это неньютоновская жидкость, т.к. является сложной суспензией белков и клеток крови и представляет собой структурированное полимерное соединение.
Вязкость крови и ее гидродинамические свойства, зависят от концентрации и состава белков, а также от скорости сдвига. Также изменения вязкости объясняются образованием и разрушением столбиков эритроцитов крови.
Формула Пуазейля.
 , где
, где
Q - объем жидкости, протекающей через трубу
η - вязкость жидкости
R - радиус трубы
p - давление
l - длина трубы
29. Методы определения вязкости жидкости: капиллярные, ротационные, закон Стокса. Диагностическое значение определения вязкости крови (вискозиметр Гесса).
Совокупность методов измерения вязкости называют вискозиметрией, и приборы, используемые для таких целей - вискозиметрами.
1. Капиллярные методы основаны на законе Пуазейля и заключаются в измерении времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений.
Вискозиметр Оствальда.
С помощью вискозиметра Оствальда определяют вязкость исследуемой жидкости относительным методом. Измеряют время истечения определенного объема между двумя метками
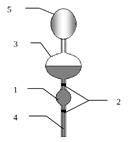

Вискозиметр ВК-4 (вискозиметр Гесса)
Так как вискозиметр Оствальда требует много исследуемой жидкости, то его, как правило, не используют в клинике. В клинической практике для определения вязкости крови используют вискозиметр ВК-4.
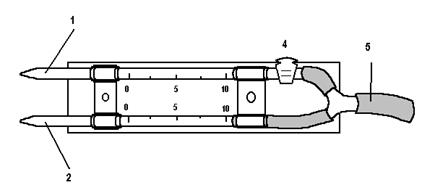 .
.
1 и 2 – градуированные пипетки, 3 – подставка, 4 – кран, 5 – резиновая трубка, через которую отсасывают воздух из прибора.
Путь, пройденный жидкостью в капиллярах одинакового сечения при одинаковых давлениях и температурах, обратно пропорционален внутреннему трению или вязкости:
 . (23)
. (23)
В качестве жидкости сравнения (h0, l0) обычно используют дистиллированную воду. Измерив пути l0и lкр, пройденные дистиллированной водой и кровью, и зная вязкость h0 дистиллированной воды, находят вязкость hкр крови.
2. Метод падающего шарика (метод Стокса).
Метод основан на измерении скорости падения маленьких шариков в исследуемой жидкости
На падающий шарик радиусом r из вещества с плотностью r в вязкой жидкости с плотностью r0 и вязкостью h действуют силы:
- сила тяжести
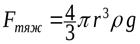 ,
,
- выталкивающая сила
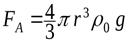 ,
, - сила сопротивления жидкости, которая, согласно закону Стокса, равна FB=6 p r h V, где V- скорость шарика.
Метод применяется при изучении оседания взвешенных частиц (крахмальных зерен, порошка какао и т. п.).
3. Ротационные методы. Измерение вязкости ротационным вискозиметром основано на определении скорости вращения цилиндра в вязкой жидкости.
30. Поверхностное натяжение. Коэффициент поверхностного натяжения. Явление смачиваемости и несмачиваемости. Капиллярные явления. Поверхностно- активные вещества. Газовая эмболия.
31. Ламинарное и турбулентное течение жидкости. Факторы, определяющие характер течения. Число Рейнольдса.
Ламинарное и турбулентное течение жидкости
Течение возможно с перемешивание слоев и без перемешивания.
Течение жидкости с перемешиванием слоем – турбулентное.
Движение жидкости параллельными слоями, не перемешивающимися друг с другом – ламинарное.
Трение при турбулентном движении намного больше, чем при ламинарном, т.к при завихрениях молекулы жидкости проходят значительно больший путь и следовательно взаимодействуют с большим числом молекул, в результате этого при турбулентном движении, энергии на движении расходуется больше.
Характер движения определяется числом Рейнольдса.
Re=ρυD/η, где
ρ-плотность жидкости;
υ-скорость течения в трубе;
D-диаметр трубы;
η-вязкость жидкости в трубе.
Reкрит = 2300 – для воды
Если Re > Reкрит - движение турбулентное
Если Re < Reкрит - движение ламинарное
32. Условие неразрывности струи. Скорость кровотока в разных участках сосудистого русла. Уравнение Бернулли.
P1+ρgh1+ρυ12/2=const – уравнение Бернулли, где
Р – статическое давление; возникает при разности давлении на входе и выходе трубы
ρgh – гидростатическое давление; появляется при подъеме жидкости на высоту
ρυ2/2 – гидродинамическое давление; появляется, когда есть скорость течения жидкости
33. Модели кровообращения (механическая, электрическая). Ограничения представленных моделей. Работа и мощность сердца. Общая энергия массы движущейся крови.
34. Физические основы клинического метода определения давления крови (метод Короткова).
Основы электродинамики. Элементы медицинской электроники.
35. Электрическое поле, его характеристики: напряженность, электрический потенциал. Эквипотенциальные поверхности.
Электрическим полем называют вид материи, посредством которой происходит взаимодействие электрических зарядов. Поле неподвижных зарядов называется электростатическим.
Свойства электрического поля:
• порождается электрическим зарядом;
• обнаруживается по действию на заряд;
• действует на заряды с некоторой силой.
1. силовая характеристика – напряженность (Е) – это векторная физическая величина, численно равная отношению силы, действующей на заряд, помещенный в данную точку поля, к величине этого заряда: Е = F/q; [E] = [ 1 Н/Кл ] = [1 В/м ]
Графически электрическое поле изображают с помощью силовых линий –это линии, касательные к которым в каждой точке пространства совпадают с направлением вектора напряженности.
Силовые линии электрического поля незамкнуты, они начинаются на положительных зарядах и заканчиваются на отрицательных:
2. энергетическая характеристика – потенциал (j) - это скалярная физическая величина, равная отношению потенциальной энергии заряда, необходимой для его перемещения из одной точки поля в другую, к величине этого заряда: j = DЕр/q. [j] = [1 Дж/Кл ] =[1 В ].
Dj = j2 - j1 – изменение потенциала;
U = j1 - j2 - разность потенциалов (напряжение)
36. Физические основы электрокардиографии. Дипольный момент сердца. Теория В.Эйнтховена. Генез зубцов, сегментов и интервалов. Векторкардиография.
Электрический диполь – система двух разноименных по знаку и одинаковых по величине точечных зарядов, находящихся на небольшом расстоянии один от другого. Вектор l, проведенный от отрицательного заряда к положительному, называется плечом диполя. Вектор
p = q*l называется электрическим моментом диполя.
37. Гальванизация, лекарственный электрофорез. Плотность тока в растворе электролитов. Электропроводимость биологических тканей. Первичные процессы, происходящие при действии постоянного тока.
38. Переменный электрический ток и его характеристики. Полное сопротивление в цепи переменного тока. Активное, ёмкостное сопротивление. Понятие импеданса.
39. Эквивалентная электрическая схема тканей организма при воздействии переменным током. Частотная зависимость импеданса (дисперсия импеданса). Физические основы реографии.
40. Электрический импульс и импульсный ток, их характеристики. Применение импульсных токов в медицине.
41. Физические основы применения переменных магнитных (индуктотермия) и электрических (УВЧ-терапия) полей в медицине. Физиотерапевтические методы СВЧ- и микроволновой терапии.
42. Датчики как устройство съема биологических сигналов. Генераторные и параметрические датчики, их классификация и характеристики (функция преобразования, чувствительность, порог чувствительности, предел преобразования).
43. Классификация медицинской электронной аппаратуры. Требования, предъявляемые к медицинской аппаратуре. Понятие электробезопасности и надежности медицинской аппаратуры.
44. Физические основы магнитно-резонансной томографии, компьютерной томографии. Метод ядерного магнитного резонанса.
Оптика. Тепловое излучение тел.
45. Оптическая микроскопия. Предел разрешения, разрешающая способность и связь между ними, полезное увеличение микроскопа. Микроскопия в проходящем и отраженном свете.
46. Специальные методы оптической микроскопии: иммерсионная и ультрафиолетовая микроскопия. Измерение размеров малых объектов. Метод фазового контраста.
47. Поляризованный свет, его отличия от естественного. Способы получения поляризованного света. Понятие поляризатора и анализатора. Закон Малюса. Области применения поляризованного света в медико-биологических исследованиях. Оптически активные вещества формула для определения угла вращения для растворов.
48. Когерентные источники. Интерференция света. Условие максимума и минимума интерференции. Применение интерференции в медицине.
49. Интерференция света в тонких пластинках (пленках). Просветление оптики.
50. Дифракция света. Принцип Гюйгенса–Френеля. Дифракционная решетка. Основная формула дифракционной решетки. Применение дифракции в медико- биологических исследованиях.
51. Оптическая система глаза: светопроводящий и световоспринимающий аппарат. Аккомодация. Острота зрения. Недостатки оптической системы глаза и их компенсация.
52. Линза. Оптическая сила линзы. Построение изображений в линзах. Формула тонкой линзы. Аберрации линз: сферическая, хроматическая, астигматизм.
53. Законы отражения и преломления света. Полное внутреннее отражение. Волоконная оптика и ее использование в медицине.
54. Ультрафиолетовое (УФ) излучение. Основные характеристики и источники. Фотобиологические процессы возникающие при УФ-облучении. Использование УФ-света в медицине.
55. Основные характеристики инфракрасного (теплового) излучения: спектральная плотность энергетической светимости, коэффициент поглощения. Черное и серое тела. Закон Кирхгофа.
56. Энергетическая светимость черного тела. Законы Стефана–Больцмана и смещения Вина.
57. Применение теплового излучения в медицине. Тепловое излучение человека. Методы термографии и тепловидения.
Рентгеновское излучение. Дозиметрия.
58. Рентгеновское излучение. Основные характеристики рентгеновского излучения. Устройство рентгеновской трубки. Тормозное и характеристическое рентгеновское излучение. Зависимость спектра излучения от напряжения между электродами, температуры накала катода и материала анода.
59. Закон ослабления потока рентгеновского излучения веществом. Механизмы взаимодействие рентгеновского излучения с веществом: фотоэффект, когерентное, некогерентное рассеяние.
60. Физические основы применения рентгеновского излучения в медицине. Рентгенодиагностика. Рентгенотерапия. Компьютерная томография. . g , b , a
61. Радиоактивность. Виды и свойства радиоактивных излучений: -излучения. Основной закон радиоактивного g -, b -, a Энергетические спектры распада. Период полураспада.
62. Биофизические основы действия радиоактивных излучений на организм. Прямое и опосредованное повреждение биомолекул. Защита от ионизирующих излучений.
63. Дозиметрия ионизирующих излучений (поглощенная, экспозиционная, эквивалентная дозы). Мощность дозы. Дозиметрические приборы. Естественный фон и допустимые значения доз ионизирующего излучения.
64. Физические основы применения ионизирующих излучений в медицине: -терапия). Требования a (диагностическое использование радиофармпрепаратов, предъявляемые к радиофармпрепаратам.
Физические процессы в биологических мембранах.
65. Плазматические мембраны, их структура и функции. Физические свойства и параметры биомембран: жидкокристаллическое состояние, толщина, микровязкость, электрическая ёмкость.
66. Пассивный транспорт веществ через плазматические мембраны. Простая диффузия. Уравнения Фика, Нернста-Планка. Особенности транспорта гидрофобных и гидрофильных веществ. Облегченная диффузия.
67. Осмос. Характеристика растворов по величине осмотического давления. Фильтрация.
68. Активный транспорт веществ через плазматические мембраны. Опыт Уиссинга. Первичный активный транспорт. Принцип работы ионных насосов (Na+ -K + -АТФ- аза, Ca2+ -АТФ-аза, Н+ -АТФ-аза). Вторичный активный транспорт.
69. Мембранный потенциал покоя. Мембранно-ионная теория образования потенциала покоя. Уравнение Гольдмана-Ходжкина-Катца. Биологическое значение потенциала покоя.
70. Потенциал действия: механизм образования, свойства. Фазы потенциала действия. Процессы, приводящие к изменению величины мембранного потенциала. Биологическое значение потенциала действия. Изменение возбудимости мембраны во время потенциала действия.
Основные элементарные функции и их графики. Примеры показательной и степенной функции.
Основными элементарными функциями являются
§ постоянная функция (константа),
§ корень n-ой степени, степенная функция,
§ показательная,
§ тригонометрические и обратные тригонометрические функции,
§ логарифмическая функция.
Постоянная. 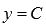

Свойства постоянной функции.
· Область определения: все множество действительных чисел.
· Постоянная функция является четной.
· Область значений: множество, состоящее из единственного числа С.
· Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
· Говорить о выпуклости и вогнутости постоянной не имеет смысла.
· Асимптот нет.
· Функция проходит через точку (0,C) координатной плоскости.
Корень n-ой степени, степенная функция. 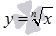
1. n - четное число.

Свойства функции корень n-ой степени при четных n.
· Область определения: множество всех неотрицательных действительных чисел 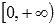 .
.
· При x=0 функция 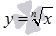 принимает значение, равное нулю.
принимает значение, равное нулю.
· Эта функция общего вида (не является четной или нечетной).
· Область значений функции: 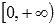 .
.
· Функция 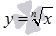 при четных показателях корня возрастает на всей области определения.
при четных показателях корня возрастает на всей области определения.
· Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
· Асимптот нет.
· График функции корень n-ой степени при четных n проходит через точки (0,0) и(1,1).
2. n - нечетное число.

Свойства функции корень n-ой степени при нечетных n.
· Область определения: множество всех действительных чисел.
· Эта функция нечетная.
· Область значений функции: множество всех действительных чисел.
· Функция 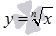 при нечетных показателях корня возрастает на всей области определения.
при нечетных показателях корня возрастает на всей области определения.
· Эта функция вогнутая на промежутке 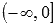 и выпуклая на промежутке
и выпуклая на промежутке 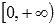 , точка с координатами (0,0) – точка перегиба.
, точка с координатами (0,0) – точка перегиба.
· Асимптот нет.
· График функции корень n-ой степени при нечетных n проходит через точки (-1,-1),(0,0) и (1,1).
Степенная. 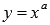
1. а - нечетное число, а>0

Свойства степенной функции с нечетным положительным показателем.
· Область определения:  .
.
· Область значений: 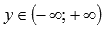 .
.
· Функция нечетная, так как 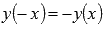 .
.
· Функция возрастает при  .
.
· Функция выпуклая при 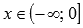 и вогнутая при
и вогнутая при 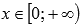 (кроме линейной функции).
(кроме линейной функции).
· Точка (0;0) является точкой перегиба (кроме линейной функции).
· Асимптот нет.
· Функция проходит через точки (-1;-1), (0;0), (1;1).
2. а - четное число, а>0

Свойства степенной функции с четным положительным показателем.
· Область определения:  .
.
· Область значений: 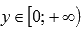 .
.
· Функция четная, так как 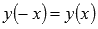 .
.
· Функция возрастает при 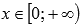 , убывает при
, убывает при 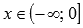 .
.
· Функция вогнутая при  .
.
· Точек перегиба нет.
· Асимптот нет.
· Функция проходит через точки (-1;1), (0;0), (1;1).
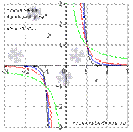
3. а - нечетное число, а<0

Свойства степенной функции с нечетным отрицательным показателем.
· Область определения: 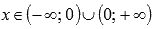 . При x=0 имеем разрыв второго рода, так как
. При x=0 имеем разрыв второго рода, так как 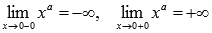 приа=-1,-3,-5,…. Следовательно, прямая x=0 является вертикальной асимптотой.
приа=-1,-3,-5,…. Следовательно, прямая x=0 является вертикальной асимптотой.
· Область значений: 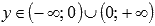 .
.
· Функция нечетная, так как 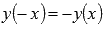 .
.
· Функция убывает при 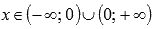 .
.
· Функция выпуклая при 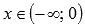 и вогнутая при
и вогнутая при 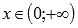 .
.
· Точек перегиба нет.
· Горизонтальной асимптотой является прямая y = 0, так как 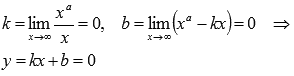 при а=-1,-3,-5,….
при а=-1,-3,-5,….
· Функция проходит через точки (-1;-1), (1;1).
4. а - четное число, а<0

Свойства степенной функции с четным отрицательным показателем.
· Область определения: 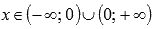 . При x=0 имеем разрыв второго рода, так как
. При x=0 имеем разрыв второго рода, так как 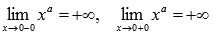 приа=-2,-4,-6,…. Следовательно, прямая x=0 является вертикальной асимптотой.
приа=-2,-4,-6,…. Следовательно, прямая x=0 является вертикальной асимптотой.
· Область значений:  .
.
· Функция четная, так как 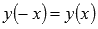 .
.
· Функция возрастает при 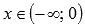 , убывает при
, убывает при 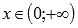 .
.
· Функция вогнутая при 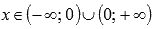 .
.
· Точек перегиба нет.
· Горизонтальной асимптотой является прямая y=0, так как 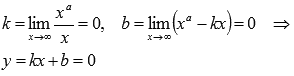 при а=-2,-4,-6,….
при а=-2,-4,-6,….
· Функция проходит через точки (-1;1), (1;1).
Показательная.  , где
, где 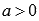 ,
, 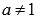 .
.
1. 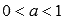

Свойства показательной функции с основанием меньшим единицы.
· Областью определения показательной функции является все множество действительнйх чисел:  .
.
· Область значений:  .
.
· Функция не является ни четной, ни нечетной, то есть, она общего вида.
· Показательная функция, основание которой меньше единицы, убывает на всей области определения.
· Функция вогнутая при  .
.
· Точек перегиба нет.
· Горизонтальной асимптотой является прямая y = 0 при х стремящемся к плюс бесконечности.
· Функция проходит через точку (0;1).
2. 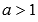

Свойства показательной функции с основанием большим единицы.
· Область определения показательной функции:  .
.
· Область значений:  .
.
· Функция не является ни четной, ни нечетной, то есть она общего вида.
· Показательная функция, основание которой больше единицы, возрастает при  .
.
· Функция вогнутая при  .
.
· Точек перегиба нет.
· Горизонтальной асимптотой является прямая y = 0 при х стремящемся к минус бесконечности.
· Функция проходит через точку (0;1).
Тригонометрические и обратные тригонометрические. 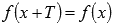
1. Синусоида. y = sin(x)

Свойства функции синус y = sin(x).
· Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при  .
.
· Наименьший положительный период функции синуса равен двум пи: 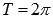 .
.
· Функция обращается в ноль при 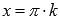 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть 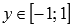 .
.
· Функция синус - нечетная, так как 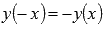 .
.
· Функция убывает при 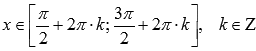 , возрастает при
, возрастает при 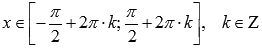 .
.
· Функция синус имеет локальные максимумы в точках 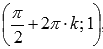 , локальные минимумы в точках
, локальные минимумы в точках 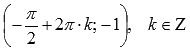 .
.
· Функция y = sinx вогнутая при 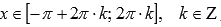 , выпуклая при
, выпуклая при 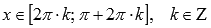 .
.
· Координаты точек перегиба 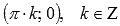 .
.
· Асимптот нет.
2. Косинусоида. y = cos(x)

Свойства функции косинус y = cos(x).
· Область определения функции косинус:  .
.
· Наименьший положительный период функции y = cosx равен двум пи: 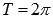 .
.
· Функция обращается в ноль при 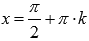 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции косинус представляет интервал от минус единицы до единицы включительно: 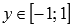 .
.
· Функция косинус - четная, так как 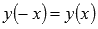 .
.
· Функция убывает при 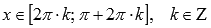 , возрастает при
, возрастает при 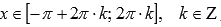 .
.
· Функция y = cosx имеет локальные максимумы в точках 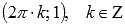 , локальные минимумы в точках
, локальные минимумы в точках 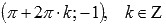 .
.
· Функция вогнутая при 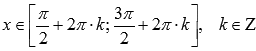 , выпуклая при
, выпуклая при 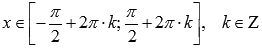 .
.
· Координаты точек перегиба  .
.
· Асимптот нет.
3. Тангенсоида. y = tg(x).

Свойства функции тангенс y = tg(x).
· Область определения функции тангенс: 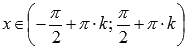 , где
, где  , Z – множество целых чисел. Поведение функции y = tgx на границе области определения
, Z – множество целых чисел. Поведение функции y = tgx на границе области определения 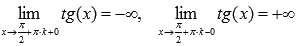 Следовательно, прямые
Следовательно, прямые 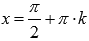 , где
, где  , являются вертикальными асимптотами.
, являются вертикальными асимптотами.
· Наименьший положительный период функции тангенс  .
.
· Функция обращается в ноль при 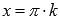 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции y = tg(x): 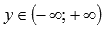 .
.
· Функция тангенс - нечетная, так как 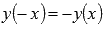 .
.
· Функция возрастает при 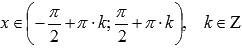 .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при 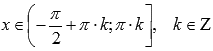 .
.
· Координаты точек перегиба 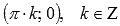 .
.
· Наклонных и горизонтальных асимптот нет.
4. Котангенсоида. y = ctg(x)

Свойства функции котангенс y = ctgx.
· Область определения функции котангенс: 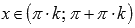 , где
, где  , Z – множество целых чисел. Поведение на границе области определения
, Z – множество целых чисел. Поведение на границе области определения 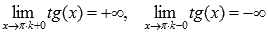 Следовательно, прямые
Следовательно, прямые 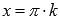 , где
, где  являются вертикальными асимптотами.
являются вертикальными асимптотами.
· Наименьший положительный период функции y = ctgx равен пи:  .
.
· Функция обращается в ноль при 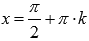 , где
, где  , Z – множество целых чисел.
, Z – множество целых чисел.
· Область значений функции котангенс: 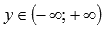 .
.
· Функция нечетная, так как 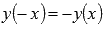 .
.
· Функция y = ctg(x) убывает при 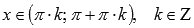 .
.
· Функция котангенс вогнутая при 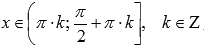 , выпуклая при
, выпуклая при  .
.
· Координаты точек перегиба  .
.
· Наклонных и горизонтальных асимптот нет.
5. Арксинусоида. y = arcsin(x)

Свойства функции арксинус y = arcsin(x).
· Областью определения функции арксинус является интервал от минус единицы до единицы включительно: 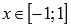 .
.
· Область значений функции y = arcsin(x): 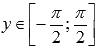 .
.
· Функция арксинус - нечетная, так как 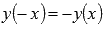 .
.
· Функция y = arcsin(x) возрастает на всей области определения, то есть, при 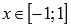 .
.
· Функция вогнутая при 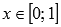 , выпуклая при
, выпуклая при  .
.
· Точка перегиба (0; 0), она же ноль функции.
· Асимптот нет.
6. Арккосинусоида. y = arccos(x)

Свойства функции арккосинус y = arccos(x).
· Область определения функции арккосинус: 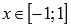 .
.
· Область значений функции y = arccos(x): 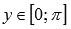 .
.
· Функция не является ни четной ни нечетной, то есть, она общего вида.
· Функция арккосинус убывает на всей области определения, то есть, при 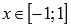 .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при 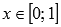 .
.
· Точка перегиба  .
.
· Асимптот нет.
7. Арктангенсоида. y = arctg(x)

Свойства функции арктангенс y = arctg(x).
· Область определения функции y = arctg(x):  .
.
· Область значений функции арктангенс: 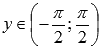 .
.
· Функция арктангенс - нечетная, так как 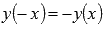 .
.
· Функция возрастает на всей области определения, то есть, при  .
.
· Функция арктангенс вогнутая при 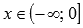 , выпуклая при
, выпуклая при 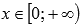 .
.
· Точка перегиба (0; 0), она же ноль функции.
· Горизонтальными асимптотами являются прямые  при
при 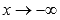 и
и 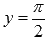 при
при 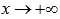 . На чертеже они показаны зеленым цветом.
. На чертеже они показаны зеленым цветом.
8. Арккотангенсоида. y = arcctg(x)

Свойства функции арккотангенс y = arcctg(x).
· Областью определения функции арккотангенс является все множество действительных чисел:  .
.
· Область значений функции y = arcctg(x): 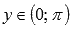 .
.
· Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
· Функция убывает на всей области определения, то есть, при  .
.
· Функция вогнутая при 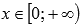 , выпуклая при
, выпуклая при 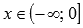 .
.
· Точка перегиба  .
.
· Горизонтальными асимптотами являются прямые 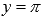 при
при 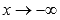 (на чертеже показана зеленым цветом) и y = 0 при
(на чертеже показана зеленым цветом) и y = 0 при 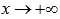 .
.
Логарифмическая  , где
, где 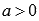 ,
, 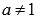 .
. 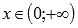
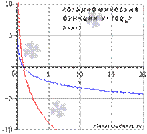
1. 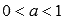

Свойства логарифмической функции с основанием меньшим единицы.
· Область определения логарифмической функции: 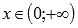 . При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности.
. При х стремящемся к нулю справа, значения функции стремятся к плюс бесконечности.
· Область значений: 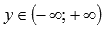 .
.
· Функция не является ни четной, ни нечетной, то есть она общего вида.
· Логарифмическая функция убывает на всей области определения.
· Функция вогнутая при 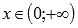 .
.
· Точек перегиба нет.
· Горизонтальных асимптот нет.
· Функция проходит через точку (1;0).
2. 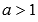

Свойства логарифмической функции с основанием большим единицы.
· Область определения: 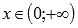 . При х стремящемся к нулю справа, значения функции стремятся к минус бесконечности.
. При х стремящемся к нулю справа, значения функции стремятся к минус бесконечности.
· Областю значений логарифмической функции является все множество действительных чисел, то есть, интервал 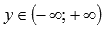 .
.
· Функция не является ни четной, ни нечетной, то есть она общего вида.
· Функция возрастает при 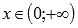 .
.
· Функция выпуклая при 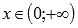 .
.
· Точек перегиба нет.
· Горизонтальных асимптот нет.
· Функция проходит через точку (1;0).
2. Предел функции. Основные теоремы о пределах. Методы раскрытия неопределенностей. Использования правила Лопиталя.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.
Теоремы о пределах.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
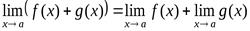
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
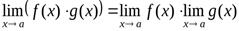 .
.
Следствие 1 . Постоянный множитель можно выносить за знак предела:
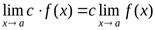 .
.
Следствие 2 . Предел степени равен степени предела:
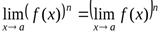 .
.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
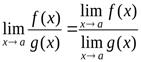 , если
, если 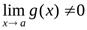 .
.
Методы раскрытия неопределенностей.
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.
1. Разложение числителя и знаменателя на множители с последующим сокращением
2. Деление многочлена на многочлен
3. Устранение иррациональных разностей домножением на сопряженное выражение
4. Замена переменной
5. Первый замечательный предел
6. Правило Лопиталя
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа 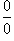 или
или  . Пусть a является некоторым конечным действительным числом или равно бесконечности.
. Пусть a является некоторым конечным действительным числом или равно бесконечности.
· Если 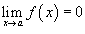 и
и 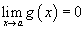 , то
, то 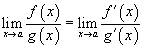 ;
;
· Если 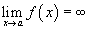 и
и 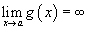 , то аналогично
, то аналогично 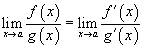 .
.
Правило Лопиталя можно также применять к неопределенностям типа  . Первые две неопределенности
. Первые две неопределенности 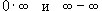 можно свести к типу
можно свести к типу 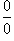 или
или  с помощью алгебраических преобразований. А неопределенности
с помощью алгебраических преобразований. А неопределенности 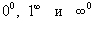 сводятся к типу
сводятся к типу 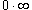 с помощью соотношения
с помощью соотношения
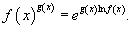
Правило Лопиталя справедливо также и для односторонних пределов.
3. Понятие производной. Геометрический и физический смысл производной.
Произво́дная функции в точке — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
1. Физический смысл производной.
Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная 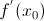 – скорость изменения переменной y относительно переменной x в точке
– скорость изменения переменной y относительно переменной x в точке 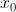 .
.
Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная 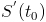 – скорость в момент времени
– скорость в момент времени 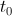 .
.
Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то 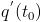 – скорость изменения количества электричества в момент времени
– скорость изменения количества электричества в момент времени 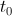 , т.е. сила тока в момент времени
, т.е. сила тока в момент времени 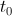 .
.
2. Геометрический смысл производной.
Пусть 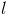 – некоторая кривая,
– некоторая кривая,  – точка на кривой
– точка на кривой 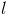 .
.
Любая прямая, пересекающая 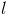 не менее чем в двух точках называется секущей.
не менее чем в двух точках называется секущей.
Касательной к кривой 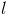 в точке
в точке 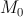 называется предельное положение секущей
называется предельное положение секущей 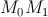 , если точка
, если точка 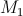 стремится к
стремится к 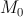 , двигаясь по кривой.
, двигаясь по кривой.
Если касательная к кривой в точке 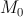 существует, то она единственная.
существует, то она единственная.
4. Применение пределов для нахождения производных элементарных функций. Производные основных элементарных функций.
5. Основные правила дифференцирования. Дифференцирование сложной функции. Привести пример.
Теорема 1. Если функции  и
и 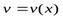 дифференцируемы в данной точке, то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых:
дифференцируемы в данной точке, то в той же точке дифференцируема и их сумма, причем производная суммы равна сумме производных слагаемых:
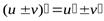 .
.
Формула обобщается на случай любого конечного числа слагаемых.
Теорема 2. Если функции 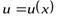 и
и 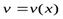 дифференцируемы в данной точке х, то в этой же точке дифференцируемо и их произведение, при этом:
дифференцируемы в данной точке х, то в этой же точке дифференцируемо и их произведение, при этом:
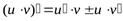 .
.
Следствие. Постоянный множитель можно выносить за знак производной:
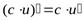 , где
, где 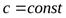 .
.
Теорема 3. Если в данной точке х функции 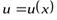 и
и 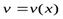 дифференцируемы и
дифференцируемы и 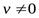 , то в той же точке дифференцируемо и их частное, причем
, то в той же точке дифференцируемо и их частное, причем
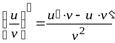 .
.
Производная сложной функции.
Если 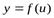 и
и 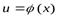 , то
, то 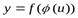 есть сложная функция независимого аргумента x с промежуточным аргументом u.
есть сложная функция независимого аргумента x с промежуточным аргументом u.
Теорема. Если 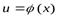 имеет производную
имеет производную  в точке x, а функция
в точке x, а функция 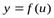 имеет производную
имеет производную 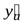 в соответствующей точке u, то сложная функция
в соответствующей точке u, то сложная функция  в данной точке x имеет производную
в данной точке x имеет производную 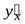 , которая находится по следующей формуле
, которая находится по следующей формуле 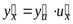 .
.
Часто пользуются следующей формулировкой этой теоремы: производная сложной функции равна произведению производной внешней функции по промежуточному аргументу на производную внутренней функции по независимому аргументу.
Сложная функция может быть составлена не из двух функций, а из большого их числа. В таких случаях теорема применяется последовательно несколько раз.
В частности, если функция 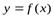 такова, что
такова, что 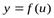 ,
, 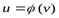 ,
, 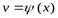 , то производная
, то производная  находится по формуле
находится по формуле 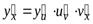 .
.
Пример:
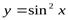 . Здесь у = u2; u=sin x. Тогда
. Здесь у = u2; u=sin x. Тогда
 .
.
6. Понятие первообразной функции и неопределенного интеграла, свойства. Графическое изображение.
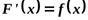
Функция  называется первообразной функцией для функции
называется первообразной функцией для функции  на интервале
на интервале 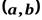 , если
, если 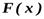 дифференцируема на интервале
дифференцируема на интервале  и
и 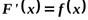 .
.
Если функция имеет первообразную, то она имеет бесконечное множество первообразных.
Произвольная первообразная для 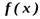 на
на  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 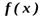 и обозначается символом
и обозначается символом

Знак 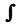 называется интегралом,
называется интегралом,
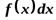 - подынтегральное выражение,
- подынтегральное выражение,
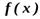 - подынтегральная функция.
- подынтегральная функция.
Таким образом, если 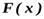 одна из первообразных для
одна из первообразных для  , то
, то


Свойства неопределенного интеграла:
1. 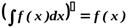
2. 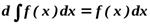
3. 
4. 
7. Нахождение первообразной функции. Пример. Простейшие методы интегрирования.
Операцию нахождения неопределенного интеграла называют интегрированием функции 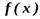 . Она противоположна операции дифференцирования.
. Она противоположна операции дифференцирования.
Пример.
Найти 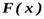 , если
, если 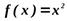 .
.
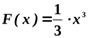 ;
; 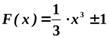 ; и т.д.
; и т.д.
В общем случае  .
.
Или
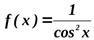
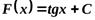 . Или
. Или 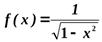
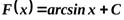
Простейшие способы интегрирования.
а) Непосредственное интегрирование.
Нахождение интегралов функций, основанное на прямом применении свойств неопределенных интегралов и таблицы основных формул интегрирования.
Пример:
∫(х–3)2dх= ∫(х2–6х+9)dх= ∫х2dх- 6∫хdх+9∫dх= х3∕3 -3 х2+9х+С.
б) Интегрирование подстановкой (замена переменной).
Интегрирование подстановкой, или как его часто называют, методом замены переменой, является одним из более эффективных и распространенных методов интегрирования.
Способ подстановки состоит в том, чтобы перейти от данной переменной интегрирования к другой переменной с целью упростить подынтегральное выражение и привести его к одному из табличных видов интегралов.
При этом выбор подстановки решается исполнителем индивидуально, т.к. не существует общих правил, указывающих какую подстановку в данном случае взять.
Пример:
Найти интеграл ∫е2х+3dх.
Введем новую переменную t, связанную с х следующей зависимостью 2х+3=t.
Возьмем дифференциалы от левой и правой частей этого равенства: 2dх=dt;dх=dt/2.
Теперь вместо 2х+3иdх в подинтегральное выражение подставим их значения. Тогда получим: ∫е2х+3dх=  ∫еtdt=
∫еtdt=  еt + С. Возвращаясь к прежней переменной, получим окончательно выражение:
еt + С. Возвращаясь к прежней переменной, получим окончательно выражение:
∫е2х+3dх=  е2х+3 + С.
е2х+3 + С.
8. Понятие определенного интеграла, свойства. Геометрический смысл определенного интеграла. Формула Ньютона – Лейбница.
Пусть функция 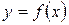 определена на
определена на 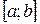 .
.
Разобьём 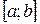 произвольным образом точками
произвольным образом точками 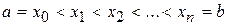 на
на  частичных отрезков длиной
частичных отрезков длиной 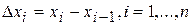 . Выберем в каждом из них произвольно точку
. Выберем в каждом из них произвольно точку 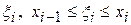 и найдем значения функции в каждой из этих точек
и найдем значения функции в каждой из этих точек 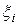 , то есть
, то есть  .
.
Сумма вида
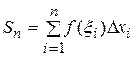 (5.1)
(5.1)
называется n-ой интегральной суммой функции 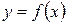 на
на 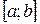 .
.

Геометрический смысл интегральной суммы – сумма площадей прямоугольников с основаниями 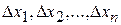 и высотами
и высотами 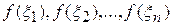 .
.
Обозначим через 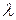 длину наибольшего частичного отрезка данного разбиения
длину наибольшего частичного отрезка данного разбиения 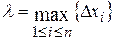 . Найдем предел интегральной суммы
. Найдем предел интегральной суммы  , когда
, когда 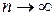 так, что
так, что 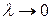 .
.
Если существует конечный предел 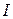 суммы (5.1), не зависящий от способа разбиения отрезка
суммы (5.1), не зависящий от способа разбиения отрезка 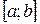 на частичные отрезки и выбора в них точек
на частичные отрезки и выбора в них точек 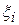 , то этот предел называется определённым интегралом от функции
, то этот предел называется определённым интегралом от функции 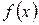 по отрезку
по отрезку 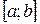 и обозначается:
и обозначается: 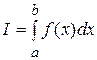 .
.
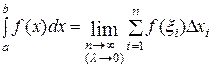
,
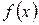 – подынтегральная функция,
– подынтегральная функция,
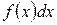 – подынтегральное выражение,
– подынтегральное выражение,
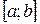 – отрезок интегрирования,
– отрезок интегрирования,
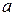 и
и 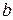 – нижний и верхний пределы интегрирования,
– нижний и верхний пределы интегрирования,
 – переменная интегрирования.
– переменная интегрирования.
Свойства.
1) Если переставить пределы интегрирования, то изменится лишь знак:
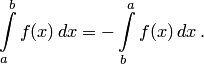
2) Каковы бы ни были а и b, всегда имеет место равенство:

3) Постоянный множитель А выносится за знак определенного интеграла:
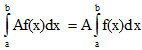
4) Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций:
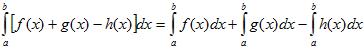
5) Если f(x) – неотрицательная на [a;b], функция и нижний предел меньше верхнего предела (a<b), то и сам интеграл – число неотрицательное, т.е.:
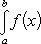

Замечание: если f(x) ≤0 на [a;b] и a<b, то 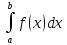 ≤0
≤0
Если f(x) ≥0 на [a;b] и a>b имеем 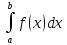 ≤0
≤0
Если f(x) ≤0 на [a;b], то 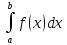 ≥0
≥0
6) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то:
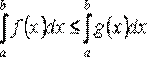 , т.е. неравенство почленно интегрируется.
, т.е. неравенство почленно интегрируется.
7) Если a ≤ b и f(x) непрерывна на [a, b], то:
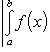
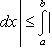
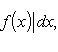 , т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.
, т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.
8) Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a;b], то:
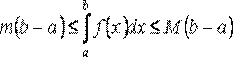
9) Теорема о среднем:
Если функция f(x) непрерывна на [a;b], то существует хотя бы одна точка С на этом отрезке, такая, что справедливо равенство:
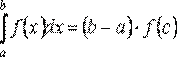
Замечание: формула справедлива также для a>b, кроме a<b
Если a>b, то:
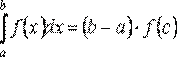 , (b=<c=<a)
, (b=<c=<a)
Геометрический смысл:
Если f(x) >=0 на отрезке [a;b], то интеграл левой части есть площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), а правая часть – площадь прямоугольника с тем же основанием и h=f(c). Для площади криволинейной трапеции всегда есть равновеликий ей прямоугольник с тем же основанием и h, равной ординате этой кривой.
10) Определенный интеграл с одинаковыми пределами равен 0.
 =0
=0
Формула Ньютона - Лейбница
Если f(x) непрерывна на отрезке [a;b], и F(x) - некоторая первообразная функции f(x), То:
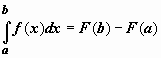
Формулу Ньютона-Лейбница обычно записывают так:
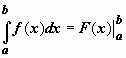
9. Основные определения теории обыкновенных дифференциальных уравнений. Применение дифференциального исчисления для решения прикладных задач биологии и медицины.
10. Случайные события и их классификация. Понятие непрерывной и дискретной случайной величины.
Случайной величиной называется переменная величина, значение которой зависит от исхода некоторого испытания.
Дискретной называется случайная величина, которая может принимать значения некоторой конечной или бесконечной числовой последовательности (число таблеток в упаковке, больных в палате, студентов в аудитории ...).
Непрерывной называется случайная величина, которая может принимать любые значения внутри некоторого интервала (масса, температура, рост ..).
11. Основные положения теории вероятности. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула полной вероятности.
12. Характеристики случайных величин: (математическое ожидание, дисперсия, среднее квадратическое отклонение).
Математическое ожидание дискретной случайной величины - сумма произведений ее возможных значений на соответствующие им вероятности:
М(Х) =х1р1+х2р2+ … +хпрп .
Если число возможных значений случайной величины бесконечно, то 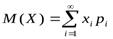 , если полученный ряд сходится абсолютно.
, если полученный ряд сходится абсолютно.
Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.
Замечание 3. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непрерывных случайных величин.
Свойства математического ожидания.
1. Математическое ожидание постоянной равно самой постоянной:
М(С) =С.
- Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) =С М(Х).
- Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M(XY) =M(X)M(Y). - Математическое ожидание суммы двух случайных величин (зависимых или независимых ) равно сумме математических ожиданий слагаемых:
M(X + Y) =M(X) +M(Y).
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
D(X) =M(X – M(X))²
или
D(X) =M(X ²) –M ²(X)
Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида
| Х | 49 | 50 | 51 |
| р | 0,1 | 0,8 | 0,1 |
| Y | 0 | 100 |
| p | 0,5 | 0,5 |
Найдем
М(Х) = 49·0,1 + 50·0,8 + 51·0,1 = 50,
М(Y) = 0·0,5 + 100·0,5 = 50.
Как видно, математические ожидания обеих величин равны, но если для Х М(Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (причем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят отМ(Y).
Следовательно, наряду с математическим ожиданием желательно знать, на сколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.
Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:
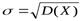 .
.
13. Законы распределения дискретных и непрерывных случайных величин. Плотность вероятности и функция распределения непрерывной случайной величины, связь между ними.
14. Закон Гаусса (закон нормального распределения). Правило 3-х сигм. Применение закона Гаусса в медико-биологических исследованиях. Критерий Пирсона.
Непрерывная случайная величина называется распределенной по нормальному закону (закону Гаусса), если ее плотность вероятности имеет вид
 , (9)
, (9)
где  —математическое ожидание;
—математическое ожидание;
 — дисперсия;
— дисперсия;
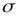 — среднее квадратическое отклонение этой величины.
— среднее квадратическое отклонение этой величины.
График плотности вероятности нормального закона распределения (кривая Гаусса)
 Этот график симметричен относительно вертикальной прямой
Этот график симметричен относительно вертикальной прямой  причем в точке
причем в точке 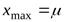 функция имеет максимум, равный
функция имеет максимум, равный 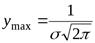 .
.
Правило 3х сигм: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ.
Критерий Пирсона.
Обычно эмпирические и теоретические частоты различаются. Случайно ли расхождение частот? Критерий Пирсона дает ответ на этот вопрос, правда, как и любой статистический критерий, он не доказывает справедливость гипотезы в строго математическом смысле, а лишь устанавливает на определенном уровне значимости ее согласие или несогласие с данными наблюдений.
Итак, пусть по выборке объема  получено статистическое распределение значений признака
получено статистическое распределение значений признака 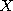 , где
, где 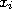 — наблюдаемые значения признака,
— наблюдаемые значения признака, 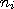 — соответствующие им частоты:
— соответствующие им частоты:
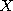
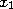
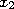
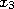 . . .
. . . 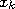

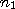
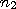
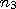 . . .
. . . 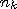
Суть критерия Пирсона состоит в вычислении критерия 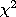 по следующей формуле:
по следующей формуле:
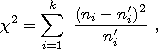
где 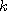 — это число разрядов наблюдаемых значений, а
— это число разрядов наблюдаемых значений, а  — теоретические частоты соответствующих значений.
— теоретические частоты соответствующих значений.
Понятно, что чем меньше разности  , тем ближе эмпирическое распределение к эмпирическому, поэтому, чем меньше значение критерия
, тем ближе эмпирическое распределение к эмпирическому, поэтому, чем меньше значение критерия  , тем с большей достоверностью можно утверждать, что эмпирическое и теоретическое распределение подчинены одному закону.
, тем с большей достоверностью можно утверждать, что эмпирическое и теоретическое распределение подчинены одному закону.
Алгоритм критерия Пирсона несложен и состоит в выполнении следующих действий:
1. Сначала по данным выборки получают статистическое распределение наблюдаемого признака.
2. Затем — вычисляют теоретические частоты признака, какими они должны были бы быть, если бы признак был действительно распределен в соответствии с данным законом.
3. По данной выше формуле вычисляют эмпирическое значение критерия 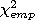
4. По таблице критических значений критерия Пирсона определяют 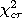 на необходимом уровне значимости
на необходимом уровне значимости  и при заданном числе степеней свободы
и при заданном числе степеней свободы  . Число степеней свободы вычисляется по формуле
. Число степеней свободы вычисляется по формуле 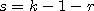 , где
, где 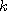 — число разрядов наблюдаемых значений,
— число разрядов наблюдаемых значений,  — число параметров предполагаемого распределения, в случае нормального или равномерного распределения
— число параметров предполагаемого распределения, в случае нормального или равномерного распределения 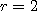 .
.
5. В случае, если 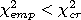 , основную гипотезу принимают, в этом случае на заданном уровне значимости можно утверждать, что статистическое распределение изучаемого параметра подчинено данному закону распределения. Если же имеет место обратное неравенство
, основную гипотезу принимают, в этом случае на заданном уровне значимости можно утверждать, что статистическое распределение изучаемого параметра подчинено данному закону распределения. Если же имеет место обратное неравенство 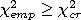 , принимают альтернативную гипотезу: статистическое распределение отличается от данного.
, принимают альтернативную гипотезу: статистическое распределение отличается от данного.
Итак, единственным нетривиальным действием в этом алгоритме является определение теоретических частот.
15. Понятие вариационных рядов и статистического распределения. Основные характеристики вариационного ряда (характеристики положения и характеристики рассеяния).
16. Понятие генеральной совокупности и выборки, характеристики: среднее выборочное, среднее квадратическое отклонение выборочное, дисперсия 2 выборочное.Точечная и интервальная оценка генеральной совокупности. Основные требования к точечной оценке. Уровень значимости и доверительная вероятность.
17. Функциональная и корреляционная зависимости. Понятия прямой и обратной, линейной и нелинейной, сильной и слабой зависимостей.
18. Корреляционный и регрессионный анализ. Коэффициент корреляции, допустимые значения коэффициента корреляции. Корреляционное поле. Уравнение регрессии.
Механические колебания и волны. Акустика.
Дата: 2019-07-24, просмотров: 1621.