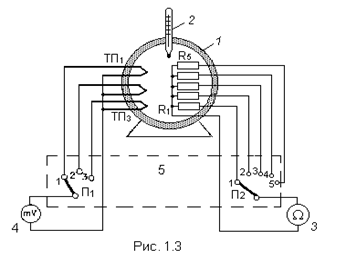
 |
Экспериментальная установка изображена на рис. 1.3. Образцы проволочных резисторов R1–R4, изготовленные из меди, константана, манганина и нихрома, металлопленочный резистор МЛТ-1 (R5) и термопары ТП1–ТП3 помещаются в термостат 1 с термометром 2. Электрическое сопротивление резисторов измеряется омметром 3, э.д.с. термопар – милливольтметром 4. Переключатели П1 и П2 размещены на плате 5 и позволяют поочередно подключать к измерителям исследуемые проводники и термопары. Там же приведена таблица с указанием вида, длины и сечения исследуемых проводников.
Порядок проведения работы
Внимание: все измерения по последующим пунктам проводятся одновременно.
3.1. Определение удельного электрического сопротивления проводников и вычисление aR, ar.
Проводники, помещенные в термостат, поочередно подключить к входным зажимам омметра и замерить их сопротивления сначала при комнатной температуре, а затем при повышении температуры до 90 °С с шагом 10 оС. Результаты измерений записать с максимальной точностью в табл.1.2.
Таблица 1.2
| проводник | q, oС | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| медь | R1 | ||||||||
| r1 | |||||||||
| aR1 | |||||||||
| ar1 | |||||||||
Константан
3.2. Определение зависимости термо-э.д.с термопар от температуры.
Одновременно с нагреванием проводников нагреваются помещенные в термостат спаи трех термопар. Холодные концы термопар поочередно подключить переключателем П1 к милливольтметру. Значения измеренных термо-э.д.с. занести в табл. 1.3.
Таблица 1.3
|
q, °С
| ET, мВ | ||
|
Термопара | |||
| медь – константан | хромель – алюмель | хромель – копель | |
| 20 | |||
| … | |||
| 90 | |||
Оформление отчета
1. Привести схемы экспериментальных установок, данные измерительных приборов и исследуемых элементов, а также таблицы измерений.
2. По данным измерений табл. 1.1 построить график зависимости R ( q ). По графику R ( q ), а также по формулам (1.3), (1.5) рассчитать и занести в таблицу 1.1 значения a R, a r, и r для каждого из исследованных проводников. По данным таблицы 1.1 построить графики зависимостей R ( q ), r ( q ), a R ( q ) и a r ( q ).
3. Рассчитать длины свободного пробега электронов для исследованных проводников при комнатной температуре.
4. По данным таблицы 1.2 и по формуле (1.6) рассчитать средние значения относительной удельной термо-э.д.с. для исследованных термопар. построить графики зависимостей ЕТ( q ).
5. Привести краткое описание исследованных в работе материалов (химический состав, электрические свойства, области применения).
6. Дать краткие выводы по результатам работы.
Контрольные вопросы
1. Какие материалы относятся к классу проводников?
2. Чем обусловлена высокая электропроводность проводников?
3. Как можно классифицировать проводники?
4. Какие факторы и почему влияют на удельное электрическое сопротивление?
5. Что такое температурный коэффициент удельного сопротивления?
6. Для каких материалов и почему важно учитывать линейное расширение при нагревании?
7. Что такое термо-э.д.с., в чем причина ее возникновения?
8. Исходя из каких соображений подбираются материалы для термопар?
Работа 2. Исследование свойств терморезисторов
Цель работы:
а) определение зависимости сопротивления терморезисторов от температуры;
б) определение энергии активации и коэффициента температурной чувствительности полупроводника;
в) оценка величины постоянной времени тепловой инерции терморезисторов;
г) построение динамических вольтамперных характеристик терморезисторов.
Краткие сведения из теории
Терморезистором называется полупроводниковый резистор, сопротивление которого в сильной степени зависит от температуры.
Удельная электрическая проводимость полупроводников
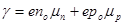, (2.1)
где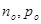 
– концентрация, 
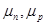– подвижность электронов и дырок соответственно.
В примесных (n-типа или p-типа) полупроводниках одним из слагаемых в приведенном выражении можно пренебречь.
Подвижность носителей при нагревании изменяется сравнительно слабо (по степенному закону, ~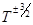 
), а концентрация очень сильно (по экспоненциальному закону, ~ 
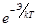). Поэтому температурная зависимость удельной проводимости полупроводников подобна температурной зависимости концентрации основных носителей, а электрическое сопротивление терморезисторов может быть определено по формуле:
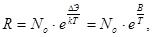(2.2)
где N о – коэффициент, зависящий от типа и геометрических размеров полупроводника; DЭ – энергия активации примесей (для примесных полупроводников) или ширина запрещенной зоны (для собственных полупроводников), k – постоянная Больцмана.
постоянная В = D Э/ k носит название коэффициент температурной чувствительности и приводится в паспортных данных на терморезистор. экспериментально коэффициент температурной чувствительности определяют по формуле
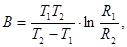(2.3)
где Т1 и Т 2 – исходная и конечная температуры рабочего температурного диапазона, R1 и R2 – сопротивления терморезистора при температуре соответственно Т 1 и Т 2.
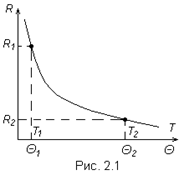На рис. 2.1 приведен график зависимости сопротивления полупроводникового резистора от температуры.
Чаще всего терморезисторы имеют отрицательный температурный коэффициент сопротивления a R. Выпускаются также терморезисторы, имеющие в сравнительно узком интервале температур положительный a R и называемые позисторами. При нагревании величина сопротивления терморезисторов убывает, а позисторов возрастает в сотни и тысячи раз. В справочниках значение a R приводится для температуры 20 оС. Значения a R терморезисторов для любой температуры в диапазоне 20…150 оС можно определить по формуле:
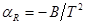(2.4)
терморезистор характеризуется определенной тепловой инерцией, зависящей от химических свойств полупроводника и конструкции элемента (площади излучающей поверхности). Тепловая инерция оценивается постоянной времени t – временем, за которое разность между собственной температурой тела и температурой среды уменьшается в е (2,7183) раз.
Если терморезистор, имеющий температуру q о, поместить в среду с температурой q с¹q о, то его температура будет изменяться с течением времени по показательному закону:
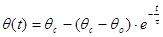. (2.5)
На рис.2.2 показан процесс изменения температуры терморезистора при его остывании.
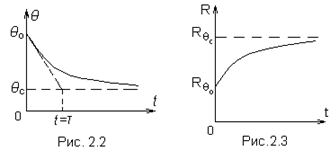
С остыванием терморезистора сопротивление его увеличивается (рис. 2.3). Знание зависимостей R ( q ) (рис.2.1) и R ( t ) (рис. 2.3) позволяет, задаваясь значениями R и определяя по кривым рис. 2.1 и 2.3 соответствующие им значения q и t, построить зависимость q ( t ) и определить t.
Различают статическую и динамическую вольтамперные характеристики (ВАХ) терморезистора. При снятии статической ВАХ ток фиксируется после длительной выдержки терморезистора при каждом значении напряжения. Динамическая ВАХ показывает реакцию терморезистора на воздействие импульсов напряжения разной величины, но одинаковой длительности. ток фиксируется в конце импульса.
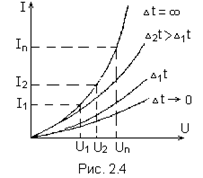
Терморезистор обладает одной статической и семейством динамических ВАХ, соответствующих ряду фиксированных длительностей D t импульсов напряжения. ВАХ терморезистора являются нелинейными. динамические ВАХ терморезистора приведены на рис. 2.4.
При длительности импульса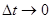 
терморезистор не успевает нагреться и сопротивление его практически не изменяется с ростом напряжения. При длительности 
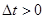терморезистор нагревается, и ВАХ становится существенно нелинейной. Чем больше длительность импульса, тем больше ток при одной и той же величине напряжения. Статическая ВАХ соответствует 
.
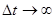Дата: 2019-07-24, просмотров: 205.
