Оглавление
Введение
Формирование понятия об инерции
Второй закон Ньютона
Методика формулирования понятия«масса тела»
Методика формулирования понятия «сила»
Измерение сил. Динамометр. Сложение сил
Зависимость между силой, массой и ускорением. Второй закон Ньютона
Закрепление и углубление материала на второй закон Ньютона
Третий закон Ньютона
Заключительное занятие по теме «законы движения Ньютона»
Список литературы
Вступление
Решение основной задачи механики - определение положения тел и любой момент времени — требует знания их начальных координат, скорости и ускорения, которые возникают при взаимодействии тел. Последнее является предметом изучения динамики.
Динамика составляет важнейшую часть классической механики. Ее главная задача – изучение взаимодействий тел, которыми объясняются, прежде всего, различные изменения их движений. В основе динамики лежат три закона. Впервые их в общем виде сформулировал гениальный английский физик Исаак Ньютон (1643 – 1727). Теперь эти законы называют его именем. Открытие законов движения Ньютона было подготовлено многовековой человеческой практикой, трудами многих поколений ученых. Законы механического движения с их многочисленными и важными следствиями имеют огромное научное и мировоззренческое значение. Они позволяют понять и объяснить многие явления и в космосе и в микромире. Классической механикой введены в науку важнейшие физические понятия: «масса», «сила», «импульс» (количество движения), энергия и др. особо отметим, что законы сохранения энергии и импульса не знают исключения в любых явлениях макро- и микромира. Законы классической механики составляют научную основу техники многих отраслей народного хозяйства: строительства, машиностроения, транспорта и др. поэтому изучения динамики следует в полной мере использовать в целях политехнического обучения учащихся. Показывая научную и практическую значимость законов механики, нужно вместе с тем в доступной форме дать учащимся первоначальные понятия и о границах применения. Учителю следует помнить, что было время, когда законы классической механики казались всеобъемлющими и способными объяснить и описать все явления природы. Наглядные образы, представления и понятия, почерпнутые учащимися в окружающей жизни, и теперь наталкивают их на «механическую» трактовку и «механические» образы при изучении вопросов физики, где они неприменимы. Многие явления природы не могут быть сведены только к механическому взаимодействию тел уже потому, что материя в природе существует не только в виде вещества, но и в виде поля. Явления, например, в электромагнитном поле подчиняются законам Максвелла, а не законам Ньютона. Но и движения, с которыми мы связываем определенные физические тела, не всегда могут быть объяснены законами Ньютона. Классическая механика не может удовлетворительно описать движения множествачастиц - молекул, объяснить законы, которым подчиняются элементарные частицы, движение тел со скоростями, близкими к скорости света. Соответствующие законы устанавливаются статистической механикой, квантовой механикой и теорией относительности. Определенные сведения о данных разделах современной физики учащиеся получают в старших классах. Однако некоторые первоначальные представления о границах применимости законов Классической механики ученики должны получить уже в самом начале изучении физики.
При этом учащиеся должны осознать, что успехи современной науки вовсе не отрицают и не зачеркивают механику Ньютона. Более того (согласно принципу соответствия), они утверждают незыблемость ее законов для определенных предельных условий: классическая механика - это механика макротел, движущихся со скоростями, далекими от скорости света. Данные условия выполняются в огромной сфере практической и научной деятельности человека на Земле и в космосе. В этом и заключается непреходящее значение механики Ньютона.
При изучении динамики в VIII классе следует принять во внимание знания учащихся по механике, полученные в VI классе, а также их жизненный опыт и представления.
Основное содержание учебного материала видно наследующего возможного варианта примерного поурочного планирования темы:
1-й урок. Понятие с динамике. Закон инерции. Краткие сведения о жизни и научном подвиге Галилео Галилея.
2-й урок. Взаимодействие тел. Ускорение тел при взаимодействии.
3-й урок. Масса тел как мера их инерциальных свойств.
4-й урок. Масса тел как мера их гравитационных свойств.
5-й урок. Определение массы тел взвешиванием. Сила.
6-й урок. Второй закон Ньютона. Единица силы в СИ.
7-й урок. Измерение сил. Динамометр. Сложение сил.
8-й и 9-й урок. Углубление и закрепление материала на второй закон Ньютона. Решение задач.
10-й урок. Третий закон Ньютона. Решение задач.
11-й урок. Повторений и обобщение пройденного (краткие сведения о жизни и научной деятельности И. Ньютона).
Из истории открытия закона инерции. При изучении данного материала несомненную пользу принесут сведения из истории открытия закона инерции. В адаптированном виде они могут быть использованы и на первом, и на последующих уроках, а также на внеклассных занятиях.
Повседневные наблюдения и практический опыт приводили человека к мысли о том, что тела не приходят в движение сами собой. Для перемещения тел их надо тянуть, толкать, словом прилагать к ним некоторую «силу». Аристотель (384—322) называл такие движения насильственными и считал, что они прекращаются по прекращению действия силы. Отсюда следовал вывод: движение тел обусловлено действием на них сил. Ошибка таких рассуждений, как известно, заключается в том, что в них не принимаются во внимание силы, препятствующие движению.
Наряду с указанными взглядами постепенно возникла мысль о том, что существует и некая «внутренняя» сила, ответственная за движение тел. «Всякое движение,— писал Леонардо да Винчи (1452—1519),— стремится к своему сохранению, или каждое тело движется постоянно, пока в нем сохраняется действие его двигателя». Другой итальянский ученый Джованни Батиста Бенедетти (1530—1590) ввел «представление об «импето» («впечатление»), сохраняющемся в теле, которому сообщается скорость. Следующий шаг делает Галилео Галилей (1564 — 1642). Он детально изучил движение тел по наклонной плоскости. Галилей экспериментально доказал, что шар скатывается по наклонной плоскости ускоренно, а поднимается замедленно. На этом основании он сделал вывод: «Когда тело движется по горизонтальной плоскости, не встречая никакого сопротивления движению, то … движение его является равномерным и продолжалось бы бесконечно, если бы плоскость простиралась в пространстве без конца. Галилей еще не даст общей формулировки принципа инерции. Он связывает открытое им свойство тел только с их движением в горизонтальном направлении (и ошибочно с движением по идеально гладкой поверхности земного шара). Но он первый понимает явление инерции столь глубоко и правильно применяет его. В его формулировке впервые производится абстрагирование от сопротивления движению тел. Однако Галилей еще не располагает обобщенным понятием силы и не принимает в явном виде во внимание силы реакции опоры и силу тяжести.
Впервые от действия тяготения абстрагируется Рене Декарт (1596—1650). «Полагаю, — писал он, — что природа движения такова, что, если тело пришло в движение, уже этого достаточно, чтобы оно его продолжало с той же скоростью и в направлении топ же прямой линии, пока оно не будет остановлено или отклонено какой-либо другой причиной».
На новую ступень обобщения, опираясь на труды своих предшественников, и прежде всего Галилея, закон инерции поднял И. Ньютон, который включил его в число важнейших трех аксиом или законов движения в следующем виде: всякое тело продолжает удерживаться в своем состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Поскольку всякое движение относительно, возникает вопрос: что принять за систему отсчета? Движение одного и того же тела в одной системе отсчета может быть равномерным и прямолинейным, а в другой в то же самое время — переменным и криволинейным.
Галилей считал закон инерции справедливым в системе отсчета, связанной с Землей, а Ньютон ввел понятие абсолютного пространства, которое «по самой своей сущности и безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным».
Определение Ньютона лишено физического смысла, поскольку нельзя построить систему отсчета, не связав ее с конкретными телами. В системе же отсчета, связанной с Землей, закон инерции, строго говоря, не выполняется, как во всякой вращающейся системе (этот факт, как уже указывалось, привел Галилея к ошибочному утверждению о справедливости закона инерции для равномерного движения тел по окружности). Тем не менее, фундаментальный закон механики — закон инерции был открыт. Объясняется это тем, что для системы «Земля», в которой практически и велись все многовековые наблюдения, отступления от закона инерции относительно невелики. Эта система с достаточной для практических целей точностью может быть принята за инерциальную. Практически точно закон инерции выполняется в системе отсчета, связанной с «неподвижными» звездами.
Второй закон Ньютона
Опыт и логика подсказывают, что если действующие на тело силы не уравновешиваются, то его движение должно изменяться. Существующую при этом количественную закономерность удалось впервые сформулировать в своих «Началах» И. Ньютону в виде следующей аксиомы или закона движения: Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Математическизаконвыражается формулой 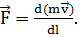 Все величины, входящие в эту формулу: сила
Все величины, входящие в эту формулу: сила 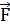 , масса m, количество движения
, масса m, количество движения 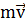 и время t, у Ньютона независимые.
и время t, у Ньютона независимые.
В настоящее время в учебниках физики второй закон Ньютона чаще всего записывается в виде. 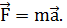 (Впервые выражение силы, как величины, равной массе, умноженной на ускорение, дается в «Механике» Эйлера; 1736 г.) Следует, однако, иметь в виду, что зависимость.
(Впервые выражение силы, как величины, равной массе, умноженной на ускорение, дается в «Механике» Эйлера; 1736 г.) Следует, однако, иметь в виду, что зависимость. 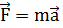 не эквивалентна полностью формуле
не эквивалентна полностью формуле 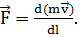 Она верна только при условии m =const, что практически имеет место при скоростях, далеких от скорости света, когда зависимостью массы от скорости можно пренебречь.
Она верна только при условии m =const, что практически имеет место при скоростях, далеких от скорости света, когда зависимостью массы от скорости можно пренебречь.
Из сказанного выше следует, что для изучения второго закона Ньютона в форме 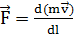 предварительно требуется ввести понятия массы, силы и ускорения. Различные методические системы изучения второго закона Ньютона отличаются в основном тем, как вводятся данные фундаментальные физические понятия.
предварительно требуется ввести понятия массы, силы и ускорения. Различные методические системы изучения второго закона Ньютона отличаются в основном тем, как вводятся данные фундаментальные физические понятия.
Наиболее распространенной системой является такое построение учебного материала, когда массу и силу стараются определить независимо друг от друга и от второго закона Ньютона: массу путем взвешивания на весах, а силу — статическим методом — с помощью пружинных динамометров, которые градуируют весом гирь. При этом масса иногда трактуется как мера количества вещества в теле. Такой упрощенный, устаревший подход к формированию важнейших понятий динамики для советской школы неприемлем.
В настоящее время многие методисты считают предпочтительной такую систему, при которой сначала вводится понятие силы. При этом сила трактуется как «мера действия тел друг на друга, в результате которого тела получают ускорения». После этого изучаются способы измерения сил с помощью эталонных пружин или динамометров, и устанавливается зависимость ускорения тел от сил: 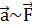
«Величину 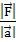 , равную отношению модуля силы к модулю ускорения, называют массой (точнее, инертной массой)».
, равную отношению модуля силы к модулю ускорения, называют массой (точнее, инертной массой)».
Масса тела выступает как коэффициент пропорциональности между силой и ускорением 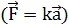 ,а соотношение
,а соотношение 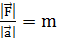 выступает как определение массы и второй закон Ньютона. При данном методическом подходе в качестве основной единицы выступает единица силы, что противоречит системе СИ.
выступает как определение массы и второй закон Ньютона. При данном методическом подходе в качестве основной единицы выступает единица силы, что противоречит системе СИ.
Понятие о силе вводится на основе уравнения 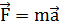 , которое одновременно является и определением силы и вторым законом Ньютона. По мнению многих методистов в этом заключается главная трудность этого подхода. Выход из данного положения находится за счет использования других физических законов, определяющих зависимость силы от других величин, например, от координат.
, которое одновременно является и определением силы и вторым законом Ньютона. По мнению многих методистов в этом заключается главная трудность этого подхода. Выход из данного положения находится за счет использования других физических законов, определяющих зависимость силы от других величин, например, от координат.
Третий закон Ньютона
Изучение третьего закона Ньютона начинают с повторения опытов по взаимодействию тел (см. рис. 5), обращая внимание при этом на то, что каждое из тел действует на другое с некоторой силой.
После этого следует еще раз рассмотреть взаимодействие двух тел при их вращательном движении (см, рис. 9) и записать известное учащимся соотношение 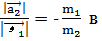 виде
виде 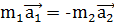 .
.
Так как и 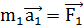 и
и 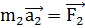 , где
, где 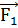 и
и 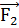 - это силы, приложенные соответственно к первому и второму телам, то
- это силы, приложенные соответственно к первому и второму телам, то 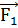 =-
=- 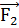 . Это равенство выражает третий закон Ньютона. Словесная его формулировка в учебной литературе различна.
. Это равенство выражает третий закон Ньютона. Словесная его формулировка в учебной литературе различна.
В некоторых учебниках этот закон приводится в той формулировке, которая была дана в «Началах» самим Ньютоном: «Действию всегда есть равное и противоположное противодействие, другими словами, действия двух тел друг на друга всегда равны и направлены в противоположные стороны».
Еще чаще этот закон формулируется как утверждение, что «сила действия равна силе противодействия» или еще более кратко: «действие равно противодействию».
Как показывает педагогическая практика, в этих кратких формулировках третий закон Ньютона хорошо запоминается учащимися, но далеко не всегда глубоко понимается. Поэтому лучше дать более обстоятельную и исчерпывающую формулировку: силы, с которыми действуют друг на друга тела, по абсолютному значению равны и направлены по одной и той же прямой в противоположные стороны.
Силы, о которых идет речь в третьем законе Ньютона, всегда одной природы. Приложены они к различным телам и потому не имеют равнодействующей. На опытах следует показать, что силы всегда возникают парами. Если есть одна сила, то есть и другая, равная ей по модулю, но противоположная по направлению.

Рис. 16
К динамометру (рис. 16) подвешивают тело 2, например цилиндр от ведерка Архимеда, а на столик динамометра 3 ставят сосуд 4 с водой (стрелки обоих динамометров лучше установить на нуле). Опуская цилиндр 2 в сосуд 4, наблюдают одновременное, равное и противоположное изменение показаний обоих динамометров.
На внеклассных занятиях, особенно на вечерах занимательной физики, возможно решение большого числа интересных и поучительных занимательных задач, софизмов и парадоксов. В качестве примера приведем одну из таких задач:
На рычажных весах уравновешен стакан с водой. Нарушится ли равновесие весов, если в воду погрузить карандаш и держать его в руках, не касаясь стенок стакана? Проверить ответ на опыте. (Вода не должна выливаться из стакана.)
Неожиданный для учащихся результат опыта объясняется тем, что не только вода действует с архимедовой силой на карандаш, но и карандаш с равной по модулю, но противоположной по направлению силой действует на воду.
Список литературы
1.Бугаев А.И. Методика преподавания физики в средней школе М.,1981
2.Перышкин А.В. и др. Методика преподавания физики в 6-7 кл. средней школы. М .,1985.
3.Методика преподавания физики в средней школе. Частные вопросы. под ред. С.Е.Каменецкого и др. М .,1987
4.Методика преподавания физики в средней школе. 4.1 и 4.2. /под ред. Усовой А.В. и др. М., 1990.
5.Внеурочная работа по физике/ Под ред. О.Ф.Кабардина. -М.: Просвещение, 1983.
6.Резников Л.И. Преподавание физики в средних профессионально-технических училищах.-М.:Высшая школа, 1977.
7.Демонстрационный эксперимент по физике в средней школе; В 2-х частях./Под ред. А.А.Покровского.-М.:Просвящение, 1978.
8.Марголис А.А.,Парфеньтьева Н.Е., Иванова А.А. Практикум по школьному физическому эксперименту.-М.:Просвящение, 1977.
Оглавление
Введение
Формирование понятия об инерции
Второй закон Ньютона
Методика формулирования понятия«масса тела»
Методика формулирования понятия «сила»
Измерение сил. Динамометр. Сложение сил
Зависимость между силой, массой и ускорением. Второй закон Ньютона
Закрепление и углубление материала на второй закон Ньютона
Третий закон Ньютона
Заключительное занятие по теме «законы движения Ньютона»
Список литературы
Вступление
Решение основной задачи механики - определение положения тел и любой момент времени — требует знания их начальных координат, скорости и ускорения, которые возникают при взаимодействии тел. Последнее является предметом изучения динамики.
Динамика составляет важнейшую часть классической механики. Ее главная задача – изучение взаимодействий тел, которыми объясняются, прежде всего, различные изменения их движений. В основе динамики лежат три закона. Впервые их в общем виде сформулировал гениальный английский физик Исаак Ньютон (1643 – 1727). Теперь эти законы называют его именем. Открытие законов движения Ньютона было подготовлено многовековой человеческой практикой, трудами многих поколений ученых. Законы механического движения с их многочисленными и важными следствиями имеют огромное научное и мировоззренческое значение. Они позволяют понять и объяснить многие явления и в космосе и в микромире. Классической механикой введены в науку важнейшие физические понятия: «масса», «сила», «импульс» (количество движения), энергия и др. особо отметим, что законы сохранения энергии и импульса не знают исключения в любых явлениях макро- и микромира. Законы классической механики составляют научную основу техники многих отраслей народного хозяйства: строительства, машиностроения, транспорта и др. поэтому изучения динамики следует в полной мере использовать в целях политехнического обучения учащихся. Показывая научную и практическую значимость законов механики, нужно вместе с тем в доступной форме дать учащимся первоначальные понятия и о границах применения. Учителю следует помнить, что было время, когда законы классической механики казались всеобъемлющими и способными объяснить и описать все явления природы. Наглядные образы, представления и понятия, почерпнутые учащимися в окружающей жизни, и теперь наталкивают их на «механическую» трактовку и «механические» образы при изучении вопросов физики, где они неприменимы. Многие явления природы не могут быть сведены только к механическому взаимодействию тел уже потому, что материя в природе существует не только в виде вещества, но и в виде поля. Явления, например, в электромагнитном поле подчиняются законам Максвелла, а не законам Ньютона. Но и движения, с которыми мы связываем определенные физические тела, не всегда могут быть объяснены законами Ньютона. Классическая механика не может удовлетворительно описать движения множествачастиц - молекул, объяснить законы, которым подчиняются элементарные частицы, движение тел со скоростями, близкими к скорости света. Соответствующие законы устанавливаются статистической механикой, квантовой механикой и теорией относительности. Определенные сведения о данных разделах современной физики учащиеся получают в старших классах. Однако некоторые первоначальные представления о границах применимости законов Классической механики ученики должны получить уже в самом начале изучении физики.
При этом учащиеся должны осознать, что успехи современной науки вовсе не отрицают и не зачеркивают механику Ньютона. Более того (согласно принципу соответствия), они утверждают незыблемость ее законов для определенных предельных условий: классическая механика - это механика макротел, движущихся со скоростями, далекими от скорости света. Данные условия выполняются в огромной сфере практической и научной деятельности человека на Земле и в космосе. В этом и заключается непреходящее значение механики Ньютона.
При изучении динамики в VIII классе следует принять во внимание знания учащихся по механике, полученные в VI классе, а также их жизненный опыт и представления.
Основное содержание учебного материала видно наследующего возможного варианта примерного поурочного планирования темы:
1-й урок. Понятие с динамике. Закон инерции. Краткие сведения о жизни и научном подвиге Галилео Галилея.
2-й урок. Взаимодействие тел. Ускорение тел при взаимодействии.
3-й урок. Масса тел как мера их инерциальных свойств.
4-й урок. Масса тел как мера их гравитационных свойств.
5-й урок. Определение массы тел взвешиванием. Сила.
6-й урок. Второй закон Ньютона. Единица силы в СИ.
7-й урок. Измерение сил. Динамометр. Сложение сил.
8-й и 9-й урок. Углубление и закрепление материала на второй закон Ньютона. Решение задач.
10-й урок. Третий закон Ньютона. Решение задач.
11-й урок. Повторений и обобщение пройденного (краткие сведения о жизни и научной деятельности И. Ньютона).
Из истории открытия закона инерции. При изучении данного материала несомненную пользу принесут сведения из истории открытия закона инерции. В адаптированном виде они могут быть использованы и на первом, и на последующих уроках, а также на внеклассных занятиях.
Повседневные наблюдения и практический опыт приводили человека к мысли о том, что тела не приходят в движение сами собой. Для перемещения тел их надо тянуть, толкать, словом прилагать к ним некоторую «силу». Аристотель (384—322) называл такие движения насильственными и считал, что они прекращаются по прекращению действия силы. Отсюда следовал вывод: движение тел обусловлено действием на них сил. Ошибка таких рассуждений, как известно, заключается в том, что в них не принимаются во внимание силы, препятствующие движению.
Наряду с указанными взглядами постепенно возникла мысль о том, что существует и некая «внутренняя» сила, ответственная за движение тел. «Всякое движение,— писал Леонардо да Винчи (1452—1519),— стремится к своему сохранению, или каждое тело движется постоянно, пока в нем сохраняется действие его двигателя». Другой итальянский ученый Джованни Батиста Бенедетти (1530—1590) ввел «представление об «импето» («впечатление»), сохраняющемся в теле, которому сообщается скорость. Следующий шаг делает Галилео Галилей (1564 — 1642). Он детально изучил движение тел по наклонной плоскости. Галилей экспериментально доказал, что шар скатывается по наклонной плоскости ускоренно, а поднимается замедленно. На этом основании он сделал вывод: «Когда тело движется по горизонтальной плоскости, не встречая никакого сопротивления движению, то … движение его является равномерным и продолжалось бы бесконечно, если бы плоскость простиралась в пространстве без конца. Галилей еще не даст общей формулировки принципа инерции. Он связывает открытое им свойство тел только с их движением в горизонтальном направлении (и ошибочно с движением по идеально гладкой поверхности земного шара). Но он первый понимает явление инерции столь глубоко и правильно применяет его. В его формулировке впервые производится абстрагирование от сопротивления движению тел. Однако Галилей еще не располагает обобщенным понятием силы и не принимает в явном виде во внимание силы реакции опоры и силу тяжести.
Впервые от действия тяготения абстрагируется Рене Декарт (1596—1650). «Полагаю, — писал он, — что природа движения такова, что, если тело пришло в движение, уже этого достаточно, чтобы оно его продолжало с той же скоростью и в направлении топ же прямой линии, пока оно не будет остановлено или отклонено какой-либо другой причиной».
На новую ступень обобщения, опираясь на труды своих предшественников, и прежде всего Галилея, закон инерции поднял И. Ньютон, который включил его в число важнейших трех аксиом или законов движения в следующем виде: всякое тело продолжает удерживаться в своем состоянии покоя или равномерного прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Поскольку всякое движение относительно, возникает вопрос: что принять за систему отсчета? Движение одного и того же тела в одной системе отсчета может быть равномерным и прямолинейным, а в другой в то же самое время — переменным и криволинейным.
Галилей считал закон инерции справедливым в системе отсчета, связанной с Землей, а Ньютон ввел понятие абсолютного пространства, которое «по самой своей сущности и безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным».
Определение Ньютона лишено физического смысла, поскольку нельзя построить систему отсчета, не связав ее с конкретными телами. В системе же отсчета, связанной с Землей, закон инерции, строго говоря, не выполняется, как во всякой вращающейся системе (этот факт, как уже указывалось, привел Галилея к ошибочному утверждению о справедливости закона инерции для равномерного движения тел по окружности). Тем не менее, фундаментальный закон механики — закон инерции был открыт. Объясняется это тем, что для системы «Земля», в которой практически и велись все многовековые наблюдения, отступления от закона инерции относительно невелики. Эта система с достаточной для практических целей точностью может быть принята за инерциальную. Практически точно закон инерции выполняется в системе отсчета, связанной с «неподвижными» звездами.
Формирование понятия об инерции
Различные методические подходы к изучению закона инерции отличаются в основном тем, к какой конечной формулировке — классической ньютоновской или же к формулировке, принимающей во внимание уравновешенные силы,— подводят учащихся.
Рассмотрим каждый из этих основных подходов и некоторые их модификации подробнее. При этом будем иметь в виду, что все законы движения Ньютона относятся, строго говоря, к материальным точкам и к телам, совершающим поступательное движение.
Согласно первому, наиболее распространенному подходу выясняется вопрос, почему останавливаются движущиеся тела и что нужно сделать для того, чтобы их движение продолжалось как можно дольше.
С помощью мысленных или реально поставленных на демонстрационном столе экспериментов устанавливают, что движение тел, например шара по горизонтальной поверхности стола, будет изменяться тем меньше, чем меньше сопротивление его движению, в данном случае сила трения.
Отсюда для предельного случая, когда силами трения можно пренебречь, делается вывод, что если на тело не действуют другие тела, то тело сохраняет состояние покоя или равномерного прямолинейного движения относительно Земли. Далее в некоторых пособиях уточняется, что закон инерции выполняется практически точно в гелиоцентрической системе. Таким образом, закон инерции по существу формулируется так же, как и у Ньютона для предельного случая, когда тела достаточно удалены от всех других тел. Вначале на конкретных примерах вводится понятие о «компенсации действия тел» и применительно к некоторым конкретным системам отсчета, прежде всего к Земле, показывается справедливость закона инерции.
На основе конкретных примеров первый закон Ньютона формулируется в следующем виде: существуют такие системы отсчета, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной; если на них не действуют другие тела, или действие других тел компенсируется. Такие системы отсчета называются инерциальными.
Данная формулировка закона инерции по сравнению с приведенными выше является наиболее полной. Она охватывает и предельные, и реально имеющие место в окружающей жизни случаи. Кроме того, в ней указывается на справедливость закона только в определенных, инерциальных системах отсчета.
Однако данный методический подход также не лишен недостатков и трудностей:
1)вводится дополнительное, притом недостаточно с физической точки зрения определенное понятие о «компенсации действия тел»;
2) в данной формулировке на первом плане оказывается мысль о существовании инерциальных систем, а не о явлении инерции;
3)не говорится в явном виде о прямолинейности движения тел по инерции;
4)данная формулировка из-за того, что несет большую информацию,сложнее предыдущей. Для устранения указанных выше трудностей необходимо максимально использовать знания учащихся из курса физики, пройденного ранее и формировать весь комплекс понятий о законе инерции по частям.
Крайне желательно, чтобы учащиеся предварительно самостоятельно повторили соответствующий материал по учебнику и восстановили в своей памяти определение: явление сохранения скорости тела при отсутствии действия на него других тел называют инерцией. Соответствующие примеры всегда приведут сами учащиеся. Здесь уместно также рассказать об опытах Галилея с наклонной плоскостью, интересных не только своими выводами, но и примером сочетания логического абстрактного мышления с реальным физическим экспериментом. Затем можно также сказать о взгляде древних и неправильном бытовом представлении людей, незнакомых с физикой, о том, что движение есть результат взаимодействия тел. После этого повторения и исторического введения можно перейти к более детальному и обстоятельному рассмотрению инерции с учетом реально существующих взаимодействий тел.
Вначале следует рассмотреть приведенный в учебнике пример с находящимся в состоянии покоя шаром, подвешенным на пружине или резиновом шнуре. При этом, как показывает опыт преподавания, можно не только говорить в общих выражениях о том, что «действия на шар двух тел — шнура и Земли компенсируют (иногда говорят уравновешивают) друг друга», но и указать на чертеже в явном виде действующие на тело силы: силу тяжести Fт и силу упругости (рис. 1).

рис. 1
Понятие «сила» в данном случае не расширяется и не углубляется. Оно используется как синоним выражения «действие одного тела на другое», которое, как известно из курса физики VI класса, может быть измерено динамометром и выражено в ньютонах.
В качестве упражнения и закрепления полученных понятий можно дать учащимся задание самостоятельно указать и изобразить графически силы, действующие на гирю, помещенную на пружину (рис. 2 а) и на шайбу, которая лежит на льду (рис. 2 б).
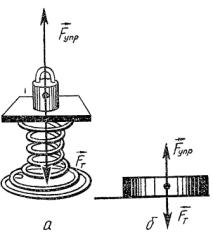
рис.2
На основе данных и аналогичных примеров делают вывод, что если на тело действуют равные по модулю, но противоположно направленные силы, то тело может находиться в состоянии покоя. Иначе можно сказать, что действие тел в этом случае компенсируется.
Затем переходят к рассмотрению наиболее важного и сложного случая — движения тела по инерции, используя описанный в учебнике пример с шайбой. Полезно еще раз изобразить шайбу и действующие на нее силы, включая небольшую силу трения Fтр (рис. 3 а), а также вектор скорости V. Как опытный факт констатируем, что после удара шайба движется прямолинейно и ее скорость изменяется незначительно. Естественно предположить, как это делалось уже раньше при рассмотрении опыта Галилея, что скорость тела не изменилась бы совсем, если бы сил трения не было вовсе.
Этот вывод желательно подкрепить выразительными опытами с движением по инерции с крайне малым трением дисков из сухого льда или же тел на воздушной подушке.
Далее высказывается мысль, что силу трения можно компенсировать. Последнее легко осуществить, равномерно перемещая шайбу, например, с помощью клюшки, непрерывно подталкивающей ее с силой 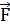 , равной и противоположно направленной силе трения (рис. 3 б).
, равной и противоположно направленной силе трения (рис. 3 б).

рис. 3
Простейшим наглядным примером равномерного движения, легко осуществимого на опыте, является движение шарика или бруска по наклонной плоскости, которой придан такой уклон, чтобы сила трения компенсировалась равнодействующей силы реакции желоба и силы тяжести.
Обобщая пройденное, делают вывод, с которым учащиеся уже знакомились: материал о сложении сил, направленных по одной прямой: «Тело под действием двух равных и противоположно направленных сил будет находиться в покое или двигаться равномерно и прямолинейно».
Наконец, должно быть сформировано первоначальное понятие об инерциальных системах отсчета. До сих пор во всех опытах и примерах за систему отсчета, в которой оказывался справедливым закон инерции, принималась Земля. На конкретных примерах следует показать, что закон инерции выполняется также в системах отсчета, движущихся равномерно и прямолинейно относительно Земли.
Все опыты по инерции, рассмотренные выше, с равным успехом и теми же результатами можно провести, например, в равномерно движущихся поезде, теплоходе или самолете.
В результате проделанной работы учащиеся должны усвоить, что тело сохраняет состояние покоя или равномерного прямолинейного поступательного движения в инерциальных системах отсчета, если на него не действуют другие тела или если силы, с которыми они действуют, уравновешиваются.
Для закрепления и углубления полученных понятий в классе и дома учащиеся решают в основном качественные задачи-вопросы. Желательно, однако, и решение несложных экспериментальных задач, например, такой:
Объяснить, какие уравновешенные силы действуют на движущийся равномерно вниз шарик в стеклянной трубке с водой (рис. 4 а); на поднимающийся равномерно вверх пузырек воздуха (рис. 4 б).
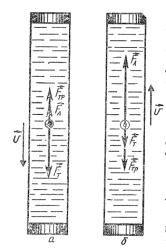
Рис. 4
Необходимо также решение задач политехнического содержания:
Плуг равномерно движется по борозде. Можно ли сказать, что он движется по инерции?
Интересна задача «Самый легкий способ путешествовать», составленная по материалам «Занимательной физики» Я.И. Перельмана.
Второй закон Ньютона
Опыт и логика подсказывают, что если действующие на тело силы не уравновешиваются, то его движение должно изменяться. Существующую при этом количественную закономерность удалось впервые сформулировать в своих «Началах» И. Ньютону в виде следующей аксиомы или закона движения: Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Математическизаконвыражается формулой 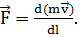 Все величины, входящие в эту формулу: сила
Все величины, входящие в эту формулу: сила 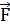 , масса m, количество движения
, масса m, количество движения 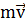 и время t, у Ньютона независимые.
и время t, у Ньютона независимые.
В настоящее время в учебниках физики второй закон Ньютона чаще всего записывается в виде. 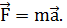 (Впервые выражение силы, как величины, равной массе, умноженной на ускорение, дается в «Механике» Эйлера; 1736 г.) Следует, однако, иметь в виду, что зависимость.
(Впервые выражение силы, как величины, равной массе, умноженной на ускорение, дается в «Механике» Эйлера; 1736 г.) Следует, однако, иметь в виду, что зависимость. 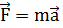 не эквивалентна полностью формуле
не эквивалентна полностью формуле 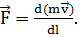 Она верна только при условии m =const, что практически имеет место при скоростях, далеких от скорости света, когда зависимостью массы от скорости можно пренебречь.
Она верна только при условии m =const, что практически имеет место при скоростях, далеких от скорости света, когда зависимостью массы от скорости можно пренебречь.
Из сказанного выше следует, что для изучения второго закона Ньютона в форме 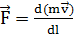 предварительно требуется ввести понятия массы, силы и ускорения. Различные методические системы изучения второго закона Ньютона отличаются в основном тем, как вводятся данные фундаментальные физические понятия.
предварительно требуется ввести понятия массы, силы и ускорения. Различные методические системы изучения второго закона Ньютона отличаются в основном тем, как вводятся данные фундаментальные физические понятия.
Наиболее распространенной системой является такое построение учебного материала, когда массу и силу стараются определить независимо друг от друга и от второго закона Ньютона: массу путем взвешивания на весах, а силу — статическим методом — с помощью пружинных динамометров, которые градуируют весом гирь. При этом масса иногда трактуется как мера количества вещества в теле. Такой упрощенный, устаревший подход к формированию важнейших понятий динамики для советской школы неприемлем.
В настоящее время многие методисты считают предпочтительной такую систему, при которой сначала вводится понятие силы. При этом сила трактуется как «мера действия тел друг на друга, в результате которого тела получают ускорения». После этого изучаются способы измерения сил с помощью эталонных пружин или динамометров, и устанавливается зависимость ускорения тел от сил: 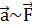
«Величину 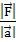 , равную отношению модуля силы к модулю ускорения, называют массой (точнее, инертной массой)».
, равную отношению модуля силы к модулю ускорения, называют массой (точнее, инертной массой)».
Масса тела выступает как коэффициент пропорциональности между силой и ускорением 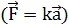 ,а соотношение
,а соотношение 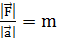 выступает как определение массы и второй закон Ньютона. При данном методическом подходе в качестве основной единицы выступает единица силы, что противоречит системе СИ.
выступает как определение массы и второй закон Ньютона. При данном методическом подходе в качестве основной единицы выступает единица силы, что противоречит системе СИ.
Понятие о силе вводится на основе уравнения 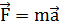 , которое одновременно является и определением силы и вторым законом Ньютона. По мнению многих методистов в этом заключается главная трудность этого подхода. Выход из данного положения находится за счет использования других физических законов, определяющих зависимость силы от других величин, например, от координат.
, которое одновременно является и определением силы и вторым законом Ньютона. По мнению многих методистов в этом заключается главная трудность этого подхода. Выход из данного положения находится за счет использования других физических законов, определяющих зависимость силы от других величин, например, от координат.
Дата: 2019-07-24, просмотров: 362.