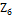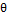Задача линейного программирования
Курсовая работа
Студента группы 315-ПО
Андреева Дмитрия Александровича
Руководитель курсовой работы
Васильева Наталья Анатольевна
Псков 2009 г.
Содержание
Введение
Глава Ι Линейное программирование
§ 1 Общая постановка задачи линейного программирования
§ 2 Математическая модель задачи линейного программирования
§ 3 Каноническая форма задачи линейного программирования
Глава ΙΙ Решение задачи симплексным методом
§ 1 Постановка задачи
§ 2 Составление математической модели задачи
§ 3 Алгоритмы решения задачи симплексным методом
§ 4 Построение начального опорного решения методом Гаусса
§ 5 Решение задачи
§ 6 Вывод
Заключение
Литература
Введение
В настоящее время множество задач планирования и управления в отраслях народного хозяйства, а также большой объём частных прикладных задач решаются методами математического программирования. Наиболее развитыми в области решения оптимизационных задач являются методы линейного программирования. Эти методы позволяют описать с достаточной точностью широкого круга задач коммерческой деятельности, таких, как планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров; распределение работников торговли должностям; организация рациональных закупок продуктов питания; распределение ресурсов; планирование капиталовложений; оптимизация межотраслевых связей; замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади; установление рационального режима работы.
В задачах линейного программирования критерий эффективности и функции в системе ограничений линейны.
Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования.
Если в задаче математического программирования имеется переменная времени, а критерий эффективности выражается через уравнения, описывающие течение операций во времени, то такая задача является задачей динамического программирования.
Во многих экономических моделях зависимости между постоянными и переменными факторами можно считать линейными.
Использование методов математического программирования в коммерческой деятельности связано со сбором необходимой информации коммерсантом, экономистом, финансистом, затем постановкой задачи вместе с математикой. Поскольку методы математического программирования уже реализованы на компьютере в виде пакета стандартных программ, то доступ к ним обычно прост, автоматизирован и не составляет особых трудностей.
Тогда эксплуатация модели включает в себя сбор и обработку информации, ввод обработанной информации в ЭВМ, расчеты на основе разработанных программ календарных планов и, наконец, выдачу результатов вычислений (в удобном для пользователей виде) для их использования в сфере производственной деятельности.
Глава Ι Линейное программирование
Постановка задачи
На предприятии в процессе производства используется 3 вида станков Ι, ІΙ, ІΙІ. При этом расходуется сырьё, трудовые ресурсы, и учитываются накладные расходы.
Известно, что для изготовления станка Ι – ого вида требуется 4 ед. сырья, 2 ед. трудовых ресурсов и 10 ед. накладных расходов; станка ΙІ – ого вида 6 ед. сырья, 2 ед. трудовых ресурсов и 8 ед. накладных расходов; для станка ΙΙІ – ого вида требуется 4 ед. сырья, 2 ед. трудовых ресурсов и 18 ед. накладных расходов; Предприятие имеет в наличии 420 ед. сырья, 120 ед. трудовых ресурсов и 250 ед. накладных ресурсов.
Прибыль от реализации станка І вида - 28 тыс. руб., ІΙ вида - 24 тыс. руб., ΙІΙ вида - 20 тыс. руб. Условия производства требует, чтобы трудовые ресурсы были использованы полностью, а накладные расходы были бы не менее имеющихся в наличии.
Составить план производства станков, обеспечивающих максимальную прибыль.
Решение задачи
Составляем симплексную таблицу
Симплексная таблица 1
| Б |
| -452 | -123,2 | 0 | 0 | 0 | -38 |
|
| 
| 
| 
| 
| 
| |||
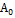
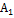
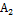
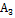
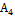
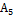
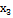
| 0 | 13 | -2,2 | 1 | 0 | 0 | -0,5 | |
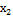
| 0 | 8 | 11,8 | 1 | 0 | 0 | 2 | |
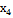
| 0 | 274 | 2,4 | 0 | 0 | 1 | 1 | |
|
| 452 | 123,2 | 0 | 0 | 0 | 38 | ||
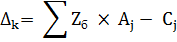
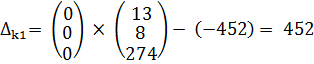
т. к все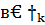 
> 0 решение оптимальное
Ответ: max Z(X) = 452 при X = (0; 8; 13)
Вывод
Максимальная прибыль в размере 425 тыс. руб. может быть достигнута, если производить 8 станков ІΙ вида, 13 станков ІΙІ вида и не производить станки Ι вида.
При этом расходуется 146 ед. сырья, 120 ед. трудовых ресурсов и 250 ед. накладных расходов.
Заключение
Данная курсовая работа посвящена вопросу о решении задачи линейного программирования методом последовательного улучшения плана, иначе симплекс – метод. Состоит из введения, двух глав, заключения и списка литературы.
В первой главе рассказывается о линейном программировании в частности, и о том, что такое общая постановка задачи линейного программирования, как составить математическую модель, а также рассказано о канонической форме задач линейного программирования.
Вторая глава работы посвящена практической части решения задачи. Строится математическая модель, решается задача симплексным методом, а также методом Гаусса.
Задача линейного программирования
Курсовая работа
Студента группы 315-ПО
Андреева Дмитрия Александровича
Руководитель курсовой работы
Васильева Наталья Анатольевна
Псков 2009 г.
Содержание
Введение
Глава Ι Линейное программирование
§ 1 Общая постановка задачи линейного программирования
§ 2 Математическая модель задачи линейного программирования
§ 3 Каноническая форма задачи линейного программирования
Глава ΙΙ Решение задачи симплексным методом
§ 1 Постановка задачи
§ 2 Составление математической модели задачи
§ 3 Алгоритмы решения задачи симплексным методом
§ 4 Построение начального опорного решения методом Гаусса
§ 5 Решение задачи
§ 6 Вывод
Заключение
Литература
Введение
В настоящее время множество задач планирования и управления в отраслях народного хозяйства, а также большой объём частных прикладных задач решаются методами математического программирования. Наиболее развитыми в области решения оптимизационных задач являются методы линейного программирования. Эти методы позволяют описать с достаточной точностью широкого круга задач коммерческой деятельности, таких, как планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров; распределение работников торговли должностям; организация рациональных закупок продуктов питания; распределение ресурсов; планирование капиталовложений; оптимизация межотраслевых связей; замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади; установление рационального режима работы.
В задачах линейного программирования критерий эффективности и функции в системе ограничений линейны.
Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования.
Если в задаче математического программирования имеется переменная времени, а критерий эффективности выражается через уравнения, описывающие течение операций во времени, то такая задача является задачей динамического программирования.
Во многих экономических моделях зависимости между постоянными и переменными факторами можно считать линейными.
Использование методов математического программирования в коммерческой деятельности связано со сбором необходимой информации коммерсантом, экономистом, финансистом, затем постановкой задачи вместе с математикой. Поскольку методы математического программирования уже реализованы на компьютере в виде пакета стандартных программ, то доступ к ним обычно прост, автоматизирован и не составляет особых трудностей.
Тогда эксплуатация модели включает в себя сбор и обработку информации, ввод обработанной информации в ЭВМ, расчеты на основе разработанных программ календарных планов и, наконец, выдачу результатов вычислений (в удобном для пользователей виде) для их использования в сфере производственной деятельности.
Глава Ι Линейное программирование
Дата: 2019-07-24, просмотров: 160.
