Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Задание 1 Исследование структуры совокупности

 

По исходным данным:

1. Постройте статистический ряд распределения организаций по признаку вложения в ценные бумаги, образовав пять групп с равными интервалами.

2. Постройте графики полученного распределения. Графически определите значение моды и медианы.

3. Рассчитайте характеристики ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.

4. Вычислите среднюю арифметическую по исходным данным, сравните ее с аналогичным показателем, рассчитанным в п.3 для интервального ряда распределения. Объясните причину их расхождения.

Сделайте выводы по результатам выполнения задания.

Решение:

 

Таблица 2.1 Данные значения вложений банков в ценные бумаги, млн. руб.

№ банка	вложения в ценные бумаги, млн. руб.	прибыль, млн. руб.	№ банка	вложения в ценные бумаги, млн. руб.	прибыль, млн. руб.
1	4069	110	19	9087	439
2	4279	538	20	8016	441
3	3959	85	21	7324	237
4	1032	60	22	3445	282
5	4152	39	23	2079	191
6	5347	153	24	2058	201
7	2286	215	25	648	12
8	2948	224	26	2673	77
9	2914	203	27	3145	282
10	1600	64	28	2048	451
11	2145	11	29	287	50
12	3811	153	30	2571	306
13	889	121	31	2081	440
14	584	94	32	3787	204
15	990	105	33	2131	63
16	1618	93	34	7298	650
17	1306	329	35	4729	538
18	1981	451	36	7096	175

 

1) Общая сумма вложений в ценные бумаги 116413 млн. руб.

Максимальное значение x_max = 9087

Минимальное значение x_min = 287

Размах вариации R = x_max – x_min = 9087 - 287 = 8800

Число групп по условию задачи: n= 5

Тогда величина интервала: h = R/n = 8800/5 = 1760

Получаем статистический ряд распределения банков по сумме вложений в ценные бумаги (табл.2.2).

 

Таблица 2.2 – Распределение банков по сумме вложений в ценные бумаги

Группа банков по вложениям в ценные бумаги, млн. руб.	Число банков		Накопленные частоты	общая сумма вложений в ценные бумаги
	всего	в % к итогу		Всего, млн. руб.	в % к итогу
287-2047	10	27,8%	10	15041	12,9%
2047-3807	14	38,9%	24	32205	27,7%
3807-5567	7	19,4%	31	30346	26,1%
5567-7327	3	8,3%	34	21718	18,7%
7327-9087	2	5,6%	36	17103	14,7%
итого	36	100,0%		116413	100,0%

 

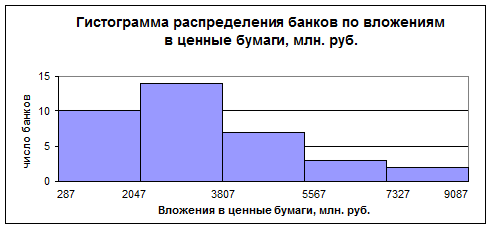
2) Графики полученного ряда распределения.

 

Гистограмма распределения

 

Кумулята распределения

 

Значение моды находится в интервале от 2047 до 3807, оно будет равно 2687.

Значение медианы находиться в интервале от 2047 до 3807, и будет равно 3053.

3) Расчет характеристик ряда распределения.

Средний размер вложений в ценные бумаги определяем по средней взвешенной:

 

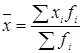
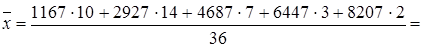3367 млн. руб.

 

Вычисление показателей вариации

- Дисперсия взвешенная

 

σ² =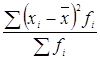  

 

Таблица 2.3 – Вспомогательная таблица для расчета дисперсии

Группы банков по сумме вложений в ценные бумаги, млн. руб.	Число банков в группе (частоты fi)	Середина интервала (xi)	(xi - )2	(xi - )2fi
287-2047	10	1167	4840000	48400000
2047-3807	14	2927	193600	2710400
3807-5567	7	4687	1742400	12196800
5567-7327	2	6447	9486400	28459200
7327-9087	3	8207	23425600	46851200
Итого	36			138617600

 

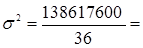3850488,889

 

- Среднее квадратическое отклонение 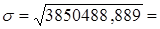1962,266

- Коэффициент вариации  = 58,279%

 

Коэффициент вариации больше 33% совокупность считается неоднородной.

Вычисление моды и медианы.

Модальная сумма вложений в ценные бумаги зависит от значения ряда с наибольшей частотой. Наибольшая частота 14 единиц наблюдается при сумме вложений 2047-3807 млн. руб.

Мо=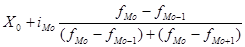

Мо= 2687

 

Медианная сумма вложений в ценные бумаги зависит от накопительной частоты, которая должна превысить половину суммарного признака. Половина суммарного признака достигается при2047-3807, и накопленная частота равна 24.

 

Ме= Ме= 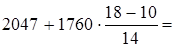3053

 

4) средняя арифметическая исходных данных равна: 116413/36 = 3233,694 млн. руб., значение больше чем среднее значение по группировке, это можно объяснить неоднородностью данной совокупности и

Выводы: Наиболее распространенной, типичной для данных банков является сумма вложений в ценные бумаги 2687 млн. руб., более половины предприятий имеют сумму вложений в ценные бумаги свыше 3053 млн. руб., при среднем уровне 3367 млн. руб. Из соотношения этих показателей ( 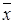>M_e >М_о) следует вывод о правосторонней асимметрии распределения числа банков по сумме вложений в ценные бумаги. Коэффициент вариации говорит о том, что данная совокупность неоднородная.

 

Задание 2 Выявление наличия корреляционной связи между признаками, установление направления связи и измерение ее тесноты

 

По исходным данным

1) установите наличие и характер связи между признаками вложение в ценные бумаги и прибыль, образовав заданное число групп с равными интервалами по обоим признакам, методами:

а) аналитической группировки,

б) корреляционной таблицей.

 

Таблица 2.4 Данные

№ банка	вложения в ценные бумаги, млн. руб.	прибыль, млн. руб.		№ банка	вложения в ценные бумаги, млн. руб.	прибыль, млн. руб.
1	4069	110		19	9087	439
2	4279	538		20	8016	441
3	3959	85		21	7324	237
4	1032	60		22	3445	282
5	4152	39		23	2079	191
6	5347	153		24	2058	201
7	2286	215		25	648	12
8	2948	224		26	2673	77
9	2914	203		27	3145	282
10	1600	64		28	2048	451
11	2145	11		29	287	50
12	3811	153		30	2571	306
13	889	121		31	2081	440
14	584	94		32	3787	204
15	990	105		33	2131	63
16	1618	93		34	7298	650
17	1306	329		35	4729	538
18	1981	451		36	7096	175
				Сумма	116413	8087

 

Решение:

А) Группировка банков по вложениям в ценные бумаги:

Максимальное значение x_max = 9087, Минимальное значение x_min = 287

Размах вариации R = x_max – x_min = 9087 – 287 = 8800

Число групп найдем по формуле Стерджесса при N = 36:

 

n=1+3,322∙Lg(36) = 1+3,322∙Lg(36) ≈ 6

 

Тогда длина интервала: h = R/n = 8800/6 = 1466,7 , округлим до 1467.

Получаются следующие группы (таблица 2.5).

 

Таблица 2.5 Интервалы группировки

	начало интервала	конец интервала
1 группа	287	1754
2 группа	1754	3221
3 группа	3221	4688
4 группа	4688	6155
5 группа	6155	7622
6 группа	7622	9087

 

Группировка банков по прибыли:

Максимальное значение x_max = 650, минимальное значение x_min = 11

Размах вариации

 

R = x_max – x_min = 650 – 11 = 639

 

Число групп найдем по формуле Стерджесса при N = 36:

 

n=1+3,322∙Lg(36) = 1+3,322∙Lg(36) ≈ 6

 

Тогда длина интервала: h = R/n = 639/6 = 106,5 , округлим до 107.

Получаются следующие группы (таблица 2.6)

Таблица 2.6 Интервалы группировки

	начало интервала	конец интервала
1 группа	11	118,0
2 группа	118,0	225,0
3 группа	225,0	332,0
4 группа	332,0	439,0
5 группа	439,0	546,0
6 группа	546,0	650,0

 

Находим число банков в каждой группе (см. приложение 1).

Для нахождения суммы вложений в ценные бумаги и прибыли в среднем на один банк по группе разделим итог по группе, соответствующего показателя, на количество банков в группе.

 

Таблица 2.7 - Итоговая групповая таблица, характеризующая структура банков по вложениям в ценные бумаги

Группа банков по вложениям в ценные бумаги	Число банков в группе	Вложения в ценные бумаги, млн. руб.		Прибыль		Удельный вес, в % к итогу по числу банков.
		всего в группе	в среднем на 1 банк	всего в группе	в среднем на 1 банк
I - [287 - 1754)	9	8954	994,889	928	103,111	25,00%
II - [1754 -3221)	13	31060	2389,231	3115	239,615	36,00%
III - [3221 - 4688)	7	27502	3928,857	1411	201,571	19,00%
IV- [4688 - 6155)	2	10076	5038,000	691	345,500	6,00%
V-[6155 - 7622)	3	21718	7239,333	1062	354,000	8,00%
VI-[7622 - 9087)	2	17103	8551,500	880	440,000	6,00%
Всего:	36	116413	3233,694	8087	224,639	100%

 

Вывод: Самая большая сумма вложений в ценные бумаги на один банк у 6 группы – 8551,5 млн. руб., хотя число предприятий в ней наименьшее - 2. Причем у этой же группы максимальная прибыль на один банк. Максимальное число банков во второй группе.

Сравнивая графы 4 и 6 таблицы 2.7, замечаем, что с увеличением вложений в ценные бумаги увеличивается и прибыль, то есть между изучаемыми признаками существует прямая зависимость.

По второму признаку – прибыль группировка:

 

Таблица 2.8 - Итоговая групповая таблица, характеризующая структура банков по прибыли

Группа банков по прибыли, млн. руб.	Число банков в группе	вложения в ценные бумаги, млн. руб.		Удельный вес, в % к итогу	прибыль, млн. руб.
		всего в группе	в среднем на 1 банк		всего в группе	в среднем на 1 банк
I - [11 - 118)	13	25888	1991,385	36,00%	863	66,385
II - [118 - 225)	10	33215	3321,500	28,00%	1840	184,000
III - [225 - 332)	5	17791	3558,200	14,00%	1436	287,200
IV- [332 - 439)	0	-	-	0,00%	-	-
V-[439 - 546)	7	32221	4603,000	19,00%	3298	471,143
VI-[546 - 650)	1	7298	7298,000	3,00%	650	650,000
Всего:	36	116413	3233,694	100%	8087	224,639

 

Вывод: Наибольший удельный вес по данной группе банков 36%, составляют банки с прибылью от 11 до 118 млн. руб. Наименьший удельный вес по данной группе предприятий 3%, составляют банки с прибылью от 546 до 650 млн. руб. Банков с прибылью от 332 до 439 млн. руб. нет.

Самое большая сумма вложений в ценные бумаги на 1 банк у 6 группы – 7298 млн. руб., и число банков в ней наименьшее -1. Максимальное число банков в первой и во второй группах, составляет 64% от всех банков. Максимальная прибыль в среднем на 1 банк у 6 группы – 650 млн. руб., хотя эта группа предприятий составляет лишь 3%.

 

Таблица 2.9 Анализ наличия связи между признаками

Групп банков по факторному признаку (вложения в ценные бумаги)		Группы банков по результативному признаку  (прибыль)
		I – [11 - 118)	II – [118 - 225)	III – [225 - 332)	IV- [332 - 439)	V- [439 - 546)	VI- [546 - 650)	итого
группа	№ банка	1,3,4,5,10,11,14, 15,16,25,26,29, 33	6,7,8,9,12,13, 23,24,32,36	17,21,22,27, 30	-	2,18,19,20, 28,31,35	34
I - [287 - 1754)	4,10,13, 14,15,16, 17,25,29	7	1	1				9
II - [1754 -3221)	7,8,9,11, 18,23,24, 26,27,28, 30,31,33	3	5	2		3		13
III - [3221 - 4688)	1,2,3,5, 12,22,32	3	2	1		1		7
IV- [4688 - 6155)	6,35		1			1		2
V-[6155 - 7622)	21,34,36		1	1			1	3
VI-[7622 - 9087)	19,20					2		2
Всего:		13	10	5	0	7	1

 

Вывод: Связь между факторным признаком (вложения в ценные бумаги) и результативным (прибыль) прямая, т.к. данные в таблице 2.9 располагаются вдоль диагонали направленной из левого верхнего угла в правый нижний угол.

Б) Метод Корреляционной таблицы

Связь между признаками прямая. Построив точечную диаграмму по данным, где факторным признаком будет сумма вложений в ценные бумаги, а результативным прибыль добавляем линию тренда. Получаем уравнение прямой зависимости:

Уравнение прямой имеет вид:

 

y = 0,0367x + 105,81

 

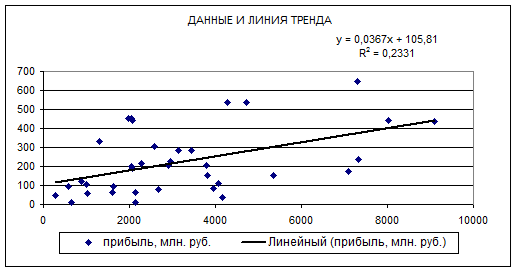
Строим таблицу для расчета коэффициента корреляции.

 

Таблица 2.10 Расчеты для коэффициента корреляции

№ банка	вложения в ценные бумаги, млн. руб. Х	прибыль, млн. руб. У	Х2	ХУ	У2
1	4069	110	16556761	447590	12100
2	4279	538	18309841	2302102	289444
3	3959	85	15673681	336515	7225
4	1032	60	1065024	61920	3600
5	4152	39	17239104	161928	1521
6	5347	153	28590409	818091	23409
7	2286	215	5225796	491490	46225
8	2948	224	8690704	660352	50176
9	2914	203	8491396	591542	41209
10	1600	64	2560000	102400	4096
11	2145	11	4601025	23595	121
12	3811	153	14523721	583083	23409
13	889	121	790321	107569	14641
14	584	94	341056	54896	8836
15	990	105	980100	103950	11025
16	1618	93	2617924	150474	8649
17	1306	329	1705636	429674	108241
18	1981	451	3924361	893431	203401
19	9087	439	82573569	3989193	192721
20	8016	441	64256256	3535056	194481
21	7324	237	53640976	1735788	56169
22	3445	282	11868025	971490	79524
23	2079	191	4322241	397089	36481
24	2058	201	4235364	413658	40401
25	648	12	419904	7776	144
26	2673	77	7144929	205821	5929
27	3145	282	9891025	886890	79524
28	2048	451	4194304	923648	203401
29	287	50	82369	14350	2500
30	2571	306	6610041	786726	93636
31	2081	440	4330561	915640	193600
32	3787	204	14341369	772548	41616
33	2131	63	4541161	134253	3969
34	7298	650	53260804	4743700	422500
35	4729	538	22363441	2544202	289444
36	7096	175	50353216	1241800	30625
Итого	116413	8087	550316415	32540230	2823993
Среднее	3233,694	224,639	15286567,08	903895,278	78444,25

 

Для проверки тесноты связи между признаками находим коэффициент корреляции:

 

,

 

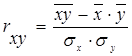где

 

, , , ,

 

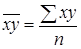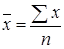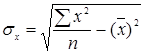Получаем следующие значения:

 

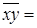903895,278, 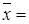3233,694, 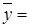224,639

2197,678, 167,277

 

Коэффициент корреляции:

 

 0,48278

 

Т.к. коэффициент больше 0,3 но меньше 0,5 то связь слабая, прибыль зависит от суммы вложений только на 48,3%.

Коэффициент положителен это означает, что при росте значения Х значение У также увеличивается. Связь прямая.

Коэффициент детерминации: Д= r²*100%, Д=23,3%

Полученное уравнение y = 0,0367x + 105,81, на 23,30% объясняет общий разброс результатов наблюдений.

 

Задание 3. Ошибки выборки

 

По результатам выполнения задания 1 с вероятностью 0,954 определите:

1) Ошибку выборки средней величины вложения средств банками в ценные бумаги и границы, в которых будет находиться средняя величина вложений в генеральной совокупности.

2) Ошибку выборки доли банков с вложениями средств в ценные бумаги 3811 млн. руб. и более и границы, в которых будет находиться генеральная доля.

Решение

1) Предельная ошибка выборки для средней:

 

 

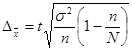
Выборка механическая 3%. Значит, n=3, N=100, с вероятностью 0,954.

Для вероятности 0, 954 по интегральной функции Лапласа t=1,99.

Дисперсия - 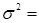3850488,889, среднее значение вложений в ценные бумаги 3367 млн. руб.

 

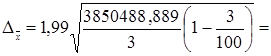2220,426

 

Возможные пределы, в которых ожидается средняя величина вложений в ценные бумаги в генеральной совокупности:

 

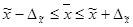
3367-2220,426 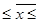 3367+2220,426

1146,574 5587,426

 

С вероятностью 0,954 можно утверждать, что средний размер вложений в ценные бумаги для всех банков находится в пределах от 1146,574 млн. руб. до 5587,426 млн. руб.

2) Всего число банков n=36.

Число банков с вложениями средств в ценные бумаги 3811 млн. руб. и более - 12, тогда точечная оценка W=12/36=1/3=0,333.

Средняя ошибка выборки:

 

М_w= 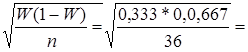0,079

 

t=2 по таблице Стьюдента.

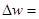M_wt=2*0,079=0,158

 

Получаем интервал от 0,333 - 0,158 до 0,333 + 0,158, т.е. от 0,175 до 0,491.

Следовательно, ошибка выборки доли банков с вложениями средств в ценные бумаги 3811 млн. руб. и более равна 7,9%. Границы, в которых будет находиться генеральная: от 17,5% до 49,1%.

 

Задание 4. Анализ ряда динамики

 

Имеются следующие данные по коммерческому банку о просроченной задолженности по кредитным ссудам:

 

Таблица 2.11 Данные

год	задолженность по кредиту, млн. руб.	по сравнению с предыдущим годом			абсолютное значение 1% прироста, млн. руб.
		абсолютный прирост, млн. руб.	темп роста, %	темп прироста, %
2000		-	-	-	-
2001			106,25%		16
2002		100
2003				30,00%
2004			108,50%

 

Определите:

1) Задолженность по кредиту за каждый год.

2) Недостающие показатели анализа ряда динамики и внесите их в таблицу.

3) Основную тенденцию развития методом аналитического выравнивания.

Осуществите прогноз задолженности на следующие два года на основе найденного тренда. Постройте графики. Сделайте выводы.

Решение:

1-2) Пусть y_t –задолженность по кредиту в период t, тогда

Абсолютный прирост: y_t – y_t-1,

Темп роста: y_t/y_t-1,

Темп прироста: y_t/y_t-1 – 1.

Абсолютное значение одного процента прироста, определяется как отношение абсолютного прироста к соответствующему темпу прироста:

 

 

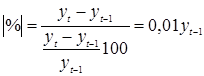
Тогда по абсолютному значению 1% прироста 2001 года, находим задолженность по кредиту 2000 года:

 

16= 0,01*у_t-1,

 

у_t-1 = 1600 млн. руб.

Значение темпа прироста: 106,25% – 1 = 6,25%.,

Задолженность по кредиту за 2001г.: 1600*106,25% = 1700 млн. руб., абсолютный прирост составит: 1700-1600 = 100 млн. руб.

Далее находим показатели 2002 года:

Задолженность по кредиту: 1700 + 100 = 1800 млн. руб.

Темп роста: 1800/1700 = 105,88%, темп прироста составит 105,88% - 1 = 5,88%, абсолютное значение 1% прироста 0,01*1700 = 17 млн. руб.

Показатели по кредитной задолженности 2003 года:

Темп роста 1+30% = 130%

Задолженность по кредиту 1800 * 130% = 2340 млн. руб.

Абсолютный прирост 2340 – 1800 = 540 млн. руб.

Абсолютное значение 1% прироста: 0,01*1800 = 18 млн. руб.

Показатели по кредитной задолженности 2004 года:

Темп прироста 108,5% - 1 = 8,5%

Задолженность по кредиту 2340 * 108,5% = 2538,9 млн. руб.

Абсолютный прирост 2538,9 – 2340 = 198,9 млн. руб.

Абсолютное значение 1% прироста: 0,01*2340 = 23,4 млн. руб.

В результате манипуляций получим таблицу 2.12

 

Таблица 2.12 Просроченная задолженность по кредитным ссудам.

год	задолженность по кредиту, млн. руб.	по сравнению с предыдущим годом			абсолютное значение 1% прироста, млн. руб.
		абсолютный прирост, млн. руб.	темп роста, %	темп прироста, %
2000	1600	-	-	-	-
2001	1700	100	106,25%	6,25%	16
2002	1800	100	105,88%	5,88%	17
2003	2340	540	130,00%	30,00%	18
2004	2538,9	198,9	108,50%	8,50%	23,4

 

3) Тенденция развития методом аналитического выравнивания.

Построим график задолженности по кредиту, млн. руб.

 

 

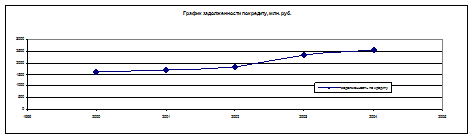
По графику модно предположить линейную зависимость задолженности по кредиту от года.

Определяем параметры линейного уравнения:

 

У=а₀ + а₁Х

Для этого найдем а₁ и а₀ из системы:

 

,

 

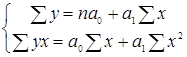Для нахождения коэффициентов системы оставим дополнительную таблицу.

 

Таблица 2.13 Расчет коэффициентов системы уравнений.

№ п/п	Год (Х)	задолженность по кредиту (У)	Х2	ХУ	У2	У расчетное
1	2000	1600	4000000	3200000	2560000	1492,22
2	2001	1700	4004001	3401700	2890000	1744,00
3	2002	1800	4008004	3603600	3240000	1995,78
4	2003	2340	4012009	4687020	5475600	2247,56
5	2004	2538,9	4016016	5087955	6446013,21	2499,34
Итого	10010	9978,9	20040030	19980275,6	20611613,21	9978,9
Среднее	2002	1995,78	4008006	3996055,12	4122322,642	1995,78

 

Имеем следующую систему:

 

 

Находим решение методом Крамара:

Δ=	5	10010	= 5∙20040030 – 10010∙10010 = 50
	10010	20040030
Δ0 =	9978,9	10010	= 9978,9∙20040030 – 10010∙19980275,6 = 25103289
	19980275,6	20040030
Δ1 =	5	9978,9	=5∙19980275,6 – 9978,9∙10010 = 12589
	10010	19980275,6

 

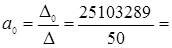-502067,78 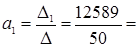251,78

 

Уравнение регрессии имеет вид:

 

 

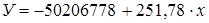
Расчетные значения результативного признака (выпуска продукции) представлены в таблице 2.13.

Находим остаточную сумму квадратов и среднюю ошибку аппроксимации.

Для проверки тесноты связи между признаками находим коэффициент корреляции:

 

,

 

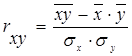где

 

, , , ,

 

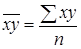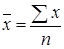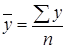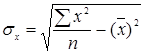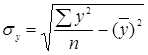
Получаем следующие значения:

 

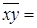3996055,1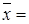2, 2002, 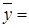1995,78

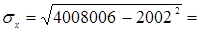1,414

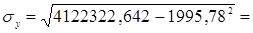373,075

 

Коэффициент корреляции:

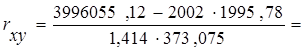0,954565

 

Т.к. коэффициент больше 0,7 то связь сильная. Задолженность по кредиту зависит от года на 95,046%

Коэффициент положителен это означает, что при росте значения Х значение У также увеличивается. Связь прямая.

Коэффициент детерминации: Д= r²*100%, Д=91,12%

 

 

Прогноз задолженности на основе найденного тренда:

 

2005 год: 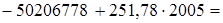2751,12 млн. руб.

2006 год: 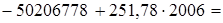3002,9 млн. руб.

 

Вывод: Найденная зависимость указывает на линейный рост задолженности по кредиты с каждым последующим годом.

Используя средства Excel, построим для сравнения тренд экспоненциальный.

 

 

Полученная зависимость имеет коэффициент детерминации больше чем линейная, следовательно, она описывает тенденцию кредитной задолженности лучше.