Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Система уравнений называется неоднородной, если хотя бы один свободный член уравнения не равен нулю.

Если главный определитель системы n уравнений с n неизвестными не равен нулю, то система имеет единственное решение, корни которого определяются по формулам:

 

, , …,

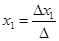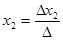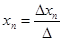
4. Дайте определение матрицы и ее размера. Приведите пример матриц размеров: 1х3, 3х4,1х1.

 

Матрицей называется таблица чисел или каких-либо других элементов, содержащая m строк и n столбцов.

 

Общий вид матрицы

 

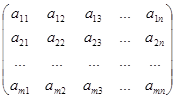
Матрица имеет размер, который определяется ее количеством строк и столбцов, что записывается так – А _{m ´ n}.

Например, числовая матрица размером 1´1 имеет вид 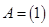, размером 1´3 имеет вид 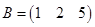, размером 3´4 имеет вид .

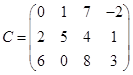5. Что такое союзная или присоединенная матрица? Приведите пример вычисления союзной матрицы для заданной.

 

Если для заданной квадратной матрицы А определить алгебраические дополнения всех ее элементов и затем транспонировать их, то полученная таким образом матрица будет называться союзной или присоединенной по отношению к матрице А и обозначаться символом Ã

Для матрицы 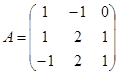 найти Ã.

 

Составляем определитель матрицы А

 

 

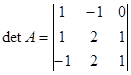
Определяем алгебраические дополнения всех элементов определителя по формуле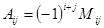

 

; ;

.

; ;

.

; ;

.

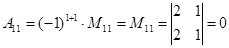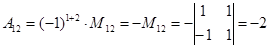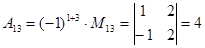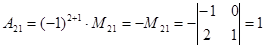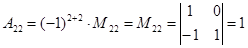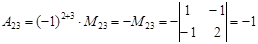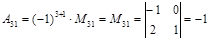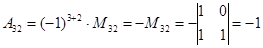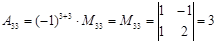Транспонируя полученные алгебраические дополнения, получаем союзную или присоединенную матрицу Ã по отношению заданной матрицы А.

 

6. Вычислить определитель 3‑го порядка, разложив его по 1‑й строке

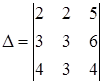
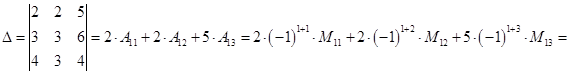
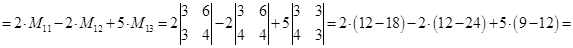
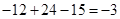
7. Определить алгебраические дополнения элементов 2‑й строки определителя 3-го порядка

 

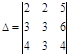
Для элемента а₂₁ i=2, j=1 и i+j=3 число нечетное, отсюда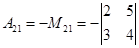

Для элемента а₂₂ i=2, j=2 и i+j=4 число четное, отсюда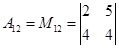

Для элемента а₂₃ i=2, j=3 и i+j=5 число нечетное, отсюда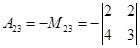

Найти решение системы уравнений методом Крамера

 

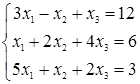
Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при X_{1 - n} не будет равен нулю. Обозначим этот определитель знаком – Δ. Если этот определитель не равен нулю, то решаем дальше. Тогда каждый X_i = Δ_i / Δ, где Δ_i – это определитель составленный из коэффициентов при X_{1 - n}, только значения коэффициентов в i – ом стольбце заменены на значения за знаком равенства в сисетеме уравнений, а Δ – это главный определитель

Решение

Запишем систему в виде:

 

 

Главный определить

 

 

Выполните операцию произведения двух матриц АхВ

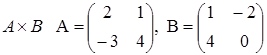
Решение

 

Найти матрицу |C| = |A| x |B|

Вычислим элементы матрицы |C|:

 

c_1,1 = a_1,1b_1,1+a_1,2b_2,1

c_1,2 = a_1,1b_1,2+a_1,2b_2,2

c_2,1 = a_2,1b_1,1+a_2,2b_2,1

c_2,2 = a_2,1b_1,2+a_2,2b_2,2

c1,1 =		2			*			1					+			1			*			4				=				2				+			4				=				6
c1,2 =		2			*				-2			+				1			*				0				=				-4			+				0				=				-4
c2,1 =	-3		*			1				+				4			*			4				=				-3				+			16				=				13
c2,2 =		-3		*			-2				+				4			*			0				=				6				+			0				=				6

Результирующая матрица |С|:

 

6	-4
13	6

 

10. Какие величины называются скалярными и векторными? Приведите примеры скалярных и векторных величин? Каково условие равенства векторов? Приведите пример сложения двух векторов по правилу параллелограмма и треугольника

Скалярной величиной или просто скаляром называется величина, которая при определённом выборе единицы измерения определяется числом (удельный вес, плотность, работа, мощность, температура и т.д.)

Вектор – направленный отрезок, имеющий определённую величину (скорость, ускорение, сила, напряженность магнитного и электрического поля и т.д.).

Скалярная величина – 10 минут, векторная – 100 км/ч.

Два вектора 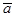 и 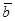 равны, если они равнонаправлены и имеют один и тот же модуль.

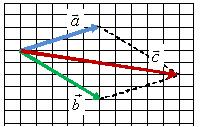
Правило треугольника

Для того чтобы сложить два вектора 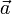и 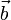нужно переместить вектор 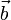параллельно самому себе (рис. 1, б) так, чтобы его начало (точка B на рис. 1, а) совпадало с концом вектора 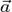(точка A на рис. 1, а). Тогда их суммой будет вектор 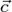(рис. 1, г), начало которого совпадает с началом вектора 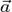(точка D на рис. 1, в), а конец – с концом вектора 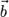(точка C на рис. 1, в).

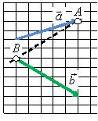
а б

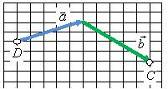
в г

Рис. 1.

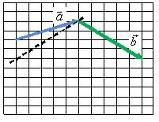
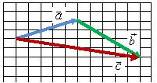
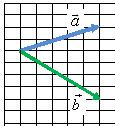
Правило параллелограмма

Для того чтобы сложить два вектора 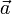и 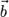нужно переместить их параллельно самим себе так, чтобы начала векторов 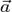и 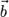находились в одной точке (рис. 2, а). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 2, б). Тогда их суммой будет вектор 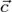(рис. 2, в), начало которого совпадает с общим началом векторов (точка A на рис. 2, б), а конец – с противоположной вершиной параллелограмма (точка В на рис. 2, б).

 

а

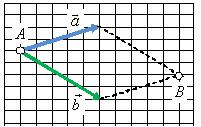
б в

Рис. 2.