Смешанное соединение резисторов представляет собой комбинацию последовательного и параллельного соединений. На рис.18а показан пример смешанного соединения. В этой схеме резисторы R2 и R3 соединены параллельно. Последовательно с этими резисторами подключён резистор R1.

    При решении задач на смешанное соединение требуется прежде всего, провести анализ схемы. Необходимо нарисовать схему, обозначить все её элементы, а также токи и напряжения, действующие в схеме. Следует мысленно выделить на схеме элементы соединенные параллельно или последовательно и затем, поэтапно, упростить схему.

На рис.18а показана исходная схема, а затем этапы её упрощения на рис.18б и 18в. Заметьте, что номера токов и напряжений, обозначенных на схеме, всегда совпадают с номером соответствующего сопротивления.

Прежде всего, проведено объединение параллельно соединённых резисторов R₂ и R₃ в одно сопротивление R_2,3. В результате, схема приобрела вид, показанный на рис.18б. На этой схеме видно, что сопротивления R₁ и R_2,3 соединены последовательно.

Объединяя сопротивления R₁ и R_2,3, получим общее сопротивление, что показано на рис.18в.

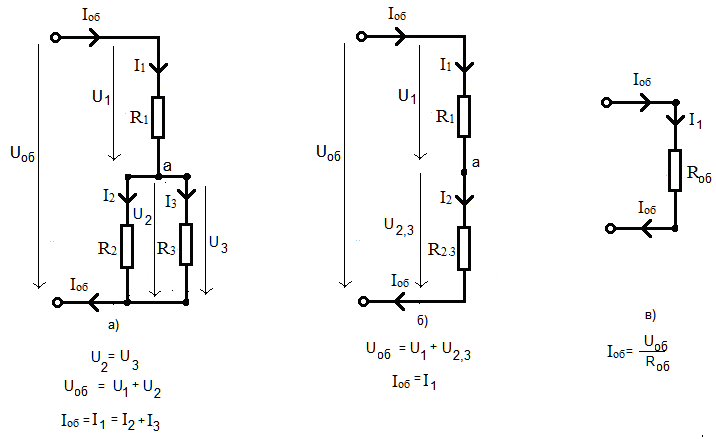
Рис. 18. Смешанное соединение резисторов: а) исходная схема; б) и в) схемы после упрощения

    Далее нужно проанализировать схему, рассмотреть, как в ней протекает ток. На схеме, показанной на рис.18а общий для всей схемы ток Iоб, протекая от верхней клеммы, через резистор R₁, где он же обозначен как I₁, доходит до узла а (см. рис. 18а).

    В узле а ток разделяется на две ветви. По первому закону Кирхгофа I₁ равен сумме токов I₂+I₃. Далее эти токи вновь сливаются в общий ток Iоб, который идёт к нижней клемме. Напряжения на параллельно соединённых резисторах R₂ и R₃ одинаковы.

    В схеме на рис. 18б всё уже проще. Видно, что резисторы R₁ и R_2,3 соединены последовательно. Через всю цепь ток, одинаковый во обоих сопротивлениях. Общее напряжение, приложенное к цепи, равно сумме напряжений на резисторах R₁ и R_2,3.

    Совсем просто выглядит схема на рис. 18в. В этой схеме только одно сопротивление.

    После упрощения схемы следует записать под каждой из них соотношения для токов и напряжений, используя свойства последовательного и параллельного соединения. Такая запись показана на рис.18. Начинать запись соотношений следует с самой простой схемы, т.е. с рис.18в.

    После проведения анализа схемы и её упрощения можно приступать к решению задачи на смешанное соединение? Руководствуясь записанными выше соотношениями для каждой схемы.

Пример 9. Расчёт цепи со смешанным соединением резисторов

Для схемы, показанной на рис.18 известно общее напряжение, равное 120В

Известна величина каждого сопротивления: R₁=16Ом, R₂=40Ом и R₃=60Ом. Найти: общее сопротивление схемы, все токи и напряжения, обозначенные на схеме.

Решение:

1. Найдём общее сопротивление цепи:

1.1. Общее сопротивление резисторов R₂ и R₃:

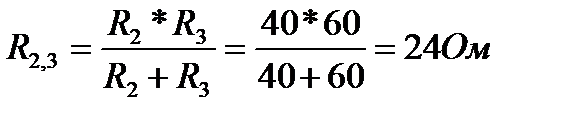
1.2. Общее сопротивление всей цепи:

R_об= R₁+R_2,3=16+24=40Ом

2. Находим общий ток, потребляемый схемой:

I_об=U_об/ R_об=120/40=3А= I₁

3. Определяем напряжение на резисторе R₁:

U₁= I₁• R₁=3*16=48В

4. Найдём напряжение на параллельно включённых резисторах R₂ и R₃:

U_2,3= U_об - U₁ = 120 - 48 =72В = U₂= U₃

5. Найдем токи в резисторах R₂ и R₃:

I₂= U₂/ R₂= 72/40 = 1,8А

I₃= U₃/ R₃= 72/60 = 1,2А

Сложная электрическая цепь

Сложной называется цепь, состоящая из нескольких контуров, и содержащая несколько источников ЭДС. Пример сложной цепи показан на рис. 19. Цепь содержит два источника ЭДС и несколько резисторов. В схеме можно выделить несколько контуров.

Перед началом рассмотрения данной темы необходимо повторить свойства параллельного соединения резисторов.

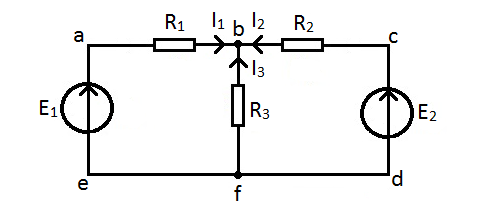
Рис. 19. Сложная электрическая цепь

Контуром называется любой замкнутый участок электрической цепи. В данной схеме можно выделить три контура: контур a, b, f, e, a, контур b, c, d, f, b и контур: a, c, d, e, а.

Расчет сложных цепей ведется с применением первого и второго законов Кирхгофа. Первый закон Кирхгофа был рассмотрен при изучении параллельного соединения резисторов. Второй закон Кирхгофа гласит: алгебраическая сумма ЭДС, входящих в контур равна алгебраической сумме падения напряжения на элементах этого контура.

Обычно, требуется найти значения токов во всех ветвях, если известны значения ЭДС всех источников и величина всех сопротивлений.

Для решения этой задачи требуется составить и решить систему уравнений. Число уравнений, входящих в систему, равно числу неизвестных токов. Для рассматриваемой схемы потребуется три уравнения, т.к. в схеме три ветви и, соответственно три тока, которые нужно найти.

Расчет сложных цепей производится по определенному алгоритму:

1. Прежде всего, произвольно обозначаем направление токов в ветвях (см. рис. 19). Мы пока не знаем, в какую сторону направлены токи, обозначаем направление токов наугад. Позже, решение задачи укажет нам на ошибку, если она допущена.

2. По первому закону Кирхгофа составляем (n-1) уравнений, где n – число узлов. В нашей схеме два узла: это точки b и f. Для узла b, по первому закону Кирхгофа, запишем: 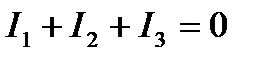, т.к. все три тока направлены к узлу b. (На самом деле такой вариант невозможен. Не может быть, чтобы были токи, подходящие к узлу и не было токов, отходящих от узла. Но сейчас это не имеет значения.)

3. Всего нужно составить 3 уравнения (по числу неизвестных токов). Недостающие уравнения составим по второму закону Кирхгофа для двух любых контуров. Предварительно договоримся, что обход по контуру при составлении уравнения будем совершать по часовой стрелке. Термин обход по контуру следует понимать так: Выбираем на контуре любую точку и начинаем двигаться вдоль контура. "По дороге" записываем встречающиеся на пути ЭДС (Е) и напряжения на резисторах.

    ЭДС входит в уравнение с плюсом, если направление стрелки источника совпадает с направлением обхода по контуру. В противном случае запишем его со знаком "минус".

    Падение напряжения на сопротивлении (U=I•R) входит в уравнение с плюсом, если направление тока в резисторе совпадает с направлением обхода.

    Для контура a, b, f, e, a, запишем:

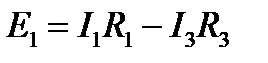
    Для контура b, c, d, f, b:

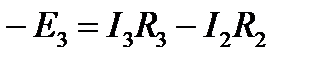
4) Объединяя составленные нами уравнения, получим систему уравнений:

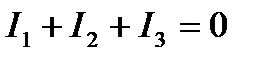
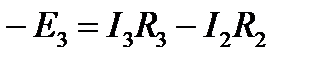
5) Теперь дело за малым. В систему уравнений нужно подставить известные из условия задачи величины и решить систему относительно токов. Будут получены числовые значения токов.

    Если ток получается со знаком "минус", значит, мы неправильно указали его направление и, на самом деле, он протекает в направлении, противоположном, указанному на рис.19.

    Чем сложнее схема, тем больше уравнений в системе и тем сложнее ее решить.