«Задача – это такая ситуация, которая связана с числами и требует выполнения арифметических действий над ними» [1, 171].
«Текстовая задача – это словесная модель некоторого явления (ситуации, процесса). Чтобы решить такую задачу, надо перевести ее на язык математических действий, то есть построить ее математическую модель.
Решение любой задачи – процесс сложной умственной деятельности. Реальные объекты и процессы в задаче бывают столь многогранны и сложны, что лучшим способом их изучения часто является построение и исследование модели как мощного орудия познания.» [4, 5]
Решению текстовых задач в обучении уделяется огромное внимание. Связано это с тем, что такие задачи часто являются не только средством формирования многих математических понятий, но и главное - средством формирования умений строить математические модели реальных явлений, а также средством развития мышления детей. Существуют различные методические подходы к обучению детей решению текстовых задач. Но какую бы методику обучения ни выбрал учитель, ему надо знать, как построены такие задачи.
«Любая текстовая задача представляет собой описание какого-либо явления (ситуации, процесса). С этой точки зрения текстовая задача есть словесная модель явления (ситуации, процесса). И, как во всякой модели, в текстовой задаче описывается не все явление в целом, а лишь некоторые его стороны, главным образом, его количественные характеристики.» [22, 121]
Обобщая, можно сказать, что текстовая задача есть описание на естественном языке некоторого явления (ситуации, процесса) с требованием дать количественную характеристику какого-либо компонента этого явления, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения.
Утверждения задачи называют условиями. В задаче обычно не одно условие, а несколько элементарных условий. Они представляют собой количественные или качественные характеристики объектов задачи и отношений между ними. Требований в задаче может быть несколько. Они могут быть сформулированы как в вопросительной, так и утвердительной форме. Условия и требования взаимосвязаны. Систему взаимосвязанных условий и требований называют высказывательной моделью задачи. Таким образом, чтобы понять, какова структура задачи, надо выявить ее условия и требования, отбросив все лишнее, второстепенное, не влияющее на ее структуру. Иными словами, надо построить высказывательную модель задачи. Чтобы получить эту модель, надо текст задачи развернуть (сделать это можно письменно или устно), так как текст задачи, как правило, дается в сокращенном, свернутом виде. Для этого можно перефразировать задачу, построить ее графическую модель, ввести какие-либо обозначения и т.д.
«Основными методами решения текстовых задач являются арифметический и алгебраический.
Решить задачу арифметическим методом - это значит найти ответ на требование задачи посредством выполнения арифметических действий над числами.
Одну и ту же задачу можно решить различными арифметическими способами. Они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи» [16, 374].
Решить задачу алгебраическим методом - это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. Если для одной и той же задачи можно составить различные уравнения (системы уравнений), то это означает, что данную задачу можно решить различными алгебраическими способами.
Решение любой задачи - процесс сложной умственной деятельности. Чтобы овладеть им, надо знать основные этапы решения задачи и некоторые приемы их выполнения.
Деятельность по решению задачи арифметическим методом включает следующие основные этапы:
1. Анализ задачи.
2. Поиск плана решения задачи.
3. Осуществление плана решения задачи.
4. Проверка решения задачи.
В реальном процессе решения задачи названные этапы не имеют четких границ и не всегда выполняются одинаково полно. Все зависит от уровня знаний и умений решающего.
Анализ задачи
Основное назначение этого этапа - понять в целом ситуацию, описанную в задаче; выделить условия и требования; назвать известные и искомые объекты, выделить все отношения (зависимости) между ними. Производя анализ задачи, вычленяя ее условия, мы должны соотносить этот анализ с требованиями задачи.
И таблица, и схематический чертеж являются вспомогательными моделями задачи. Они служат формой фиксации анализа текстовой задачи и являются основным средством поиска плана ее решения.
После построения вспомогательной модели необходимо проверить:
1) все ли объекты задачи показаны на модели;
2) все ли отношения между объектами отражены;
3) все ли числовые данные приведены;
4) есть ли вопрос (требование) и правильно ли он указывает искомое?
2. Поиск и составление плана решения задачи
Назначение этого этапа: установить связь между данными и исходными объектами, наметить последовательность действий. План решения задачи - это лишь идея решения, его замысел.
Поиск плана решения задачи является трудным процессом. Одним из наиболее известных приемов поиска плана решения задачи арифметическим способом является разбор задачи по тексту или по ее вспомогательной модели.
Разбор задачи проводится в виде цепочки рассуждений, которая может начинаться от данных задачи, так и от ее вопросов.
3. Осуществление плана решения задачи
Назначение данного этапа – найти ответ на требование задачи, выполнив все действия в соответствии с планом.
Для текстовых задач, решаемых арифметическим способом, используются следующие приемы:
- запись по действиям; (с пояснением, без пояснения, с вопросами)
- запись в виде выражения.
Проверка решения задачи
Назначение данного этапа – установить правильность или ошибочность выполнения решения.
Известно несколько приемов, помогающих установить, верно ли решена задача:
1. Установление соответствия между результатом и условиями задачи.
Для этого найденный результат вводится в текст задачи и на основе рассуждений устанавливается, не возникает ли при этом противоречия.
2. Решение задачи другим способом.
Подробнее остановимся на моделировании и использовании этого метода при работе над текстовой задачей.
Обучение с применением моделирования повышает активность мыслительной деятельности учащихся, помогает понять задачу, самостоятельно найти рациональный путь решения, установить нужный способ проверки, определить условия, при которых задача имеет или не имеет решение. Модель дает возможность более полно увидеть зависимость между данными и искомыми в задаче, представить задачу в целом, помогает обобщить теоретические знания. Постановка учебной задачи составляет мотивационно–ориентировочное звено – первое звено учебной деятельности. Вторым (центральным) звеном учебной деятельности является исполнительское, то есть следующие учебные действия для решения учебной задачи:
1) преобразование условий предметной задачи с целью выявления в ней основного отношения;
2) моделирование выделенного в ней отношения в предметной, графической или буквенной форме;
3) преобразование модели отношения для изучения его свойств;
4) построение системы частных задач, решаемых общим способом.
«Чтобы научить школьников самостоятельно и творчески учиться, нужно включать их в специально организованную деятельность, сделать хозяевами этой деятельности. Одним из способов включения учащихся в активную деятельность в процессе решения задач и является моделирование.
Умение решать задачи – один из основных показателей уровня математического развития, глубины усвоения учебного материала» [11, 28].
«Одна из основных причин допускаемых ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа, которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее графического моделирования» [8, 16].
В 5 классе, как правило, в процессе анализа используются разные виды краткой записи или готовые схемы, а создание модели задачи на глазах учеников или самими учащимися в процессе решения задач используется крайне редко. Учителя при фронтальном анализе и решении задачи нередко ограничиваются правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания.
«Для устранения отмеченных недостатков следует, прежде всего, решительно улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися» [1, 174]. Главное для каждого ученика на этом этапе – понять задачу, то есть уяснить, о чем эта задача, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми и т.п. Для этого, где возможно, следует применять метод моделирования ситуации, отраженной в задаче.
«Используемый в науке метод моделирования заключается в том, что для исследования какого-либо явления или объекта выбирают или строят другой объект, в каком-то отношении подобный исследуемому; построенный или выбранный объект изучают и с его помощью решают исследовательские задачи, а затем результат решения этих задач переносят на первоначальное явление или объект.» [21, 156]
В 5 классе, анализируя задачу № 59: [3, 19]
«Длина Волги 3530 км Днепр на 1330 км короче Волги, а Урал длиннее Днепра на 228 км. Какова длина реки Урал?», обычно записывают ее кратко примерно так:
длина Волги – 3530 км;
длина Днепра - ?, на 1330 км короче Волги;
длина Урала - ?, на 228 км длиннее Днепра.
Такая запись при первичном анализе задачи нерациональная, так как не раскрывает наглядно взаимодействия между данными и искомыми, не помогает в выборе действия.
Учащимся предлагается смоделировать условие задачи следующим образом:
|
длина Волги –
1330 км
длина Днепра –
228 км
длина Урала –
?
Эта модель дает наглядное представление об отношениях между данными и искомыми в задачах.
Анализируя задачу, учащиеся выясняют, что Днепр на 1330 км короче Волги, то есть столько же, но без 1330; поэтому отрезок на схеме, изображающий длину Днепра, они начертят короче отрезка, показывающего длину Волги. А так как Урал длиннее Днепра на 228 км, то есть столько же и еще 228; то и отрезок, показывающий длину Урала, должен быть длиннее отрезка, показывающего длину Днепра.
Рассмотрим, как можно смоделировать задачу № 468: [3, 106]
«На мельницу привезли 9600 кг пшеницы. При размоле отходы составили 1200 кг. Муку насыпали в мешки и погрузили на 3 машины. На первую погрузили – 30 мешков, на вторую – 35 мешков, а на третью – 40 мешков. Сколько килограммов муки погрузили на первую машину, если во всех мешках муки было поровну?»
В процессе разбора этой задачи с учащимися, получаем примерно такие
вспомогательные модели:
|
|
Осталось?
9600 кг
30 мешков
1-ая машина:
| |
|
2-ая машина:
|
3-ья машина:
Такая модель помогает уяснить одно из важных условий задачи, которое вызвало наибольшее затруднение в решении, а именно: после того, как муку насыпали в мешки, во всех мешках муки стало поровну.
Модель создает предпосылки активной мыслительной деятельности в поисках разных способов решения одной и той же задачи.
Рассмотрим еще одну задачу и модель к ней.
Задача 1318: [3, 290]
«Для посева было приготовлено 25,2 т семян. В первый день на посев израсходовали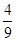 
всех семян, а во второй 
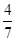остатка. Сколько семян осталось после двух дней посева?»
По предложению учеников «весь посев» изобразим в виде прямоугольника. На схематическом чертеже отметим данные и установим, что будем определять. Получится такая схема:
|
|
|
| ? |
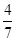
25,2 т
Схема помогает ученикам самостоятельно найти правильные решения данной задачи.
«Иногда в 5 классе задачу не проверяют или понимают под проверкой, например, прочтение способа решения задачи для всего класса или сверку на доске. Модель не только поможет найти рациональный способ решения задачи, но и поможет проверить его правильность.» [27, 23]
Условие задачи с пропорциональными величинами обычно кратко записывают в таблицу. Например, следующим образом.
Задача 411: [3, 97]
«Привезли 12 ящиков яблок по 30 кг в каждом и 8 ящиков груш по 40 кг в каждом. Какова масса всех фруктов?»
| Масса одного ящика | Количество ящиков | Общая масса |
| 30 кг | 12 ящ. | ? |
| 40 кг | 8 ящ. |
«Таблица – это тоже модель задачи, но более абстрактная, чем схематический рисунок или чертеж. Она предполагает уже хорошее знание учащимися взаимозависимостей пропорциональных величин, так как сама таблица этих взаимозависимостей не показывает. Поэтому при первичном знакомстве с такой задачей таблица мало помогает представить математическую ситуацию и выбрать нужное действие» [26, 127].
При первичном знакомстве с таким видом задач целесообразно смоделировать условие в виде схематического рисунка или чертежа.
|
|
? ?
|
?
По такой модели решение задачи становится более понятным для всех учащихся.
Рассмотрим задачу 179: [3, 49]
«Масса яблока 140 г, а масса груши на 60 г больше. Какова масса трех таких груш и яблок?»
|
Масса яблока -
|
Масса груши -
Какова масса трех таких груш и яблока?
Схематический рисунок этой задачи позволяет наглядно убедиться, что разница между массой яблока и массой груши составляет 60 г. При решении главное – понять, что сначала нужно найти массу одной груши. Поняв это, дети сами записывают решение.
Модели помогают найти разные способы решения одной и той же задачи.
«Движение является темой для самых разнообразных задач. Существует самостоятельный тип задач «на движение». Он объединяет такие задачи, которые решаются на основании зависимости между тремя величинами, характеризующими движение: скоростью, временем и расстоянием. Во всех случаях речь идет о равномерном прямолинейном движении» [28, 31].
«Основные объекты задач «на движение»: пройденный путь (s), скорость (v), время (t); основное отношение (зависимость): s = vt.» [9, 40]
Рассмотрим особенности решения основных видов задач «на движение».
Дата: 2019-07-24, просмотров: 191.
