Теплоемкостью тела называется величина, равная количеству теплоты dQ, которое нужно сообщить телу, чтобы повысить его температуру на единицу:

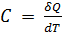                                                                                                   (1)

Стандартная единица теплоемкости – джоуль на кельвин (Дж/К).

Теплоемкость моля вещества называется молярной теплоемкостью С_m. Измеряется она в джоулях на моль-кельвин (Дж/(моль×К)).

Теплоемкость единицы массы вещества называется удельной теплоемкостью С_уд. Измеряется она в джоулях на килограмм-кельвин (Дж/(кг×К)). Удельная и молярная теплоемкости связаны соотношением:

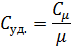
где m - молярная масса. При нагревании твердое тело не совершает работы над внешними телами, так как объем тела практически не меняется. Следовательно, согласно первому началу термодинамики (dq = dU + dА), все тепло идет на приращение внутренней энергии.

На основании (1) получаем:

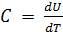                                             .                                                      (2)

В твердых телах частицы «закреплены» в определенных положениях равновесия, отвечающих минимуму энергии взаимодействия их друг с другом. Частицы могут совершать только колебания около равновесного положения в узлах кристаллической решетки. Направление колебаний непрерывно и хаотически меняется с течением времени.

В случае химически простых веществ это число равно числу Авогадро:

                                    U_m = N_A·3kT = 3RT,                                             (3)

где R = kN_A - универсальная газовая постоянная. Тогда, согласно (2), молярная теплоемкость твердого тела должна быть равна:

                                             C_m = 3R.                                                      (4)

Так как R = 8,314 Дж/(моль×K), то С_m » 25 Дж/(моль·К). Следовательно, теплоемкость моля химически простых тел в кристаллическом состоянии одинакова и равна 3R. Это утверждение называется законом Дюлонга – Пти.

Если твердое тело является химическим соединением, например, NaCl, то его кристаллическая решетка построена из атомов различных типов. Если в молекуле n атомов, и каждый атом обладает энергией 3k Т, то на молекулу придется в среднем энергия 3n кТ. Молярная теплоемкость будет равна C_m = 3nkN_A = 3nR, т. е. в n раз больше, чем у того же вещества при одноатомной молекуле. В кристалле каменной соли мы имеем расположенными по узлам решетки ионы Na⁺ и Cl^-, общее число которых в моле равно 2N_А.

Молярная теплоемкость кристаллической каменной соли должна равняться С_m = 6kN_A = 6R. В общем случае, молярная теплоемкость твердого соединения равна сумме молярных теплоемкостей элементов, из которых оно состоит, это правило было установлено эмпирически и называется законом Джоуля – Коппа.

Указанные законы выполняются с хорошим приближением для многих веществ при комнатной температуре. При понижении температуры теплоемкость твердого тела уменьшается, стремится к нулю при абсолютном нуле. У алмаза и бора теплоемкость при комнатной температуре оказалась ниже 3R.

Колеблющийся атом следует уподоблять не классическому, а квантовому осциллятору, обладающему дискретным энергетическим спектром. Энергия линейного осциллятора, согласно квантовой теории, есть целое кратное величины hn/e_n= nh, где h - постоянная Планка, n – любое целое число. Средняя энергия такого осциллятора вычисляется по формуле Планка:

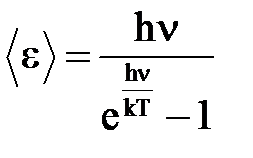                                          .                                                 (5)

При высоких температурах, так как hn<< kT, имеем:

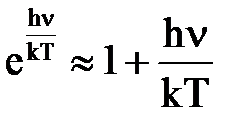
и формула (5) переходит в классическую: <e_n> = kT.

Основу теории Эйнштейна составляет представление о твердом теле как совокупности N независимых атомов - осцилляторов, колеблющихся с одинаковой частотой n. Средняя энергия, приходящаяся на одну степень свободы осциллятора <e>, определяется формулой (5).

Осцилляторы считаются трехмерными, т. е. имеющими три степени свободы. Поэтому средняя энергия тепловых колебаний одного атома равна 3<e>, а внутренняя энергия одного моля твердого тела определяется выражением:

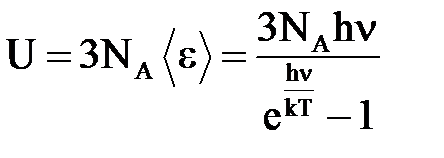                                  .                                          (6)

Отсюда

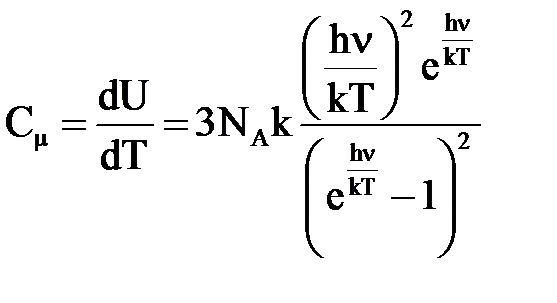                              .                                      (7)

При больших T (hv/kT << 1) имеем С_μ =3R, т. е. выражение (7) переходит в закон Дюлонга и Пти. В случае низких температур, когда hv/kT >> 1, можно пренебречь единицей в знаменателе (7):

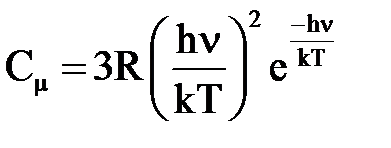                                    .                                             (8)

При Т ® 0 выражения (7) и (8) стремятся к нулю, в полном соответствии с опытом (h n/kT ® ¥; exp(–h n/kT) ® 0). Поскольку экспонента убывает значительно быстрее, то:

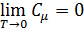
С точки зрения квантовой теории теплоемкости, тот факт, что некоторые вещества (алмаз, бор и другие) не подчиняются закону Дюлонга – Пти даже при комнатных температурах, объяснятся именно тем, что у этих веществ характеристическая температура Дебая настолько высока, что комнатная температура должна считаться низкой температурой (если для серебра q = 210 °С, для алюминия q = 400 °С, для свинца q = 90 °С, то для алмаза q = 2000 °С).

Удельная теплоемкость твердого тела определяется по формуле:

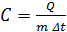                                             ,                                                      (9)

где С - удельная теплоемкость тела;

Q - количество теплоты, поглощенное образцом при нагревании на 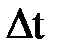; m – масса образца; Δt = t₂ – t₁ – разность конечной и начальной температур.

Если для нагрева пустого калориметра на Δt требуется количество теплоты Q₁, а для нагрева калориметра с исследуемым образцом на Δt – количество теплоты Q₂, то на нагрев самого образца идет количество теплоты:

                                        Q_обр = Q₂ - Q₁.                                               (10)

В установке ФПТ-8 нагрев производится пропусканием тока через нагреватель. Количество теплоты, выделяемое нагревателем, определяется по закону Джоуля – Ленца:

                                             Q = IUt                                                    (11)

I – ток, проходящий через нагреватель; U – напряжение на нагревателе; t – время нагрева.

Если мощность нагрева остается постоянной в течение всего эксперимента, то после подстановки выражения (11) в формулу (10) имеем:

                                      Q = IU × (t₂ - t₁),                                             (12)

t₁ – время нагрева пустого калориметра на Δt,

t₂ – время нагрева калориметра с образцом на Δt.

Тогда:

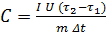                                         .                                                (13)