Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

к лабораторным работам по курсу

«Информационная безопасность»

(для студентов специальности 7.080403 “Программное обеспечение АС”)         

(Часть 1 – Криптографические и стеганографические методы защиты информации)

 

 

Донецк-ДонНТУ-2013

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

к лабораторным работам по курсу

«Информационная безопасность»

(для студентов специальности 7.080403 “Программное обеспечение АС”)

(Часть 1 – Криптографические и стеганографические методы защиты информации)

 

                                                   Рассмотрено на заседании кафедры

                                              КСМ

                                                                  Протокол № от

Утверждено на заседании

учебно-издательского Совета ДонНТУ

протокол № от  

 

Донецк –2013

УДК 681.3

        

    Методические указания и задания к лабораторным работам по курсу «Информационная безопасность» для студентов специальности «Программное обеспечение АС», часть 1 - «Криптографические и стеганографические методы защиты информации»/ Сост.: Губенко Н.Е., Чернышова А.В. - Донецк, ДонНТУ, 2013 - 89 стр.

 

 

    Приведены методические указания и задания к выполнению лабораторных работ по курсу «Информационная безопасность» для студентов специальности «Программное обеспечение АС». Излагаются вопросы, связанные с криптографическими и стеганографическими методами защиты информации. Рассматриваются простейшие базовые криптоалгоритмы, симметричные и ассиметричные криптосистемы, проверка подлинности информации средствами электронно-цифровой подписи, использование однонаправленных хэш-функций в криптографии, простейшие стеганографические алгоритмы защиты информации.

    Методические указания предназначены для усвоения теоретических основ и формирования практических навыков по курсу «информационная безопасность» по разделу «Криптографические и стеганографические методы защиты информации».

 

Составители:           доцент каф. КСМ, к.т.н. Губенко Н.Е.

                                 Ст.преп. каф. ПМиИ Чернышова А.В.

Рецензент:                   

Лабораторная работа №1

Тема: Базовые алгоритмы шифрования.

Цель: Изучить базовые алгоритмы шифрования и написать программу, выполняющую шифрование текста с помощью одного из базовых алгоритмов, выполнив предварительно модификацию базового алгоритма шифрования.

 Методические указания к лабораторной работе

Рассматриваемые простейшие методы кодирования заключаются в видоизменении информации таким образом, чтобы при попытке ее прочитать, злоумышленник не увидел ничего, кроме бессмысленной последовательности символов, а при попытке подделать или переделать документ, читатель, увидев ту же бессмыслицу, сразу понял бы это. Это и называется шифрованием или криптографией.

Зашифровав текст, его можно переправлять любым доступным способом, но никто не сможет узнать содержимое послания. Хотя, последнее не совсем верно, так как злоумышленник может попытаться раскрыть код.

Наука о раскрытии шифров – криптоанализ – всегда развивалась параллельно шифрованию. В последнее время, обе науки начали опираться на серьезный математический анализ, что только усилило их противоборство.

Не всегда криптоанализ используется злоумышленником. Дело в том, что преступная организация также может зашифровать послание. Тогда, дешифрация сообщения может оказаться жизненно важной. Поэтому, употреблять слово злоумышленник, говоря о шифровании, не совсем корректно, тем более, что в военном конфликте понятия прав и виноват весьма и весьма относительны. Но если сообщение шифруется, всегда есть опасность попытки его дешифрации.

Именно поэтому появился термин криптостойкость, то есть устойчивость алгоритма к криптоанализу.

    Прежде чем говорить о более сложных алгоритмах шифрования, рассмотрим базовые алгоритмы, которые частично используются в современных алгоритмах шифрования. К простейшим алгоритмам шифрования относятся:

- шифр Полибия;

- шифр Цезаря;

- шифр Ришелье;

- перестановочный шифр;

- шифр Виженера;

-    шифр Плейфера;

- шифрование с ключом;

- шифр Вернама;

- шифр «Люцифер»;

Многие криптосистемы, как простые, так и сложные основываются на принципах подставки, перестановки и гаммировании. Прежде чем рассматривать простейшие алгоритмы шифрования опишем в чем суть подстановок, перестановок и гаммирования, так как эти принципы являются базовыми.

Перестановки.

Перестановкой s набора целых чисел (0,1,...,N-1) называется его переупорядочение. Для того чтобы показать, что целое i пере­мещено из позиции i в позицию s(i), где 0 £ (i) < n, будем использовать запись

s=(s(0), s(1),..., s(N-1)).

Число перестановок из (0,1,...,N-1) равно n!=1*2*...*(N-1)*N. Введем обозначение s для взаимно-однозначного отображения (гомо­морфизма) набора S={s₀,s₁, ...,s_N-1}, состоящего из n элементов, на себя.

s: S ® S

s: s_i ® s_s(i), 0 £ i < n

Будем говорить, что в этом смысле s является перестановкой элементов S. И, наоборот, автоморфизм S соответствует пере­становке целых чисел (0,1,2,.., n-1).

Криптографическим преобразованием T для алфавита Z_m называется последовательность автоморфизмов: T={T⁽ⁿ⁾:1£n<¥}

T⁽ⁿ⁾: Z_m,n®Z_m,n, 1£n<¥

Каждое T⁽ⁿ⁾ является, таким образом, перестановкой n-грамм из Z_m,n.

Поскольку T⁽ⁱ⁾ и T^(j) могут быть определены независимо при i¹j, число криптографических преобразований исходного текста размерности n равно (mⁿ)! (Здесь и далее m - объем используемого алфавита.). Оно возрастает непропорционально при увеличении m и n: так, при m=33 и n=2 число различных криптографических преобразований равно 1089!. Отсюда следует, что потенциально существует большое число отображений исходного текста в шифрованный.

Практическая реализация криптогра­фических систем требует, чтобы преобразо­вания {T_k: kÎK} были определены алгоритмами, зависящими от относительно небольшого числа параметров (ключей).

Сис­те­мы под­ста­но­вок.

Определение Подстановкой p на алфавите Z_m называется автоморфизм Z_m, при котором буквы исходного текста t замещены буквами шифрованного текста p(t):

Z_m à Z_m; p: t à p(t).

Набор всех подстановок называется симметрической группой Z_m è будет в дальнейшем обозначаться как SYM(Z_m).

Утверждение SYM(Z_m) c операцией произведения является группой, т.е. операцией, обладающей следующими свойствами:

Замкнутость: произведение подстановок p₁p₂ является подста­новкой:

p: tàp₁(p₂(t)).

Ассоциативность: результат произведения p₁p₂p₃ не зависит от порядка расстановки скобок:

(p₁p₂)p₃=p₁(p₂p₃)

Существование нейтрального элемента: постановка i, опре­деляемая как i(t)=t, 0£t<m, является нейтральным элементом SYM(Z_m) по операции умножения: ip=pi для "pÎSYM(Z_m).

Существование обратного: для любой подстановки p существует единственная обратная подстановка p^-1, удовлетворя­ющая условию

pp^‑1=p^‑1p=i.

Число возможных подстановок в симметрической группе Z_m называется порядком SYM(Z_m) и равно m! .   

Определение. Ключом подстановки k для Z_m называется последовательность элементов симметрической группы Z_m:

k=(p₀,p₁,...,p_n-1,...), p_nÎSYM(Z_m), 0£n<¥

Подстановка, определяемая ключом k, является крипто­гра­фи­ческим преобразованием T_k, при помощи которого осуществляется преоб­разование n-граммы исходного текста (x₀ ,x₁ ,..,x_n-1) в n-грамму шифрованного текста (y₀ ,y₁ ,...,y_n-1):

y_i=p(x_i),   0£i<n

где n – произвольное (n=1,2,..). T_k называется моноалфавитной под­ста­новкой, если p неизменно при любом i, i=0,1,..., в противном случае T_k называется многоалфавитной подстановкой.

Примечание. К наиболее существенным особенностям подста­новки T_k относятся следующие:

1. Исходный текст шифруется посимвольно. Шифрования n-граммы (x₀ ,x₁ ,..,x_n-1) и ее префикса (x₀ ,x₁ ,..,x_s-1) связаны соотношениями

T_k(x₀ ,x₁ ,..,x_n-1)=(y₀ ,y₁ ,...,y_n-1)

T_k(x₀ ,x₁ ,..,x_s-1)=(y₀ ,y₁ ,...,y_s-1)

2. Буква шифрованного текста y_i является функцией только i-й компоненты ключа p_i и i-й буквы исходного текста x_i.

В потоковых шифрах, т. е. при шифровании потока данных, каждый бит исходной информации шифруется независимо от других с помощью гаммирования.

Гаммирование - наложение на открытые данные гаммы шифра (случайной или псевдослучайной последовательности единиц и нулей) по определенному правилу. Обычно используется "исключающее ИЛИ", называемое также сложением по модулю 2 и реализуемое в ассемблерных программах командой XOR. Для расшифровывания та же гамма накладывается на зашифрованные данные.

При однократном использовании случайной гаммы одинакового размера с зашифровываемыми данными взлом кода невозможен (так называемые криптосистемы с одноразовым или бесконечным ключом). В данном случае "бесконечный" означает, что гамма не повторяется.

В некоторых потоковых шифрах ключ короче сообщения. Так, в системе Вернама для телеграфа используется бумажное кольцо, содержащее гамму. Конечно, стойкость такого шифра не идеальна.

Понятно, что обмен ключами размером с шифруемую информацию не всегда уместен. Поэтому чаще используют гамму, получаемую с помощью генератора псевдослучайных чисел (ПСЧ). В этом случае ключ - порождающее число (начальное значение, вектор инициализации, initializing value, IV) для запуска генератора ПСЧ. Каждый генератор ПСЧ имеет период, после которого генерируемая последовательность повторяется. Очевидно, что период псевдослучайной гаммы должен превышать длину шифруемой информации.

Генератор ПСЧ считается корректным, если наблюдение фрагментов его выхода не позволяет восстановить пропущенные части или всю последовательность при известном алгоритме, но неизвестном начальном значении.

При использовании генератора ПСЧ возможно несколько вариантов:

1. Побитовое шифрование потока данных. Цифровой ключ используется в качестве начального значения генератора ПСЧ, а выходной поток битов суммируется по модулю 2 с исходной информацией. В таких системах отсутствует свойство распространения ошибок.

2. Побитовое шифрование потока данных с обратной связью (ОС) по шифртексту. Такая система аналогична предыдущей, за исключением того, что шифртекст возвращается в качестве параметра в генератор ПСЧ. Характерно свойство распространения ошибок. Область распространения ошибки зависит от структуры генератора ПСЧ.

3. Побитовое шифрование потока данных с ОС по исходному тексту. Базой генератора ПСЧ является исходная информация. Характерно свойство неограниченного распространения ошибки.

4. Побитовое шифрование потока данных с ОС по шифртексту и по исходному тексту.

Что­бы по­лу­чить ли­ней­ные по­сле­до­ва­тель­но­сти эле­мен­тов гам­мы, дли­на ко­то­рых пре­вы­ша­ет раз­мер шиф­руе­мых дан­ных, ис­поль­зу­ют­ся дат­чи­ки ПСЧ. На ос­но­ве тео­рии групп бы­ло раз­ра­бо­та­но не­сколь­ко ти­пов та­ких дат­чи­ков.

Конгруэнтные датчики

В на­стоя­щее вре­мя наи­бо­лее дос­туп­ны­ми и эф­фек­тив­ны­ми яв­ля­ют­ся кон­гру­энт­ные ге­не­ра­то­ры ПСП. Для это­го клас­са ге­не­ра­то­ров мож­но сде­лать ма­те­ма­ти­че­ски стро­гое за­клю­че­ние о том, ка­ки­ми свой­ст­ва­ми об­ла­да­ют вы­ход­ные сиг­на­лы этих ге­не­ра­то­ров с точ­ки зре­ния пе­рио­дич­но­сти и слу­чай­но­сти.

Од­ним из хо­ро­ших кон­гру­энт­ных ге­не­ра­то­ров яв­ля­ет­ся ли­ней­ный кон­гру­энт­ный дат­чик ПСЧ. Он вы­ра­ба­ты­ва­ет по­сле­до­ва­тель­но­сти псев­до­слу­чай­ных чи­сел T(i), опи­сы­вае­мые со­от­но­ше­ни­ем

T(i+1) = (A*T(i)+C) mod m,

где А и С - кон­стан­ты, Т(0) - ис­ход­ная ве­ли­чи­на, вы­бран­ная в ка­че­ст­ве по­ро­ж­даю­ще­го чис­ла. Оче­вид­но, что эти три ве­ли­чи­ны и об­ра­зу­ют ключ.

Та­кой дат­чик ПСЧ ге­не­ри­ру­ет псев­до­слу­чай­ные чис­ла с оп­ре­де­лен­ным пе­рио­дом по­вто­ре­ния, за­ви­ся­щим от вы­бран­ных зна­че­ний А и С. Зна­че­ние m обыч­но ус­та­нав­ли­ва­ет­ся рав­ным 2n , где n - дли­на машинного сло­ва в би­тах. Дат­чик име­ет мак­си­маль­ный пе­ри­од М до то­го, как ге­не­ри­руе­мая по­сле­до­ва­тель­ность нач­нет по­вто­рять­ся. По при­чи­не, от­ме­чен­ной ра­нее, не­об­хо­ди­мо вы­би­рать чис­ла А и С та­кие, что­бы пе­ри­од М был мак­си­маль­ным. Как по­ка­за­но Д. Кну­том, ли­ней­ный кон­гру­энт­ный дат­чик ПСЧ име­ет мак­си­маль­ную дли­ну М то­гда и толь­ко то­гда, ко­гда С - не­чет­ное, и А mod 4 = 1.

Для шиф­ро­ва­ния дан­ных с по­мо­щью дат­чи­ка ПСЧ мо­жет быть вы­бран ключ лю­бо­го раз­ме­ра. На­при­мер, пусть ключ со­сто­ит из на­бо­ра чи­сел x(j) раз­мер­но­стью b, где j=1, 2, ..., n. То­гда соз­да­вае­мую гам­му шиф­ра G мож­но пред­ста­вить как объ­е­ди­не­ние не­пе­ре­се­каю­щих­ся мно­жеств H(j).

Шиф­ро­ва­ние с по­мо­щью дат­чи­ка ПСЧ яв­ля­ет­ся до­воль­но рас­про­стра­нен­ным крип­то­гра­фи­че­ским ме­то­дом. Во мно­гом ка­че­ст­во шиф­ра, по­стро­ен­но­го на ос­но­ве дат­чи­ка ПСЧ, оп­ре­де­ля­ет­ся не толь­ко и не столь­ко ха­рак­те­ри­сти­ка­ми дат­чи­ка, сколь­ко ал­го­рит­мом по­лу­че­ния гам­мы. Один из фун­да­мен­таль­ных прин­ци­пов крип­то­ло­ги­че­ской прак­ти­ки гла­сит, да­же слож­ные шиф­ры мо­гут быть очень чув­ст­ви­тель­ны к про­стым воз­дей­ст­ви­ям.

 

Рассмотрим базовые алгоритмы подробнее.

Шифр Полибия.

Самый, пожалуй, древний из всех известных, хотя и не такой распространенный, как шифр Цезаря. Полибий, греческий историк, умер за тридцать лет до появления Цезаря. Суть его метода в том, что составляется прямоугольник (Доска Полибия), например такой, как представлен на рисунке 1.1.

	А	Б	В	Г	Д	Е
А	А	Б	В	Г	Д	Е
Б	Ж	З	И	Й	К	Л
В	М	Н	О	П	Р	С
Г	Т	У	Ф	Х	Ц	Ч
Д	Ш	Щ	Ъ	Ы	Ь	Э
Е	Ю	Я	.	,	-

Рисунок 1.1 – Доска Полибия

Каждая буква может быть представлена парой букв, указывающих строку и столбец, в которых расположена данная буква. Так, представлением букв П, О будут ВГ, ВВ соответственно, а сообщение ШИФР ПОЛИБИЯ зашифруется как ДАБВГВВДЕЕВГВВБЕБВАББВЕБ. Хоть эта система и является более древней, но устойчивость к раскрытию у нее гораздо выше, несмотря на то, что наблюдается увеличение количества символов зашифрованного текста.

Шифр Цезаря.

Первый документально подтвержденный шифр: Гай Юлий Цезарь, желая защитить свои записи, заменял каждую букву следующей по алфавиту. Можно расширить этот алгоритм, поставив в соответствие каждой букве, какую либо другую букву, разумеется, без повторений. Можно даже заменять буквы совершенно сторонними символами, это не повлияет на криптостойкость.

Во времена Цезаря, когда мало кто умел читать, да и статистика не была особенно развитой, такой шифр было почти невозможно взломать. Но теперь этот способ шифрования используют только в качестве головоломок.

Объяснить это легко. Посчитав вхождение каждого символа в тексте, и зная статистические особенности языка, то есть частоту появления каждого символа в текстах, можно смело заменить часть символов на настоящие. Остальной текст можно получить исходя из избыточности текстов на естественных языках. Очевидно также, что шифр Цезаря можно использовать только для текстов.

Это один из самых старых шифров, имеющий ряд серьезных недостатков. Огромное семейство подстановок Цезаря названо по имени римского императора Гая Юлия Цезаря, который поручал Марку Туллию Цицерону составлять послания с использованием 50-буквенного греческого алфавита со сдвигом в 3 знака и дальнейшей подстановкой. Информация об этом дошла к нам от Светония. Попробуем воспроизвести этот метод шифрования для русского алфавита. Для этого создадим таблицу соответствия (рис. 1.2):

Рисунок 1.2 – Пример таблицы соответствия букв русского алфавита

Шифр Ришелье.

Совершенно “естественно” выглядит криптотекст, полученный с помощью криптосистемы Ришелье. Соответственно, защищенность этого алгоритма гораздо выше предыдущих. В основе лежит “замешивание” по определенным законам исходного текста в “мусоре”, или посторонних символах. Зашифрованный текст получается гораздо длиннее исходного, причем эта разница и определяет реальную криптостойкость системы. Суть метода Ришелье в следующем. Создается подобная решетка с прорезями вместо крестов (рис. 1.3):

Х	Х						Х		Х
Х	Х				Х			Х
						Х
Х		Х	Х	Х					Х
							Х		Х
	Х			Х	Х		Х		Х

Рисунок 1.3 – Пример решетки Ришелье

Далее в прорезях отверстий пишется текст, решетка снимается и все оставшееся пространство заполняется “мусором”, затем для усложнения расшифровки криптотекст можно выписать в ряд. Для длинных сообщений этот метод применяется несколько раз. Кстати говоря, выходной криптотекст можно оформить с помощью “мусора” и в виде смыслового послания. Выполнить обратное преобразование в исходный текст можно, зная размер блока и имея аналогичную решетку.

 

Перестановочные шифры.

Этот шифр тоже является одним из первых, он предполагает разбиение текста на блоки, а затем перемешивание символов внутри блока. Это можно сделать разными методами. В первых вариантах этого шифра использовалась таблица, которую заполняли по строкам исходными данными, а зашифрованные данные читали по столбцам.

Криптостойкость этого шифра также оставляет желать лучшего. Дело в том, что филологи уже давно установили, что для прочтения текста не важен порядок букв в слове, достаточно чтобы на месте были первая и последняя буквы слова. Конечно, размер блока не может совпадать с размерами всех слов текста, то есть перемешивание будет более серьезным, но научится читать такой текст не очень сложно.

Рассмотрим этот метод на несложном алгоритме простой столбцевой перестановки. Предварительно условимся, что число столбцов равно пяти. Допустим, имеется текст, который требуется зашифровать: “ПРОСТЫЕ ПЕРЕСТАНОВКИ ВНОСЯТ СУМЯТИЦУ”. Запишем этот текст слева направо, сверху вниз, заполняя последовательно пять столбцов (рис 1.4):

1	2	3	4	5
П	Р	О	С	Т
Ы	Е		П	Е
Р	Е	С	Т	А
Н	О	В	К	И
	В	Н	О	С
Я	Т		С	У
М	Я	Т	И	Ц
У

Рисунок 1.4 – Пример простой столбцевой перестановки

Теперь зададимся ключом, например 35142, и выпишем в ряд столбцы, начиная с третьего, в соответствии с ключом: “О СВН Т ТЕАИСУЦ ПЫРН ЯМУСПТКОСИ РЕЕОВТЯ”. Получилось довольно неплохо. Для расшифровки требуется количество символов зашифрованного текста разделить на 5 и сформировать столбцы в соответствии с ключом.

В итоге получится исходная таблица, из которой можно прочитать текст построчно. Криптостойкость увеличится, если к полученному зашифрованному тексту применить повторное шифрование с другим размером таблицы и ключом или с перестановками не столбцов, а рядов. Перестановочные шифры очень хорошо сочетать с другими, таким образом повышая криптостойкость.

Шифр Виженера.

Наиболее известной и по праву одной из старейших многоалфавитных (одному шифруемому символу соответствует более одного символа) криптосистем является система известного французского криптографа графа Блейза Виженера (1523-1596).

Для преобразования строится алфавитный квадрат с построчным сдвигом символов в каждом последующем ряду (рисунок 1.5)

Рисунок 1.5 – Квадрат Виженера

Далее выбирается ключ. Затем пишется шифруемая фраза, а под ней циклически записывается ключ. Преобразование производится так: шифруемому символу соответствует символ, находящийся на пересечении буквы ключа (столбец) и буквы исходного текста (строка).

Одним и тем же буквам исходного текста соответствуют не всегда одинаковые символы, то есть символы могут принимать различные значения, что является несомненным плюсом в плане криптостойкости зашифрованного текста.

Далее выбирается ключ, например “ГРАФДРАКУЛА”. Затем пишется шифруемая фраза, а под ней циклически записывается ключ. Для примера возьмем фразу “ОТРЯД ЖДЕТ УКАЗАНИЙ” и исключим из нее пробелы:

“ОТРЯДЖДЕТУКАЗАНИЙ” – исходный текст, “ГРАФДРАКУЛАГРАФДР” – циклический ключ. Преобразование производится так: шифруемому символу соответствует символ, находящийся на пересечении буквы ключа (столбец) и буквы исходного текста (строка).

Получим: “СВРУИЦДПЕЮКГЧАБМЩ”. Как видно, одним и тем же буквам исходного текста соответствуют не всегда одинаковые символы, то есть символы могут принимать различные значения, что является несомненным плюсом в плане криптостойкости зашифрованного текста.

Квадрат может быть каким угодно, главное, чтобы он был легко воспроизводимым и левый столбец, так же как и верхний ряд, соответствовали всему алфавиту. В качестве альтернативного варианта это может быть известный квадрат Френсиса Бьюфорта, где строки – зеркальное отражение строк квадрата Виженера. Для усложнения строки могут быть переставлены местами в определенном порядке и т. д. Усложненной разновидностью этого метода является метод шифрования с автоключом, предложенный математиком Дж. Кардано (XVI в.). Суть его в том, что, кроме циклического ключа, есть еще один, записываемый однократно перед циклическим ключом – первичный ключ. Этот нехитрый прием придает дополнительную стойкость алгоритму.

Шифр Плейфейра.

Назван так в честь своего разработчика. Алгоритм заключается в следующем: сначала составляется равносторонний алфавитный квадрат. Для русского алфавита подойдет квадрат 5х6. Задается ключевая фраза без повторов букв, например “БАРОН ЛИС”. Фраза вписывается в квадрат без пробелов, далее последовательно вписываются недостающие буквы алфавита в правильной последовательности. Одну букву придется исключить для выполнения условия равносторонности. Пусть это будет Ъ. Примем допущение, что Ъ=Ь. Итак, получился квадрат, который легко восстановить по памяти:

Теперь условия для преобразования:

1) Текст должен иметь четное количество букв и делиться на биграммы (сочетания по две буквы), недостающую часть текста дополняем самостоятельно одним (любым) символом. Например, текст “ОСЕНЬ” преобразуется в “ОСЕНЬА”.

2) Биграмма не должна содержать одинаковых букв – “СОСНА” – “СО СН АБ”.

Б	А	Р	О	Н
Л	И	С	В	Г
Д	Е	Ж	З	К
М	П	Т	У	Ф
Х	Ц	Ч	Ш	Щ
Ь	Ы	Э	Ю	Я

Рисунок 1.6 – Пример алфавитного квадрата для шифрования методом Плейфера

Правила преобразования:

Если биграмма не попадает в одну строку или столбец, то мы смотрим на буквы в углах прямоугольника, образованного рассматриваемыми буквами. Например: “ДИ” = “ЛЕ”, “ЬУ” = “МЮ” и т. д.

Если биграмма попадает в одну строку (столбец), мы циклично смещаемся на одну букву вправо (вниз). Например, “ЛС”=“ИВ”, “ТЭ”=“ЧР”.

Итак, мы готовы преобразовать текст. Приступим к шифрованию:

“СОВЕЩАНИЕ СОСТОИТСЯ В ПЯТНИЦУ” – первоначально преобразуется в биграммы: “СО ВЕ ЩА НИ ЕС ОС ТО ИТ СЯ ВП ЯТ НИ ЦУ”. Выполнив преобразование по вышеизложенным правилам, получим биграммы: “РВ ЗИ НЦ ГА ИЖ ВР РУ ПС ЭГ УИ ФЭ ГА ПШ”.

Обратите внимание на то, что одинаковые буквы на входе дали разные буквы на выходе криптосистемы, а одинаковые буквы на выходе совсем не соответствуют одинаковым на входе. Таким образом, криптотекст “РВЗИНЦГАИЖВРРУПСЭГУИ” выглядит гораздо более “симпатично”, чем после прямой замены моноалфавитной криптосистемы.

Правила преобразования могут значительно варьироваться. Алфавит может быть упрощен до логического минимума с целью сокращения квадрата. Например, можно переводить текст в транслитерацию и писать латинскими буквами, тогда квадрат будет размером 5х5.

 

Шифрование с ключом.

Этот метод относится к современному периоду.

Текст представляется в двоичном формате, создается двоичный код некоторого размера (ключ), двоичный текст разбивается на блоки того же размера и каждый блок суммируется по модулю два с ключом. Обратное преобразование выполняется тем же методом.

Фактически, это «современный шифр Цезаря», просто подстановка выполняется не посимвольно, а словами. Правда, понятие слова здесь несколько иное – это блок заданной длины.

Криптостойкость этого метода намного выше, чем у предыдущих шифров. Без использования специальных методов криптоанализа его будет очень сложно взломать. Но в настоящее время этот метод используют только для не очень важных документов, так как криптоанализ, в совокупности с современными вычислительными средствами, позволяет не только прочесть текст сообщения, но и во многих случаях получить ключ, что губительно для системы безопасности.

 

Система Вернама.

В 1949 году, Шеннон сформулировал и доказал свою «пессимистическую теорему»: шифр является абсолютно криптостойким тогда и только тогда, когда энтропия ключа больше либо равна энтропии исходного текста. Из теоремы следует, что длина ключа должна быть соразмерна с длиной текста. Если быть более точным, длина ключа должна равняться длине текста.

На основе этой теоремы построена система Вернама. Каждый бит ключа этой системы равновероятно равен 0 либо 1. Длина ключа равна длине текста. Ключ используется только один раз. Доказано, что этот шифр абсолютно не вскрываем. Не будем этого доказывать, но обоснуем.

Для вскрытия шифрованного сообщения необходимо перебрать все возможные комбинации ключей (это единственный способ, так как ключ используется лишь единожды), и среди полученных значений текста выбрать исходный, пусть это будет текст на русском языке. Допустим, что злоумышленник может это сделать мгновенно, то есть опустим временную сложность такой задачи. Для текста любой длины, будет много бессмысленных результатов и их можно отбросить, но злоумышленник получит все возможные тексты заданной длины, в том числе наш текст. Но ничто и никогда не укажет на то, какой из текстов является исходным.

Рассмотрим это на примере четырех буквенных имен. Пусть зашифровано имя «Даша», а ключ «АБВГ». Если используется кодировка ASCII, то зашифрованный текст выглядит следующим образом: ♦!j#. Как говорилось ранее, единственный способ дешифровать текст, полный перебор всех возможных ключей. Но очевидно, что существует такой ключ, суммирование с которым зашифрованного текста даст в результате «Маша», или даже «Миша». Но действительно, невозможно ответить на вопрос, какое из имен является исходным.

Возможно, что аналитик знает часть текста, например, он знает что это договор на продажу недвижимости, но не знает цену. В результате перебора, если на это хватит времени, он получит все возможные цены «заданной длины». То есть если цена трехзначная, аналитиком будет получена девятьсот одна различная цена. Таким образом, взлом системы Вернама не приведет к получению новой информации и является абсолютно невскрываемым.

Недостаток этой системы – длина ключа. Сам Вернам предлагал пересылать ключ курьером. При этом если курьер не довез ключ, можно сгенерировать новый ключ и снова его отправить. Однако такой механизм чрезвычайно неудобен, поэтому эта система не используется в настоящее время.

Этот шифр при его идеальности лишен помехоустойчивости, потому как изменение одного бита, практически невозможно отследить.

 

Шифры, основанные на системе Вернама.

Если мы не можем использовать очень длинный ключ, следует использовать короткий, удлиняя его по некоторому правилу. Было предпринято много попыток создать шифр, как можно более приближенный к системе Вернама.

Первой попыткой было использование ключа в качестве параметров генератора псевдослучайных последовательностей. На деле все системы сводились именно к этому. Но в некоторых случаях ключ получали за счет его преобразований, например, с помощью нелинейной функции.

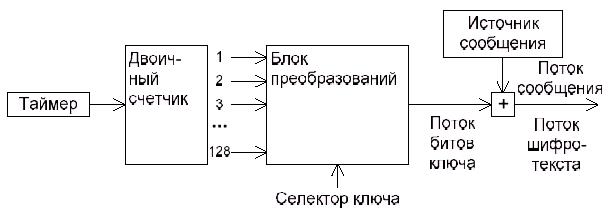
Рисунок 1.7 - Генерация ключа, для имитации системы Вернама

 

Наиболее удачной была схема, в которой ключ подавался на вход блоку преобразований (рисунок 1.7) одновременно с выходом двоичного счетчика, подключенного к таймеру. Для передачи сообщения правда требовалась большая синхронизация, нежели для системы Вернама, но вполне приемлемая.

 

Шифр «Люцифера».

Этот шифр изначально разрабатывался для аппаратной реализации. Именно при его создании одновременно использовались новейшие достижения в математике и теории кодирования и опыт веков.

«Люцифер» был создан фирмой IBM и долго использовался для внутренних нужд, так как аппаратная реализация системы шифрования имеет некоторые недостатки.

Авторы шифра предложили совместить два основных подхода к шифрованию: подстановки и перестановки.

Сначала, текст разбивается на блоки по n бит. Затем они поступают на вход мультиплексора, который раскладывает блок по модулю 2^n. Биты перемешиваются, и обрабатываются демультиплексором, который собирает биты в блок длиной n бит.

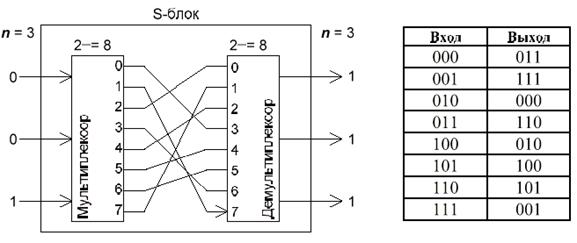
Рисунок 1.8 - Подстановки «Люцифера»

Преимущество таких постановок (Рисунок 1.8) заключается в нелинейности преобразований. По большому счету, можно любой входной поток превратить в любой выходной, но, разумеется, это производится на этапе разработки.

Выполнив подстановку, следует выполнить перестановки. Это делается соответствующей схемой, в которой просто перемешиваются биты (рисунок 1.9).

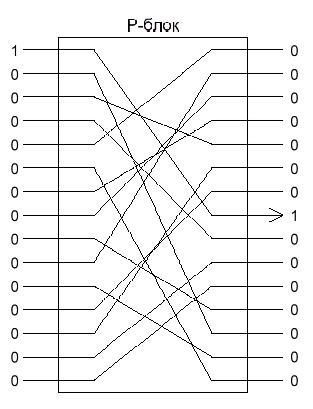
Рисунок 1.9 - Подстановки «Люцифера»

 

Узнать коммутацию такого блока довольно легко, достаточно подавать ровно одну единицу на вход, и получать ровно одну единицу на выходе. Однако, совместив оба подхода, и создавая как бы несколько итераций, можно очень сильно запутать аналитика (рисунок 1.10).

Легко увидеть, что если на вход подать одну единицу, на выходе получается больше единиц, чем нулей. Криптоаналитик, получивший текст, зашифрованный «Люцифером» будет поставлен в тупик.

 

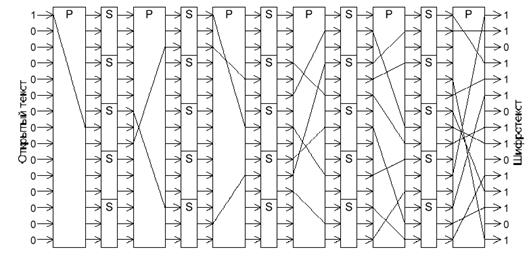
Рисунок 1.10 - «Люцифер»

 

Для этого шифра очень важно правильно подобрать параметры преобразований обоих типов. Дело в том, что при неудачном выборе параметров преобразований, они могут свестись к простой перестановке, которую легко раскрыть. Поэтому в аппаратную реализацию шифра встроили «сильные параметры.

Однако, аппаратная реализация шифра не позволяет его широкого применения, так как блок подстановок выполняет преобразование, схожее с суммированием с ключом, а суммирование с одним и тем же ключом ставит шифр под удар. С одной стороны, все, кто имеет доступ к системе, знают ключ, поэтому может произойти утечка, с другой стороны, аналитик, получивший достаточно много шифровок сможет таки дешифровать сообщение.

Было несколько попыток избавиться от этого недостатка, но наиболее удачная из них заключалась в том, чтобы каждый блок подстановок заменить двумя, при этом для шифрования, пользователь указывает первый или второй вид подстановок выполнять, создавая двоичный ключ (рисунок 1.11).

Такая реализация шифра была гораздо более криптостойкой и использовалась некоторое время.

 

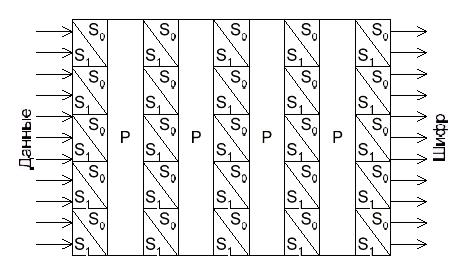
Рисунок 1.11 - «Люцифер» с ключом

 

Действительно криптостойкий шифр на основе «Люцифера» был предложен в 1973 году Хорстом Фейстелем. Этот алгоритм на самом деле является общим случаем «Люцифера».

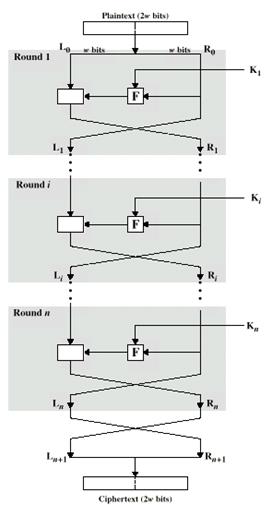
Рисунок 1.12 - Классическая сеть Фейстеля

Классическая (или простая) сеть Фейстеля (рисунок 1.12) разбивает исходный текст на блок длиной 2n бит, каждый блок разбивается на два потока L (левый) и R(правый). Далее выполняется преобразование по формуле:

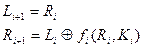
где Ki – ключ, Fi – функция преобразования.

Каждое такое действие называется раундом. Обычно используется 8-16 раундов. При этом, ключ в каждом раунде может быть как частью общего ключа, так и ее модификацией по некоторому правилу: следует отметить, что это в значительной мере влияет на криптостойкость. Также важным является правило, по которому текст разбивается на потоки.

Основное достоинство алгоритма заключается в том, что функция f не обязана быть обратимой, более того, для повышения криптостойкости обычно используют нелинейные именно необратимые функции.

Ключ, с которым суммируется текст не повторяется из блока в блок, а изменяется в зависимости от самого текста, это значительно увеличивает его энтропию, и, следовательно, увеличивает криптостойкость метода.

Процедура расшифровки очевидна, следует применить те же формулы, но в обратном порядке. Некоторые исследователи нашли способ применять один и тот же алгоритм и для шифровки, и для расшифровки, для этого необходимо удвоить число раундов, и во второй половине расположить функции и ключи в обратном порядке. Но как показали эксперименты, криптотойкость при таком подходе значительно ниже.

В последствии были построены сети Фейстеля с большим числом потоков. Это позволило также усложнить подход к функциям преобразования. На рисунке 1.13 представлены примеры таких сетей.

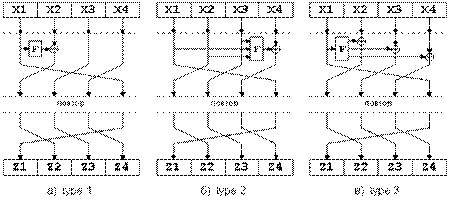
Рисунок 1.13 - Примеры сетей Фейстеля с большим числов потоков

Также существует несколько способов перемешивания: без него, симметричный, асимметричный, - представленные на рисунке 1.14.

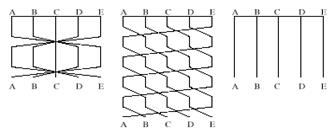
Рисунок 1.14 - Способы перемешивания потоков

Сравнивая сети Фейстеля с системой Вернама, становится очевидной высокая помехоустойчивость сетей Фейстеля: если система Вернама при искажении одного бита в зашифрованном тексте, искажала один бит в расшифрованном, то в сети Фейстеля этот бит повлияет на довольно большую часть текста и станет заметным, что позволит выявить случайные или преднамеренные искажения, и переслать шифрованный текст еще раз по другому каналу связи.

В последнее время появились упоминания так называемых Микро Декоррелированных Сетей Фейстеля. Суммируя текст с ключом, криптограф автоматически помещает информацию о ключе в зашифрованный текст, а получение ключа есть конечная цель любого криптоаналитика. Дэвид Вагнер, в своем труде «Атака бумерангом» описал способ уменьшить количество информации в тексте, зашифрованным сетью Фейстеля. Он предложил рассмотреть функции Fi как функции от текста, так, как если бы ключ был частью функции.    

Рассмотрим для примера функцию f(x)=ax+b по одной паре х и f(x) нельзя ничего сказать об а и b. Чем больше пар необходимо, тем лучше такая функция. Но в сетях Фейстеля, криптоаналитик в худшем случае знает исходный текст и зашифрованный тексты, то есть исходные данные и результат последней функции, что делает задачу криптоанализа в случае микро декоррелирующих сетей почти невыполнимой.

Существуют также динамические сети Фейстеля, причем существует несколько их вариантов.

Первый вариант, более простой, предполагает изменение величины блока от раунда к раунду. С одной стороны, это значительно увеличивает время шифрования, так как уже нельзя выбрав блок, сразу полностью произвести все преобразования. С другой стороны, это в значительной мере изменяет статистические характеристики текста. Это легко объяснить тем, что происходит более глубокое перемешивание битов текста. Подстановки в этом случае также несколько отличаются: так как на разных раундах производится подстановка слов различной длины, символы, попадающие в разные блоки, в зависимости от раунда, изменяются по-другому.

Второй вид динамических сетей фейстеля несколько сложнее. Он использует множества отображающих функций – определенное количество функций, по числу блоков, каждая из которых применяется в своем блоке. При этом множество функций изменяется от раунда к раунду. Это изменение также может быть простым перемешиванием, но в идеале, функции не должны повторяться вообще.

Рассматривают также и объединение двух видов динамических сетей Фейстеля. Когда каждый блок суммируется с результатом своей собственной функции, и количество блоков изменяется в зависимости от раунда.

 

 Задание к лабораторной работе

В соответствии с вариантом задания написать программу, реализующую один из базовых алгоритмов шифрования, при этом произвести некоторую модификацию выбранного алгоритма. Программа должна выполнять чтение файла, просмотр, его шифрование, расшифровывание, просмотр зашифрованного расшифрованного документа.

Отчет по лабораторной работе должен включать в себя: Краткое словесное описание базового алгоритма с его частичной модификацией, пример работы алгоритма, листинг программы, результаты работы программы.

Варианты заданий:

    № по журналу                           Базовый алгоритм

- 1-3                                              Шифр Полибия;

- 4-6                                              Шифр Цезаря;

- 7-9                                              Шифр Ришелье;

- 10-12                                                   Перестановочный шифр;

- 13-15                                                   Шифр Виженера

- 16-18                                                   Шифрование с ключем

- 19-21                                                   Шифр Вернама

21 – 25                                       Шифр Плейфейра.

-

Контрольные вопросы к лабораторной работе:

1) Что такое криптоанализ?

2) Что такое криптоскойкость алгоритма?

3) В чем суть перестановочных шифров?

4) В чем суть подстановочных шифров?

5) Назначение гаммирования.

6) Какой из рассмотренных базовых алгоритмов является по Вашему мнению наиболее криптостойким? Объяснить, почему.

7) Как, по Вашему мнению, можно увеличить криптостойкость алгоритма с использованием перестановок?

 

Лабораторная работа №2

Тема: Симметричные криптосистемы.

Цель работы: Изучение принципов шифрования в симметричных криптосистемах. Изучение классов преобразований в симметричных криптосистемах.

Методические указания к выполнению лабораторной работы

Криптографическая система это семейство преобразований шифра и совокупность ключей (т.е. алгоритм + ключи). Само по себе описание алгоритма не является криптосистемой. Только дополненное схемами распределения и управления ключами оно становится системой. Примеры алгоритмов – описания DES, ГОСТ28147-89. Дополненные алгоритмами выработки ключей, они превращаются в криптосистемы. Современные криптосистемы классифицируют следующим образом (рис. 2.1):

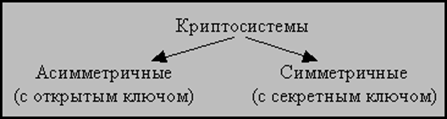
Рисунок 2.1 – Классификация криптосистем

Криптосистемы могут обеспечивать не только секретность передаваемых сообщений, но и их аутентичность (подлинность), а также подтверждение подлинности пользователя.

Симметричные криптосистемы (с секретным ключом - secret key systems) данные криптосистемы построены на основе сохранения в тайне ключа шифрования. Процессы зашифрования и расшифрования используют один и тот же ключ. Секретность ключа является постулатом. Основная проблема при применении симметричных криптосистем для связи заключается в сложности передачи обоим сторонам секретного ключа. Симметричные криптосистемы принято подразделять на блочные и поточные.

Блочные криптосистемы разбивают текст сообщения (файла, документа и т.д.) на отдельные блоки и затем осуществляют преобразование этих блоков с использованием ключа.

Поточные криптосистемы работают иначе. На основе ключа системы вырабатывается некая последовательность– так называемая выходная гамма, которая затем накладывается на текст сообщения. Таким образом, преобразование текста осуществляется как бы потоком по мере выработки гаммы.

 

Устройство блочных шифров.

Само преобразование шифра должно использовать следующие принципы (по К. Шеннону):

Рассеивание (diffusion) - т.е. изменение любого знака открытого текста или ключа влияет на большое число знаков шифротекста, что скрывает статистические свойства открытого текста;

Перемешивание (confusion) - использование преобразований, затрудняющих получение статистических зависимостей между шифротектстом и открытым текстом.

Практически все современные блочные шифры являются композиционными - т.е. состоят из композиции простых преобразований или F=F₁oF₂oF₃oF₄o..oF_n, где F - преобразование шифра, F_i - простое преобразование, называемое также i-ым циклом шифрования. Само по себе преобразование может и не обеспечивать нужных свойств, но их цепочка позволяет получить необходимый результат. Например, стандарт DES состоит из 16 циклов. Если же используется одно и то же преобразование, т.е. F_i постоянно для i, то такой композиционный шифр называют итерационным шифром.

Наибольшую популярность имеют шифры, устроенные по принципу шифра Фейстеля (Файстеля - Feistel), в которых:

1. Входной блок для каждого преобразования разбивается на две половины: p=(l,r), где l - левая, a r - правая;

2. Используется преобразование вида F_i (l,r)=(r,l Ä f_i(r)), где f_i– зависящая от ключа K_i функция, а Ä - операция XOR или некая другая.

Функция f_i называется цикловой функцией, а ключ K_i, используемый для получения функции f_i называется цикловым ключом. Как можно заметить, с цикловой функцией складывается только левая половина, а правая остается неизменной. Затем обе половины меняются местами. Это преобразование прокручивается несколько раз (несколько циклов) и выходом шифра является получившаяся в конце пара (l,r) Графически все выглядит следующим образом (рис. 2.2):

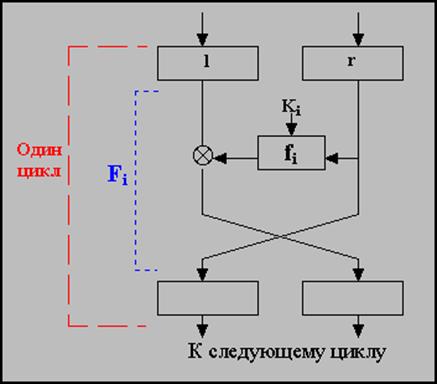
Рисунок 2.2 – Пример одного цикла преобразований

В качестве функции f_i выступает некая комбинация перестановок, подстановок, сдвигов, добавлений ключа и прочих преобразований. Так, при использовании подстановок информация проходит через специальные блоки, называемые S-блоками (S-боксами, S-boxes), в которых значение группы битов заменяется на другое значение. По такому принципу (с небольшими отличиями) построены многие алгоритмы: DES, ит.п. В других алгоритмах используются несколько иные принципы. Так, например, алгоритмы, построенные по SP-принципу (SP-сети) осуществляют преобразование, пропуская блок через последовательность подстановок (Substitutions) и перестановок (Permutations). Отсюда и название– SP-сети, т.е. сети "подстановок-перестановок". Примером такого алгоритма является очень перспективная разработка Rijndael. Саму идею построения криптографически стойкой системы путем последовательного применения относительно простых криптографических преобразований была высказана Шенноном (идея многократного шифрования).

Размеры блоков в каждом алгоритме свои. DES использует блоки по 64 бита (две половинки по 32 бита), LOKI97 - 128 бит.

Получение цикловых ключей.

Ключ имеет фиксированную длину. Однако при прокрутке хотя бы 8 циклов шифрования с размером блока, скажем, 128 бит даже при простом прибавлении посредством XOR потребуется 8*128=1024 бита ключа, поскольку нельзя добавлять в каждом цикле одно и то же значение ,так как это ослабляет шифр. Поэтому для получения последовательности ключевых бит придумывают специальный алгоритм выработки цикловых ключей (ключевое расписание - key schedule). В результате работы этого алгоритма из исходных бит ключа шифрования получается массив бит определенной длины, из которого по определенным правилам составляются цикловые ключи. Каждый шифр имеет свой алгоритм выработки цикловых ключей.

Режимы работы блочных шифров.

Чтобы использовать алгоритмы блочного шифрования для различных криптографических задач существует несколько режимов их работы. Наиболее часто встречающимися в практике являются следующие режимы:

­ электронная кодовая книга - ECB (Electronic Code Book);

­ сцепление блоков шифротекста - CBC (Cipher Block Chaining);

­ обратная связь по шифротектсту - CFB (Cipher Feed Back);

­ обратная связь по выходу - OFB (Output Feed Back).

Обозначим применение шифра к блоку открытого текста как E_k(M)=C, где k - ключ, M - блок открытого текста, а C - получающийся шифротекст.

Электронная Кодовая Книга (ECB)

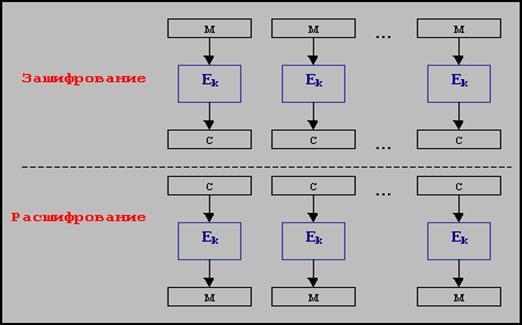
Рисунок 2.3 -  Схема электронной кодовой книги

 

Исходный текст разбивается на блоки, равные размеру блока шифра. Затем каждый блок шифруют независимо от других с использованием одного ключа шифрования (рис.2.3).

Непосредственно этот режим применяется для шифрования небольших объемов информации, размером не более одного блока или для шифрования ключей. Это связано с тем, что одинаковые блоки открытого текста преобразуются в одинаковые блоки шифротекста, что может дать взломщику (криптоаналитику) определенную информацию о содержании сообщения. К тому же, если он предполагает наличие определенных слов в сообщении (например, слово "Здравствуйте" в начале сообщения или "До свидания" в конце), то получается, что он обладает как фрагментом открытого текста, так и соответствующего шифротекста, что может сильно облегчить задачу нахождения ключа.

Основным достоинством этого режима является простота реализации.

Сцепление блоков шифротекста (CBC)

Один из наиболее часто применимых режимов шифрования для обработки больших количеств информации. Исходный текст разбивается на блоки, а затем обрабатывается по следующей схеме (рис.2):

1. Первый блок складывается побитно по модулю 2 (XOR) с неким значением IV – вектором инициализации (Init Vector), который выбирается независимо перед началом шифрования.

2. Полученное значение шифруется.

3. Полученный в результате блок шифротекста отправляется получателю и одновременно служит начальным вектором IV для следующего блока открытого текста.

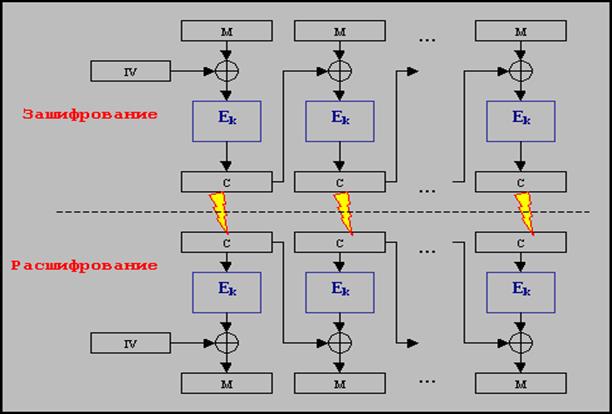
Рисунок 2.4 - Схема сцепления блоков шифротекста

 

Расшифрование осуществляется в обратном порядке.

В виде формулы, преобразование в режиме CBC можно представить как C_i=E_k(M_i Å C_i-1), где i - номер соответствующего блока. Из-за использования такого сцепления блоков шифротекста с открытым текстом пропадают указанные выше недостатки режима ECB, поскольку каждый последующий блок зависит от всех предыдущих. Если во время передачи один из блоков шифротекста исказится (передастся с ошибкой), то получатель сможет корректно расшифровать предыдущие блоки сообщения. Проблемы возникнут только с этим "бракованным" и следующим блоками. Одним из важных свойств этого режима является "распространение ошибки"– изменение блока открытого текста меняет все последующие блоки шифротекста. Поскольку последний блок шифротекста зависит от всех блоков открытого текста, то его можно использовать для контроля целостности и аутентичности (проверки подлинности) сообщения. Его называют кодом аутентификации сообщения (MAC - Message Authentication Code). Он может защитить как от случайных, так и преднамеренных изменений в сообщениях.

Обратная связь по шифротексту (CFB)

Режим может использоваться для получения поточного шифра из блочного. Размер блока в данном режиме меньше либо равен размеру блока шифра.

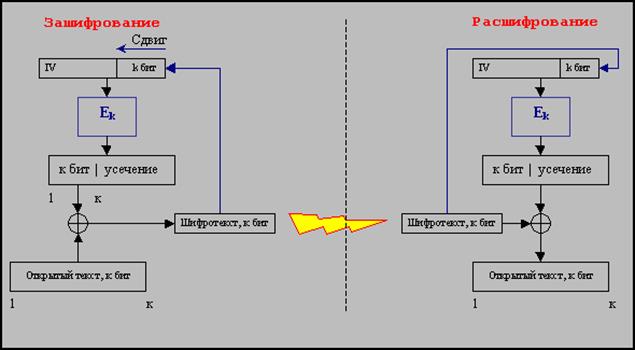
             Рисунок 2.5 -  Схема обратной связи по шифротексту

 

Описание работы схемы:

1. IV представляет собой сдвиговый регистр. Вначале IV заполняется неким значением, которое называется синхропосылкой, не является секретным и передается перед сеансом связи получателю.

2. Значение IV шифруется.

3. Берутся первые k бит зашифрованного значения IV и складываются (XOR) с k битами открытого текста. Получается блок шифротекста из k бит.

4. Значение IV сдвигается на k битов влево, а вместо него становится значение ш.т.

5. Затем опять 2 пункт и т.д до конца цикла шифрования.

Расшифрование происходит аналогично.

Особенностью данного режима является распространение ошибки на весь последующий текст. Рекомендованные значения k: 1 <= k <= 8.

Применяется, как правило, для шифрования потоков информации типа оцифрованной речи, видео.

Обратная связь по выходу (OFB)

Данный режим примечателен тем, что позволяет получать поточный шифр в его классическом виде, в отличии от режима CFB, в котором присутствует связь с шифротекстом. Принцип работы схож с принципом работы режима CFB, но сдвиговый регистр IV заполняется не битами шифротекста, а битами, выходящими из-под усечения.

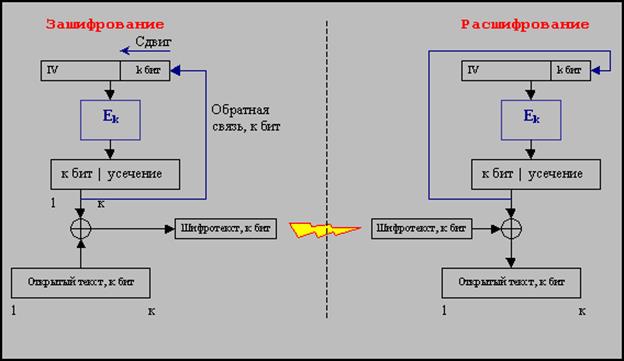
Рисунок 2.6 -  Схема обратной связи по выходу

Расшифрование осуществляется аналогично. То есть, для любого блока длины k операция зашифрования выглядит следующим образом: C_i=M_i Å G_i, где G_i - результат зашифрования некоторого вектора, являющегося заполнением сдвигового регистра. Главное свойство шифра – единичные ошибки не распространяются, т.к. заполнение сдвигового регистра осуществляется независимо от шифротекста.

Область применения: потоки видео, аудио или данных, для которых необходимо обеспечить оперативную доставку. Широко используется у военных наряду с поточными шифрами.

Описание MD 5

После некоторой первоначальной обработки MD5 обрабатывает входной текст 512-битовыми блоками, раз­битыми на 16 32-битовых подблоков. Выходом алгоритма является набор из четырех 32-битовых блоков, кото­рые объединяются в единое 128-битовое хэш-значение.

Во-первых, сообщение дополняется так, чтобы его длина была на 64 бита короче числа, кратного 512. Этим дополнением является 1, за которой вплоть до конца сообщения следует столько нулей, сколько нужно. Затем, к результату добавляется 64-битовое представление длины сообщения (истинной, до дополнения). Эти два дейст­вия служат для того, чтобы длина сообщения была кратна 512 битам (что требуется для оставшейся части алго­ритма), и чтобы гарантировать, что разные сообщения не будут выглядеть одинаково после дополнения. Инициализируются четыре переменных:

А = 0x01234567

В = 0x89abcdef

С = 0xfedcba98

D = 0x76543210

 

Они называются переменными сцепления.

Теперь перейдем к основному циклу алгоритма. Этот цикл продолжается, пока не исчерпаются 512-битовые блоки сообщения.

Четыре переменных копируются в другие переменные: А в а, В в b , С в с и D в d .

Главный цикл состоит из четырех очень похожих этапов. На каждом этапе 16 раз используются различные операции. Каждая операция представляет собой нелинейную функцию над тре­мя переменными из набора а, b , с и d . Затем она добавляет этот результат к четвертой переменной, подблоку текста и константе. Далее результат циклически сдвигается вправо на переменное число битов и добавляет результат к одной из переменных а, b , с и d . Наконец результат заменяет одну из переменных а, b , с и d . Существуют четыре нелинейных функции, используемые по одной в каждой операции (для каждого этапа - другая функция).

 

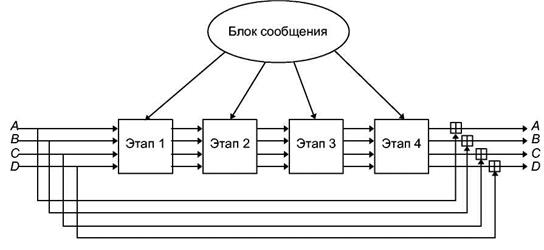
Рисунок 3.2 -  Главный цикл MD5

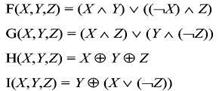
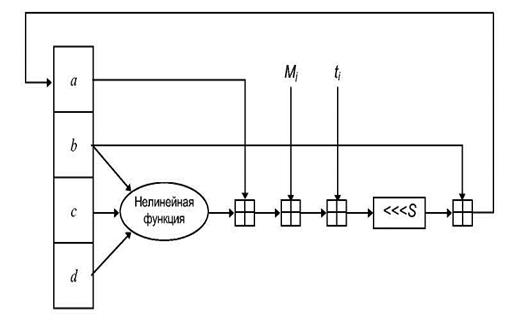
                  Рисунок 3.3 - Схема одной операции алгоритма MD5

Эти функции спроектированы так, чтобы, если соответствующие биты X , Y и Z независимы и несмещены, каждый бит результата также был бы независимым и несмещенным . Функция F - это побитовое условие: если X , то Y , иначе Z. Функция Н - побитовая операция четности.

Если Mj обозначает j-ый подблок сообщения (от 0 до 15), a <« s обозначает циклический сдвиг влево на s битов, то используются следующие четыре операции:

FF(a,b,c,d,Mj,s,t_i) означает a = b + ((a + ¥(b,c,d) + М,- + t_t) <«s)

GG(a,b,c,dMj,s,t_i) означает a = b + ((a + G(b,c,d) + Mj + t_t) <«s)

H H(a,b,c,d,Mj,s,t_i) означает a = b + ((a + H(b,c,d) + M,- + t_t) <«s)

II{a,b,c,dMj,s,t_i) означает a = b + ((a + I(b,c,d) + Mj + t_t) <«s)

Четыре этапа алгоритма.

Шаг 1: Добавление байтов заполнителей

Сообщение расширяется, так чтобы его длина (в битах) была 448 по модулю 512 – т.е. сообщению не хватает ровно 64 бит для кратности 512 битам. Добавление битов происходит в любом случае, даже если длина исходного сообщения изначально обладает этим свойством. Добавление происходит следующим образом:

- первый добавленный бит – «1», остальные «0». Минимум 1 бит, максимум 512.

Шаг 2: Добавление длины:

64 битное значение b (длины исходного сообщения) добавляется к сообщению. Если же длина более 2^64 (это маловероятно), то лишь младшие 64 бита длины используются.

Теперь сообщение имеет длину, кратную 512 битам (16 32 битных слова), его можно представить как слова:

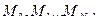, где N- кратно 16

Шаг 3: Инициализация буфера MD

Буфер из четырех слов (A,B,C,D), используется для расчета MD. Инициализируется:

word A: 01 23 45 67word B: 89 ab cd efword C: fe dc ba 98word D: 76 54 32 10

Шаг 4: Обработка сообщения блоками по 16 слов

Сначала определим четыре вспомогательных функции, на вход получают 3 слова, результат – слово.

F(X,Y,Z) = XY v not(X) Z

G(X,Y,Z) = XZ v Y not(Z)

H(X,Y,Z) = X xor Y xor Z

I(X,Y,Z) = Y xor (X v not(Z))

Каждый бит F – Если X то Y, иначе Z

Каждый бит G – Преобладающее значение X,Y,Z

Каждый бит H – xor, или контроль четности

Этот шаг использует специальную таблицу T[1..64], заполненную из значений синуса. T[i]=Целая часть 4294967296 * abs(sin(i)), где i в радианах.

       Делаем следующее:       Обрабатываем каждый блок в 16 слов. */ For i = 0 to N/16-1 do   /* Копируем блок i в X. */   For j = 0 to 15 do     X[j] = M[i*16+j].   end /* цикла j */   /* Сохраняем значения A как AA, B как BB, C как CC, и D как DD. */   AA = A   BB = B   CC = C   DD = D   /* Раунд 1. */

/* Пусть [abcd k s i] определяют операцию

     a = b + ((a + F(b,c,d) + X[k] + T[i]) <<< s). */

/* Делаем следующие 16 операций. */

[ABCD 0 7 1] [DABC 1 12 2] [CDAB 2 17 3] [BCDA 3 22 4]

[ABCD 4 7 5] [DABC 5 12 6] [CDAB 6 17 7] [BCDA 7 22 8]

[ABCD 8 7 9] [DABC 9 12 10] [CDAB 10 17 11] [BCDA 11 22 12]

[ABCD 12 7 13] [DABC 13 12 14] [CDAB 14 17 15] [BCDA 15 22 16]

 

    /* Раунд 2. */

/* Пусть [abcd k s i] определяют операцию

     a = b + ((a + G(b,c,d) + X[k] + T[i]) <<< s). */

/* Делаем следующие 16 операций. */

[ABCD 1 5 17] [DABC 6 9 18] [CDAB 11 14 19] [BCDA 0 20 20]

[ABCD 5 5 21] [DABC 10 9 22] [CDAB 15 14 23] [BCDA 4 20 24]

[ABCD 9 5 25] [DABC 14 9 26] [CDAB 3 14 27] [BCDA 8 20 28]

[ABCD 13 5 29] [DABC 2 9 30] [CDAB 7 14 31] [BCDA 12 20 32]

    /* Раунд 3. */

/* Пусть [abcd k s t] определяют операцию

     a = b + ((a + H(b,c,d) + X[k] + T[i]) <<< s). */

/* Делаем следующие 16 операций. */

[ABCD 5 4 33] [DABC 8 11 34] [CDAB 11 16 35] [BCDA 14 23 36]

[ABCD 1 4 37] [DABC 4 11 38] [CDAB 7 16 39] [BCDA 10 23 40]

[ABCD 13 4 41] [DABC 0 11 42] [CDAB 3 16 43] [BCDA 6 23 44]

[ABCD 9 4 45] [DABC 12 11 46] [CDAB 15 16 47] [BCDA 2 23 48]

 

/* Раунд 4. */

 /* Пусть [abcd k s t] определяют операцию

     a = b + ((a + I(b,c,d) + X[k] + T[i]) <<< s). */

/* Делаем следующие 16 операций. */

[ABCD 0 6 49] [DABC 7 10 50] [CDAB 14 15 51] [BCDA 5 21 52]

[ABCD 12 6 53] [DABC 3 10 54] [CDAB 10 15 55] [BCDA 1 21 56]

[ABCD 8 6 57] [DABC 15 10 58] [CDAB 6 15 59] [BCDA 13 21 60]

[ABCD 4 6 61] [DABC 11 10 62] [CDAB 2 15 63] [BCDA 9 21 64]

/* Изменяем ABCD – регистры для следующего блока */   A = A + AA   B = B + BB   C = C + CC   D = D + DD end /* цикла по i */

Шаг 5: Вывод

MD – это A,B,C,D – начиная с младшего байта A и заканчивая старшим байтом D (128 бит).

Безопасность MD 5

Рон Ривест привел следующие улучшения MD5 в сравнении с MD4 :

1. Добавился еще один этап.

2. Теперь в каждом действии используется уникальная прибавляемая константа .

3. Функция G на этапе 2 была изменена, чтобы сделать G менее симметричной.

4. Теперь каждое действие добавляется к результату предыдущего этапа. Это обеспечивает более быстрый лавинный эффект.

5. Изменился порядок, в котором использовались подблоки сообщения на этапах 2 и 3, чтобы сделать шаблоны менее похожими.

6. Значения циклического сдвига влево на каждом этапе были приближенно оптимизированы для ускорения лавинного эффекта. Четыре сдвига, используемые на каждом этапе, отличаются от значений, используемых на других этапах.

       MD 2

MD2 - это другая 128-битовая однонаправленная хэш-функция, разработанная Роном Ривестом. Она вместе с MD5 используется для цифровой подписи в протоколах РЕМ. Безопасность MD2 опирается на случайную перестановку байтов. Эта перестановка фиксирована и зависит от цифр числа pi. Идентификаторы So , S 1, S 2, , S 255  являются перестановкой.

Чтобы выполнить хэширование сообщения М необходимо:

1. Дополнить сообщение i байтами, значение i должно быть таким, чтобы длина полученного сообщения была кратна 16 байтам.

2. Добавить к сообщению 16 байтов контрольной суммы.

3. Проинициализировать 48-байтовый блок: Х_о, Х\, Х₂, . . ., Х_А1. Заполнить первые 16 байтов X нулями, во вторые 16 байтов X скопировать первые 16 байтов сообщения, а третьи 16 байтов X должны быть равны XOR первых и вторых 16 байтов X .

4. Вот как выглядит функция сжатия:
t  = 0

For j = 0 to 17

For к = 0 to 47

t = X_k XOR S_t,

X_k=t

t = (t +j) mod 256

5. Скопировать во вторые 16 байтов Xвторые 16 байтов сообщения, а третьи 16 байтов X должны быть равны XOR первых и вторых 16 байтов X . Выполнить этап (4). Повторять этапы (3) и (4) по очереди для каждых 16 байтов сообщения.

6. Выходом являются первые 16 байтов X .

Хотя в MD2 пока не было найдено слабых мест, она работает медленнее большинства других предлагаемых хэш-функций.

    Алгоритм безопасного хэширования ( Secure Hash Algorithm , SHA )

Алгоритм безопасного хэширования ( Secure Hash Algorithm, SHA), необходимый для обеспечения безопасности Алгоритма цифровой подписи (Digital Signature Algorithm, DSA). Для любого входного сообщения длиной меньше 2⁶⁴ битов SHA выдает 160-битовый результат, называемый кратким содержанием сообщения. Далее, краткое содержание сообщения становится входом DSA, который вычисляет подпись для сообщения.  Подписывание краткого содержания вместо всего сообщения часто повышает эффективность процесса, так как краткое содержание сообщения намного меньше, чем само сообщение. То же краткое содержание сообщения должно быть получено тем, кто проверяет подпись, если принятая им версия сообщения используется в качестве входа SHA. SHA называется безопасным, так как он разработан так, чтобы было вычислительно невозможно найти сообщение, соответствующее данному краткому содержанию сообщения или найти два различных сообщения с одинаковым кратким содержанием сообщения . Любые изменения, произошедшие при п ередаче сообщения, с очень высокой вероятностью приведут к изменению краткого содержания сообщения, и подпись не пройдет проверку.   Принципы, лежащие в основе SHA, аналогичны использованным профессором Рональдом Л. Ривестом  при проектировании алгоритма краткого содержания сообщения MD4. SHA разработан по образцу упомянутого алгоритма.

SHA выдает 160-битовое хэш-значение, более длинное, чем у MD5

Описание SHA

Во-первых, сообщение дополняется, чтобы его длина была кратной 512 битам. Используется то же дополне­ние, что и в MD5: сначала добавляется 1, а затем нули так, чтобы длина полученного сообщения была на 64 бита меньше числа, кратного 512, а затем добавляется 64-битовое представление длины оригинального сообщения.

Инициализируются пять 32-битовых переменных (в MD5 используется четыре переменных, но рассматри­ваемый алгоритм должен выдавать 160-битовое хэш-значение):

А = 0x67452301

В = 0xefcdab89

С = 0x10325476

D = 0x10325476

E = 0xc3d2elf0

Затем начинается главный цикл алгоритма. Он обрабатывает сообщение 512-битовыми блоками и продол­жается, пока не исчерпаются все блоки сообщения.

Сначала пять переменных копируются в другие переменные: А в а, В в b , С в с, D в d и Е в е.

Главный цикл состоит из четырех этапов по 20 операций в каждом (в MD5 четыре этапа по 16 операций в каждом). Каждая операция представляет собой нелинейную функцию над тремя из а, b , с, d и е, а затем выпол­няет сдвиг и сложение аналогично MD5. В SHA используется следующий набор нелинейных функций:

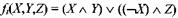 , для t=0 до 19  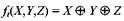, для t=20 до 39

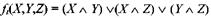 , для t=40 до 59  , для t=60 до 79 в алгоритме используются следующие четыре константы:

 К _t = 0х5а827999, для t=0 до 19

 К _t = 0x6ed9ebal , для t=20 до 39

К _t = 0x8flbbcdc, для t=40 до 59

 К _t = 0xca62cld6, для t=60 до 79

(Если интересно, как получены эти числа, то :0х5а827999 = 2^1/2/4, 0x6ed9ebal = 3^1/2/4, 0x8flbbcdc = 5^1/2/4, 0xca62cld6 = 10^1/2/4; все умножено на 2³²)

Блок сообщения превращается из 16 32-битовых слов (М_о по М₁₅) в 80 32-битовых слов ( W ₀ no W ₇₉ ) с помо­щью следующего алгоритма:

W_t = M_t , для t = 0 по 15

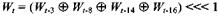 , для t=16 по 79

Если t - это номер операции (от 1 до 80), W , представляет собой t -ый подблок расширенного сообщения, а <<< - это циклический сдвиг влево на s битов, то главный цикл выглядит следующим образом:

FOR t = 0 to 79

TEMP = (а <<<5) +f_t(b,c,d) + e+W_t + K_t

e = d

d = c

c = b <<< 30

b = a

a = TEMP

Ha рисунке 3.4 показана одна операция. Сдвиг переменных выполняет ту же функцию, которую в MD5 выполняет использование в различных местах различных переменных.

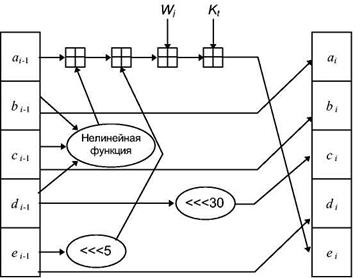
Рисунок 3.4 - Одна операция SHA.

После всего этого а, b , с, d и е добавляются к А, В, С D и Е, соответственно, и алгоритм продолжается для следующего блока данных. Окончательным результатом служит объединение А, В, С D и Е.

Безопасность SHA

    SHA очень похожа на MD4, но выдает 160-битовое хэш-значение. Главным изменением является введение расширяющего преобразования и добавление выхода предыдущего шага в следующий с целью получения более быстрого лавинного эффекта.

 

Задание к лабораторной работе

1. Изучить алгоритм и разработать программу реализации алгоритма хеш-функции в соответствии с вариантом:

- алгоритм MD 2  - <номер по журналу > MOD 4 =0;

- алгоритм MD 4 - <номер по журналу > MOD 4 =1;

- алгоритм MD 5 - <номер по журналу > MOD 4 =2;

- алгоритм SHA - <номер по журналу > MOD 4 =0;

2. Проанализировать алгоритм с точки зрения его безопасности.

Контрольные вопросы к лабораторной работе:

1. Какова кратность длины исходного сообщения?

2. Какова разрядность вычисленного хеш-значения?

3. Какие логические операции используются в алгоритме?

4. Для чего используется метод МД-усиления?

5. Для чего используются однонаправленные хеш-функции?

Лабораторная работа №4

Тема: Ассиметричные алгоритмы шифрования. Шифрование данных алгоритмом RSA. Понятия электронно-цифровой подписи. ЭЦП RSA.

Цель работы: Изучение принципов шифрования в ассиметричных криптосистемах. Изучение и программная реализация алгоритма RSA, ЭЦП RSA.

Методические указания к выполнению лабораторной работы

Про­цесс крип­то­гра­фи­че­ско­го за­кры­тия данных мо­жет осу­ще­ст­в­лять­ся как про­грамм­но, так и аппаратно. Ап­па­рат­ная реа­ли­за­ция от­ли­ча­ет­ся су­ще­ст­вен­но боль­шей стои­мо­стью, од­на­ко ей при­су­щи и пре­иму­ще­ст­ва: вы­со­кая про­из­во­ди­тель­ность, про­сто­та, за­щи­щен­ность и т.д. Про­грамм­ная реа­ли­за­ция бо­лее прак­тич­на, до­пус­ка­ет из­вест­ную гиб­кость в ис­поль­зо­ва­нии.

Для со­вре­мен­ных крип­то­гра­фи­че­ских сис­тем за­щи­ты ин­фор­ма­ции сфор­му­ли­ро­ва­ны сле­дую­щие об­ще­при­ня­тые тре­бо­ва­ния:

­ за­шиф­ро­ван­ное сообщение дол­жно под­да­вать­ся чте­нию толь­ко при на­ли­чии клю­ча;

­ чис­ло опе­ра­ций, не­об­хо­ди­мых для оп­ре­де­ле­ния ис­поль­зо­ван­но­го клю­ча шиф­ро­ва­ния по фраг­мен­ту шиф­ро­ван­но­го сообщения и со­от­вет­ст­вую­ще­го ему от­кры­то­го тек­ста, долж­но быть не мень­ше об­ще­го чис­ла воз­мож­ных клю­чей;

­ чис­ло опе­ра­ций, не­об­хо­ди­мых для рас­шиф­ро­вы­ва­ния ин­фор­ма­ции пу­тем пе­ре­бо­ра все­воз­мож­ных ключей долж­но иметь стро­гую ниж­нюю оцен­ку и вы­хо­дить за пре­де­лы воз­мож­но­стей со­вре­мен­ных ком­пь­ю­те­ров (с учетом возможности использования сетевых вычислений);

­ зна­ние ал­го­рит­ма шиф­ро­ва­ния не долж­но вли­ять на на­деж­ность за­щи­ты;

­ не­зна­чи­тель­ное из­ме­не­ние клю­ча долж­но при­во­дить к су­ще­ст­вен­но­му из­ме­не­нию ви­да за­шиф­ро­ван­но­го сообщения да­же при ис­поль­зо­ва­нии од­но­го и то­го же клю­ча;

­ струк­тур­ные эле­мен­ты ал­го­рит­ма шиф­ро­ва­ния долж­ны быть не­из­мен­ны­ми;

­ до­пол­ни­тель­ные би­ты, вво­ди­мые в сообщение в про­цес­се шиф­ро­ва­ния, должен быть пол­но­стью и на­деж­но скры­ты в шиф­ро­ван­ном тек­сте;

­ дли­на шиф­ро­ван­но­го тек­ста долж­на быть рав­ной дли­не ис­ход­но­го тек­ста;

­ не долж­но быть про­стых и лег­ко ус­та­нав­ли­вае­мых зависимостью ме­ж­ду клю­ча­ми, по­сле­до­ва­тель­но ис­поль­зуе­мы­ми в про­цес­се шиф­ро­ва­ния;

­ лю­бой ключ из мно­же­ст­ва возможных дол­жен обес­пе­чи­вать на­деж­ную за­щи­ту ин­фор­ма­ции;

­ ал­го­ритм должен до­пус­кать как про­грамм­ную, так и ап­па­рат­ную реа­ли­за­цию, при этом из­ме­не­ние длины к­лю­ча не долж­но вес­ти к ка­че­ст­вен­но­му ухуд­ше­нию ал­го­рит­ма шифрования.

Как бы ни бы­ли слож­ны и на­деж­ны симметричные крип­то­гра­фи­че­ские сис­те­мы - их сла­бое ме­сто при прак­ти­че­ской реа­ли­за­ции - про­блема рас­пре­де­ле­ния клю­чей. Для то­го, что­бы был воз­мо­жен об­мен кон­фи­ден­ци­аль­ной ин­фор­ма­ци­ей ме­ж­ду дву­мя субъ­ек­та­ми информационной системы, ключ дол­жен быть сге­не­ри­ро­ван од­ним из них, а за­тем ка­ким-то об­ра­зом опять же в кон­фи­ден­ци­аль­ном по­ряд­ке пе­ре­дан дру­го­му. Т.е. в об­щем слу­чае для пе­ре­да­чи клю­ча опять же тре­бу­ет­ся ис­поль­зо­ва­ние ка­кой-то крип­то­си­сте­мы.

Для ре­ше­ния этой про­бле­мы на ос­но­ве ре­зуль­та­тов, по­лу­чен­ных классической и со­вре­мен­ной ал­геб­рой, бы­ли пред­ло­же­ны сис­те­мы с от­кры­тым клю­чом.

Суть их со­сто­ит в том, что ка­ж­дым ад­ре­са­том ИС ге­не­ри­ру­ют­ся два клю­ча, свя­зан­ные ме­ж­ду со­бой по оп­ре­де­лен­но­му пра­ви­лу. Один ключ объ­яв­ля­ет­ся от­кры­тым, а дру­гой за­кры­тым. От­кры­тый ключ пуб­ли­ку­ет­ся и дос­ту­пен лю­бо­му, кто же­ла­ет по­слать со­об­ще­ние ад­ре­са­ту. Секретный ключ сохраняется в тайне.

Ис­ход­ный текст шиф­ру­ет­ся от­кры­тым клю­чом адресата и пе­ре­да­ет­ся ему. За­шиф­ро­ван­ный текст в прин­ци­пе не мо­жет быть рас­шиф­ро­ван тем же от­кры­тым клю­чом. Де­шиф­ро­ва­ние со­об­ще­ние воз­мож­но толь­ко с ис­поль­зо­ва­ни­ем за­кры­то­го клю­ча, ко­то­рый из­вес­тен толь­ко са­мо­му ад­ре­са­ту.

Крип­то­гра­фи­че­ские сис­те­мы с от­кры­тым клю­чом ис­поль­зу­ют так называемые  не­об­ра­ти­мые или од­но­сто­рон­ние функ­ции, ко­то­рые об­ла­да­ют сле­дую­щим свой­ст­вом: при за­дан­ном зна­че­нии x от­но­си­тель­но про­сто вы­чис­лить зна­че­ние f(x), од­на­ко ес­ли y=f(x), то нет про­сто­го пу­ти для вы­чис­ле­ния зна­че­ния x.

Мно­же­ст­во клас­сов не­об­ра­ти­мых функ­ций и по­ро­ж­да­ет все раз­но­об­ра­зие сис­тем с от­кры­тым клю­чом. Од­на­ко не вся­кая не­об­ра­ти­мая функ­ция го­дит­ся для ис­поль­зо­ва­ния в ре­аль­ных ИС.

В са­мом оп­ре­де­ле­нии не­об­ра­ти­мо­сти при­сут­ст­ву­ет не­оп­ре­де­лен­ность. Под необратимостью понимается не теоретическая необратимость, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства за обозримый интервал времени.

Обобщенная схема асимметричной криптосистемы с открытым ключом показана на рисунке 1. В этой криптосистеме применяют два различных ключа:

К_В – открытый ключ получателя В, используемый отправителем А:

k_В – секретный ключ получателя В.

Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ k_В по незащищенному каналу).

 

Рисунок 4.1 - Обобщенная схема асимметричной криптосистемы с открытым ключом

 

Процесс передачи зашифрованной информации в асимметричной криптосистеме осуществляется следующим образом:

1) Подготовительный этап:

- абонент В генерирует пару ключей: секретный ключ k_В и открытый ключ К_В ;

- открытый ключ К_В посылает абоненту А и остальным абонентам (или делается доступным, например, на разделяемом ресурсе).

2) Использование – обмен информацией между абонентами А и В:

- абонент А зашифровывает сообщение с помощью открытого ключа К_В абонента В и отправляет шифртекст абоненту В;

- абонент В расшифровывает сообщение с помощью своего секретного ключа k_В , Никто другой (в том числе абонент А) не может расшифровать данное сообщение, так как не имеет секретного ключа абонента В. Защита информации в асимметричной криптосистеме основана на секретности ключа k_В получателя сообщения.

Характерные особенности асимметричных криптосистем: открытый ключ и криптограмма могут быть отправлены по незащищенным каналам, то есть они известны противнику; алгоритмы шифрования и расшифрования являются открытыми.

По­это­му что­бы га­ран­ти­ро­вать на­деж­ную за­щи­ту ин­фор­ма­ции, к сис­те­мам с от­кры­тым клю­чом предъ­яв­ля­ют­ся два важ­ных и оче­вид­ных тре­бо­ва­ния:

1. Пре­об­ра­зо­ва­ние ис­ход­но­го тек­ста долж­но быть не­об­ра­ти­мым и ис­клю­чать его вос­ста­нов­ле­ние на ос­но­ве от­кры­то­го клю­ча.

2. Оп­ре­де­ле­ние за­кры­то­го клю­ча на ос­но­ве от­кры­то­го так­же долж­но быть не­воз­мож­ным на со­вре­мен­ном тех­но­ло­ги­че­ском уров­не. При этом же­ла­тель­на точ­ная ниж­няя оцен­ка сложности (ко­ли­че­ст­ва опе­ра­ций) рас­кры­тия шиф­ра.

Ал­го­рит­мы шиф­ро­ва­ния с от­кры­тым клю­чом по­лу­чи­ли ши­ро­кое рас­про­стра­не­ние в со­вре­мен­ных ин­фор­ма­ци­он­ных сис­те­мах. Так, ал­го­ритм RSA стал ми­ро­вым стан­дар­том де-фак­то для от­кры­тых сис­тем и ре­ко­мен­до­ван МККТТ.

Вообще же все предлагаемые сегодня криптосистемы с открытым ключом опираются на один из следующих типов необратимых преобразований:

1. Разложение больших чисел на простые множители.

2. Вычисление логарифма в конечном поле.

3. Вычисление корней алгебраических уравнений.

Здесь же сле­ду­ет от­ме­тить, что ал­го­рит­мы криптосистемы с открытым ключом  мож­но ис­поль­зо­вать в трех на­зна­че­ни­ях.

1. Как са­мо­стоя­тель­ные сред­ст­ва за­щи­ты пе­ре­да­вае­мых и хра­ни­мых дан­ных.

2. Как сред­ст­ва для рас­пре­де­ле­ния клю­чей. Ал­го­рит­мы рассматриваемой группы бо­лее тру­до­ем­ки, чем тра­ди­ци­он­ные крип­то­си­сте­мы. По­это­му час­то на прак­ти­ке ра­цио­наль­но с по­мо­щью систем с открытым ключом рас­пре­де­лять клю­чи, объ­ем ко­то­рых как ин­фор­ма­ции не­зна­чи­те­лен. А по­том с по­мо­щью обыч­ных ал­го­рит­мов осу­ще­ст­в­лять об­мен боль­ши­ми ин­фор­ма­ци­он­ны­ми по­то­ка­ми.

3. Сред­ст­ва ау­тен­ти­фи­ка­ции поль­зо­ва­те­лей (электронно-цифровая подпись).

Рассмотрим асимметричный алгоритм шифрования RSA.

Не­смот­ря на до­воль­но боль­шое чис­ло раз­лич­ных систем с открытым ключом, наиболее популярна - криптосистема RSA, разработанная в 1977 году и по­лу­чив­шая на­зва­ние в честь ее соз­да­те­лей: Рона Ри­ве­ста, Ади Ша­ми­ра и Леонарда Эй­дель­ма­на.

Они вос­поль­зо­ва­лись тем фак­том, что на­хо­ж­де­ние боль­ших про­стых чи­сел в вы­чис­ли­тель­ном от­но­ше­нии осу­ще­ст­в­ля­ет­ся лег­ко, но раз­ло­же­ние на мно­жи­те­ли про­из­ве­де­ния двух та­ких чи­сел прак­ти­че­ски не­вы­пол­ни­мо. До­ка­за­но (тео­ре­ма Ра­би­на), что рас­кры­тие шиф­ра RSA эк­ви­ва­лент­но та­ко­му раз­ло­же­нию. По­это­му для лю­бой дли­ны клю­ча мож­но дать ниж­нюю оцен­ку чис­ла опе­ра­ций для рас­кры­тия шиф­ра, а с уче­том про­из­во­ди­тель­но­сти со­вре­мен­ных ком­пь­ю­те­ров оце­нить и не­об­хо­ди­мое на это вре­мя.

Общее описание алгоритма RSA:

1. Отправитель выбирает два очень больших простых числа Р и Q и вычисляет два произведения N=PQ и M=(P-1)(Q-1).

2. Затем он выбирает случайное целое число D, взаимно простое с М, и вычисляет Е, удовлетворяющее условию DE = 1 MOD М.

3. После этого он публикует D и N как свой открытый ключ шифрования, сохраняя Е как закрытый ключ.

4. Если S - сообщение, длина которого, определяемая по значению выражаемого им целого числа, должна быть в интервале (1, N), то оно превращается в шифровку возведением в степень D по модулю N и отправляется получателю S'=(S**D) MOD N.

5. Получатель сообщения расшифровывает его, возводя в степень Е по модулю N, так как S =(S'**E) MOD N = (S**(D*E)) MOD N.

Таким образом, открытым ключом служит пара чисел N и D, а секретным ключом число Е. 

Воз­мож­ность га­ран­ти­ро­ван­но оце­нить за­щи­щен­ность ал­го­рит­ма RSA ста­ла од­ной из при­чин по­пу­ляр­но­сти этой системы с открытым ключом на фо­не де­сят­ков дру­гих схем. По­это­му ал­го­ритм RSA ис­поль­зу­ет­ся в бан­ков­ских ком­пь­ю­тер­ных се­тях, осо­бен­но для ра­бо­ты с уда­лен­ны­ми кли­ен­та­ми (об­слу­жи­ва­ние кре­дит­ных кар­то­чек).

В настоящее время алгоритм RSA используется во многих стандартах, среди которых SSL, S-HHTP, S-MIME, SWAN, STT и PCT.

Рас­смот­рим ма­те­ма­ти­че­ские ре­зуль­та­ты, по­ло­жен­ные в ос­но­ву это­го ал­го­рит­ма.

Теорема 1. (Малая теорема Ферма.)

Если р - простое число, то

x^p-1 = 1 (mod p)                            (1)

для любого х, простого относительно р, и

x^p = х (mod p)                             (2)

для любого х.

Доказательство. Достаточно доказать справедливость уравнений (1) и (2) для хÎZ^p. Проведем доказательство методом индукции.

Далее

x^p=(x-1+1)^p= å C(p,j)(x-1)^j=(x-1)^p+1 (mod p),

                                       0£j£p

так как C(p,j)=0(mod p) при 0<j<p. С учетом этого неравенства и предложений метода доказательства по индукции теорема доказана.

Определение. Функцией Эйлера j(n) называется число положительных целых, меньших n и простых относительно n.

n	2	3	4	5	6	7	8	9	10	11	12
j(n)	1	2	2	3	2	6	4	6	4	10	4

Теорема 2. Если n=pq, (p и q - отличные друг от друга простые числа), то

j(n)=(p-1)(q-1).

Теорема 3. Если n=pq, (p и q - отличные друг от друга простые числа) и х - простое относительно р и q, то

x^j(n) = 1 (mod n).

Следствие . Если n=pq, (p и q - отличные друг от друга простые числа) и е простое относительно j(n), то отображение

Е_e,n: x®x^e (mod n)

является взаимно однозначным на Z_n.

Очевиден и тот факт, что если е - простое относительно j(n), то существует целое d, такое, что

ed = 1 (mod j(n))                         (3)

На этих математических фактах и основан популярный алгоритм RSA.

Пусть n=pq, где p и q - различные простые числа. Если e и d удовлетворяют уравнению (8.2.3), то отображения Е_e,n и Е_d,n являются инверсиями на Z_n. Как Е_e,n, так и Е_d,n легко рассчитываются, когда известны e, d, p, q. Если известны e и n, но p и q неизвестны, то Е_e,n представляет собой одностороннюю функцию; нахождение Е_d,n по заданному n равносильно разложению n. Если p и q - достаточно большие простые, то разложение n практически не осуществимо. Это и заложено в основу системы шифрования RSA.

Пользователь i выбирает пару различных простых p_i и q_i и рассчитывает пару целых (e_i, d_i), которые являются простыми относительно j(n_i), где n_i=p_i q_i . Справочная таблица содержит публичные ключи {(e_i ,n_i)}.

Предположим, что исходный текст

x =(x₀, x₁, ..., x_n-1), xÎZ_n , 0 £ i < n,

сначала представлен по основанию n_i :

N = c₀+c_{i ni}+....

Пользователь i зашифровывает текст при передаче его пользователю j, применяя к n отображение Ed_i,n_i :

N ® Ed_i,n_i n = n’.

Пользователь j производит дешифрование n’, применяя Ee_i,n_i :

N’ ® Ee_i,n_i n’= Ee_i,n_i Ed_i,n_i n = n .

Очевидно, для того чтобы найти инверсию Ed_i,n_i по отношению к Ee_i,n_i, требуется знание множителей n=p_i q_i. Время выполнения наилучших из известных алгоритмов разложения при n=10¹⁰⁰ на сегодняшний день выходит за пределы современных технологических возможностей.

Рассмотрим небольшой пример, иллюстрирующий применение алгоритма RSA.

Пример: Зашифруем сообщение “САВ”. Для простоты будем использовать маленькие числа (на практике применяются гораздо большие).

1. Выберем p=3 и q=11.

2. Определим n=3*11=33.

3. Найдем (p-1)(q-1)=20. Следовательно, в качестве d, взаимно простое с 20, например, d=3.

4. Выберем число е. В качестве такого числа может быть взято любое число, для которого удовлетворяется соотношение (е*3) (mod 20) = 1, например 7.

5. Представим шифруемое сообщение как последовательность целых чисел с помощью отображения: А®1, В®2, С®3. Тогда сообщение принимает вид (3,1,2). Зашифруем сообщение с помощью ключа {7,33}.

ШТ1 = (3⁷) (mod 33) = 2187 (mod 33) = 9,

ШТ2 = (1⁷) (mod 33) = 1 (mod 33) = 1,

ШТ3 = (2⁷) (mod 33) = 128 (mod 33) = 29.

6. Расшифруем полученное зашифрованное сообщение (9,1,29) на основе закрытого ключа {3,33}:

ИТ1 = (9³) (mod 33) = 729 (mod 33) = 3,

ИТ2= (1³) (mod 33) = 1 (mod 33) = 1,

ИТ3 = (29³) (mod 33) = 24389 (mod 33) = 2.

Практическая реализация RSA

В настоящее время алгоритм RSA активно реализуется как в виде самостоятельных криптографических продуктов, так и в качестве встроенных средств в популярных приложениях.

Важная проблема практической реализации - генерация больших простых чисел. Решение задачи «в лоб» - генерация случайного большого числа n (нечетного) и проверка его делимости на множители от 3 вплоть до n ^0.5. В случае неуспеха следует взять n+2 и так далее.

В принципе в качестве p и q можно использовать «почти» простые числа, то есть числа для которых вероятность того, что они простые, стремится к 1. Но в случае, если использовано составное число, а не простое, криптостойкость RSA падает. Имеются неплохие алгоритмы, которые позволяют генерировать «почти» простые числа с уровнем доверия 2^-100.

Другая проблема - ключи какой длины следует использовать?

Для прак­ти­че­ской реа­ли­за­ции ал­го­рит­мов RSA по­лез­но знать оцен­ки тру­до­ем­ко­сти раз­ло­же­ния про­стых чи­сел раз­лич­ной дли­ны, сде­лан­ные Шроппелем.

log10 n	Число операций	Примечания
50	1.4*1010	Раскрываем на суперкомпьютерах
100	2.3*1015	На пределе современных технологий
200	1.2*1023	За пре­де­ла­ми со­вре­мен­ных тех­но­ло­гий
400	2.7*1034	Тре­бу­ет су­ще­ст­вен­ных из­ме­не­ний в тех­но­ло­гии
800	1.3*1051	Не раскрываем

 

Сами авторы RSA рекомендуют использовать следующие размеры модуля n:

­ 768 бит - для частных лиц;

­ 1024 бит - для коммерческой информации;

­ 2048 бит - для особо секретной информации.

Третий немаловажный аспект реализации RSA - вычислительный. Ведь приходится использовать аппарат длинной арифметики. Если используется ключ длиной k бит, то для операций по открытому ключу требуется О( k ² ) операций, по закрытому ключу - О( k ³ ) операций, а для генерации новых ключей требуется О( k ⁴ ) операций.

Криптографический пакет BSAFE 3.0 (RSA D.S.) на компьютере Pentium-90 осуществляет шифрование со скоростью 21.6 Кбит/c для 512-битного ключа и со скоростью 7.4 Кбит/c для 1024 битного. Самая «быстрая» аппаратная реализация обеспечивает скорости в 60 раз больше.

 

Где H - хеш сообщения,

S - его сигнатура,

D - секретный ключ,

E - открытый ключ.

Проверке подлинности посвящены стандарты:

    - проверка подлинности (аутентификация, authentication) - ISO 8730-90, ISO/IES 9594-90 и ITU X.509;

- целостность - ГОСТ 28147-89, ISO 8731-90;

- цифровая подпись - ISO 7498, P 34.10-94 (Россия), DSS (Digital Signature Standard, США).

Цифровая сигнатура

Часто возникают ситуации, когда получатель должен уметь доказать подлинность сообщения внешнему лицу. Чтобы иметь такую возможность, к передаваемым сообщениям должны быть приписаны так называемые цифровые сигнатуры.

Цифровая сигнатура - это строка символов, зависящая как от идентификатора отправителя, так и содержания сообщения.

 

 

 

Рисунок 4.1 - Цифровая сигнатура

Ни­кто при этом кро­ме поль­зо­ва­те­ля А не мо­жет вы­чис­лить циф­ро­вую сиг­на­ту­ру А для кон­крет­но­го со­об­ще­ния. Ни­кто, да­же сам поль­зо­ва­тель не мо­жет из­ме­нить по­слан­но­го со­об­ще­ния так, что­бы сиг­на­ту­ра ос­та­лась не­из­мен­ной. Хо­тя по­лу­ча­тель дол­жен иметь воз­мож­ность про­ве­рить яв­ля­ет­ся ли циф­ро­вая сиг­на­ту­ра со­об­ще­ния под­лин­ной. Что­бы про­ве­рить циф­ро­вую сиг­на­ту­ру, поль­зо­ва­тель В дол­жен пред­ста­вить по­сред­ни­ку С ин­фор­ма­цию, ко­то­рую он сам ис­поль­зо­вал для ве­ри­фи­ка­ции сиг­на­ту­ры.

Ес­ли по­ме­чен­ное сиг­на­ту­рой со­об­ще­ние пе­ре­да­ет­ся не­по­сред­ст­вен­но от от­пра­ви­те­ля к по­лу­ча­те­лю, ми­нуя про­ме­жу­точ­ное зве­но, то в этом слу­чае идет речь об ис­тин­ной циф­ро­вой сиг­на­ту­ре.

Рас­смот­рим ти­пич­ную схе­му циф­ро­вой сиг­на­ту­ры.

Пусть Е - функция симметричного шифрования и f - функция отображения некоторого множества сообщений на подмножество мощности р из последовательности {1, ..., n}.

Например р=3 и n=9. Если m - сообщение, то в качестве f можно взять функцию f(m) = {2, 5, 7}.

Для каждого сообщения пользователь А выбирает некоторое множество ключей K=[K₁, ..., K_n} и параметров V={v₁, ...,v_n} для использования в качестве пометок сообщения, которое будет послано В. Множества V и V’={E(v₁,K₁) ..., E(v_n,K_n)} посылаются пользователю В и заранее выбранному посреднику С.

Пусть m - сообщение и idm - объединение идентификационных номеров отправителя, получателя и номера сообщения. Если f({idm, m}), то цифровая сигнатура m есть множество K’=[K_i, ..., K_j}. Сообщение m, идентификационный номер idm и цифровая сигнатура К’ посылаются В.

 

 

Рисунок 4.2 – Использование посредника

Получатель В проверяет сигнатуру следующим образом. Он вычисляет функцию f({idm, m}) и проверяет ее равенство К’. Затем он проверяет, что подмножество {v_i, ...,v_j} правильно зашифровано в виде подмножества {E(v_i,K_i) ..., E(v_j,K_j)} множества V’.

В кон­фликт­ной си­туа­ции В по­сы­ла­ет С сообщение m, иден­ти­фи­ка­ци­он­ный но­мер idm и мно­же­ст­во клю­чей K’, ко­то­рое В объ­яв­ля­ет сиг­на­ту­рой m. То­гда по­сред­ник С так же, как и В, бу­дет спо­со­бен про­ве­рить сиг­на­ту­ру. Ве­ро­ят­ность рас­кры­тия двух со­об­ще­ний с од­ним и тем же зна­че­ни­ем функ­ции f долж­на быть очень ма­ла. Что­бы га­ран­ти­ро­вать это, чис­ло  n долж­но быть дос­та­точ­но боль­шим, а чис­ло р долж­но быть боль­ше 1, но мень­ше n.

Ряд не­дос­тат­ков этой мо­де­ли оче­ви­ден:

­  долж­но быть третье ли­цо - по­сред­ник, ко­то­ро­му до­ве­ря­ют как по­лу­ча­тель, так и от­пра­ви­тель;

­  по­лу­ча­тель, от­пра­ви­тель и по­сред­ник долж­ны об­ме­нять­ся су­ще­ст­вен­ным объ­е­мом ин­фор­ма­ции, пре­ж­де чем бу­дет пе­ре­да­но ре­аль­ное со­об­ще­ние;

­  пе­ре­да­ча этой ин­фор­ма­ции долж­на осу­ще­ст­в­лять­ся в за­кры­том ви­де;

­  эта ин­фор­ма­ция ис­поль­зу­ет­ся край­не не­эф­фек­тив­но, по­сколь­ку мно­же­ст­ва K, V, V’ ис­поль­зу­ют­ся толь­ко один раз.

Тем не ме­нее, да­же та­кая схе­ма циф­ро­вой сиг­на­ту­ры мо­жет ис­поль­зо­вать­ся в ин­фор­ма­ци­он­ных сис­те­мах, в ко­то­рых не­об­хо­ди­мо обес­пе­чить ау­тен­ти­фи­ка­цию и за­щи­ту пе­ре­да­вае­мых со­об­ще­ний.

Использование цифровой сигнатуры предполагает использование некоторых функций шифрования:

S = H( k, T),

где S - сигнатура, k - ключ, T - исходный текст.

Функция H( k, T) - является хэш-функцией, если она удовлетворяет следующим условиям:

1) исходный текст может быть произвольной длины;

2) само значение H( k, T) имеет фиксированную длину;

3) значение функции H( k, T) легко вычисляется для любого аргумента;

4) восстановить аргумент по значению с вычислительной точки зрения - практически невозможно;

функция H( k, T) – однозначна

При этом разделяют слабую и сильную однозначность. При слабой однозначности для заданного значения T практически невозможно отыскать другой текст Т’, для которого H( k, T) = H( k, T’). При сильной однозначности для любого текста T невозможно найти другой подходящий текст, имеющий то же значение хэш-функции

Из определения следует, что для любой хэш-функции есть тексты-близнецы - имеющие одинаковое значение хэш-функции, так как мощность множества аргументов неограниченно больше мощности множества значений. Такой факт получил название «эффект дня рождения». (Факт теории вероятностей: в группе из 23 человек с вероятностью больше 0.5 два и более человека родились в одно и то же число)

Наиболее известные из хэш-функций - MD2, MD4, MD5 и SHA.

Три алгоритма серии MD разработаны Ривестом в 1989-м, 90-м и 91-м году соответственно. Все они преобразуют текст произвольной длины в 128-битную сигнатуру.

Алгоритм MD2 предполагает:

­ дополнение текста до длины, кратной 128 битам;

­ вычисление 16-битной контрольной суммы (старшие разряды отбрасываются);

­ добавление контрольной суммы к тексту;

­ повторное вычисление контрольной суммы.

Алгоритм MD4 предусматривает:

­ дополнение текста до длины, равной 448 бит по модулю 512;

­ добавляется длина текста в 64-битном представлении;

­ 512-битные блоки подвергаются процедуре Damgard-Merkle, причем каждый блок участвует в трех разных циклах. (В отличие от хэш-функции - этот класс преобразований предполагает вычисление для аргументов фиксированной длины также фиксированных по длине значений)

 

Задание к лабораторной работе

Студенты, имеющие четный вариант по журналу, реализуют шифрование файлов с помощью алгоритма RSA.

Студенты, имеющие нечетный вариант по журналу, реализуют ЭЦП на базе RSA.

Контрольные вопросы к лабораторной работе:

1. Какие асимметричные алгоритмы шифрования Вы знаете?

2. Какие системы асимметричные или симметричные являются более криптостойкими, почему?

3. В чем отличие арбитражной электронной цифровой подписи от обычной.

4. Назначение сигнатуры? Использование сигнатурного подхода при реализации ЭЦП.

Лабораторная работа №5

Тема: Стеганографические методы защиты информации.

Цель работы: Изучение стеганографических методов защиты информации. Реализация программы с использованием стеганографических принципов защиты информации.

Аддитивные алгоритмы

Алгоритмы аддитивного внедрения информации заключаются в линейной модификации исходного изображения.

В аддитивных методах внедрения ЦВЗ представляет собой последовательность чисел w_i, которая внедряется в выбранное подмножество пикселей исходного изображения f. Основное и наиболее часто используемое выражение для встраивания информации в этом случае

 

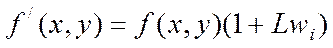          (1)

 

Другой способ встраивания был предложен И.Коксом: 

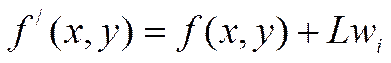(2)

Тут:

- - цвет пикселя с координатами x,y после преобразования

- - цвет пикселя с координатами x,y до преобразования

-L - весовой коэффициент(целое положительное число)

-w(i)-встраиваемое в пиксель x,y число (символ)

 

Цвет пикселя должен представляться в виде одного целого числа.

Нужно отметить, что не все пиксели изображения модифицируются. Модифицируемые пиксели должны быть равномерно распределены по растру изображения. Например, на рисунке показано, как равномерно распределены модифицируемые пиксели по растру размером 5*5. В данном случае в растр «вшивается» информация размером 9 блоков (размер блока рекомендуется брать равным 1-му байту).

 

*		*		*
*		*		*
*		*		*

 

Естественно, размер растра зависит от размеров изображения-контейнера, а количество блоков - от количества «вшиваемой» в изображение информации.

Коэффициент L, рекомендуется изменять по определенному правилу при «вшивании» каждого блока информации. Это повышает устойчивость скрытой информации к дешифрованию.

Имеется массив возможный вариантов коэффициента L.

Правило выборки следующего L определяется правилом выборки следующего элемента массива. Примеры возможных алгоритмов выборки L:

1) прямой порядок;

2) поочередно прямой и обратный порядок выборки;

3) поочередно: L(i), i-четное

                    L(i), i-нечетное

4) L-константа

 

Нестандартный проход выбранных нами для модификации пикселей изображения также увеличивает стойкость алгоритма к дешифрованию. Примеры возможных проходов (в скобках указан порядковый номер пикселя при его модификации («вшивании» информации)):

1) построчный

*(1)		*(2)		*(3)
*(4)		*(5)		*(6)
*(7)		*(8)		*(9)

 

2) зигзагообразный

*(1)		*(2)		*(3)
*(6)		*(5)		*(4)
*(7)		*(8)		*(9)

3) по столбцам

*(1)		*(4)		*(7)
*(2)		*(5)		*(8)
*(3)		*(6)		*(9)

 

 

Примечание:

Рекомендуется в качестве базового формата брать формат, реализующий алгоритм сжатия информации без потерь (например, bmp или pcx). Формат Jpeg не подходит для выполнения работы, т.к. при восстановлении информации из изображения - часть информации теряется или искажается!

Для извлечения скрытой информации необходимо иметь 2 изображения - исходное и то, в которое была записана секретная информация.

Перебираем координаты и сравниваем цвета соответствующих пикселей в изображениях, в случае их несовпадения, мы выявляем пиксели, несущие в себе секретную информацию. Для каждой пары таких пикселей необходимо определить их цвета и выполнить операцию обратную операции преобразования цвета пикселя изображения. Например, для формулы (2) обратная операция будет выглядеть следующим образом:

 

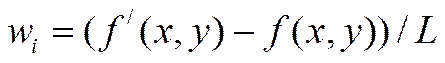
Примечание: способ перебора координат пикселей при сопоставлении цветов зависит от способа прохода пикселей при «вшивании» информации в изображение.

 

2)LSB-алгоритм

Цифровые изображения представляют собой матрицу пикселей. Пиксель – это единичный элемент изображения. Он имеет фиксированную разрядность двоичного представления. Например, пиксели полутонового изображения кодируются 8 битами (значения яркости изменяются от 0 до 255).

Младший значащий бит (LSB) изображения несет в себе меньше всего информации. Известно, что человек обычно не способен заметить изменение в этом бите. Фактически, он является шумом. Поэтому его можно использовать для встраивания информации. Таким образом, для полутонового изображения объем встраиваемых данных может составлять 1/8 объема контейнера. Например, в изображение размером 512х512 можно встроить 32 килобайта информации. Если модифицировать два младших бита (что также почти незаметно), то можно скрытно передать вдвое больший объем данных.

Достоинства рассматриваемого метода заключаются в его простоте и сравнительно большом объеме встраиваемых данных. Однако, он имеет серьезные недостатки. Во-первых, скрытое сообщение легко разрушить. Во-вторых, не обеспечена секретность встраивания информации. Нарушителю точно известно местоположение всего секретного сообщения.

 

Задание к лабораторной работе:

1) Реализовать аддитивный алгоритм (по варианту). Обеспечить возможность как «вшивания» информации (текста) в изображение, так и извлечение секретной информации. Также возможность сохранения и загрузки изображений с жесткого диска.

2) Реализовать алгоритм LSB(по варианту). Требования аналогичные по сравнению с аддитивным алгоритмом.

 

Таблица 5.2 – Варианты заданий к лабораторной работе

 

Вариант	Аддитивный алгоритм			Алгоритм LSB
	Вид аддитивной функции	Способ сканирования изображения	Правило получения следующего L	Число используемых младших бит
1	1	1	1	1
2	2	2	2	1
3	1	3	3	2
4	2	1	4	2
5	1	2	1	1
6	2	3	2	2
7	1	1	3	1
8	2	2	4	1
9	1	3	1	2
10	2	1	2	1
11	1	2	3	2
12	2	3	4	2
13	1	1	1	1
14	2	2	2	2
15	1	3	3	1
16	2	1	4	1
17	1	2	1	2
18	2	3	2	1
19	1	1	3	2
20	2	2	4	2
21	1	3	1	1
22	2	1	2	1
23	1	2	3	2
24	2	3	4	1
25	1	1	1	1
26	2	2	2	2
27	1	3	3	2
28	2	1	4	1
29	1	2	1	2

 

 

Вид аддитивной функции:

1-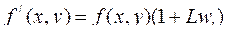

2-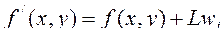

Способ сканирования изображения:

1) построчный

2) зигзагообразный

3) по столбцам

Правило получения следующего L:

1) прямой порядок;

2) поочередно прямой и обратный порядок выборки;

3) поочередно: L(i), i-четное

                    L(i), i-нечетное

4) L-константа

 

Контрольные вопросы к лабораторной работе:

1) Что собой представляет стеганография?

2) Перечислите области применения стеганографических алгоритмов шифрования?

3) Какие способы сканирования изображения Вы знаете?

  4) В чем суть LSB-алгоритма?

  5) От чего зависит криптостойкость стегасистем?

      

Литература

1. В.Столлингс, «Криптография и защита сетей. Принципы и практика», Издательский дом «Вильямс», Москва, С-Петербург, Киев, 2001 г., 669 стр.

2. Соколов А.В., Шаньгин В.Ф., «Защита информации в распределенных корпоративных сетях и системах», ДМК, Москва, 2002 г.

3. Саломаа А. «Криптография с открытым ключем», М.:Мир, 1995 г., 320 стр.

4. Шнайдер Б., «Прикладная криптография. Протоколы, алгоритмы и исходные тексты на языке С»

5. Баричев С., «Криптография без секретов»

6. Дж. Брассард «Современная криптология», 1988 г.

7. Шеннон К. «Теория связи в секретных системах. Примеры секретных систем»

8. Исагулиев К. П., «Справочник по криптологии», 2004 г, 238 стр.

9. Грибунин В.Г., Цифровая стеганография, СОЛОН-Пресс, 2002 можно скачать (http://www.autex.spb.ru/wavelet/books/dstego.htm)

10. Материалы сайта http://www.autex.spb.ru (http://www.autex.spb.ru/wavelet/stego.htm)

11. Генне О.В., Основные положения стеганографии // Защита информации. Конфидент, N3, 2000

Содержание

 

Лабораторная работа №1 «Базовые алгоритмы шифрования»………………...4

Лабораторная работа №2 «Симметричные криптосистемы»……………........29

Лабораторная работа №3 «Однонаправленные хеш-функции в криптографии» ………………………………………………………………..…40

Лабораторная работа №4 «Ассиметричные алгоритмы шифрования. Шифрование данных алгоритмом RSA. Понятия электронно-цифровой подписи. ЭЦП RSA» …………………………………………………………….59

Лабораторная работа №5 «Стеганографические методы защиты информации» …………………………………………………………………….77

Литература ………………………………………………………………………87

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

к лабораторным работам по курсу

«Информационная безопасность»

(для студентов специальности 7.080403 “Программное обеспечение АС”)         

(Часть 1 – Криптографические и стеганографические методы защиты информации)

 

 

Составители:                              Наталия Евгеньевна Губенко

                                                   Алла Викторовна Чернышова

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

к лабораторным работам по курсу

«Информационная безопасность»

(для студентов специальности 7.080403 “Программное обеспечение АС”)         

(Часть 1 – Криптографические и стеганографические методы защиты информации)

 

 

Донецк-ДонНТУ-2013

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

к лабораторным работам по курсу

«Информационная безопасность»

(для студентов специальности 7.080403 “Программное обеспечение АС”)

(Часть 1 – Криптографические и стеганографические методы защиты информации)

 

                                                   Рассмотрено на заседании кафедры

                                              КСМ

                                                                  Протокол № от

Утверждено на заседании

учебно-издательского Совета ДонНТУ

протокол № от  

 

Донецк –2013

УДК 681.3

        

    Методические указания и задания к лабораторным работам по курсу «Информационная безопасность» для студентов специальности «Программное обеспечение АС», часть 1 - «Криптографические и стеганографические методы защиты информации»/ Сост.: Губенко Н.Е., Чернышова А.В. - Донецк, ДонНТУ, 2013 - 89 стр.

 

 

    Приведены методические указания и задания к выполнению лабораторных работ по курсу «Информационная безопасность» для студентов специальности «Программное обеспечение АС». Излагаются вопросы, связанные с криптографическими и стеганографическими методами защиты информации. Рассматриваются простейшие базовые криптоалгоритмы, симметричные и ассиметричные криптосистемы, проверка подлинности информации средствами электронно-цифровой подписи, использование однонаправленных хэш-функций в криптографии, простейшие стеганографические алгоритмы защиты информации.

    Методические указания предназначены для усвоения теоретических основ и формирования практических навыков по курсу «информационная безопасность» по разделу «Криптографические и стеганографические методы защиты информации».

 

Составители:           доцент каф. КСМ, к.т.н. Губенко Н.Е.

                                 Ст.преп. каф. ПМиИ Чернышова А.В.

Рецензент:                   

Лабораторная работа №1

Тема: Базовые алгоритмы шифрования.

Цель: Изучить базовые алгоритмы шифрования и написать программу, выполняющую шифрование текста с помощью одного из базовых алгоритмов, выполнив предварительно модификацию базового алгоритма шифрования.

 Методические указания к лабораторной работе

Рассматриваемые простейшие методы кодирования заключаются в видоизменении информации таким образом, чтобы при попытке ее прочитать, злоумышленник не увидел ничего, кроме бессмысленной последовательности символов, а при попытке подделать или переделать документ, читатель, увидев ту же бессмыслицу, сразу понял бы это. Это и называется шифрованием или криптографией.

Зашифровав текст, его можно переправлять любым доступным способом, но никто не сможет узнать содержимое послания. Хотя, последнее не совсем верно, так как злоумышленник может попытаться раскрыть код.

Наука о раскрытии шифров – криптоанализ – всегда развивалась параллельно шифрованию. В последнее время, обе науки начали опираться на серьезный математический анализ, что только усилило их противоборство.

Не всегда криптоанализ используется злоумышленником. Дело в том, что преступная организация также может зашифровать послание. Тогда, дешифрация сообщения может оказаться жизненно важной. Поэтому, употреблять слово злоумышленник, говоря о шифровании, не совсем корректно, тем более, что в военном конфликте понятия прав и виноват весьма и весьма относительны. Но если сообщение шифруется, всегда есть опасность попытки его дешифрации.

Именно поэтому появился термин криптостойкость, то есть устойчивость алгоритма к криптоанализу.

    Прежде чем говорить о более сложных алгоритмах шифрования, рассмотрим базовые алгоритмы, которые частично используются в современных алгоритмах шифрования. К простейшим алгоритмам шифрования относятся:

- шифр Полибия;

- шифр Цезаря;

- шифр Ришелье;

- перестановочный шифр;

- шифр Виженера;

-    шифр Плейфера;

- шифрование с ключом;

- шифр Вернама;

- шифр «Люцифер»;

Многие криптосистемы, как простые, так и сложные основываются на принципах подставки, перестановки и гаммировании. Прежде чем рассматривать простейшие алгоритмы шифрования опишем в чем суть подстановок, перестановок и гаммирования, так как эти принципы являются базовыми.

Перестановки.

Перестановкой s набора целых чисел (0,1,...,N-1) называется его переупорядочение. Для того чтобы показать, что целое i пере­мещено из позиции i в позицию s(i), где 0 £ (i) < n, будем использовать запись

s=(s(0), s(1),..., s(N-1)).

Число перестановок из (0,1,...,N-1) равно n!=1*2*...*(N-1)*N. Введем обозначение s для взаимно-однозначного отображения (гомо­морфизма) набора S={s₀,s₁, ...,s_N-1}, состоящего из n элементов, на себя.

s: S ® S

s: s_i ® s_s(i), 0 £ i < n

Будем говорить, что в этом смысле s является перестановкой элементов S. И, наоборот, автоморфизм S соответствует пере­становке целых чисел (0,1,2,.., n-1).

Криптографическим преобразованием T для алфавита Z_m называется последовательность автоморфизмов: T={T⁽ⁿ⁾:1£n<¥}

T⁽ⁿ⁾: Z_m,n®Z_m,n, 1£n<¥

Каждое T⁽ⁿ⁾ является, таким образом, перестановкой n-грамм из Z_m,n.

Поскольку T⁽ⁱ⁾ и T^(j) могут быть определены независимо при i¹j, число криптографических преобразований исходного текста размерности n равно (mⁿ)! (Здесь и далее m - объем используемого алфавита.). Оно возрастает непропорционально при увеличении m и n: так, при m=33 и n=2 число различных криптографических преобразований равно 1089!. Отсюда следует, что потенциально существует большое число отображений исходного текста в шифрованный.

Практическая реализация криптогра­фических систем требует, чтобы преобразо­вания {T_k: kÎK} были определены алгоритмами, зависящими от относительно небольшого числа параметров (ключей).

Сис­те­мы под­ста­но­вок.

Определение Подстановкой p на алфавите Z_m называется автоморфизм Z_m, при котором буквы исходного текста t замещены буквами шифрованного текста p(t):

Z_m à Z_m; p: t à p(t).

Набор всех подстановок называется симметрической группой Z_m è будет в дальнейшем обозначаться как SYM(Z_m).

Утверждение SYM(Z_m) c операцией произведения является группой, т.е. операцией, обладающей следующими свойствами:

Замкнутость: произведение подстановок p₁p₂ является подста­новкой:

p: tàp₁(p₂(t)).

Ассоциативность: результат произведения p₁p₂p₃ не зависит от порядка расстановки скобок:

(p₁p₂)p₃=p₁(p₂p₃)

Существование нейтрального элемента: постановка i, опре­деляемая как i(t)=t, 0£t<m, является нейтральным элементом SYM(Z_m) по операции умножения: ip=pi для "pÎSYM(Z_m).

Существование обратного: для любой подстановки p существует единственная обратная подстановка p^-1, удовлетворя­ющая условию

pp^‑1=p^‑1p=i.

Число возможных подстановок в симметрической группе Z_m называется порядком SYM(Z_m) и равно m! .   

Определение. Ключом подстановки k для Z_m называется последовательность элементов симметрической группы Z_m:

k=(p₀,p₁,...,p_n-1,...), p_nÎSYM(Z_m), 0£n<¥

Подстановка, определяемая ключом k, является крипто­гра­фи­ческим преобразованием T_k, при помощи которого осуществляется преоб­разование n-граммы исходного текста (x₀ ,x₁ ,..,x_n-1) в n-грамму шифрованного текста (y₀ ,y₁ ,...,y_n-1):

y_i=p(x_i),   0£i<n

где n – произвольное (n=1,2,..). T_k называется моноалфавитной под­ста­новкой, если p неизменно при любом i, i=0,1,..., в противном случае T_k называется многоалфавитной подстановкой.

Примечание. К наиболее существенным особенностям подста­новки T_k относятся следующие:

1. Исходный текст шифруется посимвольно. Шифрования n-граммы (x₀ ,x₁ ,..,x_n-1) и ее префикса (x₀ ,x₁ ,..,x_s-1) связаны соотношениями

T_k(x₀ ,x₁ ,..,x_n-1)=(y₀ ,y₁ ,...,y_n-1)

T_k(x₀ ,x₁ ,..,x_s-1)=(y₀ ,y₁ ,...,y_s-1)

2. Буква шифрованного текста y_i является функцией только i-й компоненты ключа p_i и i-й буквы исходного текста x_i.

В потоковых шифрах, т. е. при шифровании потока данных, каждый бит исходной информации шифруется независимо от других с помощью гаммирования.

Гаммирование - наложение на открытые данные гаммы шифра (случайной или псевдослучайной последовательности единиц и нулей) по определенному правилу. Обычно используется "исключающее ИЛИ", называемое также сложением по модулю 2 и реализуемое в ассемблерных программах командой XOR. Для расшифровывания та же гамма накладывается на зашифрованные данные.

При однократном использовании случайной гаммы одинакового размера с зашифровываемыми данными взлом кода невозможен (так называемые криптосистемы с одноразовым или бесконечным ключом). В данном случае "бесконечный" означает, что гамма не повторяется.

В некоторых потоковых шифрах ключ короче сообщения. Так, в системе Вернама для телеграфа используется бумажное кольцо, содержащее гамму. Конечно, стойкость такого шифра не идеальна.

Понятно, что обмен ключами размером с шифруемую информацию не всегда уместен. Поэтому чаще используют гамму, получаемую с помощью генератора псевдослучайных чисел (ПСЧ). В этом случае ключ - порождающее число (начальное значение, вектор инициализации, initializing value, IV) для запуска генератора ПСЧ. Каждый генератор ПСЧ имеет период, после которого генерируемая последовательность повторяется. Очевидно, что период псевдослучайной гаммы должен превышать длину шифруемой информации.

Генератор ПСЧ считается корректным, если наблюдение фрагментов его выхода не позволяет восстановить пропущенные части или всю последовательность при известном алгоритме, но неизвестном начальном значении.

При использовании генератора ПСЧ возможно несколько вариантов:

1. Побитовое шифрование потока данных. Цифровой ключ используется в качестве начального значения генератора ПСЧ, а выходной поток битов суммируется по модулю 2 с исходной информацией. В таких системах отсутствует свойство распространения ошибок.

2. Побитовое шифрование потока данных с обратной связью (ОС) по шифртексту. Такая система аналогична предыдущей, за исключением того, что шифртекст возвращается в качестве параметра в генератор ПСЧ. Характерно свойство распространения ошибок. Область распространения ошибки зависит от структуры генератора ПСЧ.

3. Побитовое шифрование потока данных с ОС по исходному тексту. Базой генератора ПСЧ является исходная информация. Характерно свойство неограниченного распространения ошибки.

4. Побитовое шифрование потока данных с ОС по шифртексту и по исходному тексту.

Что­бы по­лу­чить ли­ней­ные по­сле­до­ва­тель­но­сти эле­мен­тов гам­мы, дли­на ко­то­рых пре­вы­ша­ет раз­мер шиф­руе­мых дан­ных, ис­поль­зу­ют­ся дат­чи­ки ПСЧ. На ос­но­ве тео­рии групп бы­ло раз­ра­бо­та­но не­сколь­ко ти­пов та­ких дат­чи­ков.

Конгруэнтные датчики

В на­стоя­щее вре­мя наи­бо­лее дос­туп­ны­ми и эф­фек­тив­ны­ми яв­ля­ют­ся кон­гру­энт­ные ге­не­ра­то­ры ПСП. Для это­го клас­са ге­не­ра­то­ров мож­но сде­лать ма­те­ма­ти­че­ски стро­гое за­клю­че­ние о том, ка­ки­ми свой­ст­ва­ми об­ла­да­ют вы­ход­ные сиг­на­лы этих ге­не­ра­то­ров с точ­ки зре­ния пе­рио­дич­но­сти и слу­чай­но­сти.

Од­ним из хо­ро­ших кон­гру­энт­ных ге­не­ра­то­ров яв­ля­ет­ся ли­ней­ный кон­гру­энт­ный дат­чик ПСЧ. Он вы­ра­ба­ты­ва­ет по­сле­до­ва­тель­но­сти псев­до­слу­чай­ных чи­сел T(i), опи­сы­вае­мые со­от­но­ше­ни­ем

T(i+1) = (A*T(i)+C) mod m,

где А и С - кон­стан­ты, Т(0) - ис­ход­ная ве­ли­чи­на, вы­бран­ная в ка­че­ст­ве по­ро­ж­даю­ще­го чис­ла. Оче­вид­но, что эти три ве­ли­чи­ны и об­ра­зу­ют ключ.

Та­кой дат­чик ПСЧ ге­не­ри­ру­ет псев­до­слу­чай­ные чис­ла с оп­ре­де­лен­ным пе­рио­дом по­вто­ре­ния, за­ви­ся­щим от вы­бран­ных зна­че­ний А и С. Зна­че­ние m обыч­но ус­та­нав­ли­ва­ет­ся рав­ным 2n , где n - дли­на машинного сло­ва в би­тах. Дат­чик име­ет мак­си­маль­ный пе­ри­од М до то­го, как ге­не­ри­руе­мая по­сле­до­ва­тель­ность нач­нет по­вто­рять­ся. По при­чи­не, от­ме­чен­ной ра­нее, не­об­хо­ди­мо вы­би­рать чис­ла А и С та­кие, что­бы пе­ри­од М был мак­си­маль­ным. Как по­ка­за­но Д. Кну­том, ли­ней­ный кон­гру­энт­ный дат­чик ПСЧ име­ет мак­си­маль­ную дли­ну М то­гда и толь­ко то­гда, ко­гда С - не­чет­ное, и А mod 4 = 1.

Для шиф­ро­ва­ния дан­ных с по­мо­щью дат­чи­ка ПСЧ мо­жет быть вы­бран ключ лю­бо­го раз­ме­ра. На­при­мер, пусть ключ со­сто­ит из на­бо­ра чи­сел x(j) раз­мер­но­стью b, где j=1, 2, ..., n. То­гда соз­да­вае­мую гам­му шиф­ра G мож­но пред­ста­вить как объ­е­ди­не­ние не­пе­ре­се­каю­щих­ся мно­жеств H(j).

Шиф­ро­ва­ние с по­мо­щью дат­чи­ка ПСЧ яв­ля­ет­ся до­воль­но рас­про­стра­нен­ным крип­то­гра­фи­че­ским ме­то­дом. Во мно­гом ка­че­ст­во шиф­ра, по­стро­ен­но­го на ос­но­ве дат­чи­ка ПСЧ, оп­ре­де­ля­ет­ся не толь­ко и не столь­ко ха­рак­те­ри­сти­ка­ми дат­чи­ка, сколь­ко ал­го­рит­мом по­лу­че­ния гам­мы. Один из фун­да­мен­таль­ных прин­ци­пов крип­то­ло­ги­че­ской прак­ти­ки гла­сит, да­же слож­ные шиф­ры мо­гут быть очень чув­ст­ви­тель­ны к про­стым воз­дей­ст­ви­ям.

 

Рассмотрим базовые алгоритмы подробнее.

Шифр Полибия.

Самый, пожалуй, древний из всех известных, хотя и не такой распространенный, как шифр Цезаря. Полибий, греческий историк, умер за тридцать лет до появления Цезаря. Суть его метода в том, что составляется прямоугольник (Доска Полибия), например такой, как представлен на рисунке 1.1.

	А	Б	В	Г	Д	Е
А	А	Б	В	Г	Д	Е
Б	Ж	З	И	Й	К	Л
В	М	Н	О	П	Р	С
Г	Т	У	Ф	Х	Ц	Ч
Д	Ш	Щ	Ъ	Ы	Ь	Э
Е	Ю	Я	.	,	-

Рисунок 1.1 – Доска Полибия

Каждая буква может быть представлена парой букв, указывающих строку и столбец, в которых расположена данная буква. Так, представлением букв П, О будут ВГ, ВВ соответственно, а сообщение ШИФР ПОЛИБИЯ зашифруется как ДАБВГВВДЕЕВГВВБЕБВАББВЕБ. Хоть эта система и является более древней, но устойчивость к раскрытию у нее гораздо выше, несмотря на то, что наблюдается увеличение количества символов зашифрованного текста.

Шифр Цезаря.

Первый документально подтвержденный шифр: Гай Юлий Цезарь, желая защитить свои записи, заменял каждую букву следующей по алфавиту. Можно расширить этот алгоритм, поставив в соответствие каждой букве, какую либо другую букву, разумеется, без повторений. Можно даже заменять буквы совершенно сторонними символами, это не повлияет на криптостойкость.

Во времена Цезаря, когда мало кто умел читать, да и статистика не была особенно развитой, такой шифр было почти невозможно взломать. Но теперь этот способ шифрования используют только в качестве головоломок.

Объяснить это легко. Посчитав вхождение каждого символа в тексте, и зная статистические особенности языка, то есть частоту появления каждого символа в текстах, можно смело заменить часть символов на настоящие. Остальной текст можно получить исходя из избыточности текстов на естественных языках. Очевидно также, что шифр Цезаря можно использовать только для текстов.

Это один из самых старых шифров, имеющий ряд серьезных недостатков. Огромное семейство подстановок Цезаря названо по имени римского императора Гая Юлия Цезаря, который поручал Марку Туллию Цицерону составлять послания с использованием 50-буквенного греческого алфавита со сдвигом в 3 знака и дальнейшей подстановкой. Информация об этом дошла к нам от Светония. Попробуем воспроизвести этот метод шифрования для русского алфавита. Для этого создадим таблицу соответствия (рис. 1.2):

Рисунок 1.2 – Пример таблицы соответствия букв русского алфавита

Шифр Ришелье.

Совершенно “естественно” выглядит криптотекст, полученный с помощью криптосистемы Ришелье. Соответственно, защищенность этого алгоритма гораздо выше предыдущих. В основе лежит “замешивание” по определенным законам исходного текста в “мусоре”, или посторонних символах. Зашифрованный текст получается гораздо длиннее исходного, причем эта разница и определяет реальную криптостойкость системы. Суть метода Ришелье в следующем. Создается подобная решетка с прорезями вместо крестов (рис. 1.3):

Х	Х						Х		Х
Х	Х				Х			Х
						Х
Х		Х	Х	Х					Х
							Х		Х
	Х			Х	Х		Х		Х

Рисунок 1.3 – Пример решетки Ришелье

Далее в прорезях отверстий пишется текст, решетка снимается и все оставшееся пространство заполняется “мусором”, затем для усложнения расшифровки криптотекст можно выписать в ряд. Для длинных сообщений этот метод применяется несколько раз. Кстати говоря, выходной криптотекст можно оформить с помощью “мусора” и в виде смыслового послания. Выполнить обратное преобразование в исходный текст можно, зная размер блока и имея аналогичную решетку.

 

Перестановочные шифры.

Этот шифр тоже является одним из первых, он предполагает разбиение текста на блоки, а затем перемешивание символов внутри блока. Это можно сделать разными методами. В первых вариантах этого шифра использовалась таблица, которую заполняли по строкам исходными данными, а зашифрованные данные читали по столбцам.

Криптостойкость этого шифра также оставляет желать лучшего. Дело в том, что филологи уже давно установили, что для прочтения текста не важен порядок букв в слове, достаточно чтобы на месте были первая и последняя буквы слова. Конечно, размер блока не может совпадать с размерами всех слов текста, то есть перемешивание будет более серьезным, но научится читать такой текст не очень сложно.

Рассмотрим этот метод на несложном алгоритме простой столбцевой перестановки. Предварительно условимся, что число столбцов равно пяти. Допустим, имеется текст, который требуется зашифровать: “ПРОСТЫЕ ПЕРЕСТАНОВКИ ВНОСЯТ СУМЯТИЦУ”. Запишем этот текст слева направо, сверху вниз, заполняя последовательно пять столбцов (рис 1.4):

1	2	3	4	5
П	Р	О	С	Т
Ы	Е		П	Е
Р	Е	С	Т	А
Н	О	В	К	И
	В	Н	О	С
Я	Т		С	У
М	Я	Т	И	Ц
У

Рисунок 1.4 – Пример простой столбцевой перестановки

Теперь зададимся ключом, например 35142, и выпишем в ряд столбцы, начиная с третьего, в соответствии с ключом: “О СВН Т ТЕАИСУЦ ПЫРН ЯМУСПТКОСИ РЕЕОВТЯ”. Получилось довольно неплохо. Для расшифровки требуется количество символов зашифрованного текста разделить на 5 и сформировать столбцы в соответствии с ключом.

В итоге получится исходная таблица, из которой можно прочитать текст построчно. Криптостойкость увеличится, если к полученному зашифрованному тексту применить повторное шифрование с другим размером таблицы и ключом или с перестановками не столбцов, а рядов. Перестановочные шифры очень хорошо сочетать с другими, таким образом повышая криптостойкость.

Шифр Виженера.

Наиболее известной и по праву одной из старейших многоалфавитных (одному шифруемому символу соответствует более одного символа) криптосистем является система известного французского криптографа графа Блейза Виженера (1523-1596).

Для преобразования строится алфавитный квадрат с построчным сдвигом символов в каждом последующем ряду (рисунок 1.5)

Рисунок 1.5 – Квадрат Виженера

Далее выбирается ключ. Затем пишется шифруемая фраза, а под ней циклически записывается ключ. Преобразование производится так: шифруемому символу соответствует символ, находящийся на пересечении буквы ключа (столбец) и буквы исходного текста (строка).

Одним и тем же буквам исходного текста соответствуют не всегда одинаковые символы, то есть символы могут принимать различные значения, что является несомненным плюсом в плане криптостойкости зашифрованного текста.

Далее выбирается ключ, например “ГРАФДРАКУЛА”. Затем пишется шифруемая фраза, а под ней циклически записывается ключ. Для примера возьмем фразу “ОТРЯД ЖДЕТ УКАЗАНИЙ” и исключим из нее пробелы:

“ОТРЯДЖДЕТУКАЗАНИЙ” – исходный текст, “ГРАФДРАКУЛАГРАФДР” – циклический ключ. Преобразование производится так: шифруемому символу соответствует символ, находящийся на пересечении буквы ключа (столбец) и буквы исходного текста (строка).

Получим: “СВРУИЦДПЕЮКГЧАБМЩ”. Как видно, одним и тем же буквам исходного текста соответствуют не всегда одинаковые символы, то есть символы могут принимать различные значения, что является несомненным плюсом в плане криптостойкости зашифрованного текста.

Квадрат может быть каким угодно, главное, чтобы он был легко воспроизводимым и левый столбец, так же как и верхний ряд, соответствовали всему алфавиту. В качестве альтернативного варианта это может быть известный квадрат Френсиса Бьюфорта, где строки – зеркальное отражение строк квадрата Виженера. Для усложнения строки могут быть переставлены местами в определенном порядке и т. д. Усложненной разновидностью этого метода является метод шифрования с автоключом, предложенный математиком Дж. Кардано (XVI в.). Суть его в том, что, кроме циклического ключа, есть еще один, записываемый однократно перед циклическим ключом – первичный ключ. Этот нехитрый прием придает дополнительную стойкость алгоритму.

Шифр Плейфейра.

Назван так в честь своего разработчика. Алгоритм заключается в следующем: сначала составляется равносторонний алфавитный квадрат. Для русского алфавита подойдет квадрат 5х6. Задается ключевая фраза без повторов букв, например “БАРОН ЛИС”. Фраза вписывается в квадрат без пробелов, далее последовательно вписываются недостающие буквы алфавита в правильной последовательности. Одну букву придется исключить для выполнения условия равносторонности. Пусть это будет Ъ. Примем допущение, что Ъ=Ь. Итак, получился квадрат, который легко восстановить по памяти:

Теперь условия для преобразования:

1) Текст должен иметь четное количество букв и делиться на биграммы (сочетания по две буквы), недостающую часть текста дополняем самостоятельно одним (любым) символом. Например, текст “ОСЕНЬ” преобразуется в “ОСЕНЬА”.

2) Биграмма не должна содержать одинаковых букв – “СОСНА” – “СО СН АБ”.

Б	А	Р	О	Н
Л	И	С	В	Г
Д	Е	Ж	З	К
М	П	Т	У	Ф
Х	Ц	Ч	Ш	Щ
Ь	Ы	Э	Ю	Я

Рисунок 1.6 – Пример алфавитного квадрата для шифрования методом Плейфера

Правила преобразования:

Если биграмма не попадает в одну строку или столбец, то мы смотрим на буквы в углах прямоугольника, образованного рассматриваемыми буквами. Например: “ДИ” = “ЛЕ”, “ЬУ” = “МЮ” и т. д.

Если биграмма попадает в одну строку (столбец), мы циклично смещаемся на одну букву вправо (вниз). Например, “ЛС”=“ИВ”, “ТЭ”=“ЧР”.

Итак, мы готовы преобразовать текст. Приступим к шифрованию:

“СОВЕЩАНИЕ СОСТОИТСЯ В ПЯТНИЦУ” – первоначально преобразуется в биграммы: “СО ВЕ ЩА НИ ЕС ОС ТО ИТ СЯ ВП ЯТ НИ ЦУ”. Выполнив преобразование по вышеизложенным правилам, получим биграммы: “РВ ЗИ НЦ ГА ИЖ ВР РУ ПС ЭГ УИ ФЭ ГА ПШ”.

Обратите внимание на то, что одинаковые буквы на входе дали разные буквы на выходе криптосистемы, а одинаковые буквы на выходе совсем не соответствуют одинаковым на входе. Таким образом, криптотекст “РВЗИНЦГАИЖВРРУПСЭГУИ” выглядит гораздо более “симпатично”, чем после прямой замены моноалфавитной криптосистемы.

Правила преобразования могут значительно варьироваться. Алфавит может быть упрощен до логического минимума с целью сокращения квадрата. Например, можно переводить текст в транслитерацию и писать латинскими буквами, тогда квадрат будет размером 5х5.

 

Шифрование с ключом.

Этот метод относится к современному периоду.

Текст представляется в двоичном формате, создается двоичный код некоторого размера (ключ), двоичный текст разбивается на блоки того же размера и каждый блок суммируется по модулю два с ключом. Обратное преобразование выполняется тем же методом.

Фактически, это «современный шифр Цезаря», просто подстановка выполняется не посимвольно, а словами. Правда, понятие слова здесь несколько иное – это блок заданной длины.

Криптостойкость этого метода намного выше, чем у предыдущих шифров. Без использования специальных методов криптоанализа его будет очень сложно взломать. Но в настоящее время этот метод используют только для не очень важных документов, так как криптоанализ, в совокупности с современными вычислительными средствами, позволяет не только прочесть текст сообщения, но и во многих случаях получить ключ, что губительно для системы безопасности.

 

Система Вернама.

В 1949 году, Шеннон сформулировал и доказал свою «пессимистическую теорему»: шифр является абсолютно криптостойким тогда и только тогда, когда энтропия ключа больше либо равна энтропии исходного текста. Из теоремы следует, что длина ключа должна быть соразмерна с длиной текста. Если быть более точным, длина ключа должна равняться длине текста.

На основе этой теоремы построена система Вернама. Каждый бит ключа этой системы равновероятно равен 0 либо 1. Длина ключа равна длине текста. Ключ используется только один раз. Доказано, что этот шифр абсолютно не вскрываем. Не будем этого доказывать, но обоснуем.

Для вскрытия шифрованного сообщения необходимо перебрать все возможные комбинации ключей (это единственный способ, так как ключ используется лишь единожды), и среди полученных значений текста выбрать исходный, пусть это будет текст на русском языке. Допустим, что злоумышленник может это сделать мгновенно, то есть опустим временную сложность такой задачи. Для текста любой длины, будет много бессмысленных результатов и их можно отбросить, но злоумышленник получит все возможные тексты заданной длины, в том числе наш текст. Но ничто и никогда не укажет на то, какой из текстов является исходным.

Рассмотрим это на примере четырех буквенных имен. Пусть зашифровано имя «Даша», а ключ «АБВГ». Если используется кодировка ASCII, то зашифрованный текст выглядит следующим образом: ♦!j#. Как говорилось ранее, единственный способ дешифровать текст, полный перебор всех возможных ключей. Но очевидно, что существует такой ключ, суммирование с которым зашифрованного текста даст в результате «Маша», или даже «Миша». Но действительно, невозможно ответить на вопрос, какое из имен является исходным.

Возможно, что аналитик знает часть текста, например, он знает что это договор на продажу недвижимости, но не знает цену. В результате перебора, если на это хватит времени, он получит все возможные цены «заданной длины». То есть если цена трехзначная, аналитиком будет получена девятьсот одна различная цена. Таким образом, взлом системы Вернама не приведет к получению новой информации и является абсолютно невскрываемым.

Недостаток этой системы – длина ключа. Сам Вернам предлагал пересылать ключ курьером. При этом если курьер не довез ключ, можно сгенерировать новый ключ и снова его отправить. Однако такой механизм чрезвычайно неудобен, поэтому эта система не используется в настоящее время.

Этот шифр при его идеальности лишен помехоустойчивости, потому как изменение одного бита, практически невозможно отследить.

 

Шифры, основанные на системе Вернама.

Если мы не можем использовать очень длинный ключ, следует использовать короткий, удлиняя его по некоторому правилу. Было предпринято много попыток создать шифр, как можно более приближенный к системе Вернама.

Первой попыткой было использование ключа в качестве параметров генератора псевдослучайных последовательностей. На деле все системы сводились именно к этому. Но в некоторых случаях ключ получали за счет его преобразований, например, с помощью нелинейной функции.

Рисунок 1.7 - Генерация ключа, для имитации системы Вернама

 

Наиболее удачной была схема, в которой ключ подавался на вход блоку преобразований (рисунок 1.7) одновременно с выходом двоичного счетчика, подключенного к таймеру. Для передачи сообщения правда требовалась большая синхронизация, нежели для системы Вернама, но вполне приемлемая.

 

Шифр «Люцифера».

Этот шифр изначально разрабатывался для аппаратной реализации. Именно при его создании одновременно использовались новейшие достижения в математике и теории кодирования и опыт веков.

«Люцифер» был создан фирмой IBM и долго использовался для внутренних нужд, так как аппаратная реализация системы шифрования имеет некоторые недостатки.

Авторы шифра предложили совместить два основных подхода к шифрованию: подстановки и перестановки.

Сначала, текст разбивается на блоки по n бит. Затем они поступают на вход мультиплексора, который раскладывает блок по модулю 2^n. Биты перемешиваются, и обрабатываются демультиплексором, который собирает биты в блок длиной n бит.

Рисунок 1.8 - Подстановки «Люцифера»

Преимущество таких постановок (Рисунок 1.8) заключается в нелинейности преобразований. По большому счету, можно любой входной поток превратить в любой выходной, но, разумеется, это производится на этапе разработки.

Выполнив подстановку, следует выполнить перестановки. Это делается соответствующей схемой, в которой просто перемешиваются биты (рисунок 1.9).

Рисунок 1.9 - Подстановки «Люцифера»

 

Узнать коммутацию такого блока довольно легко, достаточно подавать ровно одну единицу на вход, и получать ровно одну единицу на выходе. Однако, совместив оба подхода, и создавая как бы несколько итераций, можно очень сильно запутать аналитика (рисунок 1.10).

Легко увидеть, что если на вход подать одну единицу, на выходе получается больше единиц, чем нулей. Криптоаналитик, получивший текст, зашифрованный «Люцифером» будет поставлен в тупик.

 

Рисунок 1.10 - «Люцифер»

 

Для этого шифра очень важно правильно подобрать параметры преобразований обоих типов. Дело в том, что при неудачном выборе параметров преобразований, они могут свестись к простой перестановке, которую легко раскрыть. Поэтому в аппаратную реализацию шифра встроили «сильные параметры.

Однако, аппаратная реализация шифра не позволяет его широкого применения, так как блок подстановок выполняет преобразование, схожее с суммированием с ключом, а суммирование с одним и тем же ключом ставит шифр под удар. С одной стороны, все, кто имеет доступ к системе, знают ключ, поэтому может произойти утечка, с другой стороны, аналитик, получивший достаточно много шифровок сможет таки дешифровать сообщение.

Было несколько попыток избавиться от этого недостатка, но наиболее удачная из них заключалась в том, чтобы каждый блок подстановок заменить двумя, при этом для шифрования, пользователь указывает первый или второй вид подстановок выполнять, создавая двоичный ключ (рисунок 1.11).

Такая реализация шифра была гораздо более криптостойкой и использовалась некоторое время.

 

Рисунок 1.11 - «Люцифер» с ключом

 

Действительно криптостойкий шифр на основе «Люцифера» был предложен в 1973 году Хорстом Фейстелем. Этот алгоритм на самом деле является общим случаем «Люцифера».

Рисунок 1.12 - Классическая сеть Фейстеля

Классическая (или простая) сеть Фейстеля (рисунок 1.12) разбивает исходный текст на блок длиной 2n бит, каждый блок разбивается на два потока L (левый) и R(правый). Далее выполняется преобразование по формуле:

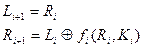
где Ki – ключ, Fi – функция преобразования.

Каждое такое действие называется раундом. Обычно используется 8-16 раундов. При этом, ключ в каждом раунде может быть как частью общего ключа, так и ее модификацией по некоторому правилу: следует отметить, что это в значительной мере влияет на криптостойкость. Также важным является правило, по которому текст разбивается на потоки.

Основное достоинство алгоритма заключается в том, что функция f не обязана быть обратимой, более того, для повышения криптостойкости обычно используют нелинейные именно необратимые функции.

Ключ, с которым суммируется текст не повторяется из блока в блок, а изменяется в зависимости от самого текста, это значительно увеличивает его энтропию, и, следовательно, увеличивает криптостойкость метода.

Процедура расшифровки очевидна, следует применить те же формулы, но в обратном порядке. Некоторые исследователи нашли способ применять один и тот же алгоритм и для шифровки, и для расшифровки, для этого необходимо удвоить число раундов, и во второй половине расположить функции и ключи в обратном порядке. Но как показали эксперименты, криптотойкость при таком подходе значительно ниже.

В последствии были построены сети Фейстеля с большим числом потоков. Это позволило также усложнить подход к функциям преобразования. На рисунке 1.13 представлены примеры таких сетей.

Рисунок 1.13 - Примеры сетей Фейстеля с большим числов потоков

Также существует несколько способов перемешивания: без него, симметричный, асимметричный, - представленные на рисунке 1.14.

Рисунок 1.14 - Способы перемешивания потоков

Сравнивая сети Фейстеля с системой Вернама, становится очевидной высокая помехоустойчивость сетей Фейстеля: если система Вернама при искажении одного бита в зашифрованном тексте, искажала один бит в расшифрованном, то в сети Фейстеля этот бит повлияет на довольно большую часть текста и станет заметным, что позволит выявить случайные или преднамеренные искажения, и переслать шифрованный текст еще раз по другому каналу связи.

В последнее время появились упоминания так называемых Микро Декоррелированных Сетей Фейстеля. Суммируя текст с ключом, криптограф автоматически помещает информацию о ключе в зашифрованный текст, а получение ключа есть конечная цель любого криптоаналитика. Дэвид Вагнер, в своем труде «Атака бумерангом» описал способ уменьшить количество информации в тексте, зашифрованным сетью Фейстеля. Он предложил рассмотреть функции Fi как функции от текста, так, как если бы ключ был частью функции.    

Рассмотрим для примера функцию f(x)=ax+b по одной паре х и f(x) нельзя ничего сказать об а и b. Чем больше пар необходимо, тем лучше такая функция. Но в сетях Фейстеля, криптоаналитик в худшем случае знает исходный текст и зашифрованный тексты, то есть исходные данные и результат последней функции, что делает задачу криптоанализа в случае микро декоррелирующих сетей почти невыполнимой.

Существуют также динамические сети Фейстеля, причем существует несколько их вариантов.

Первый вариант, более простой, предполагает изменение величины блока от раунда к раунду. С одной стороны, это значительно увеличивает время шифрования, так как уже нельзя выбрав блок, сразу полностью произвести все преобразования. С другой стороны, это в значительной мере изменяет статистические характеристики текста. Это легко объяснить тем, что происходит более глубокое перемешивание битов текста. Подстановки в этом случае также несколько отличаются: так как на разных раундах производится подстановка слов различной длины, символы, попадающие в разные блоки, в зависимости от раунда, изменяются по-другому.

Второй вид динамических сетей фейстеля несколько сложнее. Он использует множества отображающих функций – определенное количество функций, по числу блоков, каждая из которых применяется в своем блоке. При этом множество функций изменяется от раунда к раунду. Это изменение также может быть простым перемешиванием, но в идеале, функции не должны повторяться вообще.

Рассматривают также и объединение двух видов динамических сетей Фейстеля. Когда каждый блок суммируется с результатом своей собственной функции, и количество блоков изменяется в зависимости от раунда.

 

 Задание к лабораторной работе

В соответствии с вариантом задания написать программу, реализующую один из базовых алгоритмов шифрования, при этом произвести некоторую модификацию выбранного алгоритма. Программа должна выполнять чтение файла, просмотр, его шифрование, расшифровывание, просмотр зашифрованного расшифрованного документа.

Отчет по лабораторной работе должен включать в себя: Краткое словесное описание базового алгоритма с его частичной модификацией, пример работы алгоритма, листинг программы, результаты работы программы.

Варианты заданий:

    № по журналу                           Базовый алгоритм

- 1-3                                              Шифр Полибия;

- 4-6                                              Шифр Цезаря;

- 7-9                                              Шифр Ришелье;

- 10-12                                                   Перестановочный шифр;

- 13-15                                                   Шифр Виженера

- 16-18                                                   Шифрование с ключем

- 19-21                                                   Шифр Вернама

21 – 25                                       Шифр Плейфейра.

-

Контрольные вопросы к лабораторной работе:

1) Что такое криптоанализ?

2) Что такое криптоскойкость алгоритма?

3) В чем суть перестановочных шифров?

4) В чем суть подстановочных шифров?

5) Назначение гаммирования.

6) Какой из рассмотренных базовых алгоритмов является по Вашему мнению наиболее криптостойким? Объяснить, почему.

7) Как, по Вашему мнению, можно увеличить криптостойкость алгоритма с использованием перестановок?

 

Лабораторная работа №2

Тема: Симметричные криптосистемы.

Цель работы: Изучение принципов шифрования в симметричных криптосистемах. Изучение классов преобразований в симметричных криптосистемах.

Методические указания к выполнению лабораторной работы

Криптографическая система это семейство преобразований шифра и совокупность ключей (т.е. алгоритм + ключи). Само по себе описание алгоритма не является криптосистемой. Только дополненное схемами распределения и управления ключами оно становится системой. Примеры алгоритмов – описания DES, ГОСТ28147-89. Дополненные алгоритмами выработки ключей, они превращаются в криптосистемы. Современные криптосистемы классифицируют следующим образом (рис. 2.1):

Рисунок 2.1 – Классификация криптосистем

Криптосистемы могут обеспечивать не только секретность передаваемых сообщений, но и их аутентичность (подлинность), а также подтверждение подлинности пользователя.

Симметричные криптосистемы (с секретным ключом - secret key systems) данные криптосистемы построены на основе сохранения в тайне ключа шифрования. Процессы зашифрования и расшифрования используют один и тот же ключ. Секретность ключа является постулатом. Основная проблема при применении симметричных криптосистем для связи заключается в сложности передачи обоим сторонам секретного ключа. Симметричные криптосистемы принято подразделять на блочные и поточные.

Блочные криптосистемы разбивают текст сообщения (файла, документа и т.д.) на отдельные блоки и затем осуществляют преобразование этих блоков с использованием ключа.

Поточные криптосистемы работают иначе. На основе ключа системы вырабатывается некая последовательность– так называемая выходная гамма, которая затем накладывается на текст сообщения. Таким образом, преобразование текста осуществляется как бы потоком по мере выработки гаммы.

 

Устройство блочных шифров.

Само преобразование шифра должно использовать следующие принципы (по К. Шеннону):

Рассеивание (diffusion) - т.е. изменение любого знака открытого текста или ключа влияет на большое число знаков шифротекста, что скрывает статистические свойства открытого текста;

Перемешивание (confusion) - использование преобразований, затрудняющих получение статистических зависимостей между шифротектстом и открытым текстом.

Практически все современные блочные шифры являются композиционными - т.е. состоят из композиции простых преобразований или F=F₁oF₂oF₃oF₄o..oF_n, где F - преобразование шифра, F_i - простое преобразование, называемое также i-ым циклом шифрования. Само по себе преобразование может и не обеспечивать нужных свойств, но их цепочка позволяет получить необходимый результат. Например, стандарт DES состоит из 16 циклов. Если же используется одно и то же преобразование, т.е. F_i постоянно для i, то такой композиционный шифр называют итерационным шифром.

Наибольшую популярность имеют шифры, устроенные по принципу шифра Фейстеля (Файстеля - Feistel), в которых:

1. Входной блок для каждого преобразования разбивается на две половины: p=(l,r), где l - левая, a r - правая;

2. Используется преобразование вида F_i (l,r)=(r,l Ä f_i(r)), где f_i– зависящая от ключа K_i функция, а Ä - операция XOR или некая другая.

Функция f_i называется цикловой функцией, а ключ K_i, используемый для получения функции f_i называется цикловым ключом. Как можно заметить, с цикловой функцией складывается только левая половина, а правая остается неизменной. Затем обе половины меняются местами. Это преобразование прокручивается несколько раз (несколько циклов) и выходом шифра является получившаяся в конце пара (l,r) Графически все выглядит следующим образом (рис. 2.2):

Рисунок 2.2 – Пример одного цикла преобразований

В качестве функции f_i выступает некая комбинация перестановок, подстановок, сдвигов, добавлений ключа и прочих преобразований. Так, при использовании подстановок информация проходит через специальные блоки, называемые S-блоками (S-боксами, S-boxes), в которых значение группы битов заменяется на другое значение. По такому принципу (с небольшими отличиями) построены многие алгоритмы: DES, ит.п. В других алгоритмах используются несколько иные принципы. Так, например, алгоритмы, построенные по SP-принципу (SP-сети) осуществляют преобразование, пропуская блок через последовательность подстановок (Substitutions) и перестановок (Permutations). Отсюда и название– SP-сети, т.е. сети "подстановок-перестановок". Примером такого алгоритма является очень перспективная разработка Rijndael. Саму идею построения криптографически стойкой системы путем последовательного применения относительно простых криптографических преобразований была высказана Шенноном (идея многократного шифрования).

Размеры блоков в каждом алгоритме свои. DES использует блоки по 64 бита (две половинки по 32 бита), LOKI97 - 128 бит.

Получение цикловых ключей.

Ключ имеет фиксированную длину. Однако при прокрутке хотя бы 8 циклов шифрования с размером блока, скажем, 128 бит даже при простом прибавлении посредством XOR потребуется 8*128=1024 бита ключа, поскольку нельзя добавлять в каждом цикле одно и то же значение ,так как это ослабляет шифр. Поэтому для получения последовательности ключевых бит придумывают специальный алгоритм выработки цикловых ключей (ключевое расписание - key schedule). В результате работы этого алгоритма из исходных бит ключа шифрования получается массив бит определенной длины, из которого по определенным правилам составляются цикловые ключи. Каждый шифр имеет свой алгоритм выработки цикловых ключей.

Режимы работы блочных шифров.

Чтобы использовать алгоритмы блочного шифрования для различных криптографических задач существует несколько режимов их работы. Наиболее часто встречающимися в практике являются следующие режимы:

­ электронная кодовая книга - ECB (Electronic Code Book);

­ сцепление блоков шифротекста - CBC (Cipher Block Chaining);

­ обратная связь по шифротектсту - CFB (Cipher Feed Back);

­ обратная связь по выходу - OFB (Output Feed Back).

Обозначим применение шифра к блоку открытого текста как E_k(M)=C, где k - ключ, M - блок открытого текста, а C - получающийся шифротекст.

Электронная Кодовая Книга (ECB)

Рисунок 2.3 -  Схема электронной кодовой книги

 

Исходный текст разбивается на блоки, равные размеру блока шифра. Затем каждый блок шифруют независимо от других с использованием одного ключа шифрования (рис.2.3).

Непосредственно этот режим применяется для шифрования небольших объемов информации, размером не более одного блока или для шифрования ключей. Это связано с тем, что одинаковые блоки открытого текста преобразуются в одинаковые блоки шифротекста, что может дать взломщику (криптоаналитику) определенную информацию о содержании сообщения. К тому же, если он предполагает наличие определенных слов в сообщении (например, слово "Здравствуйте" в начале сообщения или "До свидания" в конце), то получается, что он обладает как фрагментом открытого текста, так и соответствующего шифротекста, что может сильно облегчить задачу нахождения ключа.

Основным достоинством этого режима является простота реализации.

Сцепление блоков шифротекста (CBC)

Один из наиболее часто применимых режимов шифрования для обработки больших количеств информации. Исходный текст разбивается на блоки, а затем обрабатывается по следующей схеме (рис.2):

1. Первый блок складывается побитно по модулю 2 (XOR) с неким значением IV – вектором инициализации (Init Vector), который выбирается независимо перед началом шифрования.

2. Полученное значение шифруется.

3. Полученный в результате блок шифротекста отправляется получателю и одновременно служит начальным вектором IV для следующего блока открытого текста.

Рисунок 2.4 - Схема сцепления блоков шифротекста

 

Расшифрование осуществляется в обратном порядке.

В виде формулы, преобразование в режиме CBC можно представить как C_i=E_k(M_i Å C_i-1), где i - номер соответствующего блока. Из-за использования такого сцепления блоков шифротекста с открытым текстом пропадают указанные выше недостатки режима ECB, поскольку каждый последующий блок зависит от всех предыдущих. Если во время передачи один из блоков шифротекста исказится (передастся с ошибкой), то получатель сможет корректно расшифровать предыдущие блоки сообщения. Проблемы возникнут только с этим "бракованным" и следующим блоками. Одним из важных свойств этого режима является "распространение ошибки"– изменение блока открытого текста меняет все последующие блоки шифротекста. Поскольку последний блок шифротекста зависит от всех блоков открытого текста, то его можно использовать для контроля целостности и аутентичности (проверки подлинности) сообщения. Его называют кодом аутентификации сообщения (MAC - Message Authentication Code). Он может защитить как от случайных, так и преднамеренных изменений в сообщениях.

Обратная связь по шифротексту (CFB)

Режим может использоваться для получения поточного шифра из блочного. Размер блока в данном режиме меньше либо равен размеру блока шифра.

             Рисунок 2.5 -  Схема обратной связи по шифротексту

 

Описание работы схемы:

1. IV представляет собой сдвиговый регистр. Вначале IV заполняется неким значением, которое называется синхропосылкой, не является секретным и передается перед сеансом связи получателю.

2. Значение IV шифруется.

3. Берутся первые k бит зашифрованного значения IV и складываются (XOR) с k битами открытого текста. Получается блок шифротекста из k бит.

4. Значение IV сдвигается на k битов влево, а вместо него становится значение ш.т.

5. Затем опять 2 пункт и т.д до конца цикла шифрования.

Расшифрование происходит аналогично.

Особенностью данного режима является распространение ошибки на весь последующий текст. Рекомендованные значения k: 1 <= k <= 8.

Применяется, как правило, для шифрования потоков информации типа оцифрованной речи, видео.

Обратная связь по выходу (OFB)

Данный режим примечателен тем, что позволяет получать поточный шифр в его классическом виде, в отличии от режима CFB, в котором присутствует связь с шифротекстом. Принцип работы схож с принципом работы режима CFB, но сдвиговый регистр IV заполняется не битами шифротекста, а битами, выходящими из-под усечения.

Рисунок 2.6 -  Схема обратной связи по выходу

Расшифрование осуществляется аналогично. То есть, для любого блока длины k операция зашифрования выглядит следующим образом: C_i=M_i Å G_i, где G_i - результат зашифрования некоторого вектора, являющегося заполнением сдвигового регистра. Главное свойство шифра – единичные ошибки не распространяются, т.к. заполнение сдвигового регистра осуществляется независимо от шифротекста.

Область применения: потоки видео, аудио или данных, для которых необходимо обеспечить оперативную доставку. Широко используется у военных наряду с поточными шифрами.

Аутентификация сообщений с помощью блочных шифров.

Аутентификация (authentication – проверка подлинности чего (или кого-)-либо. Может быть аутентификация пользователя, сообщения и т.д. Необходимо отличать ее от следующего понятия:

Идентификация (identification)– некое описательное представление какого-то субъекта. Так, если кто-то заявляет, что он – Вася Иванов, то он идентифицирует себя как "Вася Иванов". Но проверить, так ли это на самом деле (провести аутентификацию) мы можем только при помощи его паспорта.

Итак, как же можно проверить подлинность сообщения с помощью блочного шифра?

Отправитель А хочет отправить некое сообщение (a₁,..,a_t). Он зашифровывает на секретном ключе, который знает только он и получатель, в режиме CBC или CFB это сообщение, а затем, из получившегося шифротекста, берет последний блок b_t из к бит (при этом к должно быть достаточно большим).

1. Отправитель А посылает сообщение (a₁, .. , a_t , b_t ) получателю в открытом виде или зашифровав его на другом ключе.

2. Получатель В, получив сообщение, (a₁, .. , a_t , b_t ), зашифровывает (a₁,..,a_t ) в том же режиме, что и А (должна быть договоренность) на том же секретном ключе (который знает только он и А).

3. Сравнивая полученный результат с b_t он удостоверяется, что сообщение отправил А, что оно не было подделано на узле связи (в случае передачи в открытом виде).

В данной схеме b_t является кодом аутентификации сообщения (МАС). Для российского стандарта шифрования процесс получения кода аутентификации называется работой в режиме имитовставки.

Некоторые комментарии:

Режим шифрования должен быть обязательно с распространением ошибок (т.е. CBC или CFB). Необходимо использовать шифр с достаточной длиной блока, а то может появиться ситуация, когда из-за небольшого числа используемых бит для аутентификации возможно подменить исходное сообщение и при знании ключа получить тот же самый результат. Также очевидно, что схема опирается на то, что оба абонента имеют один и тот же секретный ключ, который получили заранее.

 

 

Задание к лабораторной работе:

1. Изучить алгоритм и разработать программу реализации алгоритма хеш-функции в соответствии с вариантом:

- алгоритм Электронная Кодовая Книга    -

 <номер по журналу > MOD 4 = 0;

- алгоритм Сцепление блоков шифротекста  -

<номер по журналу > MOD 4 = 1;

- алгоритм Обратная связь по шифротексту  -

<номер по журналу > MOD 4 = 2;

- алгоритм Обратная связь по выходу   -

<номер по журналу > MOD 4 = 3

2. Проанализировать алгоритм с точки зрения его безопасности.

 

Контрольные вопросы к лабораторной работе:

1. В чем отличие принципов симметричного и асимметричного шифрования;

2. Каковы основные принципы построения блочных и поточных алгоритмов;

3. В чем принцип рассеивания и перемешивания;

4. Для чего используется вектор инициализации.

 

Лабораторная работа №3

Тема: Однонаправленные хеш-функции в криптографии.

Цель: Изучение алгоритмов построения и использования однонаправленных хеш-функций.

 

Методические указания к выполнению лабораторной работы

Согласно Шнайдеру Б. однонаправленная функция Н(М) применяется к сообщению произвольной длины М и возвращает значение фиксированной длины h , то есть

h = Н(М), где h имеет длину т.

Многие функции позволяют вычислять значение фиксированной длины по входным данным произвольной длины, но у рассматриваемых хэш-функций есть дополнительные свойства, делающие их однонаправленными:

Зная М, легко вычислить h .

Зная Н, трудно определить М, для которого H ( M )= h .

Зная М, трудно определить другое сообщение М’ , для которого Н(М) = Н(М').

То есть смысл однонаправленных хэш-функций и состоит в обеспечении для М уникального идентификатора ("отпечатка пальца"). Если Алиса подписала М с помощью алгоритма цифровой подписи на базе Н(М) , а Боб может создать М', другое сообщение, отличное от М, для которого Н(М) = Н(М'), то Боб сможет утверждать, что Алиса подписала М'.

В ряде приложений однонаправленности недостаточно, необходимо выполнение другого требования, называемого устойчивостью к коллизиям. Его можно сформулировать так: трудно найти два случайных сообщения М и М', для которых Н(М) = Н(М').

Проанализируем протокол, впервые описанный Гидеоном Ювалом, который показывает, как, если предыдущее требование не выполняется, Алиса может использовать вскрытие методом дня рождения для обмана Боба. Он основан не на поиске другого сообщения М, для которого Н(М) = Н(М'), а на поиске двух случайных сообщений, М и М', для которых Н(М) = Н(М') (метод «дней рождений» смотри в Шнайдере раздел7.4).

1. Алиса готовит две версии контракта: одну, выгодную для Боба, и другую, приводящую его к банкротству

2. Алиса вносит несколько незначительных изменений в каждый документ и вычисляет хэш-функции.
(Этими изменениями могут быть действия, подобные следующим : замена ПРОБЕЛА комбинацией ПР О-БЕЛ-ЗАБОЙ-ПРОБЕЛ, вставка одного-двух пробелов перед возвратом каретки, и т.д. Делая или не делая по одному изменению в каждой из 32 строк, Алиса может легко получить 2 ³² различных документов.)

3. Алиса сравнивает хэш-значения для каждого изменения в каждом из двух документов, разыскивая пару, для которой эти значения совпадают. (Если выходом хэш-функции является всего лишь 64-разрядное значение, Алиса, как правило, сможет найти совпадающую пару сравнив 2³² версий каждого документа.) Она
восстанавливает два документа, дающих одинаковое хэш-значение.

4. Алиса получает подписанную Бобом выгодную для него версию контракта, используя протокол, в котором он подписывает только хэш-значение.

5. Спустя некоторое время Алиса подменяет контракт, подписанный Бобом, другим, который он не подписывал. Теперь она может убедить арбитра в том, что Боб подписал другой контракт.

Это серьезная проблема. Одним из советов по ее избежанию является обязательное внесение мелких изменений в подписываемый документ.

При возможности успешного вскрытия этим методом, могут применяться и другие способы вскрытия. Например, противник может посылать системе автоматического контроля (может быть спутниковой) слу­чайные строки сообщений со случайными строками подписей. На каком-то этапе подпись под одним из этих случайных сообщений окажется правильной. Враг не сможет узнать, к чему приведет эта команда, но, если его единственной целью является вмешательство в работу спутника, он своего добьется.