Лабораторная работа № 12
Распространение плоской однородной электромагнитной волны
в однородных средах
(требования к отчету – см. п. 8)
1. Цель работы:
1.1. Научиться рассчитывать параметры электромагнитной (ЭМ) волны.
1.2. Познакомиться с численным методом расчета ЭМ волнового процесса – методом конечных разностей во временной области (FDTD – Finite-Difference Time-Domain).
1.3. Пронаблюдать ЭМ волновой процесс с помощью компьютерного моделирования.
2. Теоретическая подготовка к работе.
Необходимо:
2.1. Повторить материалы лекций по теме работы.
2.2. Изучить определения физических величин и соотношения, описывающие распространение плоской ЭМ волны в однородных средах [1, 2].
2.3. Ознакомиться с методом конечных разностей во временной области [1] и руководством по использованию программы «Максвелл+» [1].
2.4. Подготовить ответы на контрольные вопросы [1].
3. Расчетное задание.
3.1. Определите номер своей бригады и номер варианта задания (совпадает с номером бригады).
3.2. Перепишите из табл. 1 в отчет исходные данные для своего варианта.
3.3. Выполните расчет. В тетради пишите: наименование физической величины; формулу; формулу с подставленными значениями физических величин и обозначениями размерности в системе СИ; результат с обозначением размерности в системе СИ. Пример: 3.3.1. Период изменения напряженности поля: T = 1 / f = 1 / ( 10 ГГц ) = 10–10 с = 100 пс.
Неуказание размерности является ошибкой.
В расчете используйте следующие значения физических констант:
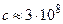м/с – скорость света в свободном пространстве;
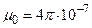Гн/м – абсолютная магнитная постоянная вакуума;
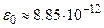Ф/м – абсолютная диэлектрическая постоянная вакуума;
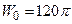Ом » 377 Ом – волновое сопротивление свободного пространства.
При записи значений физических величин используйте множители и приставки:
10–15 = ф (фемто); 10–12 = п (пико); 10–9 = н (нано); 10–6 = мк (микро); 10–3 = м (милли);
103 = к (кило); 106 = М (мега); 109 = Г (гига); 1012 = Т (тера).
Таблица 1. Исходные данные для расчета и численного эксперимента
Параметр
Обозн.
Вариант
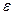
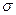
Порядок расчета:
3.3.1. Период колебаний напряженности поля: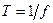 
.
3.3.2. Круговая частота колебаний напряженности поля: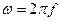 
.
3.3.3. Фазовая скорость волны в среде: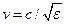 
.
3.3.4. Длина волны в свободном пространстве: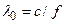 
.
3.3.5. Длина волны в среде: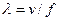 
.
3.3.6. Волновое число в среде: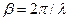 
.
3.3.7. Тангенс угла диэлектрических потерь в среде с потерями: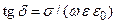 
.
3.3.8. Коэффициент затухания в среде с потерями: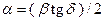 
.
3.3.9. Волновое сопротивление среды-диэлектрика без потерь: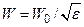 
.
3.3.10. Волновое сопротивление среды-диэлектрика с потерями: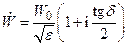 
.
3.3.11. Погонное затухание волны в среде, дБ/м: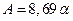 
(значение a – в радиан/м).
3.3.12. Шаг сетки дискретизации пространства: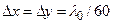 
.
3.3.13. Шаг сетки дискретизации времени: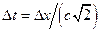 
, результат округлить до единиц пс в меньшую сторону.
3.3.14. Размер области моделирования вдоль О X, ячеек: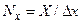 
.
3.3.15. Размер области моделирования вдоль ОY, ячеек: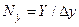 
.
Закончив расчет, предъявите результаты на проверку преподавателю. Если ошибок нет –приступайте к выполнению численного эксперимента.
Подготовка к численному эксперименту.
4.1. Запустите программу электродинамического моделирования «Максвелл+».
Значок программы находится на рабочем столе Windows. В программе используется декартова система координат: начало системы координат – левый верхний угол окнá (окнá рисования, окнá распределения поля); ось OX направлена вправо; ось OY – вниз; ось OZ – перпендикулярно плоскости окна (рис. 1).
Требования к отчету.
Требуется один отчет на бригаду. Отчет принести на следующее занятие и иметь при защите лабораторной работы. В отчете должен быть указан номер группы, фамилии студентов, название лабораторной работы, цель лабораторной работы, формулы и результаты расчетов и измерений, выводы.
Литература
1. Гринев А. Ю, Гиголо А. И. Численное моделирование распространения электромагнитных волн в однородных средах. Учебное пособие. М.: Вузовская книга, 2012.
2. Никольский В. В., Никольская Т. И. Электродинамика и распространение радиоволн: Учебн. пособие для вузов. М.: Наука, 1989.
Лабораторная работа № 12
Распространение плоской однородной электромагнитной волны
в однородных средах
(требования к отчету – см. п. 8)
1. Цель работы:
1.1. Научиться рассчитывать параметры электромагнитной (ЭМ) волны.
1.2. Познакомиться с численным методом расчета ЭМ волнового процесса – методом конечных разностей во временной области (FDTD – Finite-Difference Time-Domain).
1.3. Пронаблюдать ЭМ волновой процесс с помощью компьютерного моделирования.
2. Теоретическая подготовка к работе.
Необходимо:
2.1. Повторить материалы лекций по теме работы.
2.2. Изучить определения физических величин и соотношения, описывающие распространение плоской ЭМ волны в однородных средах [1, 2].
2.3. Ознакомиться с методом конечных разностей во временной области [1] и руководством по использованию программы «Максвелл+» [1].
2.4. Подготовить ответы на контрольные вопросы [1].
3. Расчетное задание.
3.1. Определите номер своей бригады и номер варианта задания (совпадает с номером бригады).
3.2. Перепишите из табл. 1 в отчет исходные данные для своего варианта.
3.3. Выполните расчет. В тетради пишите: наименование физической величины; формулу; формулу с подставленными значениями физических величин и обозначениями размерности в системе СИ; результат с обозначением размерности в системе СИ. Пример: 3.3.1. Период изменения напряженности поля: T = 1 / f = 1 / ( 10 ГГц ) = 10–10 с = 100 пс.
Неуказание размерности является ошибкой.
В расчете используйте следующие значения физических констант:
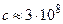м/с – скорость света в свободном пространстве;
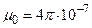Гн/м – абсолютная магнитная постоянная вакуума;
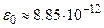Ф/м – абсолютная диэлектрическая постоянная вакуума;
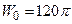Ом » 377 Ом – волновое сопротивление свободного пространства.
При записи значений физических величин используйте множители и приставки:
10–15 = ф (фемто); 10–12 = п (пико); 10–9 = н (нано); 10–6 = мк (микро); 10–3 = м (милли);
103 = к (кило); 106 = М (мега); 109 = Г (гига); 1012 = Т (тера).
Таблица 1. Исходные данные для расчета и численного эксперимента
Параметр
Обозн.
Вариант
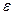
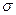
Порядок расчета:
3.3.1. Период колебаний напряженности поля: .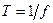
3.3.2. Круговая частота колебаний напряженности поля: .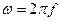
3.3.3. Фазовая скорость волны в среде: .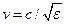
3.3.4. Длина волны в свободном пространстве: .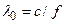
3.3.5. Длина волны в среде: .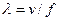
3.3.6. Волновое число в среде: .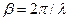
3.3.7. Тангенс угла диэлектрических потерь в среде с потерями: .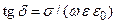
3.3.8. Коэффициент затухания в среде с потерями: .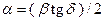
3.3.9. Волновое сопротивление среды-диэлектрика без потерь: .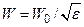
3.3.10. Волновое сопротивление среды-диэлектрика с потерями: .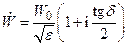
3.3.11. Погонное затухание волны в среде, дБ/м: 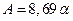(значение a – в радиан/м).
3.3.12. Шаг сетки дискретизации пространства: .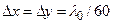
3.3.13. Шаг сетки дискретизации времени: 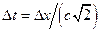, результат округлить до единиц пс в меньшую сторону.
3.3.14. Размер области моделирования вдоль О X, ячеек: .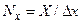
3.3.15. Размер области моделирования вдоль ОY, ячеек: .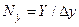
Закончив расчет, предъявите результаты на проверку преподавателю. Если ошибок нет –приступайте к выполнению численного эксперимента.
Подготовка к численному эксперименту.
4.1. Запустите программу электродинамического моделирования «Максвелл+».
Значок программы находится на рабочем столе Windows. В программе используется декартова система координат: начало системы координат – левый верхний угол окнá (окнá рисования, окнá распределения поля); ось OX направлена вправо; ось OY – вниз; ось OZ – перпендикулярно плоскости окна (рис. 1).
Дата: 2019-04-23, просмотров: 226.
