1. Предмет розташований на відстані 15 см від розсіювальної лінзи, з фокусною відстанню 30 см. На якій відстані від лінзи виникає зображення цього предмета? (0,1м)

2. На якій відстані від збиральної лінзи з фокусною відстанню 20 см виникає зображення предмета, якщо сам предмет розташований на відстані 15 см? (0,6 м)

3. На малюнку показано головну оптичну вісь тонкої лінзи, світну точку А та її зображення В. Здійсніть побудовою положення оптичного центру лінзи та її фокусів. Визначте тип лінзи (збиральна чи розсіювальна) і тип зображення (дійсне чи уявне)

       А

М                                                                     N

                                                         B

4. На малюнку показано головну оптичну вісь лінзи і хід одного з променів. Здійсніть побудовою положення фокусів лінзи

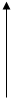
 М

5. На малюнку показано хід променя 1 крізь збиральну лінзу. Побудуйте подальший хід променя 2

Використання алгоритмів не є чимось іншим новим і про їх застосування багато відомо, але цей процес має фрагментальний характер. Так, часто можна зустріти загальний алгоритм розв’язування задач з фізики: прочитати умови задачі, з’ясувати, про яке явище йдеться, записати вихідну формулу, що виражає закономірність перебігу цього явища, вивести кінцеву формулу, підставити числові значення, виконати перевірку на розмірність, записати відповідь або конкретний алгоритм, що вказує, як розв’язувати задачу з тієї чи іншої теми курсу фізики.

Така громісткість алгоритмів та широкий діапазон їх застосування затрюднює їх використання учнями середньої школи. Тому, на думку більшості вчителів, можна вважати, що ефективне застосування алгоритмічного підходу до розв’язування задач пов’язане з тим, що алгоритми треба застосовувати системно (див схему), враховуючи їх властивості: визначеність, масовість та результативність дії.

Елементарний Тематичний Методологічний

 Конкретний

Спочатку (7 клас) пропонуємо елементарний алгоритм

Наприклад, для такої задачі:»Яку площу основи має діжка заввишки 1 м, містить 160 кг бензину? Густина бензину 800кг \ м « ми пропонуємо:

- прочитати умови задачі,

- з’ясувати явище, про яке йдеться

- записати вихідну формулу, що описує це явище,

- вивести кінцеву формулу;

- підставити числові значення і виконати математичні розрахунки

- Записати відповідь

При подальшому вивченні фізики деякі положення цього алгоритму розширюються, конкретизуються. Наприклад, у другому пункті можна додати – « зробити малюнок, зазначивши сили, що діють на тіло», у п’ятому пункті – « перевірити відповідь за розмірністю «. Такий алгоритм легко заповнювати і застосовувати семикласникам, бо має невелику кількість кроків.

Процес розв’язування задачі з фізики пов'язаний з пошуком відповідних закономірностей (законів), що лежать в основі явищ, про які йдеться в задачі, тому наступним етапом перетворення алгоритму є його трансформація в тематичний . Тематичний тип передбачає конкретні дїї. Перетворення елементарного алгоритму у тематичний з конкретним змістом дає змогу учню мати чітке уявлення про методи розв’язування задач з тієї чи іншої теми.       

Так, під час вивчення теплових явищ у 8 класі, розглядаючи задачі на рівняння теплового балансу, використовують такий алгоритм

1 З’ясувати, які тіла беруть участь у теплообміні

2. Визначити, які тіла віддають теплоту, а які – приймають

3 З’ясувати, при яких процесах одні тіла віддують теплоту, а інші приймають ( звернути увагу на температуру)

4. Записати рівняння теплового балансу

5.Розвязати одержане рівняння

Використання такого тематичного алгоритму допомагає учням чітко визначити напрями теплообміну, дає змогу швидко і точно з’ясувати характер процесів, що відображають теплові явища, та скласти рівняння теплового балансу, а вчителю – скоротити час на пояснення задачі

Використовуючи тематичні алгоритми під час вивчення фізики, учні доходять висновку, що розв’язання задач будь-якої зводиться до такої : спочатку уявити фізичне явище чи процес – це означає зробити малюнок, що відображає це явище, потім подумати, як змінюється цей процес за умови задачі (доповнити малюнок), потім пригадати формули чи закони, описують це явище, і нарешті розв’язати одержані рівняння.

Таким чином, алгоритм набуває нових властивостей: він повинен бути простим, коротким, зрозумілим, системним і глибоким за змістом.    Такий підхід до розв’язування задач, коли алгоритм із загальнішого (елементарного) переходить у тематичний, а потім у методологічний (уявити, подумати, згадати, розв’язати), дає можливість учням не лише добре вивчати фізику, розв’язувати задачі, а й пізнавати методи за допомогою яких можна самостійно здобувати знання.

Переходячи від методів, що відображають сприйняття та осмислення явищ, до методів, які сприяють закріпленню, узагальненню і систематизації знань, учень (особливо обдарований), дістає основу для прогнозування подальшого перебігу фізичного явища чи процесу, розвиток абстрактного мислення та інтуїції.