Введение
В настоящее время матричное исчисление широко применяется в различных областях математики, механики, теоретической физики, теоретической электротехники и т.д.
Целью курсовой работы является разработка алгоритма и написание на его основе программы, которая генерирует квадратную матрицу по ее введенному определителю, размерности и диапазона элементов матрицы.
Данная курсовая работа состоит двух глав, включающих в себя каждая несколько параграфов и подпунктов.
В первой главе приведена теоретическая часть по генерации матриц, включающая основные понятия и определения теории матриц, основные теоремы теории матриц, дающие научную основу для разработки алгоритма генерации матриц и написании на его основе программы. Здесь вводятся основные операции над матрицами и детально изучаются свойства определителей, являющихся основой числовой характеристикой квадратных матриц.
Во второй главе рассказывается об основных проблемах, с которыми столкнулся при составлении алгоритма и написании программы, приводится алгоритм генерации матриц, описываются некоторые важные части программы, основывающейся на алгоритме, и приводится листинг программного продукта.
В заключении говорится о проблемах, с которыми столкнулся при составлении алгоритма и написании на его основе программы, и о путях усовершенствования предложенного алгоритма и программы.
Матрицы и определители
Определители
Целью этого параграфа является построение теории определителей любого порядка п.
Рассмотрим произвольную квадратную матрицу любого порядка n:
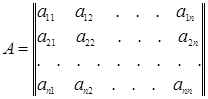 . (1.8)
. (1.8)
С каждой такой матрицей связана определенная численная характеристика, называемая определителем, соответствующим этой матрице.
Если порядок n матрицы (1.8) равен единице, то эта матрица состоит из одного элемента a 11 и определителем первого порядка соответствующим такой матрице, называется величиной этого элемента.
Если далее порядок n матрицы (1.8) равен двум, т.е. если эта матрица имеет вид
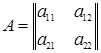 , (1.9)
, (1.9)
то определителем второго порядка, соответствующим такой матрице, есть число, равное a 11 a 22 – a 12 a 21 и обозначаемое одним из символов
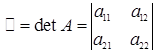 .
.
Итак, по определению
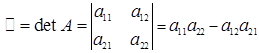 . (1.10)
. (1.10)
Формула (1.10) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.9), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и произведения элементов, стоящих на побочной ее диагонали.
Перейдем теперь к выяснению понятия определителя любого порядка n, где 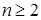 . Понятие такого определителя выводится индуктивно, считая, что понятие определителя порядка n‑1 уже введено, соответствующего произвольной квадратной матрице порядка n‑1.
. Понятие такого определителя выводится индуктивно, считая, что понятие определителя порядка n‑1 уже введено, соответствующего произвольной квадратной матрице порядка n‑1.
Договоримся называть минором любого элемента 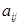 матрицы n ‑го порядка (1.8) определитель порядка n‑1, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания i ‑й строки и j ‑го столбца (той строки и того столбца, на пересечении которых стоит элемент
матрицы n ‑го порядка (1.8) определитель порядка n‑1, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания i ‑й строки и j ‑го столбца (той строки и того столбца, на пересечении которых стоит элемент 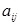 ). Минор элемента
). Минор элемента 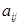 будем обозначать символом
будем обозначать символом 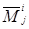 . В этом обозначении верхний индекс обозначает номер строки, нижний – номер столбца, а черта над M означает, что указанные строка и столбец вычеркиваются.
. В этом обозначении верхний индекс обозначает номер строки, нижний – номер столбца, а черта над M означает, что указанные строка и столбец вычеркиваются.
Определителем порядка n, соответствующим матрице (1.8), назовем число, равное 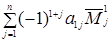 и обозначаемое символом
и обозначаемое символом
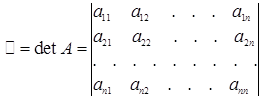 . (1.11)
. (1.11)
Итак, по определению
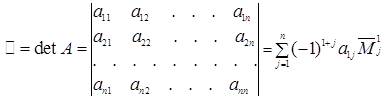 . (1.12)
. (1.12)
Формула (1.12) представляет собой правило составления определителя порядка n по элементам первой строки соответствующей ему матрицы и по минорам 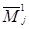 элементов первой строки, являющимся определителями порядка n‑1.
элементов первой строки, являющимся определителями порядка n‑1.
Если n =2, то правило (1.12) в точности совпадает с правилом (1.10), ибо в этом случае миноры элементов первой строки имеют вид: 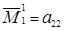 ,
, 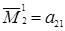 .
.
Естественно возникает вопрос, нельзя ли использовать для получения величины определителя (1.11) элементы и отвечающие им миноры не первой, а произвольной i ‑й строки матрицы (1.8). Ответ на этот вопрос дает следующая основная теорема.
Теорема 1.1. Каков бы ни был номер строки i (i =1,2… n), для определителя n ‑го порядка (1.11) справедлива формула
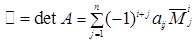 , (1.13)
, (1.13)
называемая разложением этого определителя по i ‑й строке.
В этой формуле показатель степени, в которую возводится число (–1), равен сумме номеров строки и столбца, на пересечении которых стоит элемент ai j .
Доказательство теоремы 1.1. Формулу (1.13) нужно доказать лишь для номеров i = 2, 3,…, n. При n = 2 (т.е. для определителя второго порядка) эту формулу нужно доказать лишь для номера i = 2, т.е. при n = 2 нужно доказать лишь формулу
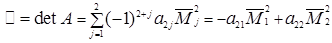
Справедливость этой последней формулы сразу вытекает из выражений для миноров матрицы (1.9) 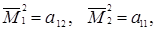 в силу которых правая часть этой формулы совпадает с правой частью (1.10). Итак, при n = 2 теорема доказана.
в силу которых правая часть этой формулы совпадает с правой частью (1.10). Итак, при n = 2 теорема доказана.
Доказательство формулы (1.13) для произвольного n > 2 производится по индукции, т.е. для определителя порядка n – 1 справедлива формула вида (1.13) разложения по любой строке, и, опираясь на это, можно убедиться в справедливости формулы (1.13) для определителя порядка n .
При доказательстве понадобится понятие миноров матрицы (1.8) порядка n – 2. Определитель порядка n‑2, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания двух строк с номерами 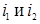 и двух столбцов с номерами
и двух столбцов с номерами 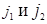 , называется минором (n‑2) – го порядка и обозначается символом
, называется минором (n‑2) – го порядка и обозначается символом 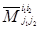 .
.
Определитель n‑го порядка ∆ вводится формулой (1.12), причем в этой формуле каждый минор 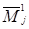 является определителем порядка n‑1, для которого по предположению справедлива формула вида (1.13) разложения по любой строке.
является определителем порядка n‑1, для которого по предположению справедлива формула вида (1.13) разложения по любой строке.
Фиксировав любой номер i (i =2,3… n), разложим в формуле (1.12) каждый минор 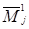 по i – й строке основного определителя (1.11) (в самом миноре
по i – й строке основного определителя (1.11) (в самом миноре 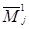 эта строка будет (i‑1) – й).
эта строка будет (i‑1) – й).
В результате весь определитель ∆ окажется представленным в виде некоторой линейной комбинации миноров (n‑2) – го порядка 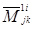 с несовпадающими номерами j и k , т.е. в виде
с несовпадающими номерами j и k , т.е. в виде
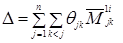 (1.14)
(1.14)
Для вычисления множителей 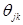 заметим, что минор
заметим, что минор 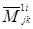 получается в результате разложения по (i‑1) – й строке только следующих двух миноров (n – 1) – го порядка, отвечающих элементам первой строки матрицы (1.8): минора
получается в результате разложения по (i‑1) – й строке только следующих двух миноров (n – 1) – го порядка, отвечающих элементам первой строки матрицы (1.8): минора 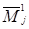 и минора
и минора 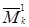 (ибо только эти два минора элементов первой строки содержат все столбцы минора
(ибо только эти два минора элементов первой строки содержат все столбцы минора 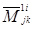 ).
).
В разложениях миноров 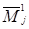 и
и 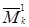 по указанной (i – 1) – й строке выписываются только слагаемые, содержащие минор
по указанной (i – 1) – й строке выписываются только слагаемые, содержащие минор 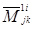 (остальные слагаемые обозначаются многоточием). Учитывая при этом, что элемент ajk минора
(остальные слагаемые обозначаются многоточием). Учитывая при этом, что элемент ajk минора 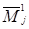 стоит на пересечении (i – 1) – й строки и (k – 1) – го столбца этого минора, а элемент aij минора
стоит на пересечении (i – 1) – й строки и (k – 1) – го столбца этого минора, а элемент aij минора 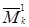 стоит на пересечении (i – 1) – й строки и j‑го столбца этого минора, в итоге получается
стоит на пересечении (i – 1) – й строки и j‑го столбца этого минора, в итоге получается
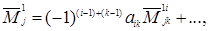 (1.15)
(1.15)
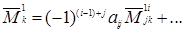 (1.16)
(1.16)
Вставляя (1.15)_ и (1.16) в правую часть (1.12) и собирая коэффициент при 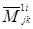 , мы получим, что множитель
, мы получим, что множитель 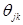 в равенстве (1.14) имеет вид
в равенстве (1.14) имеет вид
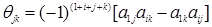 (1 17)
(1 17)
Для завершения доказательства теоремы видно, что и правая часть (1.13) равна сумме, стоящей в правой части (1.14), с теми же самыми значениями (1.17) для 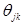 .
.
Для этого в правой части (1.13) разложим каждый минор (n‑1) – го порядка 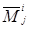 по первой строке. В результате вся правая часть (1.13) представится в виде линейной комбинации с некоторыми коэффициентами
по первой строке. В результате вся правая часть (1.13) представится в виде линейной комбинации с некоторыми коэффициентами 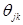 тех же самых миноров
тех же самых миноров 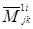
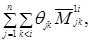 (1.18)
(1.18)
и остается вычислить множители 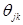 и убедиться в справедливости для них формулы (1.17).
и убедиться в справедливости для них формулы (1.17).
Для этого заметно, что минор 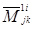 получается в результате разложения по первой строке только следующих двух миноров (n – 1) – го порядка, отвечающих элементам i‑й строки матрицы (1.8): минора
получается в результате разложения по первой строке только следующих двух миноров (n – 1) – го порядка, отвечающих элементам i‑й строки матрицы (1.8): минора 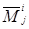 и минора
и минора 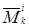 (ибо только эти два минора элементов i‑й строки содержат все столбцы минора
(ибо только эти два минора элементов i‑й строки содержат все столбцы минора 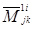 ).
).
В разложениях миноров 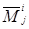 и
и 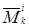 по первой строке выписывается только слагаемые, содержащие минор
по первой строке выписывается только слагаемые, содержащие минор 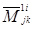 (остальные слагаемые обозначаются многоточием). Учитывая при этом, что элемент aik минора
(остальные слагаемые обозначаются многоточием). Учитывая при этом, что элемент aik минора 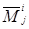 стоит на пересечении первой строки и (k‑1) – го столбца этого минора, а элемент aij минора
стоит на пересечении первой строки и (k‑1) – го столбца этого минора, а элемент aij минора 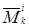 стоит на пересечении первой строки и j ‑го столбца этого минора, получается
стоит на пересечении первой строки и j ‑го столбца этого минора, получается
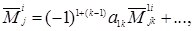 (1.19)
(1.19)
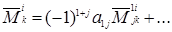 (1.20)
(1.20)
Вставляя (1.19) и (1.20) в правую часть (1.13) и собирая коэффициент при 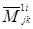 , получается, что
, получается, что 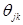 в сумме (1.18) определяется той же самой формулой (1.17), что и в равенстве (1.14).
в сумме (1.18) определяется той же самой формулой (1.17), что и в равенстве (1.14).
Теорема 1.1 доказана.
Теорема 1.1 установила возможность разложения определителя n‑го порядка по любой его строке. Естественно возникает вопрос о возможности разложения определителя n – го порядка по любому его столбцу. Положительный ответ на этот вопрос дает следующая основная теорема.
Теорема 1.2. Каков бы ни был номер столбца j (j =1,2,…, n), для определителя n ‑го порядка (1.11) справедлива формула
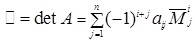 (1.21)
(1.21)
называемая разложением этого определителя по j ‑му столбцу.
Доказательство. Достаточно доказать теорему для j = 1, т.е. установить формулу разложения по первому столбцу
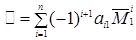 , (1.22)
, (1.22)
иначе если формула (1.22) будет установлена, то для доказательства формулы (1.21) для любого j =2,3,…, n достаточно, поменяв ролями строки и столбцы, дословно повторить схему рассуждений теоремы 1.1.
Формула (1.22) устанавливается по индукции.
При n = 2 эта формула проверяется элементарно (так как при n = 2 миноры элементов первого столбца имеют вид 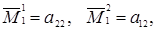 то при n = 2 правая часть (1.22) совпадает с правой частью (1.10)).
то при n = 2 правая часть (1.22) совпадает с правой частью (1.10)).
Предположим, что формула разложения по первому столбцу (1.22) верна для определителя порядка n – 1 и, опираясь на это, можно убедиться в справедливости этой формулы для определителя порядка n .
С этой целью выделим в правой части формулы (1.12) для определителя n – го порядка ∆ первое слагаемое 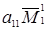 , а в каждом из остальных слагаемых разложим минор (n‑1) – го порядка
, а в каждом из остальных слагаемых разложим минор (n‑1) – го порядка 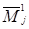 по первому столбцу.
по первому столбцу.
В результате формула (1.12) будет иметь вид
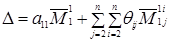 , (1.23)
, (1.23)
где 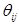 – некоторые подлежащие определению коэффициенты. Для вычисления
– некоторые подлежащие определению коэффициенты. Для вычисления 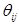 минор
минор 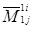 получается при разложении по первому столбцу только одного из миноров (n‑1) – го порядка, отвечающих первой строке, – минора
получается при разложении по первому столбцу только одного из миноров (n‑1) – го порядка, отвечающих первой строке, – минора 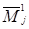 . В разложении минора
. В разложении минора 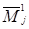 (при
(при 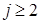 ) по первому столбцу записывается только то слагаемое, которое содержит минор
) по первому столбцу записывается только то слагаемое, которое содержит минор 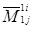 (остальные слагаемые обозначаются многоточием). Учитывая, что элемент ai1 минора
(остальные слагаемые обозначаются многоточием). Учитывая, что элемент ai1 минора 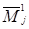 (при
(при 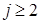 ) стоит на пересечении (i‑1) – й строки и первого столбца этого минора, получается, что при
) стоит на пересечении (i‑1) – й строки и первого столбца этого минора, получается, что при 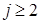
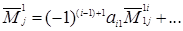 (1.24)
(1.24)
Вставляя (1.24) в правую часть (1.12) (из которой исключено первое слагаемое) и собирая коэффициент при 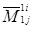 , видно,
, видно,
что коэффициент 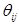 в формуле (1.23) имеет вид
в формуле (1.23) имеет вид
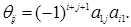 (1.25)
(1.25)
Остается доказать, что и правая часть (1.22) равна сумме, стоящей в правой части (1.23) с теми же самыми значениями (1.25) для 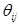 .
.
Для этого в правой части (1.22) выделяется первое слагаемое 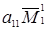 , а в каждом из остальных слагаемых раскладывается минор (n‑1) – го порядка
, а в каждом из остальных слагаемых раскладывается минор (n‑1) – го порядка 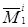 по первой строке.
по первой строке.
В результате правая часть (1.22) представится в виде суммы первого слагаемого 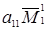 и линейной комбинацией с некоторыми коэффициентами
и линейной комбинацией с некоторыми коэффициентами 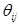 миноров (n‑2) – го порядка
миноров (n‑2) – го порядка 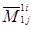 , т.е. в виде
, т.е. в виде
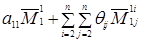 , (1.26)
, (1.26)
и остается вычислить множители 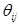 и убедиться в справедливости для них формулы (1.25).
и убедиться в справедливости для них формулы (1.25).
Для этого можно заметить, что минор 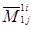 получается в результате разложения по первой строке только одного из миноров n – 1‑го порядка, отвечающих первому столбцу, – минора
получается в результате разложения по первой строке только одного из миноров n – 1‑го порядка, отвечающих первому столбцу, – минора 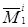 . В разложении минора
. В разложении минора 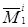 (при
(при 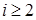 ) по первой строке записывается только то слагаемое, которое содержит минор
) по первой строке записывается только то слагаемое, которое содержит минор 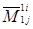 (остальные слагаемые обозначаются многоточием). Учитывая, что элемент
(остальные слагаемые обозначаются многоточием). Учитывая, что элемент 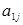 минора
минора 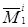 стоит на пересечении первой строки и (j‑1) – го столбца этого минора, получается, что при
стоит на пересечении первой строки и (j‑1) – го столбца этого минора, получается, что при 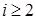
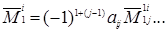 (1.27)
(1.27)
Вставляя (1.24) в правую часть (1.22), из которой исключено первое слагаемое, и собирая коэффициент при 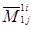 , следует, что
, следует, что 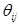 в сумме (1.26) определяется той же самой формулой (1.25), что и в равенстве (1.23). Теорема 1.2 доказана.
в сумме (1.26) определяется той же самой формулой (1.25), что и в равенстве (1.23). Теорема 1.2 доказана.
Выражение определителя непосредственно через его элементы. Установим формулу, выражающую определитель n‑го порядка непосредственно через его элементы (минуя миноры).
Пусть каждое из чисел 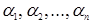 принимает одно из значений 1, 2, …, n, причем среди этих чисел нет совпадающих (в таком случае говорят, что числа
принимает одно из значений 1, 2, …, n, причем среди этих чисел нет совпадающих (в таком случае говорят, что числа 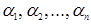 являются некоторой перестановкой чисел 1, 2, …, n). Образуем из чисел
являются некоторой перестановкой чисел 1, 2, …, n). Образуем из чисел 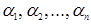 все возможные пары
все возможные пары 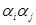 и можно говорить, что пара
и можно говорить, что пара 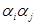 образует беспорядок, если
образует беспорядок, если 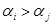 при i<j. Общее число беспорядков, образованных всеми парами, которые можно составить из чисел
при i<j. Общее число беспорядков, образованных всеми парами, которые можно составить из чисел 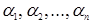 , обозначим символом
, обозначим символом 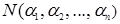 .
.
С помощью метода индукции установим для определителя n‑го порядка (1.11) следующую формулу:
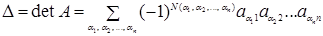 (1.28)
(1.28)
(суммирование в этой формуле идет по всем возможным перестановкам 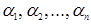 чисел 1, 2, …, n; число этих перестановок, очевидно, равно n!).
чисел 1, 2, …, n; число этих перестановок, очевидно, равно n!).
В случае n =2 формула (1.28) элементарно проверяется (в этом случае возможны только две перестановки 1, 2 и 2, 1, и, поскольку N (1, 2)=0, N (2, 1) = 1, формула (1.28) переходит в равенство (1.10)).
С целью проведения индукции предположим, что формула (1.28) при n>2 справедлива для определителя порядка (n‑1).
Тогда, записав разложение определителя п-го порядка (1.11) по первому столбцу:
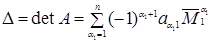 , (1.29)
, (1.29)
можно, в силу предположения индукции, представить каждый минор (n‑1) – го порядка 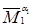 в виде
в виде
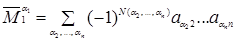 (1.30)
(1.30)
(суммирование идет по всем возможным перестановкам 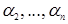 (n – 1) чисел, в качестве которых берутся все натуральные числа от 1 до n, за исключением числа
(n – 1) чисел, в качестве которых берутся все натуральные числа от 1 до n, за исключением числа 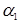 ).
).
Так как из чисел 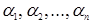 , кроме пар, образованных из чисел
, кроме пар, образованных из чисел 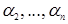 , можно образовать еще только следующие пары
, можно образовать еще только следующие пары 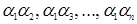 , и поскольку среди чисел
, и поскольку среди чисел 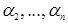 , найдется ровно (
, найдется ровно ( 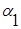 –1) чисел, меньших числа
–1) чисел, меньших числа 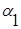 , то
, то 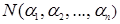 =
= 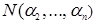 +
+ 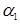 -1.
-1.
Отсюда вытекает, что 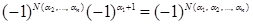 и, вставляя (1.30) в (1.29), получается формула (1.28). Тем самым вывод формулы (1.28) завершен.
и, вставляя (1.30) в (1.29), получается формула (1.28). Тем самым вывод формулы (1.28) завершен.
Теорема Лапласа. В этом пункте устанавливается формула, обобщающая формулу разложения определителя n‑го порядка по какой-либо его строке.
С этой целью вводится в рассмотрение миноры матрицы n – го порядка (1.8) двух типов.
Пусть k – любой номер, меньший n, a 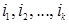 и
и 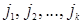 – произвольные номера, удовлетворяющие условиям
– произвольные номера, удовлетворяющие условиям 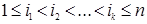 ,
, 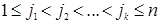 .
.
Миноры первого типа 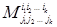 являются определителями порядка k , соответствующими той матрице, которую образуют элементы матрицы (1.8), стоящие на пересечении k строк с номерами
являются определителями порядка k , соответствующими той матрице, которую образуют элементы матрицы (1.8), стоящие на пересечении k строк с номерами 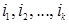 и k столбцов с номерами
и k столбцов с номерами 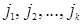 .
.
Миноры второго типа 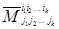 являются определителями порядка n–k , соответствующими той матрице, которая получается из матрицы (1.8) в результате вычеркивания k строк с номерами
являются определителями порядка n–k , соответствующими той матрице, которая получается из матрицы (1.8) в результате вычеркивания k строк с номерами 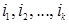 и k столбцов с номерами
и k столбцов с номерами 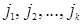 .
.
Миноры второго типа естественно назвать дополнительными по отношению к минорам первого типа.
Теорема 1.3 (теорема Лапласа). При любом номере k , меньшем n , и при любых фиксированных номерах строк 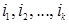 таких, что
таких, что 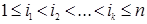 , для определителя n ‑го порядка (1.11) справедлива формула
, для определителя n ‑го порядка (1.11) справедлива формула
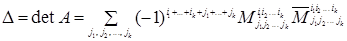 , (1.31)
, (1.31)
называемая разложением этого определителя по k строкам 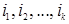 . Суммирование в этой формуле идет по всем возможным значениям индексов
. Суммирование в этой формуле идет по всем возможным значениям индексов 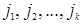 , удовлетворяющим условиям
, удовлетворяющим условиям 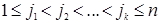 .
.
Доказательство. Прежде всего формула (1.31) является обобщением уже доказанной формулы разложения определителя n‑го порядка по одной его строке с номером i1, в которую она переходит при k = 1 (при этом минор 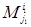 совпадает с элементом
совпадает с элементом 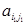 , а минор
, а минор 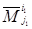 – это введенный выше минор элемента
– это введенный выше минор элемента 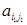 ).
).
Таким образом, при k = 1 формула (1.31) доказана. Доказательство этой формулы для любого k, удовлетворяющего неравенствам 1 < k < n, проводится по индукции, т.е. формула (1.31) справедлива для (k‑1) строк, и, опираясь на это, убедимся в справедливости формулы (1.31) для k строк.
Итак, пусть 1 < k < n и фиксированы какие угодно k строк матрицы (1.8) с номерами 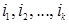 , удовлетворяющими условию
, удовлетворяющими условию 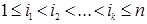 . Тогда по предположению для (k‑1) строк с номерами
. Тогда по предположению для (k‑1) строк с номерами 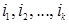 справедлива формула
справедлива формула
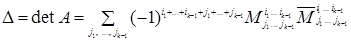 (1.32)
(1.32)
(суммирование идет по всем возможным значениям индексов 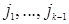 удовлетворяющим условиям
удовлетворяющим условиям 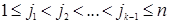 .
.
Разложим в формуле (1.32) каждый минор 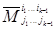 по строке, имеющей в матрице (1.8) номер ik . В результате весь определитель ∆ будет представлен в виде некоторой линейной комбинации миноров
по строке, имеющей в матрице (1.8) номер ik . В результате весь определитель ∆ будет представлен в виде некоторой линейной комбинации миноров 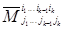 коэффициентами, которые мы обозначим через
коэффициентами, которые мы обозначим через 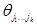 , т.е. для ∆ будет справедливо равенство
, т.е. для ∆ будет справедливо равенство
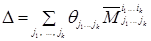 ,
,
и остается вычислить коэффициенты 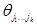 и убедиться в том, что они равны
и убедиться в том, что они равны
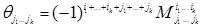 . (1.33)
. (1.33)
С этой целью заметно, что минор (n–k) – го порядка 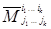 получается в результате разложения по строке с номером ik только следующих k миноров (n–k+1) – го порядка:
получается в результате разложения по строке с номером ik только следующих k миноров (n–k+1) – го порядка:
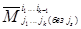 (
( 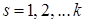 ), (1.34)
), (1.34)
ибо каждый из остальных содержащих строку is миноров (n–k+1) – го порядка не содержит всех строк и всех столбцов минора 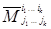 .
.
В разложении каждого минора (1.34) по строке матрицы (1.8) с номером ik выписывается только то слагаемое, которое содержит минор 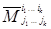 (остальные слагаемые обозначаются многоточием). Учитывая при этом, что в каждом миноре (1.34) элемент
(остальные слагаемые обозначаются многоточием). Учитывая при этом, что в каждом миноре (1.34) элемент 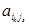 стоит на пересечении [ik – (k‑1)] – й строки и [js – (s‑1)] – го столбца этого минора, получим
стоит на пересечении [ik – (k‑1)] – й строки и [js – (s‑1)] – го столбца этого минора, получим
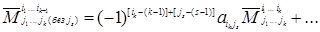
Теперь остается учесть, что в формуле (1.32) каждый минор (1.34) умножается на множитель
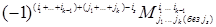
и после этого суммируется по всем s от 1 до k . Имея также в виду, что 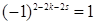 , получаем, что
, получаем, что
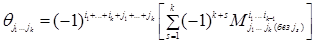 .
.
Замечая, что сумма в квадратных скобках представляет собой разложение минора 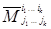 последней k‑й строке, в итоге получим для
последней k‑й строке, в итоге получим для 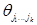 формулу (1.33). Теорема Лапласа доказана.
формулу (1.33). Теорема Лапласа доказана.
В полной аналогии с формулой (1.32) записывается и выводится формула разложения определителя по каким-либо k его столбцам.
Свойства определителей. Ниже устанавливается ряд свойств, которыми обладает произвольный определитель n‑го порядка.
Свойство равноправности строк и столбцов. Транспонированием любой матрицы или определителя называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате транспонирования матрицы A получается матрица, называемая транспонированной по отношению к матрице A и обозначаемая символом A'.
В дальнейшем мы договоримся символом |A|, |B|, |A'|… обозначать определители квадратных матриц A, B, A'… соответственно.
Первое свойство определителя формулируется так: при транспонировании величина определителя сохраняется, т.е. |А'|=|А|.
Это свойство непосредственно вытекает из теоремы 1.2 (достаточно лишь заметить, что разложение определителя |A| по первому столбцу тождественно совпадает с разложением определителя | A' | по первой строке).
Доказанное свойство означает полную равноправность строк и столбцов и позволяет нам все последующие свойства устанавливать лишь для строки быть уверенными в справедливости их и для столбцов.
Свойство антисимметрии при перестановке двух строк (или двух столбцов). При перестановке местами двух строк (или двух столбцов) определитель сохраняет свою абсолютную величину, но меняет знак на противоположный.
Для определителя второго порядка это свойство проверяется элементарно (из правила (1.10) сразу вытекает, что определители
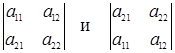
отличаются лишь знаком).
Пусть n > 2, рассмотрим теперь определитель n‑го порядка (1.11) и предположим, что в этом определителе меняются местами две строки с номерами i1 и i 2 . Записывая формулу Лапласа разложения по этим двум строкам, будет иметь
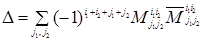 . (1.35)
. (1.35)
При перестановке местами строк с номерами i1 и i2 каждый определитель второго порядка 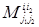 в силу доказанного выше меняет знак на противоположный, а все остальные величины, стоящие под знаком суммы в (1.35), совсем не зависят от элементов строк с номерами i1 и i 2 и сохраняют свое значение. Тем самым свойство 2° доказано.
в силу доказанного выше меняет знак на противоположный, а все остальные величины, стоящие под знаком суммы в (1.35), совсем не зависят от элементов строк с номерами i1 и i 2 и сохраняют свое значение. Тем самым свойство 2° доказано.
Линейное свойство определителя. Будем говорить, что некоторая строка ( 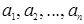 ) является линейной комбинацией строк (
) является линейной комбинацией строк ( 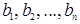 ), (
), ( 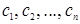 ),…, (
),…, ( 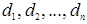 ) с коэффициентами
) с коэффициентами 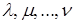 , если
, если 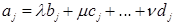 для всех j = 1, 2,…, n .
для всех j = 1, 2,…, n .
Линейное свойство определителя можно сформулировать так: если в определителе n ‑го порядка ∆ некоторая i ‑я строка ( 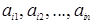 ) является линейной комбинацией двух строк (
) является линейной комбинацией двух строк ( 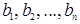 ) и (
) и ( 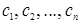 ) с коэффициентами λ и µ, то
) с коэффициентами λ и µ, то 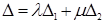 , где
, где 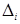 – определитель, у которого i ‑я строка равна (
– определитель, у которого i ‑я строка равна ( 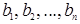 ), а все остальные строки те же, что и у ∆, а ∆2 – определитель, у которого i ‑я строка равна (
), а все остальные строки те же, что и у ∆, а ∆2 – определитель, у которого i ‑я строка равна ( 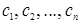 ), а все
), а все
остальные строки те же, что и у ∆.
Для доказательства разложим каждый из трех определителей 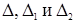 по i‑й строке и заметим, что у всех трех определителей все миноры
по i‑й строке и заметим, что у всех трех определителей все миноры 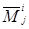 элементов i ‑й строки одинаковы. Но отсюда следует, что формула
элементов i ‑й строки одинаковы. Но отсюда следует, что формула 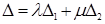 сразу вытекает из равенств
сразу вытекает из равенств 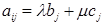 (j = 1, 2,…, n).
(j = 1, 2,…, n).
Конечно, линейное свойство справедливо и для случая, когда i‑я строка является линейной комбинацией не двух, а нескольких строк. Кроме того, линейное свойство справедливо и для столбцов определителя.
Доказанные три свойства являются основными свойствами определителя, вскрывающими его природу.
Следующие пять свойств являются логическими следствиями трех основных свойств.
Следствие 1. Определитель с двумя одинаковыми строками (или столбцами) равен нулю. В самом деле, при перестановке двух одинаковых строк, с одной стороны, определитель ∆ не изменится, а с другой стороны, в силу свойства 2° изменит знак на противоположный. Таким образом, 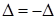 , т.е. 2∆=0 или ∆ = 0.
, т.е. 2∆=0 или ∆ = 0.
Следствие 2. Умножение всех элементов некоторой строки (или некоторого столбца) определителя на число λ равносильно умножению определителя на это число λ.
Иными словами, общий множитель всех элементов некоторой строки (или некоторого столбца) определителя можно вынести за знак этого определителя. (Это свойство вытекает из свойства 3° при μ = 0.)
Следствие 3. Если все элементы некоторой строки (или некоторого столбца) определителя равны нулю, то и сам определитель равен нулю. (Это свойство вытекает из предыдущего при λ = 0.)
Следствие 4. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю. (В самом деле, в силу следствия 2 множитель пропорциональности можно вынести за знак определителя, после чего останется определитель с двумя одинаковыми строками, который равен нулю согласно следствию 1).
Следствие 5. Если к элементам некоторой строки (или некоторого столбца) определителя прибавить соответствующие элементы другой строки (другого столбца), умноженные на произвольный множитель λ, то величина определителя не изменится. (В самом деле, полученный в результате указанного прибавления определитель можно в силу свойства 3° разбить на сумму двух определителей, первый из которых совпадает с исходным, а второй равен нулю в силу пропорциональности двух строк (или столбцов) и следствия 4.)
Следствие 5, как и линейное свойство, допускает более общую формулировку, которую приведем для строк: если к элементам некоторой строки определителя прибавить соответствующие элементы строки, являющейся линейной комбинацией нескольких других строк этого определителя (с какими угодно коэффициентами), то величина определителя не изменится.
Следствие 5 широко применяется при конкретном вычислении определителей (соответствующие примеры будут приведены в следующем пункте).
Прежде чем сформулировать еще одно свойство определителя, введем полезное понятие алгебраического дополнения данного элемента определителя.
Алгебраическим дополнением данного элемента 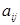 определителя n ‑го порядка (1.11) назовем число, равное
определителя n ‑го порядка (1.11) назовем число, равное 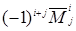 и обозначаемое символом
и обозначаемое символом 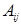 .
.
Таким образом, алгебраическое дополнение данного элемента может отличаться от минора этого элемента только знаком.
С помощью понятия алгебраического дополнения теоремы 1.1 и 1.2 можно переформулировать так: сумма произведений элементов любой строки (любого столбца) определителя на соответствующие алгебраические дополнения этой строки (этого столбца) равна этому определителю.
Соответствующие формулы разложения определителя по i‑й строке и по j‑му столбцу можно переписать так:
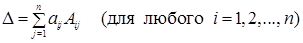 (1.13')
(1.13')
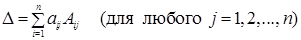 (1.21')
(1.21')
Свойство алгебраических дополнений соседних строк (или столбцов). Сумма произведений элементов какой-либо строки (или какого-либо столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (любого другого столбца) равна нулю.
Доказательство проведем для строк (для столбцов оно проводится аналогично). Записывая подробно формулу (1.13')
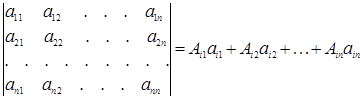 (1.36)
(1.36)
видно, что поскольку алгебраические дополнения 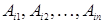 не зависят от элементов i – й строки
не зависят от элементов i – й строки 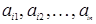 , то равенство (1.36) является тождеством относительно
, то равенство (1.36) является тождеством относительно 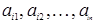 и сохраняется при замене чисел
и сохраняется при замене чисел 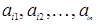 любыми другими n числами. Заменив
любыми другими n числами. Заменив 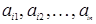 соответствующими элементами любой (отличной от i‑й) k ‑й строки
соответствующими элементами любой (отличной от i‑й) k ‑й строки 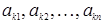 , мы получим слева в (1.36) определитель с двумя одинаковыми строками, равный нулю согласно следствию 1. Таким образом,
, мы получим слева в (1.36) определитель с двумя одинаковыми строками, равный нулю согласно следствию 1. Таким образом,
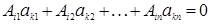
(для любых несовпадающих i и k).
Алгоритм.
1. Ввести определитель, размерность и диапазон значений генерируемой матрицы.
2. Если введенный определитель является простым числом, выходящим за рамки введенного диапазона, и размерность меньше двух, то выдать сообщение об ошибке и перейти к пункту 1, иначе, при корректном вводе, перейти к пункту 3.
3. Организовать функцию разложения определителя на простые множители. Полученные множители записать в вспомогательный массив.
4. Если размерность вспомогательного массива меньше размерности строки генерируемой матрицы, то массив дополняется единицами до тех пор, пока размерность вспомогательного массива не будет равна размерности строки генерируемой матрицы. Если размерность вспомогательного массива больше размерности строки генерируемой матрицы, то получившийся в результате разности размерностей массива и матрицы хвост перемножается с первыми элементами вспомогательного массива.
5. Организовать цикл для генерации матрицы, в которой получившийся массив в пункте 4 располагается на главной диагонали, и одна из областей, находящихся выше или ниже главной диагонали, заполняется случайными числами, принадлежащими введенному диапазону, а другая заполняется нулями.
6. Дальше берется первая строка, умноженная на определенные коэффициенты, получившейся матрицы и складывается с остальными строками.
7. Вывести получившуюся матрицу на экран.
Листинг программы, реализующей алгоритм генерации матриц
#include <conio.h>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
void gen_matric_0 (int *matr, int n, int a, int b);
void gen_matric_1 (int *matr, int n);
void gen_matric (int *matr, int *mas_fakt, int n, int a, int b);
int prov_data (int det, int a, int b, int n);
void print_matric (int *matr, int n);
void faktor (int *mas_fakt, int det, int n);
int prost (int det);
void main()
{
clrscr();
randomize();
FILE *fp;
int *matr, mas[4], det, k,*mas_fakt;
int n, i, j, l, l1, a, b;
int flag;
fp=fopen («inf.txt», «r»);
fseek (fp, 0L, SEEK_END);
l=ftell(fp);
fseek (fp, 0L, SEEK_SET);
printf («Входные данные:\n»);
i=0;
while (l!=ftell(fp))
{
fscanf (fp, «%d»,&k);
l1=ftell(fp);
mas[i]=k;
printf («%d:», mas[i]);
i++;
fseek (fp, l1, SEEK_SET);
}
fclose(fp);
det=mas[0];
n=mas[1];
a=mas[2];
b=mas[3];
matr=(int*) malloc (n*n*sizeof(int));
mas_fakt=(int*) malloc (n*sizeof(int));
faktor (mas_fakt, det, kol, n);
flag=prov_data (det, a, b, n);
if (flag==-1)
printf («\nПроверьте правильность ввода данных!\nРазмерность должна быть > или равно 2.\n Определитель должен входить в диапазон, \n если является простым числом, \n или раскладываться на простые множители принадлежащие данному диапазону!!!»);»);
else if (flag!=-1)
{
printf («\nМатрица:\n»);
if (flag==0)
gen_matric_0 (matr, n, a, b);
else if (flag==1)
{
gen_matric_1 (matr, n);
print_matric (matr, n);
printf («\n или\n\n»);
gen_matric (matr, mas_fakt, n, a, b);
}
else if (flag==2)
gen_matric (matr, mas_fakt, n, a, b);
print_matric (matr, n);
}
free (mas_fakt);
free(matr);
free(kol);
getch();
}
int prov_data (int det, int a, int b, int n)
{
int flag;
if (det<a || det>b)
{
if (prost(det)==1 || n<2)
flag= -1;
}
else if (det==0)
flag= 0;
else if (det==1)
flag= 1;
else if (det>1 || (det<0 && det>a))
flag= 2;
return flag;
}
void gen_matric_0 (int *matr, int n, int a, int b)
{
int *mass;
int nomer_str, i, j, k, l, ras;
mass=(int*) malloc (n*sizeof(int));
ras=n;
nomer_str=0;
if (n==2)
k=1;
else if (n>2)
k=2;
for (l=0; l<ras; l++)
mass[l]=a+random (b-a);
for (i=0; i<n; i++)
for (j=0, l=0; j<n; j++)
{
if (i==nomer_str)
{
*(matr+i*n+j)=mass[l];
l++;
}
else if (i==k)
{
*(matr+i*n+j)=mass[l];
l++;
}
else *(matr+i*n+j)=random (b-a)+a;
}
free(mass);
}
void gen_matric_1 (int *matr, int n)
{
int i, j;
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{
if (i==j)
*(matr+i*n+j)=1;
else if (i!=j)
*(matr+i*n+j)=0;
}
}
void gen_matric (int *matr, int *mas_fakt, int n, int a, int b)
{
int i, j,*vsp_mas, k=1, k1;
vsp_mas=(int*) malloc (n*sizeof(int));
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{
if (i==j)
{
*(matr+i*n+j)=*(mas_fakt+j);
}
else if (i<j)
{
if (a>=-10 && b<=10)
*(matr+i*n+j)=random (b-a)+a; if (a<-10 || b>10)
*(matr+i*n+j)=random (b/4‑a/4)+a/4;
}
else *(matr+i*n+j)=0;
}
for (i=0; i<n; i++)
*(vsp_mas+i)=*(matr+0*n+i);
for (i=0; i<n; i++)
{
if (a<-10 || b>10)
{
k=random(7) – 3;
if (k1==k)
{
if (k<=3 && k>-3)
k-=1;
else if (k>=-3 && k<3)
k+=1;
}
}
for (j=0; j<n; j++)
{
if (i>0)
*(matr+i*n+j)=*(matr+i*n+j)+*(vsp_mas+j)*k;
else if (i==0)
*(matr+i*n+j)=*(matr+i*n+j);
}
k1=k;
}
free (vsp_mas);
}
void print_matric (int *matr, int n)
{
int i, j;
for (i=0; i<n; i++)
{
for (j=0; j<n; j++)
{
printf («%5d»,*(matr+i*n+j));
}
printf («\n»);
}
}
void faktor (int *mas_fakt, int det, int n)
{
int i, j=0, d, r;
int *mass1,*mass2;
mass1=(int*) malloc (n*sizeof(int));
mass2=(int*) malloc (n*sizeof(int));
if (det<0) d=-1*det;
else if (det>=0) d=det;
for (i=2; i<=d; i++)
{
while (d % i==0)
{
d/=i;
*(mas_fakt+j)=i;
j++;
}
}
if (j<n)
{
while (j<=n)
{
*(mas_fakt+j)=1;
j++;
}
}
else if (j>n)
{
r=i=0;
while (i<j)
{
if (i<n)
*(mass1+i)=*(mas_fakt+i);
else if (i>=n)
{
*(mass2+r)=*(mas_fakt+i);
r++;
}
i++;
}
for (i=0; i<r; i++)
{
j=*(mass2+i);
*(mass1+i)=*(mass1+i)*j;
}
for (i=0; i<n; i++)
*(mas_fakt+i)=*(mass1+i);
}
if (det<0)
{r=*(mas_fakt+0);*(mas_fakt+0)=-1*r;}
free(mass1);
free(mass2);
}
int prost (int det)
{
int d, i, flag=1;
d=det;
if((d % 2==0 && d!=0 && d!=2) || d<0)
flag=0;
else
for (i=3; i<sqrt(d); i+=2)
if (d % i==0)
flag=0;
return flag;
Заключение
В заключение данной курсовой работы хотелось бы кратко сказать о проделанной работе, о проблемах, с которыми столкнулся при выполнении поставленной цели, и о перспективах развития и улучшения данного программного продукта.
Целью данной курсовой работы было составить алгоритм генерации матриц по введенному определителю, размерности и диапазона элементов матрицы.
Чтобы выполнить поставленную цель, необходимо было решить три задачи:
1. Поиск литературы по предмету данной курсовой работы.
2. Составление алгоритма для выполнения поставленной цели.
3. Написание программы, реализующей составленный алгоритм.
При решении третьей задачи столкнулся с трудностью проверки корректности ввода данных. Необходимо было проверять, чтобы вводимый определитель удовлетворял диапазону элементов матрицы, т.е. введенный определитель, если является простым числом, то должен входить во введенный диапазон, и размерность матрицы должна быть больше двух.
Основными источниками, помогавшими выполнить поставленную цель, явились:
1. Книги по линейной алгебре, в которых содержался материал по теории матриц.
2. Книги по информатике и программированию.
Результатом данной курсовой работы стал алгоритм генерации матриц и написанная на его основе программа. Данная программа предназначена для работы с целыми числами. Одной из перспектив развития данного алгоритма является его улучшение для работы с действительными и комплексными числами, а программы – написание ее для работы со всеми числами: целыми, вещественными, комплексными.
Чтобы более полно использовать возможности алгоритма, его лучше реализовывать на тех языках программирования, у которых типы данных имеют достаточно большие диапазоны.
Надеюсь, что данная программа из области исследования при выполнении курсовой работы, при условии ее усовершенствования, выйдет в свет как полностью готовый к использованию программный продукт и будет востребован не только в целях методических разработок.
Список литературы
1. Ланкастер П. Теория матриц / Ланкастер П. – М.: Наука, 1982. – 272 с.
2. Линейная алгебра / Ильин В.А., Позняк Э.Г. – М.: Наука, 1978. – 304 с.
3. Кострикин А.И. Введение в алгебру / Кострикин А.И. – М.: Физико-математическая литература, 2001. – 368 с.
4. Писанецки С. Технология разряженных матриц / Писанецки С. – М.: Мир, 1988. – 410 с.
5. Гантмахер Ф.Р. Теория матриц / Гантмахер Ф.Р. – М.: Наука, 1988. – 552 с.
6. Подбельский В.В. Язык С++ / Подбельский В.В. – М.: Финансы и статистика, 2003. – 560 с.
7. Кетков Ю.Л., Кетков А.Ю. Практика программирования: Бейсик, Си, Паскаль. Самоучитель. / Кетков Ю.Л., Кетков А.Ю. – СПб.: БХВ – Петербург, 2002. – 480 с.
8. Мальцев А.И. Основы линейной алгебры / Мальцев А.И. – М.: Наука, 1970. – 400 с.
9. Крячков А.В., Сухинина И.В., Томшин В.К. Программирование на С и С++ / Крячков А.В., Сухинина И.В., Томшин В.К. – М.: Горячая линия – Телеком, 2000. – 344 с.
Приложение
Таблица тестов.
В таблице приведены результаты некоторых тестов программы.
| номер теста | входные данные | выходные данные |
| 1 | 0 2 -100 100 | 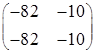
|
| 2 | -10 3 -50 50 | 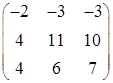
|
| 3 | -1 3 -24 50 | 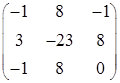
|
| 4 | 50 2 -100 100 | 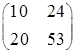
|
| 5 | 113 4 -100 100 | Проверьте правильность ввода данных! Размерность должна быть > или равно 2. Определитель должен входить в диапазон, если является простым числом, или раскладываться на простые множители принадлежащие данному диапазону!!! |
| 6 | 1 3 -24 50 | 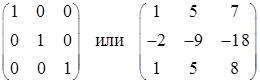
|
Введение
В настоящее время матричное исчисление широко применяется в различных областях математики, механики, теоретической физики, теоретической электротехники и т.д.
Целью курсовой работы является разработка алгоритма и написание на его основе программы, которая генерирует квадратную матрицу по ее введенному определителю, размерности и диапазона элементов матрицы.
Данная курсовая работа состоит двух глав, включающих в себя каждая несколько параграфов и подпунктов.
В первой главе приведена теоретическая часть по генерации матриц, включающая основные понятия и определения теории матриц, основные теоремы теории матриц, дающие научную основу для разработки алгоритма генерации матриц и написании на его основе программы. Здесь вводятся основные операции над матрицами и детально изучаются свойства определителей, являющихся основой числовой характеристикой квадратных матриц.
Во второй главе рассказывается об основных проблемах, с которыми столкнулся при составлении алгоритма и написании программы, приводится алгоритм генерации матриц, описываются некоторые важные части программы, основывающейся на алгоритме, и приводится листинг программного продукта.
В заключении говорится о проблемах, с которыми столкнулся при составлении алгоритма и написании на его основе программы, и о путях усовершенствования предложенного алгоритма и программы.
Матрицы и определители
Матрицы. Действия с матрицами
Все определения, теоремы, свойства, следствия и их доказательства, используемые в курсовой работе, взяты из книги В.А. Ильина, Э.Г. Позняка «Линейная алгебра».
Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов (размера 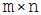 ).
).
Числа m и n называются порядками матрицы. Если m=n, матрица называется квадратной, а число m=n – её порядком.
Для записи матрицы применяются либо сдвоенные черточки, либо круглые или квадратные скобки:
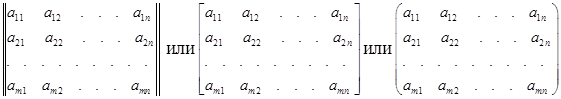
Для краткого обозначения матрицы часто используется либо одна большая латинская буква (например, A), либо символ 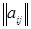 , либо
, либо 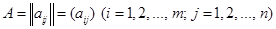 .
.
Числа 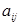 , входящие в состав данной матрицы, называются её элементами. В записи
, входящие в состав данной матрицы, называются её элементами. В записи 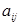 первый индекс
первый индекс 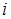 означает номер строки, а второй индекс
означает номер строки, а второй индекс 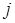 – номер столбца.
– номер столбца.
В случае квадратной матрицы
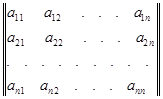 (1.1)
(1.1)
вводится понятия главной и побочной диагоналей. Главной диагональю матрицы называется диагональ a11 a 22 … an n, идущая из левого верхнего угла этой матрицы в правый нижний её угол. Побочной диагональю матрицы называется диагональ an1 a(n -1)2 … a1n, идущая из левого нижнего угла в правый верхний угол.
Прежде всего, будем считать две матрицы равными, если эти матрицы имеют одинаковые порядки и все их соответствующие элементы совпадают.
Перейдём к определению основных операций над матрицами.
Сложение матриц. Суммой двух матриц 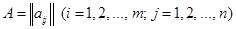 и
и 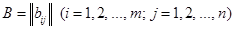 одних и тех же порядков m и n называется матрица
одних и тех же порядков m и n называется матрица 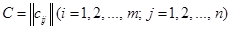 тех же порядков m и n, элементы ci j которой равны
тех же порядков m и n, элементы ci j которой равны
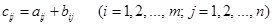 (1.2)
(1.2)
Для обозначения суммы двух матриц используется запись C=A+B. Операция составления суммы матриц называется их сложением.
Итак, по определению
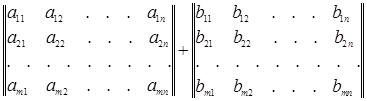 =
=
= 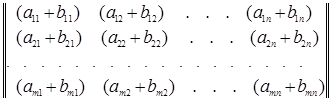
Из определения суммы матриц, а точнее из формулы (1.2) непосредственно вытекает, что и операция сложения матриц обладает теми же свойствами, что и операция сложения вещественных чисел, а именно:
1) переместительным свойством: A+B=B+A,
2) сочетательным свойством: (A+B)+C=A+(B+C).
Эти свойства позволяют не заботиться о порядке следования слагаемых матриц при сложении двух или большего числа матриц.
Умножение матрицы на число. Произведением матрицы 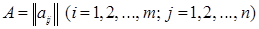 на вещественное число λ называется матрица
на вещественное число λ называется матрица 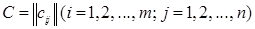 , элементы ci j которой равны
, элементы ci j которой равны
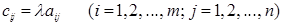 (1.3)
(1.3)
Для обозначения произведения матрицы на число используется запись C=λA или C=Aλ. Операция составления произведения матрицы на число называется умножением матрицы на это число.
Из формулы (1.3) видно, что умножение матрицы на число обладает следующими свойствами:
1) сочетательным свойством относительно числового множителя: (λμ) A = λ(μA);
2) распределительным свойством относительно суммы матриц: λ (A+B) = λA + λB;
3) распределительным свойством относительно суммы чисел: (λ+μ) A = λA + μA.
Замечание. Разностью двух матриц A и B одинаковых порядков m и n естественно назвать такую матрицу C тех же порядков m и n, которая в сумме с матрицей B даёт матрицу A. Для обозначения разности двух матриц используется естественная запись: C = A – B.
Очень легко убедиться, что разность C двух матриц A и B может быть получена по правилу C = A + (– 1) B.
Перемножение матриц. Произведением матрицы 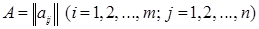 , имеющей порядки, соответственно равные m и n , на матрицу
, имеющей порядки, соответственно равные m и n , на матрицу 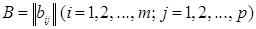 , имеющую порядки, соответственно равные m и p, называется матрица
, имеющую порядки, соответственно равные m и p, называется матрица 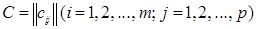 , имеющая порядки, соответственно равные т и р, и элементы ci j , определяемые формулой
, имеющая порядки, соответственно равные т и р, и элементы ci j , определяемые формулой
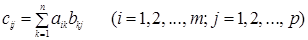 . (1.4)
. (1.4)
Для обозначения произведения матрицы A на матрицу B используют запись 
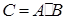 . Операция составления произведения матрицы A на матрицу B называется перемножением этих матриц.
. Операция составления произведения матрицы A на матрицу B называется перемножением этих матриц.
Из сформулированного выше определения вытекает, что матрицу А можно умножить не на всякую матрицу B: необходимо, чтобы число столбцов матрицы A было равно числу строк матрицы B.
В частности, оба произведения 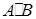 и
и 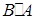 можно определить лишь в том случае, когда число столбцов A совпадает с числом строк B, а число строк A совпадает с числом столбцов B. При этом обе матрицы
можно определить лишь в том случае, когда число столбцов A совпадает с числом строк B, а число строк A совпадает с числом столбцов B. При этом обе матрицы 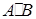 и
и 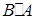 будут квадратными, но порядки их будут различными. Для того чтобы оба произведения
будут квадратными, но порядки их будут различными. Для того чтобы оба произведения 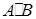 и
и 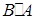 не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка.
не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка.
Формула (1.4) представляет собой правило составления элементов матрицы C, являющейся произведением матрицы A на матрицу B. Это правило можно сформулировать и словесно: элемент cij стоящий на пересечении i ‑й строки и j ‑го столбца матрицы C = 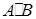 , равен сумме попарных произведений соответствующих элементов i ‑й строки матрицы A и j ‑го столбца матрицы B .
, равен сумме попарных произведений соответствующих элементов i ‑й строки матрицы A и j ‑го столбца матрицы B .
В качестве примера применения указанного правила приведем формулу перемножения квадратных матриц второго порядка
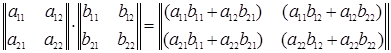 .
.
Из формулы (1.4) вытекают следующие свойства произведения матрицы A на матрицу B:
1) сочетательное свойство: (AB) C = A(BC);
2) распределительное относительно суммы матриц свойство: (A+B) C=AC+BC или A (B+C)=AB+AC.
Распределительное свойство сразу вытекает из формул (1.4) и (1.2), а для доказательства сочетательного свойства достаточно заметить, что если 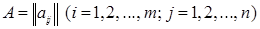 ,
, 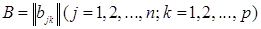 ,
, 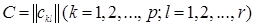 , то элемент
, то элемент 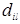 матрицы (AB) C в силу (1.4) равен
матрицы (AB) C в силу (1.4) равен 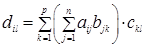 , а элемент
, а элемент 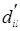 матрицы A(BC) равен
матрицы A(BC) равен 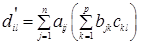 , но тогда равенство
, но тогда равенство 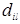 =
= 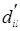 вытекает из возможности изменения порядка суммирования относительно j и k .
вытекает из возможности изменения порядка суммирования относительно j и k .
Вопрос о перестановочном свойстве произведения матрицы A на матрицу B имеет смысл ставить лишь для квадратных матриц A и B одинакового порядка (ибо, как указывалось выше, только для таких матриц A и B оба произведения AB и BA определены и являются матрицами одинаковых порядков). Элементарные примеры показывают, что произведение двух квадратных матриц одинакового порядка не обладает перестановочным свойством. В самом деле, если положить 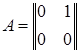 ,
, 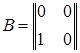 , то
, то 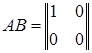 , а
, а 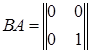 .
.
Здесь видны важные частные случаи, в которых справедливо перестановочное свойство. Две матрицы, для произведения которых справедливо перестановочное свойство, называются коммутирующими.
Среди квадратных матриц выделим класс так называемых диагональных матриц, у каждой из которых элементы, расположенные вне главной диагонали, равны нулю. Каждая диагональная матрица порядка n имеет вид
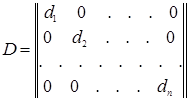 ,
,
где 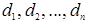 – какие угодно числа. Если все эти числа равны между собой, т.е.
– какие угодно числа. Если все эти числа равны между собой, т.е. 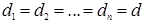 , то для любой квадратной матрицы A порядка n справедливо равенство AD=DA. Проверим это, обозначим символами
, то для любой квадратной матрицы A порядка n справедливо равенство AD=DA. Проверим это, обозначим символами 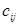 и
и 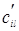 элементы, стоящие на пересечении i‑й строки и j‑го столбца матриц AD и DA соответственно. Тогда из равенства (1.4) и из вида матрицы D получим, что
элементы, стоящие на пересечении i‑й строки и j‑го столбца матриц AD и DA соответственно. Тогда из равенства (1.4) и из вида матрицы D получим, что
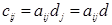 ,
, 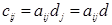 , (1.6)
, (1.6)
т.е. 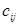 =
= 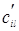 .
.
Среди всех диагональных матриц (1.5) с совпадающими элементами 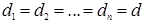 особо важную роль играют две матрицы. Первая из этих матриц получается при d=l, называется единичной матрицей n‑го порядка и обозначается символом E. Вторая матрица получается при d =0, называется нулевой матрицей n‑го порядка и обозначается символом O. Таким образом,
особо важную роль играют две матрицы. Первая из этих матриц получается при d=l, называется единичной матрицей n‑го порядка и обозначается символом E. Вторая матрица получается при d =0, называется нулевой матрицей n‑го порядка и обозначается символом O. Таким образом,
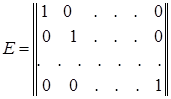 ,
, 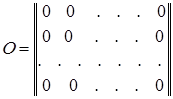 .
.
В силу доказанного выше AE = EA и AO = OA. Более того, из формул (1.6) видно, что
AE = EA = A, AO = OA = O. (1.7)
Первая из формул (1.7) характеризует особую роль единичной матрицы E, аналогичную той роли, которую играет число 1 при перемножении вещественных чисел. Что же касается особой роли нулевой матрицы O, то ее выявляет не только вторая из формул (1.7), но и элементарно проверяемое равенство
A + O = O + A = A.
Нулевой матрицей называют любую матрицу, все элементы которой равны нулю.
Блочные матрицы. Пусть некоторая матрица 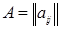 при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых представляет собой матрицу меньших размеров и называется блоком исходной матрицы. Тогда возникает возможность рассмотрения исходной матрицы A как некоторой новой (так называемой блочной) матрицы
при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых представляет собой матрицу меньших размеров и называется блоком исходной матрицы. Тогда возникает возможность рассмотрения исходной матрицы A как некоторой новой (так называемой блочной) матрицы 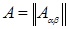 , элементами
, элементами 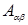 которой служат указанные блоки. Указанные элементы обозначаются большой латинской буквой, чтобы подчеркнуть, что они являются матрицами, а не числами и (как обычные числовые элементы) снабжены двумя индексами, первый из которых указывает номер «блочной» строки, а второй – номер «блочного» столбца.
которой служат указанные блоки. Указанные элементы обозначаются большой латинской буквой, чтобы подчеркнуть, что они являются матрицами, а не числами и (как обычные числовые элементы) снабжены двумя индексами, первый из которых указывает номер «блочной» строки, а второй – номер «блочного» столбца.
Например, матрицу
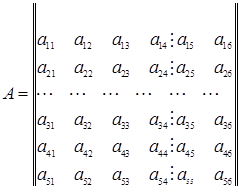
можно рассматривать как блочную матрицу
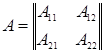 ,
,
элементами которой служат следующие блоки:
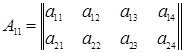 ,
, 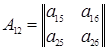 ,
,
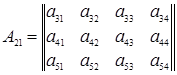 ,
, 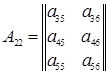 .
.
Основные операции с блочными матрицами совершаются по тем же правилам, по которым они совершаются с обычными числовыми матрицами, только в роли элементов выступают блоки.
В самом деле, элементарно проверяется, что если матрица 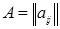 является блочной и имеет блочные элементы
является блочной и имеет блочные элементы 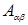 , то при том же разбиении на блоки матрице
, то при том же разбиении на блоки матрице 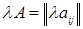 отвечают блочные элементы
отвечают блочные элементы 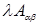 . При этом блочные элементы
. При этом блочные элементы 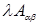 сами вычисляются по правилу умножения матрицы
сами вычисляются по правилу умножения матрицы 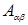 на число λ.
на число λ.
Столь же элементарно проверяется, что если матрицы A и B имеют одинаковые порядки и одинаковым образом разбиты на блоки, то сумме матриц A и B отвечает блочная матрица с элементами 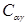 =
= 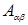 +
+ 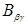 (здесь
(здесь 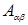 и
и 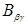 – блочные элементы матриц A и B).
– блочные элементы матриц A и B).
Пусть A и B – две блочные матрицы такие, что число столбцов каждого блока 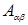 равно числу строк блока
равно числу строк блока 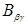 (так что при любых α, β и γ определено произведение матриц
(так что при любых α, β и γ определено произведение матриц 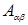
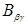 ). Тогда произведение C = AB представляет собой матрицу с элементами
). Тогда произведение C = AB представляет собой матрицу с элементами 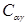 , определяемыми формулой
, определяемыми формулой
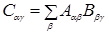 .
.
Для доказательства этой формулы достаточно расписать левую и правую ее части в терминах обычных (числовых) элементов матриц A и B.
В качестве примера применения блочных матриц остановимся на понятии так называемой прямой суммы квадратных матриц.
Определители
Целью этого параграфа является построение теории определителей любого порядка п.
Рассмотрим произвольную квадратную матрицу любого порядка n:
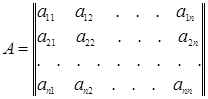 . (1.8)
. (1.8)
С каждой такой матрицей связана определенная численная характеристика, называемая определителем, соответствующим этой матрице.
Если порядок n матрицы (1.8) равен единице, то эта матрица состоит из одного элемента a 11 и определителем первого порядка соответствующим такой матрице, называется величиной этого элемента.
Если далее порядок n матрицы (1.8) равен двум, т.е. если эта матрица имеет вид
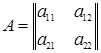 , (1.9)
, (1.9)
то определителем второго порядка, соответствующим такой матрице, есть число, равное a 11 a 22 – a 12 a 21 и обозначаемое одним из символов
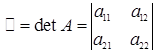 .
.
Итак, по определению
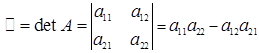 . (1.10)
. (1.10)
Формула (1.10) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.9), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и произведения элементов, стоящих на побочной ее диагонали.
Перейдем теперь к выяснению понятия определителя любого порядка n, где 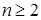 . Понятие такого определителя выводится индуктивно, считая, что понятие определителя порядка n‑1 уже введено, соответствующего произвольной квадратной матрице порядка n‑1.
. Понятие такого определителя выводится индуктивно, считая, что понятие определителя порядка n‑1 уже введено, соответствующего произвольной квадратной матрице порядка n‑1.
Договоримся называть минором любого элемента 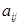 матрицы n ‑го порядка (1.8) определитель порядка n‑1, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания i ‑й строки и j ‑го столбца (той строки и того столбца, на пересечении которых стоит элемент
матрицы n ‑го порядка (1.8) определитель порядка n‑1, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания i ‑й строки и j ‑го столбца (той строки и того столбца, на пересечении которых стоит элемент 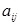 ). Минор элемента
). Минор элемента 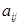 будем обозначать символом
будем обозначать символом 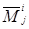 . В этом обозначении верхний индекс обозначает номер строки, нижний – номер столбца, а черта над M означает, что указанные строка и столбец вычеркиваются.
. В этом обозначении верхний индекс обозначает номер строки, нижний – номер столбца, а черта над M означает, что указанные строка и столбец вычеркиваются.
Определителем порядка n, соответствующим матрице (1.8), назовем число, равное 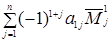 и обозначаемое символом
и обозначаемое символом
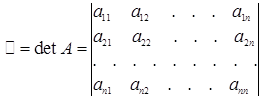 . (1.11)
. (1.11)
Итак, по определению
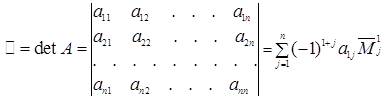 . (1.12)
. (1.12)
Формула (1.12) представляет собой правило составления определителя порядка n по элементам первой строки соответствующей ему матрицы и по минорам 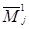 элементов первой строки, являющимся определителями порядка n‑1.
элементов первой строки, являющимся определителями порядка n‑1.
Если n =2, то правило (1.12) в точности совпадает с правилом (1.10), ибо в этом случае миноры элементов первой строки имеют вид: 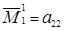 ,
, 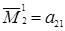 .
.
Естественно возникает вопрос, нельзя ли использовать для получения величины определителя (1.11) элементы и отвечающие им миноры не первой, а произвольной i ‑й строки матрицы (1.8). Ответ на этот вопрос дает следующая основная теорема.
Теорема 1.1. Каков бы ни был номер строки i (i =1,2… n), для определителя n ‑го порядка (1.11) справедлива формула
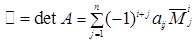 , (1.13)
, (1.13)
называемая разложением этого определителя по i ‑й строке.
В этой формуле показатель степени, в которую возводится число (–1), равен сумме номеров строки и столбца, на пересечении которых стоит элемент ai j .
Доказательство теоремы 1.1. Формулу (1.13) нужно доказать лишь для номеров i = 2, 3,…, n. При n = 2 (т.е. для определителя второго порядка) эту формулу нужно доказать лишь для номера i = 2, т.е. при n = 2 нужно доказать лишь формулу
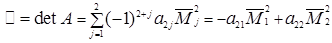
Справедливость этой последней формулы сразу вытекает из выражений для миноров матрицы (1.9) 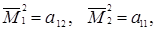 в силу которых правая часть этой формулы совпадает с правой частью (1.10). Итак, при n = 2 теорема доказана.
в силу которых правая часть этой формулы совпадает с правой частью (1.10). Итак, при n = 2 теорема доказана.
Доказательство формулы (1.13) для произвольного n > 2 производится по индукции, т.е. для определителя порядка n – 1 справедлива формула вида (1.13) разложения по любой строке, и, опираясь на это, можно убедиться в справедливости формулы (1.13) для определителя порядка n .
При доказательстве понадобится понятие миноров матрицы (1.8) порядка n – 2. Определитель порядка n‑2, соответствующий той матрице, которая получается из матрицы (1.8) в результате вычеркивания двух строк с номерами 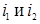 и двух столбцов с номерами
и двух столбцов с номерами 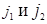 , называется минором (n‑2) – го порядка и обозначается символом
, называется минором (n‑2) – го порядка и обозначается символом 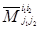 .
.
Определитель n‑го порядка ∆ вводится формулой (1.12), причем в этой формуле каждый минор 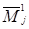 является определителем порядка n‑1, для которого по предположению справедлива формула вида (1.13) разложения по любой строке.
является определителем порядка n‑1, для которого по предположению справедлива формула вида (1.13) разложения по любой строке.
Фиксировав любой номер i (i =2,3… n), разложим в формуле (1.12) каждый минор 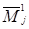 по i – й строке основного определителя (1.11) (в самом миноре
по i – й строке основного определителя (1.11) (в самом миноре 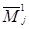 эта строка будет (i‑1) – й).
эта строка будет (i‑1) – й).
В результате весь определитель ∆ окажется представленным в виде некоторой линейной комбинации миноров (n‑2) – го порядка 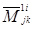 с несовпадающими номерами j и k , т.е. в виде
с несовпадающими номерами j и k , т.е. в виде
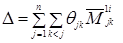 (1.14)
(1.14)
Для вычисления множителей 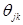 заметим, что минор
заметим, что минор 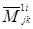 получается в результате разложения по (i‑1) – й строке только следующих двух миноров (n – 1) – го порядка, отвечающих элементам первой строки матрицы (1.8): минора
получается в результате разложения по (i‑1) – й строке только следующих двух миноров (n – 1) – го порядка, отвечающих элементам первой строки матрицы (1.8): минора 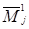 и минора
и минора 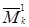 (ибо только эти два минора элементов первой строки содержат все столбцы минора
(ибо только эти два минора элементов первой строки содержат все столбцы минора 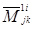 ).
).
В разложениях миноров 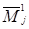 и
и 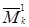 по указанной (i – 1) – й строке выписываются только слагаемые, содержащие минор
по указанной (i – 1) – й строке выписываются только слагаемые, содержащие минор 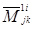 (остальные слагаемые обозначаются многоточием). Учитывая при этом, что элемент ajk минора
(остальные слагаемые обозначаются многоточием). Учитывая при этом, что элемент ajk минора 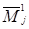 стоит на пересечении (i – 1) – й строки и (k – 1) – го столбца этого минора, а элемент aij минора
стоит на пересечении (i – 1) – й строки и (k – 1) – го столбца этого минора, а элемент aij минора 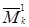 стоит на пересечении (i – 1) – й строки и j‑го столбца этого минора, в итоге получается
стоит на пересечении (i – 1) – й строки и j‑го столбца этого минора, в итоге получается
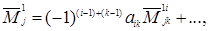 (1.15)
(1.15)
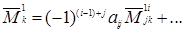 (1.16)
(1.16)
Вставляя (1.15)_ и (1.16) в правую часть (1.12) и собирая коэффициент при 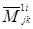 , мы получим, что множитель
, мы получим, что множитель 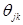 в равенстве (1.14) имеет вид
в равенстве (1.14) имеет вид
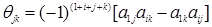 (1 17)
(1 17)
Для завершения доказательства теоремы видно, что и правая часть (1.13) равна сумме, стоящей в правой части (1.14), с теми же самыми значениями (1.17) для 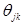 .
.
Для этого в правой части (1.13) разложим каждый минор (n‑1) – го порядка 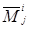 по первой строке. В результате вся правая часть (1.13) представится в виде линейной комбинации с некоторыми коэффициентами
по первой строке. В результате вся правая часть (1.13) представится в виде линейной комбинации с некоторыми коэффициентами 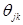 тех же самых миноров
тех же самых миноров 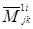
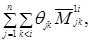 (1.18)
(1.18)
и остается вычислить множители 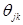 и убедиться в справедливости для них формулы (1.17).
и убедиться в справедливости для них формулы (1.17).
Для этого заметно, что минор 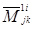 получается в результате разложения по первой строке только следующих двух миноров (n – 1) – го порядка, отвечающих элементам i‑й строки матрицы (1.8): минора
получается в результате разложения по первой строке только следующих двух миноров (n – 1) – го порядка, отвечающих элементам i‑й строки матрицы (1.8): минора 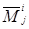 и минора
и минора 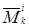 (ибо только эти два минора элементов i‑й строки содержат все столбцы минора
(ибо только эти два минора элементов i‑й строки содержат все столбцы минора 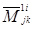 ).
).
В разложениях миноров 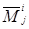 и
и 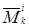 по первой строке выписывается только слагаемые, содержащие минор
по первой строке выписывается только слагаемые, содержащие минор 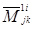 (остальные слагаемые обозначаются многоточием). Учитывая при этом, что элемент aik минора
(остальные слагаемые обозначаются многоточием). Учитывая при этом, что элемент aik минора 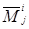 стоит на пересечении первой строки и (k‑1) – го столбца этого минора, а элемент aij минора
стоит на пересечении первой строки и (k‑1) – го столбца этого минора, а элемент aij минора 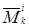 стоит на пересечении первой строки и j ‑го столбца этого минора, получается
стоит на пересечении первой строки и j ‑го столбца этого минора, получается
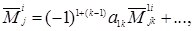 (1.19)
(1.19)
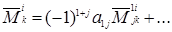 (1.20)
(1.20)
Вставляя (1.19) и (1.20) в правую часть (1.13) и собирая коэффициент при 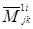 , получается, что
, получается, что 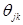 в сумме (1.18) определяется той же самой формулой (1.17), что и в равенстве (1.14).
в сумме (1.18) определяется той же самой формулой (1.17), что и в равенстве (1.14).
Теорема 1.1 доказана.
Теорема 1.1 установила возможность разложения определителя n‑го порядка по любой его строке. Естественно возникает вопрос о возможности разложения определителя n – го порядка по любому его столбцу. Положительный ответ на этот вопрос дает следующая основная теорема.
Теорема 1.2. Каков бы ни был номер столбца j (j =1,2,…, n), для определителя n ‑го порядка (1.11) справедлива формула
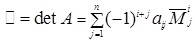 (1.21)
(1.21)
называемая разложением этого определителя по j ‑му столбцу.
Доказательство. Достаточно доказать теорему для j = 1, т.е. установить формулу разложения по первому столбцу
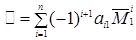 , (1.22)
, (1.22)
иначе если формула (1.22) будет установлена, то для доказательства формулы (1.21) для любого j =2,3,…, n достаточно, поменяв ролями строки и столбцы, дословно повторить схему рассуждений теоремы 1.1.
Формула (1.22) устанавливается по индукции.
При n = 2 эта формула проверяется элементарно (так как при n = 2 миноры элементов первого столбца имеют вид 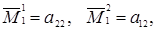 то при n = 2 правая часть (1.22) совпадает с правой частью (1.10)).
то при n = 2 правая часть (1.22) совпадает с правой частью (1.10)).
Предположим, что формула разложения по первому столбцу (1.22) верна для определителя порядка n – 1 и, опираясь на это, можно убедиться в справедливости этой формулы для определителя порядка n .
С этой целью выделим в правой части формулы (1.12) для определителя n – го порядка ∆ первое слагаемое 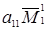 , а в каждом из остальных слагаемых разложим минор (n‑1) – го порядка
, а в каждом из остальных слагаемых разложим минор (n‑1) – го порядка 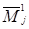 по первому столбцу.
по первому столбцу.
В результате формула (1.12) будет иметь вид
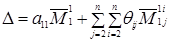 , (1.23)
, (1.23)
где 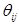 – некоторые подлежащие определению коэффициенты. Для вычисления
– некоторые подлежащие определению коэффициенты. Для вычисления 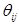 минор
минор 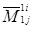 получается при разложении по первому столбцу только одного из миноров (n‑1) – го порядка, отвечающих первой строке, – минора
получается при разложении по первому столбцу только одного из миноров (n‑1) – го порядка, отвечающих первой строке, – минора 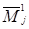 . В разложении минора
. В разложении минора 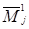 (при
(при 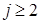 ) по первому столбцу записывается только то слагаемое, которое содержит минор
) по первому столбцу записывается только то слагаемое, которое содержит минор 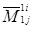 (остальные слагаемые обозначаются многоточием). Учитывая, что элемент ai1 минора
(остальные слагаемые обозначаются многоточием). Учитывая, что элемент ai1 минора 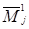 (при
(при 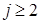 ) стоит на пересечении (i‑1) – й строки и первого столбца этого минора, получается, что при
) стоит на пересечении (i‑1) – й строки и первого столбца этого минора, получается, что при 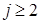
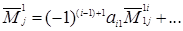 (1.24)
(1.24)
Вставляя (1.24) в правую часть (1.12) (из которой исключено первое слагаемое) и собирая коэффициент при 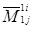 , видно,
, видно,
что коэффициент 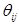 в формуле (1.23) имеет вид
в формуле (1.23) имеет вид
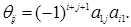 (1.25)
(1.25)
Остается доказать, что и правая часть (1.22) равна сумме, стоящей в правой части (1.23) с теми же самыми значениями (1.25) для 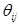 .
.
Для этого в правой части (1.22) выделяется первое слагаемое 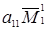 , а в каждом из остальных слагаемых раскладывается минор (n‑1) – го порядка
, а в каждом из остальных слагаемых раскладывается минор (n‑1) – го порядка 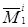 по первой строке.
по первой строке.
В результате правая часть (1.22) представится в виде суммы первого слагаемого 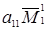 и линейной комбинацией с некоторыми коэффициентами
и линейной комбинацией с некоторыми коэффициентами 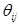 миноров (n‑2) – го порядка
миноров (n‑2) – го порядка 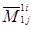 , т.е. в виде
, т.е. в виде
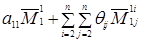 , (1.26)
, (1.26)
и остается вычислить множители 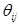 и убедиться в справедливости для них формулы (1.25).
и убедиться в справедливости для них формулы (1.25).
Для этого можно заметить, что минор 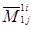 получается в результате разложения по первой строке только одного из миноров n – 1‑го порядка, отвечающих первому столбцу, – минора
получается в результате разложения по первой строке только одного из миноров n – 1‑го порядка, отвечающих первому столбцу, – минора 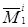 . В разложении минора
. В разложении минора 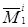 (при
(при 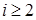 ) по первой строке записывается только то слагаемое, которое содержит минор
) по первой строке записывается только то слагаемое, которое содержит минор 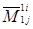 (остальные слагаемые обозначаются многоточием). Учитывая, что элемент
(остальные слагаемые обозначаются многоточием). Учитывая, что элемент 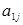 минора
минора 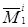 стоит на пересечении первой строки и (j‑1) – го столбца этого минора, получается, что при
стоит на пересечении первой строки и (j‑1) – го столбца этого минора, получается, что при 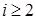
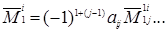 (1.27)
(1.27)
Вставляя (1.24) в правую часть (1.22), из которой исключено первое слагаемое, и собирая коэффициент при 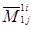 , следует, что
, следует, что 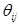 в сумме (1.26) определяется той же самой формулой (1.25), что и в равенстве (1.23). Теорема 1.2 доказана.
в сумме (1.26) определяется той же самой формулой (1.25), что и в равенстве (1.23). Теорема 1.2 доказана.
Выражение определителя непосредственно через его элементы. Установим формулу, выражающую определитель n‑го порядка непосредственно через его элементы (минуя миноры).
Пусть каждое из чисел 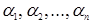 принимает одно из значений 1, 2, …, n, причем среди этих чисел нет совпадающих (в таком случае говорят, что числа
принимает одно из значений 1, 2, …, n, причем среди этих чисел нет совпадающих (в таком случае говорят, что числа 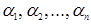 являются некоторой перестановкой чисел 1, 2, …, n). Образуем из чисел
являются некоторой перестановкой чисел 1, 2, …, n). Образуем из чисел 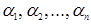 все возможные пары
все возможные пары 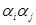 и можно говорить, что пара
и можно говорить, что пара 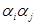 образует беспорядок, если
образует беспорядок, если 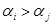 при i<j. Общее число беспорядков, образованных всеми парами, которые можно составить из чисел
при i<j. Общее число беспорядков, образованных всеми парами, которые можно составить из чисел 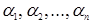 , обозначим символом
, обозначим символом 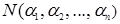 .
.
С помощью метода индукции установим для определителя n‑го порядка (1.11) следующую формулу:
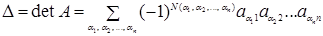 (1.28)
(1.28)
(суммирование в этой формуле идет по всем возможным перестановкам 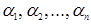 чисел 1, 2, …, n; число этих перестановок, очевидно, равно n!).
чисел 1, 2, …, n; число этих перестановок, очевидно, равно n!).
В случае n =2 формула (1.28) элементарно проверяется (в этом случае возможны только две перестановки 1, 2 и 2, 1, и, поскольку N (1, 2)=0, N (2, 1) = 1, формула (1.28) переходит в равенство (1.10)).
С целью проведения индукции предположим, что формула (1.28) при n>2 справедлива для определителя порядка (n‑1).
Тогда, записав разложение определителя п-го порядка (1.11) по первому столбцу:
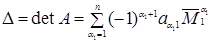 , (1.29)
, (1.29)
можно, в силу предположения индукции, представить каждый минор (n‑1) – го порядка 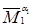 в виде
в виде
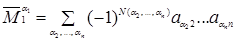 (1.30)
(1.30)
(суммирование идет по всем возможным перестановкам 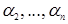 (n – 1) чисел, в качестве которых берутся все натуральные числа от 1 до n, за исключением числа
(n – 1) чисел, в качестве которых берутся все натуральные числа от 1 до n, за исключением числа 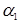 ).
).
Так как из чисел 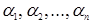 , кроме пар, образованных из чисел
, кроме пар, образованных из чисел 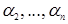 , можно образовать еще только следующие пары
, можно образовать еще только следующие пары 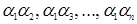 , и поскольку среди чисел
, и поскольку среди чисел 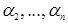 , найдется ровно (
, найдется ровно ( 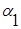 –1) чисел, меньших числа
–1) чисел, меньших числа 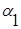 , то
, то 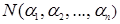 =
= 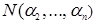 +
+ 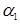 -1.
-1.
Отсюда вытекает, что 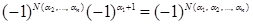 и, вставляя (1.30) в (1.29), получается формула (1.28). Тем самым вывод формулы (1.28) завершен.
и, вставляя (1.30) в (1.29), получается формула (1.28). Тем самым вывод формулы (1.28) завершен.
Теорема Лапласа. В этом пункте устанавливается формула, обобщающая формулу разложения определителя n‑го порядка по какой-либо его строке.
С этой целью вводится в рассмотрение миноры матрицы n – го порядка (1.8) двух типов.
Пусть k – любой номер, меньший n, a 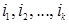 и
и 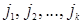 – произвольные номера, удовлетворяющие условиям
– произвольные номера, удовлетворяющие условиям 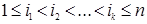 ,
, 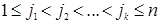 .
.
Миноры первого типа 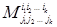 являются определителями порядка k , соответствующими той матрице, которую образуют элементы матрицы (1.8), стоящие на пересечении k строк с номерами
являются определителями порядка k , соответствующими той матрице, которую образуют элементы матрицы (1.8), стоящие на пересечении k строк с номерами 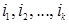 и k столбцов с номерами
и k столбцов с номерами 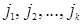 .
.
Миноры второго типа 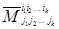 являются определителями порядка n–k , соответствующими той матрице, которая получается из матрицы (1.8) в результате вычеркивания k строк с номерами
являются определителями порядка n–k , соответствующими той матрице, которая получается из матрицы (1.8) в результате вычеркивания k строк с номерами 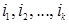 и k столбцов с номерами
и k столбцов с номерами 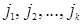 .
.
Миноры второго типа естественно назвать дополнительными по отношению к минорам первого типа.
Теорема 1.3 (теорема Лапласа). При любом номере k , меньшем n , и при любых фиксированных номерах строк 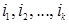 таких, что
таких, что 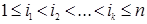 , для определителя n ‑го порядка (1.11) справедлива формула
, для определителя n ‑го порядка (1.11) справедлива формула
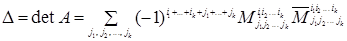 , (1.31)
, (1.31)
называемая разложением этого определителя по k строкам 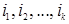 . Суммирование в этой формуле идет по всем возможным значениям индексов
. Суммирование в этой формуле идет по всем возможным значениям индексов 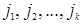 , удовлетворяющим условиям
, удовлетворяющим условиям 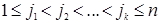 .
.
Доказательство. Прежде всего формула (1.31) является обобщением уже доказанной формулы разложения определителя n‑го порядка по одной его строке с номером i1, в которую она переходит при k = 1 (при этом минор 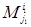 совпадает с элементом
совпадает с элементом 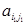 , а минор
, а минор 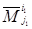 – это введенный выше минор элемента
– это введенный выше минор элемента 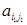 ).
).
Таким образом, при k = 1 формула (1.31) доказана. Доказательство этой формулы для любого k, удовлетворяющего неравенствам 1 < k < n, проводится по индукции, т.е. формула (1.31) справедлива для (k‑1) строк, и, опираясь на это, убедимся в справедливости формулы (1.31) для k строк.
Итак, пусть 1 < k < n и фиксированы какие угодно k строк матрицы (1.8) с номерами 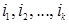 , удовлетворяющими условию
, удовлетворяющими условию 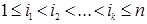 . Тогда по предположению для (k‑1) строк с номерами
. Тогда по предположению для (k‑1) строк с номерами 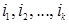 справедлива формула
справедлива формула
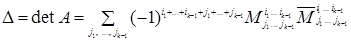 (1.32)
(1.32)
(суммирование идет по всем возможным значениям индексов 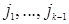 удовлетворяющим условиям
удовлетворяющим условиям 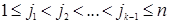 .
.
Разложим в формуле (1.32) каждый минор 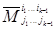 по строке, имеющей в матрице (1.8) номер ik . В результате весь определитель ∆ будет представлен в виде некоторой линейной комбинации миноров
по строке, имеющей в матрице (1.8) номер ik . В результате весь определитель ∆ будет представлен в виде некоторой линейной комбинации миноров 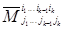 коэффициентами, которые мы обозначим через
коэффициентами, которые мы обозначим через 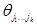 , т.е. для ∆ будет справедливо равенство
, т.е. для ∆ будет справедливо равенство
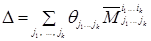 ,
,
и остается вычислить коэффициенты 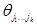 и убедиться в том, что они равны
и убедиться в том, что они равны
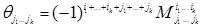 . (1.33)
. (1.33)
С этой целью заметно, что минор (n–k) – го порядка 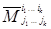 получается в результате разложения по строке с номером ik только следующих k миноров (n–k+1) – го порядка:
получается в результате разложения по строке с номером ik только следующих k миноров (n–k+1) – го порядка:
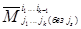 (
( 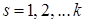 ), (1.34)
), (1.34)
ибо каждый из остальных содержащих строку is миноров (n–k+1) – го порядка не содержит всех строк и всех столбцов минора 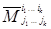 .
.
В разложении каждого минора (1.34) по строке матрицы (1.8) с номером ik выписывается только то слагаемое, которое содержит минор 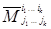 (остальные слагаемые обозначаются многоточием). Учитывая при этом, что в каждом миноре (1.34) элемент
(остальные слагаемые обозначаются многоточием). Учитывая при этом, что в каждом миноре (1.34) элемент 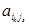 стоит на пересечении [ik – (k‑1)] – й строки и [js – (s‑1)] – го столбца этого минора, получим
стоит на пересечении [ik – (k‑1)] – й строки и [js – (s‑1)] – го столбца этого минора, получим
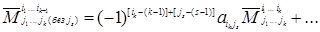
Теперь остается учесть, что в формуле (1.32) каждый минор (1.34) умножается на множитель
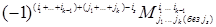
и после этого суммируется по всем s от 1 до k . Имея также в виду, что 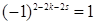 , получаем, что
, получаем, что
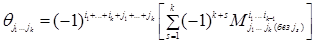 .
.
Замечая, что сумма в квадратных скобках представляет собой разложение минора 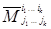 последней k‑й строке, в итоге получим для
последней k‑й строке, в итоге получим для 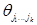 формулу (1.33). Теорема Лапласа доказана.
формулу (1.33). Теорема Лапласа доказана.
В полной аналогии с формулой (1.32) записывается и выводится формула разложения определителя по каким-либо k его столбцам.
Свойства определителей. Ниже устанавливается ряд свойств, которыми обладает произвольный определитель n‑го порядка.
Свойство равноправности строк и столбцов. Транспонированием любой матрицы или определителя называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате транспонирования матрицы A получается матрица, называемая транспонированной по отношению к матрице A и обозначаемая символом A'.
В дальнейшем мы договоримся символом |A|, |B|, |A'|… обозначать определители квадратных матриц A, B, A'… соответственно.
Первое свойство определителя формулируется так: при транспонировании величина определителя сохраняется, т.е. |А'|=|А|.
Это свойство непосредственно вытекает из теоремы 1.2 (достаточно лишь заметить, что разложение определителя |A| по первому столбцу тождественно совпадает с разложением определителя | A' | по первой строке).
Доказанное свойство означает полную равноправность строк и столбцов и позволяет нам все последующие свойства устанавливать лишь для строки быть уверенными в справедливости их и для столбцов.
Свойство антисимметрии при перестановке двух строк (или двух столбцов). При перестановке местами двух строк (или двух столбцов) определитель сохраняет свою абсолютную величину, но меняет знак на противоположный.
Для определителя второго порядка это свойство проверяется элементарно (из правила (1.10) сразу вытекает, что определители
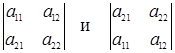
отличаются лишь знаком).
Пусть n > 2, рассмотрим теперь определитель n‑го порядка (1.11) и предположим, что в этом определителе меняются местами две строки с номерами i1 и i 2 . Записывая формулу Лапласа разложения по этим двум строкам, будет иметь
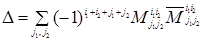 . (1.35)
. (1.35)
При перестановке местами строк с номерами i1 и i2 каждый определитель второго порядка 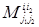 в силу доказанного выше меняет знак на противоположный, а все остальные величины, стоящие под знаком суммы в (1.35), совсем не зависят от элементов строк с номерами i1 и i 2 и сохраняют свое значение. Тем самым свойство 2° доказано.
в силу доказанного выше меняет знак на противоположный, а все остальные величины, стоящие под знаком суммы в (1.35), совсем не зависят от элементов строк с номерами i1 и i 2 и сохраняют свое значение. Тем самым свойство 2° доказано.
Линейное свойство определителя. Будем говорить, что некоторая строка ( 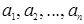 ) является линейной комбинацией строк (
) является линейной комбинацией строк ( 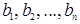 ), (
), ( 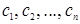 ),…, (
),…, ( 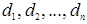 ) с коэффициентами
) с коэффициентами 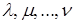 , если
, если 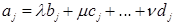 для всех j = 1, 2,…, n .
для всех j = 1, 2,…, n .
Линейное свойство определителя можно сформулировать так: если в определителе n ‑го порядка ∆ некоторая i ‑я строка ( 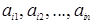 ) является линейной комбинацией двух строк (
) является линейной комбинацией двух строк ( 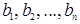 ) и (
) и ( 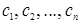 ) с коэффициентами λ и µ, то
) с коэффициентами λ и µ, то 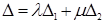 , где
, где 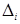 – определитель, у которого i ‑я строка равна (
– определитель, у которого i ‑я строка равна ( 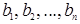 ), а все остальные строки те же, что и у ∆, а ∆2 – определитель, у которого i ‑я строка равна (
), а все остальные строки те же, что и у ∆, а ∆2 – определитель, у которого i ‑я строка равна ( 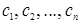 ), а все
), а все
остальные строки те же, что и у ∆.
Для доказательства разложим каждый из трех определителей 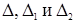 по i‑й строке и заметим, что у всех трех определителей все миноры
по i‑й строке и заметим, что у всех трех определителей все миноры 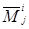 элементов i ‑й строки одинаковы. Но отсюда следует, что формула
элементов i ‑й строки одинаковы. Но отсюда следует, что формула 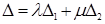 сразу вытекает из равенств
сразу вытекает из равенств 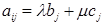 (j = 1, 2,…, n).
(j = 1, 2,…, n).
Конечно, линейное свойство справедливо и для случая, когда i‑я строка является линейной комбинацией не двух, а нескольких строк. Кроме того, линейное свойство справедливо и для столбцов определителя.
Доказанные три свойства являются основными свойствами определителя, вскрывающими его природу.
Следующие пять свойств являются логическими следствиями трех основных свойств.
Следствие 1. Определитель с двумя одинаковыми строками (или столбцами) равен нулю. В самом деле, при перестановке двух одинаковых строк, с одной стороны, определитель ∆ не изменится, а с другой стороны, в силу свойства 2° изменит знак на противоположный. Таким образом, 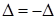 , т.е. 2∆=0 или ∆ = 0.
, т.е. 2∆=0 или ∆ = 0.
Следствие 2. Умножение всех элементов некоторой строки (или некоторого столбца) определителя на число λ равносильно умножению определителя на это число λ.
Иными словами, общий множитель всех элементов некоторой строки (или некоторого столбца) определителя можно вынести за знак этого определителя. (Это свойство вытекает из свойства 3° при μ = 0.)
Следствие 3. Если все элементы некоторой строки (или некоторого столбца) определителя равны нулю, то и сам определитель равен нулю. (Это свойство вытекает из предыдущего при λ = 0.)
Следствие 4. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю. (В самом деле, в силу следствия 2 множитель пропорциональности можно вынести за знак определителя, после чего останется определитель с двумя одинаковыми строками, который равен нулю согласно следствию 1).
Следствие 5. Если к элементам некоторой строки (или некоторого столбца) определителя прибавить соответствующие элементы другой строки (другого столбца), умноженные на произвольный множитель λ, то величина определителя не изменится. (В самом деле, полученный в результате указанного прибавления определитель можно в силу свойства 3° разбить на сумму двух определителей, первый из которых совпадает с исходным, а второй равен нулю в силу пропорциональности двух строк (или столбцов) и следствия 4.)
Следствие 5, как и линейное свойство, допускает более общую формулировку, которую приведем для строк: если к элементам некоторой строки определителя прибавить соответствующие элементы строки, являющейся линейной комбинацией нескольких других строк этого определителя (с какими угодно коэффициентами), то величина определителя не изменится.
Следствие 5 широко применяется при конкретном вычислении определителей (соответствующие примеры будут приведены в следующем пункте).
Прежде чем сформулировать еще одно свойство определителя, введем полезное понятие алгебраического дополнения данного элемента определителя.
Алгебраическим дополнением данного элемента 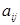 определителя n ‑го порядка (1.11) назовем число, равное
определителя n ‑го порядка (1.11) назовем число, равное 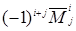 и обозначаемое символом
и обозначаемое символом 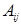 .
.
Таким образом, алгебраическое дополнение данного элемента может отличаться от минора этого элемента только знаком.
С помощью понятия алгебраического дополнения теоремы 1.1 и 1.2 можно переформулировать так: сумма произведений элементов любой строки (любого столбца) определителя на соответствующие алгебраические дополнения этой строки (этого столбца) равна этому определителю.
Соответствующие формулы разложения определителя по i‑й строке и по j‑му столбцу можно переписать так:
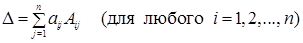 (1.13')
(1.13')
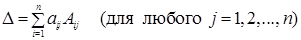 (1.21')
(1.21')
Свойство алгебраических дополнений соседних строк (или столбцов). Сумма произведений элементов какой-либо строки (или какого-либо столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (любого другого столбца) равна нулю.
Доказательство проведем для строк (для столбцов оно проводится аналогично). Записывая подробно формулу (1.13')
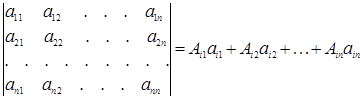 (1.36)
(1.36)
видно, что поскольку алгебраические дополнения 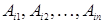 не зависят от элементов i – й строки
не зависят от элементов i – й строки 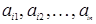 , то равенство (1.36) является тождеством относительно
, то равенство (1.36) является тождеством относительно 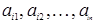 и сохраняется при замене чисел
и сохраняется при замене чисел 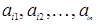 любыми другими n числами. Заменив
любыми другими n числами. Заменив 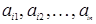 соответствующими элементами любой (отличной от i‑й) k ‑й строки
соответствующими элементами любой (отличной от i‑й) k ‑й строки 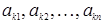 , мы получим слева в (1.36) определитель с двумя одинаковыми строками, равный нулю согласно следствию 1. Таким образом,
, мы получим слева в (1.36) определитель с двумя одинаковыми строками, равный нулю согласно следствию 1. Таким образом,
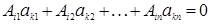
(для любых несовпадающих i и k).
Дата: 2019-05-29, просмотров: 263.