В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая (например, для вычисления средней величины стороны и квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны и кубов).
Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
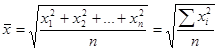 ,
,
где x1,x2,…xn- значения признака, n- их число.
Средняя квадратическая взвешенная:
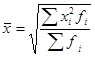 ,
,
где f-веса.
Средняя кубическая простая является кубическим корнем из частного от деления суммы кубов отдельных значений признака на их число:
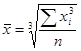 ,
,
где x1,x2,…xn- значения признака, n- их число.
Средняя кубическая взвешенная:
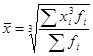 ,
,
где f-веса.
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов x, и из их отклонений от средней (х — 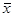 ) при расчете показателей вариации.
) при расчете показателей вариации.
Средняя может быть вычислена не для всех, а для какой-либо части единиц совокупности. Примером такой средней может быть средняя прогрессивная как одна из частных средних, вычисляемая не для всех, а только для "лучших" (например, для показателей выше или ниже сред- них индивидуальных).
Структурные средние.
Для характеристики структуры вариационных рядов применяются так называемые структурные средние. Наиболее часто используются в экономической практике мода и медиана.
Мода – значение случайной величины встречающейся с наибольшей вероятностью. В дискретном вариационном ряду это вариант имеющий наибольшую частоту.
В дискретных вариационных рядах мода определяется по наибольшей частоте. Предположим товар А реализуют в городе 9 фирм по цене в рублях:
44; 43; 44; 45; 43; 46; 42; 46;43;
Так как чаще всего встречается цена 43 рубля, то она и будет модальной.
В интервальных вариационных рядах моду определяют приближенно по формуле
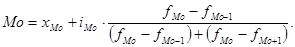 ,
,
где 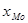 - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду;
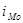 - величина модального интервала;
- величина модального интервала;
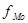 - частота модального интервала;
- частота модального интервала;
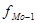 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Место нахождения модального интервала определяют по наибольшей частоте (таблица 4)
Распределение предприятий по численности промышленно - производственного персонала характеризуется следующими данными:
Таблица 4
| Группы предприятий по числу работающих, чел | Число предприятий |
| 100 — 200 | 1 |
| 200 — 300 | 3 |
| 300 — 400 | 7 |
| 400 — 500 | 30 |
| 500 — 600 | 19 |
| 600 — 700 | 15 |
| 700 — 800 | 5 |
| ИТОГО | 80 |
В этой задаче наибольшее число предприятий (30) имеет численность работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распределения.
Введем следующие обозначения:
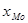 =400,
=400, 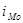 =100,
=100, 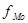 =30,
=30, 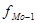 =7,
=7,  =19
=19
Подставим эти значения в формулу моды и произведем вычисления:
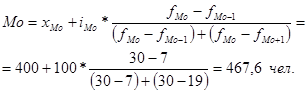
Мода применяется для решения некоторых практических задач. Так, например, при изучении товарооборота рынка берется модальная цена, для изучения спроса на обувь, одежду используют модальные размеры обуви и одежды и др.
Медиана - это численное значение признака у той единицы совокупности, которая находится в середине ранжированного ряда (построенного в порядке возрастания, либо убывания значения изучаемого признака). Медиану иногда называют серединной вариантой, т.к. она делит совокупность на две равные части.
В дискретных вариационных рядах с нечетным числом единиц совокупности - это конкретное численное значение в середине ряда. Так в группе студентов из 27 человек медианным будет рост у 14-го, если они выстроятся по росту. Если число единиц совокупности четное, то медианой будет средняя арифметическая из значений признака у двух средних членов ряда. Так, если в группе 26 человек, то медианным будет рост средний 13-го и 14-го студентов.
В интервальных вариационных рядах медиана определяется по формуле:
 , где
, где
x0 - нижняя гранича медианного интервала;
iMe - величина медианного интервала;
Sme-1 - сумма накопленных частот до медианного интервала;
fMe - частота медианного интервала.
Распределение предприятий по численности промышленно - производственного персонала характеризуется следующими данными:
Таблица 5
| Группы предприятий по числу рабочих, чел. | Число предприятий | Сумма накопительных частот |
| 100 — 200 | 1 | 1 |
| 200 — 300 | 3 | 4 (1+3) |
| 300 — 400 | 7 | 11 (4+7) |
| 400 — 500 | 30 | 41 (11+30) |
| 500 — 600 | 19 | — |
| 600 — 700 | 15 | — |
| 700 — 800 | 5 | — |
| ИТОГО | 80 |
Определим прежде всего медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений (41), соответствует интервалу 400 - 500. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле.
Известно, что:
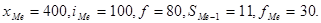
Следовательно,
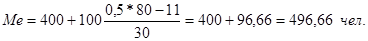 .
.
Cоотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если M0<Me< 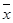 имеет место правосторонняя асимметрия. Если же
имеет место правосторонняя асимметрия. Если же 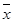 <Me<M0 - левосторонняя асимметрия ряда. По приведенному примеру можно сделать заключение, что наиболее распространенная численность рабочих является порядка 467,6 чел. В то же время более половины предприятий имеют численность рабочих более 496,6 чел., при среднем уровне 510 чел.
<Me<M0 - левосторонняя асимметрия ряда. По приведенному примеру можно сделать заключение, что наиболее распространенная численность рабочих является порядка 467,6 чел. В то же время более половины предприятий имеют численность рабочих более 496,6 чел., при среднем уровне 510 чел. 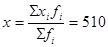 чел. Из соотношения этих показателей следует сделать вывод о правосторонней асимметрии распределения предприятий по численности промышленно - производственного персонала.
чел. Из соотношения этих показателей следует сделать вывод о правосторонней асимметрии распределения предприятий по численности промышленно - производственного персонала.
Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой-либо конкретный вариант в вариационном ряду.
Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения.
Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.
Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части — квартели, на пять равных частей — квинтели, на десять частей — децели, на сто частей — перцентели.
Расчетная часть
Задание:
1. Определите, по первичным данным таблицы №7(в методическом указании №5.2) среднегодовую стоимость основных производственных фондов в расчете на одно предприятие.
2. Постройте статистический ряд распределения предприятий по среднегодовой стоимости основных производственных фондов, образовав четыре группы предприятий с равными интервалами, охарактеризовав их числом предприятий и их удельным весом.
По ряду распределения (п.2) рассчитайте среднегодовую стоимость основных производственных фондов, взвешивая варианты признака:
а) по числу предприятий;
б) по удельному весу предприятий.
Сравните полученную среднюю с п.1, поясните их расхождение.
3. Имеются данные о финансовых показателях предприятий фирмы за отчетный период (таблица №6):
Таблица 6
| Предприятия | Получено прибыли, тыс.руб. | Акционерный капитал, тыс.руб. | Рентабельность акционерного капитала, % | Удельный вес акционерного капитала в общем объеме, % |
| A | 1 | 2 | 3 | 4 |
| 1 | 1512 | 5040 | 30 | 42 |
| 2 | 528 | 1320 | 40 | 11 |
| 3 | 1410 | 5640 | 25 | 47 |
Определите средний процент рентабельности акционерного капитала фирмы, используя показатели:
а) гр.1 и гр. 2; в) гр.1 и гр.3;
б) гр.2 и гр. 3; г) гр.3 и гр.4.
Таблица 7
| № п/п | Среднегодовая стоимость основных производственных фондов, млн. руб. | Выпуск продукции, млн. руб. |
| А | 1 | 2 |
| 1 | 27 | 21 |
| 2 | 46 | 27 |
| 3 | 33 | 41 |
| 4 | 35 | 30 |
| 5 | 41 | 47 |
| 6 | 42 | 42 |
| 7 | 53 | 34 |
| 8 | 55 | 57 |
| 9 | 60 | 46 |
| 10 | 46 | 48 |
| 11 | 39 | 45 |
| 12 | 45 | 43 |
| 13 | 57 | 48 |
| 14 | 56 | 60 |
| 15 | 36 | 35 |
| 16 | 47 | 40 |
| 17 | 20 | 24 |
| 18 | 29 | 36 |
| 19 | 26 | 19 |
| 20 | 49 | 39 |
| 21 | 38 | 35 |
| 22 | 37 | 34 |
| 23 | 56 | 61 |
| 24 | 49 | 50 |
| 25 | 37 | 38 |
| 26 | 33 | 30 |
| 27 | 55 | 51 |
| 28 | 44 | 46 |
| 29 | 41 | 38 |
| 30 | 28 | 35 |
Решение:
1. Для определения среднегодовой стоимости основных производственных фондов в расчете на одно предприятие воспользуемся формулой средней арифметической простой 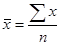 (т.к. имеются индивидуальные несгруппированные значения признака),
(т.к. имеются индивидуальные несгруппированные значения признака),
где x1,x2,…xn - среднегодовая стоимость основных производственных фондов; n – число предприятий.
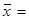
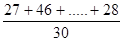 =42 (млн.руб.),
=42 (млн.руб.),
где x1=27,x2=46,…x30=28 - среднегодовая стоимость основных производственных фондов; n =30 – число предприятий.
Среднегодовая стоимость основных производственных фондов в расчете на одно предприятие равна 42 млн.руб.
2. Для построения статистического ряда распределения предприятий по среднегодовой стоимости основных производственных фондов с выделением 4 групп найдем величину равного интервала:
Величина равного интервала определяется по формуле:
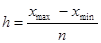 ,
,
где xmax и xmin – максимальное и минимальное значение признака, n – число групп.
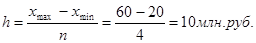
где xmax=60, xmin=20 - максимальное и минимальное значение среднегодовой стоимости основных производственных фондов (млн. руб.)
n=4 – группы предприятий.
Путем прибавления величины интервала к минимальному значению признака в группе получим следующие группы предприятий по значению среднегодовой стоимости основных производственных фондов (табл. 8)
Таблица 8
Дата: 2019-05-29, просмотров: 374.