Процедура виведення листів бінарного дерева є рекурсивною. Адже листками деякого дерева Х є листи його лівого та правого потомків (якщо ці потомки не nil). Назвемо процедуру виведення листка дерева write_tree(x:BinarTree). Якщо лівий та правий вказівники деякого елемента вказують на nil значить цей елемент є листом, а отже його треба вивести на екран. Інакше шукаємо листки лівого потомка (якщо він не рівний nil), а потім – правого потомка (якщо він також не рівний nil).
procedure write_tree(x:BinarTree);
begin
if (x^.left=nil) and (x^.right=nil) then write(x^.data,' ')
else
begin
if x^.left<>nil then write_tree(x^.left);
if x^.right<>nil then write_tree(x^.right);
end;
end;
ТЕКСТ ПРОГРАМИ ФОРМУВАННЯ БІНАРНОГО ДЕРЕВА
ТА ВИВЕДЕННЯ НА ЕКРАН ЙОГО ЛИСТІВ
uses crt;
type
BinarTree=^node;
node=record
key:integer;
data:string;
left,right,parent:BinarTree;
end;
var
b,b_parent,b_new,b_buf:BinarTree;
name:string;
k:integer;
procedure write_tree(x:BinarTree);
begin
if (x^.left=nil) and (x^.right=nil) then write(x^.data,' ')
else
begin
if x^.left<>nil then write_tree(x^.left);
if x^.right<>nil then write_tree(x^.right);
end;
end;
begin
clrscr;
repeat
write('Фамилия -> ');
readln(name);
if name<>'' then
begin
write('Ключ -> ');
readln(k);
new(b_new);
with b_new^ do
begin
parent:=nil;
left:=nil;right:=nil;
data:=name;
key:=k;
end;
if b=nil then b:=b_new
else
begin
b_buf:=b;
while b_buf<>nil do
begin
b_parent:=b_buf;
if b_new^.key<b_parent^.key then b_buf:=b_buf^.left
else b_buf:=b_buf^.right;
end;
b_new^.parent:=b_parent;
if b_new^.key<b_parent^.key then b_parent^.left:=b_new
else b_parent^.right:=b_new
end;
end;
until name='';
write('Листы дерева: ');
write_tree(b);
writeln;
end.
Результат роботи програми:
Имя -> Иванов
Ключ -> 5
Имя -> Петров
Ключ -> 3
Имя -> Сидоров
Ключ -> 8
Имя -> Ильин
Ключ -> 6
Имя ->
Листі дерева: Петров Ильин
ВИВЕДЕННЯ НА ЕКРАН УСІХ ВУЗЛІВ БІНАРНОГО ДЕРЕВА
Видозмінимо процедуру виведення листів бінарного дерева в процедуру виведення усіх його вузлів: лівий потомок - правий потомок – предок - … - кореневий вузол:
procedure write_tree(x:BinarTree);
begin
if (x^.left<>nil) or (x^.right<>nil) then
begin
if x^.left<>nil then write_tree(x^.left);
if x^.right<>nil then write_tree(x^.right);
end;
write(x^.data,' ');
end;
Тут виведення вузлів здійснюється як результат зворотньої дії рекурсивної процедури (вказівка write(x^.data,' ') – вкінці процедури). При такій організації вузли розпочнуть виводитись на екран після досягнення крайнього лівого листка.
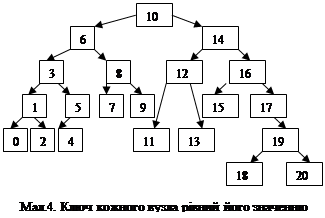
При введенні бінарного дерева, зображеного на малюнку 4, результат роботи описаної процедури буде наступним:
Все узлы дерева: 0 2 1 4 5 3 7 9 8 6 11 13 12 15 18 20 19 17 16 14 10
Якщо вказівку write(x^.data,' ') розмістити не в кінці, а на початку процедури, то виведення вузлів буде здійснюватися як результат прямої дії рекурсії. Тобто, спочатку виведуться усі ліві потомки кореня дерева, потім правий потомок предка крайнього лівого листка і всі його ліві потомки і т.д. аж до крайнього правого лиска дерева.
В цьому випадку при введенні того ж дерева (мал.4) результат роботи такої процедури наступний:
Все узлы дерева: 10 6 3 1 0 2 5 4 8 7 9 14 12 11 13 16 15 17 19 18 20
ВИЗНАЧЕННЯ КІЛЬКОСТІ РІВНІВ БІНАРНОГО ДЕРЕВА (ВИСОТИ ДЕРЕВА)
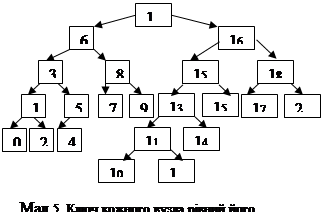
На малюнку 5 зображено шести-рівневе бінарне дерево. Лівий потомок (6) – 4-х рівневе дерево. Правий потомок (16) 5-ти рівневе дерево. Бачимо, що для того, щоб визначити висоту дерева необхідно до висоти «вищого» потомка додати 1. Виходячи з таких міркування функція визначення висоти дерева (Function height_tree(x:BinarTree):integer) має рекурсивний характер.
Нехай i – висота лівого потомка, а j – висота правого потомка. Тоді:
Function height_tree(x:BinarTree):integer;
var
i,j:integer;
begin
if x=nil then height_tree:=0
else
begin
i:=height_tree(x^.left);
j:=height_tree(x^.right);
if i>j then height_tree:=i+1
else height_tree:=j+1;
end;
end;
При введенні дерева, зображеного на мал.5, результат роботи функції height_tree наступний:
Висота дерева: 6
ВИСНОВКИ
У виконаній роботі було розглянуто процеси пошуку інформацій та розроблено структури даних для ефективного зберігання та обробки інформації. Як приклад розглянуто бінарне дерево. Це динамічна структура даних, розмір якої обмежується тільки розміром віртуальної пам’яті комп’ютера. Бінарні дерева забезпечують пошук конкретного значення, максимуму, мінімуму, попереднього, наступного, операції вставки та видалення елемента.
Розглянуті у роботі бінарні структури широко використовуються у житті, наприклад це різноманітні "ієрархічні структури", які нині широко використовуються в багатьох комп'ютерних завданнях. На даний час також розвивається граматичний аналіз, в основі якого і знаходяться принципи бінарних дерев. Граматичний аналіз на даний час широко використовується у сучасних пошукових алгоритмах.
Тому вивчення бінарних дерев та їх функціонування має важливе значення.
Дата: 2019-05-29, просмотров: 197.
