Графоаналітичний метод силового аналізу проводиться по групах Ассура.

Досліджуємо сили, що діють на групу Ассура, складену з ланок 4 та 5 (див арк. 2) і у відповідальних точках прикладаємо зовнішні сили.

У графоаналітичному методі сили інерції і момент сили інерції замінюємо однією рівнодіючою, яка за величиною дорівнює силі інерції, співпадає з нею за напрямком, а точка прикладання знаходиться на відстані hⁱ таким чином, щоб момент рівнодіючої сили відносно центра ваги співпадав за напрямком з моментом сили інерції.

Для ланки 4

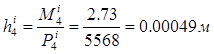
Переносимо на креслення (арк. 2) з масштабним коефіціентом μ=0,0025;  = 0,0049/0,004 = 0,123 мм

Реакції в кінематичних парах прикладаємо у вигляді двох складових, які напрямлені вздовж та перпендикулярно ланці. Для поступальної кінематичної пари направляюча – повзун, тому реакцію прикладаємо перпендикулярно направляючій.

Складаємо рівняння рівноваги для кожної ланки групи Ассура окремо

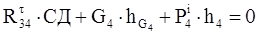
З креслення визначемо плечі сил:

СД = 0,319 м

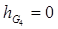
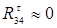
Для усієї групи Ассура складаємо векторне рівняння рівноваги:

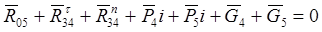
Згідно цього рівняння складаємо силовий багатокутник.Вибираємо масштабний коефіціент μ_F=77 Н/мм.

Визначаємо інші реакції ( R₀₅ та ):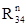

R₀₅ = 0 Н

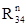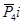
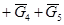= =7716,39Н

R₃₄=7716,39 H

Досліджуємо сили, що діють на группу Асура, складену з ланок 2 та 3 (див. аркуш 2) і у відповідних точках прикладаємо відповідні сили.

Сили та моменти сил інерції замінюємо рівнодіючими, які за величиною рівні силам інерції і прикладені на відстані 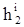 та  :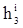

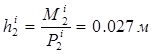
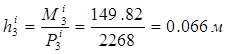
З урахуванням масштабного коефіціента μ=0,0025 знаходимо плечі рівнодійних на кресленні:

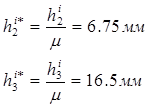
Складаємо рівняння моментів сил, що діють окремо на ланки 2 і 3 відносно точки В і визначаємо тангенціальні складові реакцій.

Для ланки 2:

,

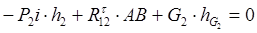де h₂ = 0,117 м,

 АВ = 0,291 м,   

.

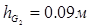І звідси :           

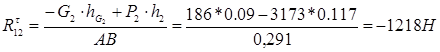
Для ланки 3:

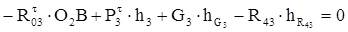
де О₂В = 0,29 м,

h₃ = 0,147 м,

     ,

.

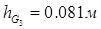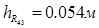І звідси :

Запишеио векторне рівняння рівноваги сил, що діють на групу Ассура, складену з ланок 2 і 3.

.

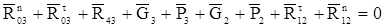Будуємо план сил відповідно до цього рівняння і визначаємо величини та напрямки реакцій  (див. арк. 2). Знайдемо довжини векторів сил на кресленні з масштабним коефіціентом μ_F=0,007Н/мм.

Визначаємо з креслення :

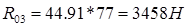
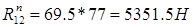
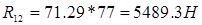
Розглянемо рух вхідної ланки. Вхідною ланкою механізму є кривошип 1, який здійснює обертальний рух. Привод у рух цієї ланки здійснюється від електродвигуна через планетарний редуктор і відкриту зубчату передачу коліс 4 і 5. Ланка 1 виконується разом з колесом 5, або жорстко з нею зв’зуються. На зубчате колесо з боку спряженого колеса 4 діє сила, яку називають зрівноважуючою, або рушійною. Накреслимо ведучу ланку разом з колесом 5 (див. аркуш 2).

Число зубів колеса 5 Z₅ = 35, колеса 4 Z₄ = 16, а модуль зубчатих колес m = 8 мм. З цих даних знайдемо радіусb колес 5 і 4:

r₅ = m × Z₅ / 2 = 140 мм.

r₄ = m × Z₄ / 2 = 64 мм.

Зрівноважуючу силу Р_зр Прикладаємо в полюсі зачеплення коліс і 5 і направимо по лінії зачепленя, яка складає з дотичною до початкових кіл кут приблизно a_w = 24°.

В точці А кривошипа прикладаємо силу реакції R₁₂ з боку ланки 2. Величину та напрямок цієї реакції визначаємо з рівності .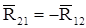

Запишемо векторне рівняння рівноваги сил, що діють на вхідну ланку:

.

Будуємо силовий трикутник відповідно векторного рівняння, з якого візначаємо сили Р_зр і R₀₁ ( масштабний коефіціент виберемо рівним μ_F=77Н/мм ). Тоді

З креслення визначаємо:

F_зр = 41,78*77=3217 Н,

R₀₁ = 63,44*77=4484,88 Н.