Несимметричный режим в трехфазной системе имеет место, если нарушается хотя бы одно из условий симметрии фазных ЭДС источника —  и равенства сопротивлений фаз приемника ZA = ZB = ZC.
и равенства сопротивлений фаз приемника ZA = ZB = ZC.
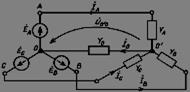
Рис. 1
При соединении фаз приемника звездой и наличии нейтрального провода (рис. 1) в общем случае несимметричного режима ток в нейтральном проводе I0 отличен от нуля и существует напряжение между нейтралями приемника и источника U0'0. В связи с этим расчет токов нельзя проводить изолированно по фазам, как в симметричном режиме.
Для расчета рассматриваемой цепи удобнее всего воспользоваться методом узловых напряжений, так как в схеме содержатся всего лишь два узла. Для единственного узлового напряжения имеем уравнение
 ,
,
из которого непосредственно находим напряжение между нейтральными точками:
 .
.
Для токов в цепи найдем далее  и аналогично для
и аналогично для 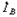 и
и 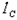 , а
, а  . Отсюда следует, что токи во всех трех фазах несимметричной системы взаимозависимы, т. е. изменение сопротивления одной из фаз ведет к изменению тока и в остальных фазах, так как при этом изменяется напряжение U0'0.
. Отсюда следует, что токи во всех трех фазах несимметричной системы взаимозависимы, т. е. изменение сопротивления одной из фаз ведет к изменению тока и в остальных фазах, так как при этом изменяется напряжение U0'0.
Полученная формула относится также и к цепи с изолированной нейтралью, для перехода к которой следует положить лишь Y0 = 0. Фазные токи в этом случае определяют по тем же формулам, что и выше.
Значения тока в несимметричной нагрузке, соединенной треугольником, при заданных фазных ЭДС можно рассчитывать с помощью преобразования треугольника ZAB, ZBC, ZCA в звезду, сопротивления фаз которой выражаются формулами:

В результате задача расчета цепи сводится к только что рассмотренной. Такое преобразование позволяет одновременно учесть и сопротивления линейных проводов ZA', ZB', ZC' , которые после преобразования оказываются включенными последовательно с фазами образовавшейся звезды ZA, ZB, ZC, изображенной на рис. 10.3 штриховыми линиями.
По этой же общей схеме рассматривают и случай, когда в несимметричной системе заданы линейные ЭДС  ,
,  и
и 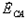 . При этом для схемы соединения звездой с изолированной нейтралью (см. рис. 10.4 при Y0 = 0) в качестве опорного узла 0' для вычисления напряжения фазы С приемника возьмем, например, вывод С генератора. В результате получим непосредственно
. При этом для схемы соединения звездой с изолированной нейтралью (см. рис. 10.4 при Y0 = 0) в качестве опорного узла 0' для вычисления напряжения фазы С приемника возьмем, например, вывод С генератора. В результате получим непосредственно

Аналогично, осуществляя круговую перестановку индексов, запишем:

Токи в фазах получим, умножая фазные напряжения 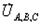 на соответствующие проводимости YA, B, C.
на соответствующие проводимости YA, B, C.
При наличии нескольких несимметричных нагрузок с различным способом соединения фаз следует воспользоваться последовательным преобразованием звезды в треугольник и обратно и эквивалентными преобразованиями параллельно или последовательно соединенных участков.
Дата: 2019-05-29, просмотров: 373.