Особенность многосторонних сопоставлений состоит не только в том, что они проводятся для группы стран, но и в том, что информация о ценах и количестве произведенной и использованной в этих странах продукции рассматривается и обрабатывается как единое целое для получения системы взаимосвязанных индексов, соответствующих ряду требований аналитического характера.

Если, например, сопоставление проводится для группы стран А, В, С, Д и Е и показатели этих стран сравниваются друг с другом на основе методологии парных сопоставлений, тогда можно получить ряд индексов Фишера для каждой пары стран: А и В, С и Д и т.д. Такие расчеты нельзя рассматривать как подлинно многосторонние сопоставления, а их результаты могут быть взаимно противоречивы. Например, в результате сопоставлений может оказаться, что A>B, B>C, C>D, а D>A. Такая возможность теоретически существует, так как в данном случае применяется метод прямых парных сопоставлений, в результате которых получаются индексы Фишера, которые, однако, нетранзитивны. Транзитивность индексов может быть обеспечена, если применяется метод многосторонних сопоставлений. Одним из таких методов многосторонних сопоставлений, который в настоящее время широко применяется на практике, является метод ЭКШ ( ЭКШ – это заглавные буквы фамилий трех статистиков, предложивших этот метод: венгров Элтетэ и Кэвеша и поляка Шульца). Формула индекса ЭКШ для стран А и В имеет следующий вид:

ЭКШ _{A/ B} ,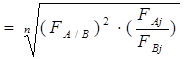

где F_{A/ B} – индекс Фишера для стран А и В;

F_Aj – индекс Фишера для стран A и J;

F_Bj – индекс Фишера для стран B и J;

n – число стран, принимающих участие в сопоставлении;

j = A, B, C,…j.

На основе формулы ЭКШ можно получить индексы, соответствующие требованию транзитивности и в наименьшей степени отступающие от требования характерности весов. В формуле ЭКШ индекс Фишера для данной пары стран (A и B) имеет вес 2. Кроме того, учитываются также индексы Фишера, полученные для данной пары стран косвенным путем, то есть через страну-посредника. Например, индекс страны A к стране B может быть получен путем деления индекса Фишера A/C на индекс Фишера B/C. Таким образом, индекс ЭКШ для стран A и B – это средний индекс из всех исчисленных прямо и косвенно индексов Фишера для стран A и B. При этом индекс Фишера, полученный на основе прямого парного сопоставления, берется весом, который равен 2. Например, если в сопоставлении принимают участие четыре страны: A, B, C и D, то индексы ЭКШ будут иметь следующий вид:

ЭКШ _A/B= ,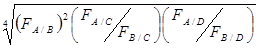

ЭКШ _A/C= ,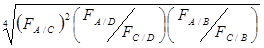

ЭКШ _A/D= ,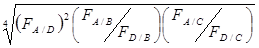

ЭКШ _C/D= ,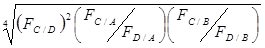

Индексы ЭКШ соответствуют требованию транзитивности и независимости от выбора страны, однако они не соответствуют требованию аддитивности, и это является их существенным недостатком.

Другим методом сопоставления, широко применяемым на практике международными организациями, является метод Гири-Камиса. Формула индекса Гири-Камиса имеет следующий вид:

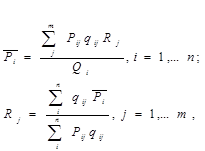
где R_j – паритет покупательной способности j-й страны по отношению к валюте базисной страны;

P_i –средняя международная цена i-го товара;

Р _ij – цена i-го товара в j-ой стране;

q _ij – количество i-го товара в j-ой стране;

Q _i – общее количество i-го товара во всех странах;

n – число товаров;

m – число стран.

Таким образом, с помощью метода Гири-Камиса можно решить систему линейных уравнений и одновременно определить ППСВ (R_j) и средние международные цены (Р_i). Оценка показателей всех стран в международных ценах позволяет получить индексы, которые транзитивны, аддитивны и не зависят от выбора базисной страны. Однако индексы Гири-Камиса не соответствуют требованию характерности весов.

Существуют и другие методы многосторонних сопоставлений. Например, в специальной литературе описан метод Уолша. Его формула имеет следующий вид:

,

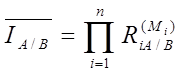где R_{iA / B} – паритет покупательной способности валют для i-ой товарной группы (исчисляется как средняя геометрическая невзвешенная из соотношений цен на товары-представители стран А и В);

М _i – доля товарной группы в общем агрегате, например в ВВП (определяется как средняя доля данной товарной группы во всех странах, принимающих участие в сопоставлении).

Индексы Уолша транзитивны, и в этом их безусловное достоинство. Они соответствуют требованию независимости индекса от выбора базисной страны, но не соответствуют требованию аддитивности.

Другой метод многосторонних международных сопоставлений – метод Джирарди – основан на использовании средних международных цен, исчисляемых исходя из средних национальных цен с помощью формулы средней геометрической невзвешенной. Индексы, получаемые на основе этого метода, соответствуют требованиям транзитивности, аддитивности и независимости от выбора базисной страны. При применении формулы Джирарди «эффект Гершенкрона» не оказывает влияния на результаты сопоставления. Однако экономическое содержание средних международных цен, исчисляемых по формуле Джирарди, неясно. Тем не менее, формула Джирарди применялась недолгое время в международных сопоставлениях ВВП на основе ППСВ, проводимых для европейских стран отделом статистики Европейского сообщества (Евростатом).

В некоторых случаях для многосторонних сопоставлений применяется метод центральной страны. В соответствии с этим методом показатели ВВП всех стран сравниваются с ВВП одной страны, рассматриваемой в качестве базисной (центральной) страны. В этом случае индексы для любой пары стран (кроме тех пар стран, одной из которых не является центральная страна) исчисляются косвенным методом, т.е. путем сопоставления индексов показателей этих стран к показателям центральной страны. Например, если в сопоставлении принимают участие четыре страны A, B, C и D, а в качестве центральной рассматривается страна A, тогда индекс, характеризующий соотношение показателей стран A и C исчисляется следующим образом:

I _{B / C} = I _{B / A} / I _{C / A .}

Индексы, получаемые таким методом, транзитивны, однако транзитивность достигается механическим путем. Это означает, что индекс I _В/С , исчисленный вышеописанным косвенным методом, будет отличаться от индекса I _В/С , исчисленного на основе прямого парного сопоставления стран B и С. Кроме того, индексы, исчисленные с помощью метода центральной страны, не соответствуют требованию независимости от выбора центральной страны. Это означает, что если бы в качестве центральной страны была избрана страна D, а не страна A, тогда соотношения между показателями всех стран были бы другими. Поэтому метод центральной страны, хотя и широко применяется на практике в международных сопоставлениях, не рассматривается как полноценный метод многосторонних сопоставлений. Его применение связано главным образом с соображениями практического характера: отсутствие исчерпывающей информации, экономия ресурсов и т.д.

Выбор метода многосторонних сопоставлений зависит от ряда факторов: целей сопоставлений, возможности получения тех или иных данных, ресурсов, которыми располагают организаторы сопоставлений, и т.д.