ВСТУП
В основу проектування операційних пристроїв різного призначення покладено принцип функціонального мікропрограмування і концепцію операційних і керуючих автоматів. При цьому мікропрограмування - це спосіб опису функцій операційних пристроїв безвідносно до технічних засобів, які використовуються для їх реалізації. Таке тлумачення мікропрограмування дозволяє формалізувати синтез структур будь-яких операційних пристроїв незалежно від способу керування роботою пристрою. Необхідно відзначити, що принципи побудови і методи проектування операційних і керуючих автоматів є тою основою, на якій базується теорія і практика проектування більшої частини пристроїв ЕОМ.
Складність і відповідальність задач, що вирішуються сучасними ЕОМ та системами, потребують від них високої надійності та продуктивності. Тому, однією з основних проблем, які стоять перед розробниками сучасної обчислювальної техніки, є підвищення продуктивності, відказостійкості та життєздатності.
В наш час основним напрямком вирішення цих проблем є створення обчислювальних машин, які побудовані з великої кількості однорідних модулів, що утворюють єдину систему шляхом встановлення логічних зв`язків між ними. В цьому суть концепції мультипроцесорних ЕОМ, частинними випадками яких є матричні, конвеєрні, з програмованою архітектурою і т.д. При цьому висовуються вимоги простоти контрольного обладнання і високої достовірності обробки інформації.
В даній курсовій роботі здійснюється розробка алгоритму операційного автомату виконання операції множення чисел в прямому коді, синтез керуючого автомату з жорсткою логікою типу Мілі. А також приведено приклад контролю виконання операції множення за допомогою 11N контролю.
РОЗРОБКА АЛГОРИТМУ ТА ОПЕРАЦІЙНОГО АВТОМАТУ
Опис операції множення
Множення може проводитись в прямому, оберненому та доповняльному кодах. Знак результату операції множення можна визначати окремо. Для цього використовується операція XOR над знаковими розрядами співмножників відповідно.
При виконанні множення двох операндів однакової розрядності розрядність результату збільшується вдвічі, порівняно з розрядністю множників. При виконанні множення операндів, представлених в прямому коді, їх модулі множаться як цілі двійкові числа без знаків, або як дробові числа без знаків, оскільки процедура множення в обох випадках та ж сама. При виконанні множення операндів, представлених в оберненому коді, всі розряди від'ємних чисел потрібно інвертувати, а далі проводити множення так само, як над даними, представленими в прямому коді. Разом з тим, потрібно зауважити, що існують методи прямого множення операндів, представлених в обернених кодах.
Основні методи множення
Методи множення чисел у двійковій системі числення можна класифікувати таким чином:
За формою подання чисел
методи множення чисел з фіксованою комою;
методи множення чисел з плаваючою комою.
За швидкодією
методи простого множення
методи прискореного множення
За видом використаного суматора:
методи множення на суматорі прямого коду;
методи множення на суматорі доповняльного коду;
методи множення на суматорі оберненого коду (рідко використовується ).
За аналізом розрядів множника:
множення з молодших розрядів;
множення зі старших розрядів;
Усі перераховані методи можуть накладатися один на одного, що дає змогу вибрати потрібний метод множення двійкових чисел з урахуванням вимог до швидкості виконання операції та до використання апаратних затрат на реалізацію алгоритму.
Виходячи з вищевикладеного можна виділити чотири варіанти схем машинного множення:
Метод 1. Припустимо В-множене (В>0), A-множник (А>0) С-добуток. Тоді у випадку зображення чисел у формі з фіксованою комою отримуємо
А = а1а2…аn ;
B = b1b2…bn = b12-1 + b22-2 + … + bn2-n;
Звідси:
С = АВ = (а1а2…аn)(b12-1 + … + bn2-n) = = (2-1,a1a2…an)b1 (1.1) + (2-1,a1a2…an)b2 + … + (2-n,a1a2…an)bn .
Множник 2-n означає зсув на n розрядів вправо числа яке заключене в дужки тобто в даному випадку зсувається вправо множене і множення починається з старших розрядів.
Структурна схема пристрою що реалізує цей метод наведена на рис. 1а.
Метод 2. Множник B = 0b1b2…bn перетворюється по схемі Горнера
B = (…((bn2-1 + bn-1)2-1 + bn-2)2-1 + … + b2)2-1 + b1)2-1
Тоді:
C = AB = (…((bn,a1a2…an)2-1 + bn-1,a1a2…an)2-1 … (1.2) …+b1,a1a2…an)2-1
Тут множення починається з молодших розрядів та зсувається вправо суми часткових добутків. Структурна схема пристрою що реалізує цей метод наведена на рис. 1б.
Метод 3. Множник записується таким чином
B = 2-n(bn + bn-121 + bn-222 + … +b12n-1).
С = AB = 2-n[bn,a1a2…an + bn-1(21,a1a2…an) + (1.3)+ bn(22,a1a2…an) + … + b1(2n-1,a1a2…an)] .
Це означає що множення починається з молодших розрядів і множене зсувається вліво на один розряд в кожному такті.
Структурна схема пристрою що реалізує цей метод наведена на рис. 1в.
Метод 4. Якщо множник записати по схемі Горнера
B = 2-n(…((b121 + b2)21 + … + bn-1)21 + bn
C = AB = 2-n(…((b1,a1a2…an)21 + b2,a1a2…an)21 + … + (1.4)+ bn-1,a1a2…an)21 + bn,a1a2…an).
У цьому випадку множення починається з старшого розряду і в кожному такті зсувається вліво сума часткових добутків.
Структурна схема пристрою що реалізує цей метод наведена на рис. 1
Другий варіант має найменші апаратурні витрати перший та третій – найменший час множення.
Таким чином для реалізації звичайної операції множення необхідно мати суматор регістри для зберігання множеного та схему аналізу розрядів множника. Суматор та регістри повинні мати ланцюги зсуву вмісту в ту чи іншу сторону у відповідності з прийнятим методом множення.
При множенні чисел на суматорі прямого коду знак добутку визначається окремо від цифрової частини як сума по модулю 2 знаків обох співмножників. У оберненому та доповняльному кодах знак добутку визначається автоматично за рахунок внесення поправок в звичайний добуток операндів.
Якщо множник від’ємний то добуток чисел на суматорі оберненого коду отримують додаванням поправок [A]об та [A]об2-n до добутку обернених кодів співмножників.[А.Я. Савельєв «Прикладная теория цифровых автоматов» М.: Высш. шк.1987]
При множенні чисел на суматорах оберненого та доповняльного кодів одночасно отримують знакову та цифрову частини.
СИНТЕЗ КЕРУЮЧОГО АВТОМАТУ
Побудова таблиці переходів
Умови переходу по мікропрограмі від одного стану до іншого задають функцію переходів автомата.
Таблиця переходів (виходів) являє собою таблицю з подвійним входом, рядки якого пронумеровані вхідними буквами, а стовпці – станами. На перетині вказується стан, у який переходить автомат (в таблиці переходів) або вихідний сигнал, що видається ним (у таблиці виходів).
Іноді при завданні автоматів Мілі використовують одну суміщену таблицю переходів і виходів, в якій на перетині стовпця аm і рядка хj записуються у вигляді аs/yg наступний стан і вихідний сигнал, що видається.
У таблиці 4 для заданого автомата маємо суміщену таблицю переходів і виходів.
Таблиця 2 – Таблиця переходів і виходів
| t | t+1 | Тригери | |||||||||
| JK2 | JK1 | JK0 | |||||||||
| ai | код ai | xi | ai+1 | код ai+1 | yi | J2 | K2 | J1 | K1 | J0 | K0 |
| a0 | 000 | 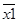
| a1 | 001 | y1,y2,y3,y4
| 0 | 0 | 0 | 0 | 1 | 0 |
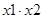
| a2 | 010 | 0 | 0 | 1 | 0 | 0 | 0 | |||

| a3 | 011 | 0 | 0 | 1 | 0 | 1 | 0 | |||
| a1 | 001 | 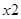
| a2 | 010 | y5 | 0 | 0 | 1 | 0 | 0 | 1 |

| a3 | 011 | 0 | 0 | 1 | 0 | 0 | 0 | |||
| a2 | 010 | ___ | a3 | 011 | y6 | 0 | 0 | 0 | 0 | 1 | 0 |
| a3 | 011 | ___ | a4 | 100 | y7,y8 | 1 | 0 | 0 | 1 | 0 | 1 |
| a4 | 100 | 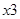
| a5 | 101 | y9,y10 | 0 | 0 | 0 | 0 | 1 | 0 |
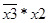
| a2 | 010 | 0 | 1 | 1 | 0 | 0 | 0 | |||
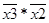
| a3 | 011 | 0 | 1 | 1 | 0 | 1 | 0 | |||
| a5 | 101 | ____ | a6 | 110 | y11 | 0 | 0 | 1 | 0 | 0 | 1 |
| a6 | 110 | ____ | a0 | 000 | y12 | 0 | 1 | 0 | 1 | 0 | 0 |
Синтез керуючого автомату
Керуючі пристрої складаються із окремих логічних схем елементів, які виробляють керуючі сигнали в заданій послідовності. Такий керуючий пристрій можна розглядати як керуючий автомат типу Мура чи Мілі.
Для автомату Мілі вихідний сигнал залежить не лише від внутрішнього стану, а й від зовнішнього стану схеми. Можна побудувати граф переходів автомата Мура, де вершинами являються стани автомата, а дугами - умови переходу з одного стану в інший.
В залежності від способу визначення вихідного сигналу в синхронних автоматах існує два способи:
вихідний сигнал y(t) однозначно визначається вхідним сигналом x(t) і станом а(t-1) автомата в слідуючий момент часу;
вихідний сигнал y(t) однозначно визначається вхідним сигналом x(t) і станом а в даний момент часу.
Автомати можна задати також у вигляді графів, таблиць виходів та переходів, суміщеної таблиці переходів і виходів. Управляючий пристрій складається із окремих логічних схем, що виробляють управляючі сигнали в заданій послідовності. Такий управляючий пристрій можна розглядати як керуючий автомат типу Мура чи Мілі.
Після побудови автомата Мілі функціонування керуючого автомата представляють у вигляді таблиць переходів і виходів. Для цього спочатку виробляють кодування станів автомата двійковими кодами, визначають тип та кількість тригерів. Потім по таблиці переходів встановлюють значення сигналів на входах тригерів, при яких відбуваються переходи; визначають функції збудження тригерів і виконують їх мінімізацію (спрощення). По знайдених виразах будується схема управляючого автомата на вибраних елементах.
В нашому випадку буде використовуватись три логічні умови Х = {х1,x2,х3} і дванадцять мікрооперацій Y = {y1, …, y10}
Отже, для кодування станів автомата необхідно 3 JK-тригера: JK0, JK1, JK2,. Закодуємо стани автомата так, як це показано у таблиці 5.
Для побудови функцій збудження тригерів і виходів використовується структурна таблиця автомата (таблиця 5).
На основі таблиці 5 будується канонічна система функцій виходів і функції збудження тригерів.
Функції виходів:
 ;
;
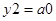 ;
;
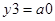 ;
;
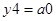 ;
;
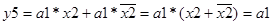 ;
;
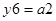 ;
;
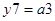 ;
;
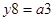 ;
;
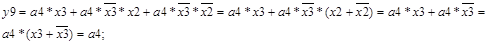
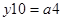 ;
;
 ;
;
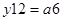 .
.
Функції збудження тригерів:
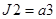 ;
;
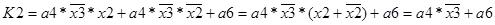 ;
;

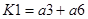 ;
;
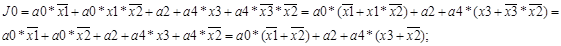
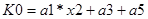 .
.
МЕТОДИКА КОНТРОЛЮ
Теоретичні відомості
Різноманітні задачі можна вирішувати за допомогою методу контролю, який оснований на властивостях порівнянь. Розвинуті на цій основі методи контролю арифметичних і логічних операцій називають контролем по модулю.
Арифметичні операції виконуються на суматорах прямого, оберненого і доповняльного коду. Допустимо, що зображення чисел зберігаються в машині деякого коду, тобто операція перетворення в заданий код на виході чи вході машини. Методика реалізації операцій контролю представляється наступним чином.
По-перше розглянемо зображення числа в відповідному коді, як єдину кодову комбінацію.
Розглянемо послідовність дій на прикладі суматора прямого коду додаються тільки цифрові частини зображення чисел, а знак зберігається, то контроль можна здійснити двома способами:
1) роздільний контроль знакової і цифрової чистин зображень результату;
2) загальний контроль всього зображення.
При роздільному способі для контролю знакових розрядів можна використовувати засіб для визначення переповнення, так як у випадку модифікованого коду поява помилок в знакових розрядах приведе до неспівпаданню інформації в них. При перевірці правильності обробки цифрових частин зображень також не виникає особах ускладнень.
При загальному способі контролю потребує корекцію контрольного коду результату із-за того, що знак результату при додаванні повторює знак доданків.
Контроль по модулю дозволяє ефективно визначити одиничні помилки. Однак одинична помилка в одному розряді може привести до ряду помилок, в декількох розрядах. Тому краще знайти засоби, які дозволять знайти не тільки одиничні помилки, але ряд їх пакетів, які можуть зустрічатись. Для цього використовуються арифметичні коди.
Одним з таких кодів є AN-код, де А-контролюєме число, N-модуль. Для таких кодів змінюються поняття відстані і ваги.
Вагою арифметичного коду прийнято вважати кількість нульових символів в кодовій комбінації, а відстань визначається як вага різниці кодових комбінацій, називають арифметичною відстанню.
А = 2і – 1 , і=2,3,…
АN1 АN2 = A(N1 N2)
Якщо ділення виконується без остачі, помилок немає, якщо з остачею – помилки є.
АN1 АN2 = A2N1 N2
АN – використовуються для контролю лише в тих пристроях, де реалізується операція ділення.
ВИСНОВКИ
В ході виконання курсової роботи проведено аналіз проблеми логiчної реалізації операції множення чисел у формі з фіксованою комою, зокрема, алгоритму множення на суматорі прямого коду, починаючи зі старших розрядів множника. Вищевказана операція перевірена на прикладі чисел А= 57 та В= - 923, а також для заданої операції побудовано алгоритм виконання множення чисел у формі з фіксованою комою. Потім за даним алгоритмом розроблено операційний та керуючий автомати. А також описана методика 11N контролю даної операції.
ПЕРЕЛІК ПОСИЛАНЬ
1. Методичні вказівки до оформлення курсових проектів (робіт) у Вінницькому національному технічному університеті / Г.Л. Лисенко, А.Г. Буда, Р.Р. Обертюх. – Вінниця: ВНТУ, 2006. – 60 с.
2. Прикладная теория цифровых автоматов: Учеб. для вузов по спец. ЭВМ / А.Я. Савельев. – М.: Высшая школа, 1987. – 272 с.
3. Прикладная теория цифровых автоматов / К.Г. Самофалов, А.М. Романкевич, В.Н. Валуйский, Ю.С Каневский, М.М. Пиневич. – К.: Вища школа. Головное изд-во, 1987. – 375 с.
4. Структура электронных вычислительных машин / С.А. Майоров, Г.И. Новиков. – Л.: Машиностроение. Ленинградское отделение, 1979. – 384 с.
5. Электронные вычислительные машины и системы: Учеб. пособие для вузов. – 3-е изд., перераб. и доп. / Б.М. Каган. – М.: Энергоатомиздат, 1991. – 592 с.
6. Цифровые ЭВМ: Теория и проектирование / К.Г. Самофалов, В.И. Корнейчук, В.П. Тарасенко. – К.: Выща школа. Головное изд-во, 1989. – 424 с.
7. Справочник по цифровой схемотехнике / В.И. Зубчук, В.П. Сигорский, А.Н. Шкуро. – К.: Тэхника, 1990. – 448 с.
ВСТУП
В основу проектування операційних пристроїв різного призначення покладено принцип функціонального мікропрограмування і концепцію операційних і керуючих автоматів. При цьому мікропрограмування - це спосіб опису функцій операційних пристроїв безвідносно до технічних засобів, які використовуються для їх реалізації. Таке тлумачення мікропрограмування дозволяє формалізувати синтез структур будь-яких операційних пристроїв незалежно від способу керування роботою пристрою. Необхідно відзначити, що принципи побудови і методи проектування операційних і керуючих автоматів є тою основою, на якій базується теорія і практика проектування більшої частини пристроїв ЕОМ.
Складність і відповідальність задач, що вирішуються сучасними ЕОМ та системами, потребують від них високої надійності та продуктивності. Тому, однією з основних проблем, які стоять перед розробниками сучасної обчислювальної техніки, є підвищення продуктивності, відказостійкості та життєздатності.
В наш час основним напрямком вирішення цих проблем є створення обчислювальних машин, які побудовані з великої кількості однорідних модулів, що утворюють єдину систему шляхом встановлення логічних зв`язків між ними. В цьому суть концепції мультипроцесорних ЕОМ, частинними випадками яких є матричні, конвеєрні, з програмованою архітектурою і т.д. При цьому висовуються вимоги простоти контрольного обладнання і високої достовірності обробки інформації.
В даній курсовій роботі здійснюється розробка алгоритму операційного автомату виконання операції множення чисел в прямому коді, синтез керуючого автомату з жорсткою логікою типу Мілі. А також приведено приклад контролю виконання операції множення за допомогою 11N контролю.
РОЗРОБКА АЛГОРИТМУ ТА ОПЕРАЦІЙНОГО АВТОМАТУ
Опис операції множення
Множення може проводитись в прямому, оберненому та доповняльному кодах. Знак результату операції множення можна визначати окремо. Для цього використовується операція XOR над знаковими розрядами співмножників відповідно.
При виконанні множення двох операндів однакової розрядності розрядність результату збільшується вдвічі, порівняно з розрядністю множників. При виконанні множення операндів, представлених в прямому коді, їх модулі множаться як цілі двійкові числа без знаків, або як дробові числа без знаків, оскільки процедура множення в обох випадках та ж сама. При виконанні множення операндів, представлених в оберненому коді, всі розряди від'ємних чисел потрібно інвертувати, а далі проводити множення так само, як над даними, представленими в прямому коді. Разом з тим, потрібно зауважити, що існують методи прямого множення операндів, представлених в обернених кодах.
Основні методи множення
Методи множення чисел у двійковій системі числення можна класифікувати таким чином:
За формою подання чисел
методи множення чисел з фіксованою комою;
методи множення чисел з плаваючою комою.
За швидкодією
методи простого множення
методи прискореного множення
За видом використаного суматора:
методи множення на суматорі прямого коду;
методи множення на суматорі доповняльного коду;
методи множення на суматорі оберненого коду (рідко використовується ).
За аналізом розрядів множника:
множення з молодших розрядів;
множення зі старших розрядів;
Усі перераховані методи можуть накладатися один на одного, що дає змогу вибрати потрібний метод множення двійкових чисел з урахуванням вимог до швидкості виконання операції та до використання апаратних затрат на реалізацію алгоритму.
Виходячи з вищевикладеного можна виділити чотири варіанти схем машинного множення:
Метод 1. Припустимо В-множене (В>0), A-множник (А>0) С-добуток. Тоді у випадку зображення чисел у формі з фіксованою комою отримуємо
А = а1а2…аn ;
B = b1b2…bn = b12-1 + b22-2 + … + bn2-n;
Звідси:
С = АВ = (а1а2…аn)(b12-1 + … + bn2-n) = = (2-1,a1a2…an)b1 (1.1) + (2-1,a1a2…an)b2 + … + (2-n,a1a2…an)bn .
Множник 2-n означає зсув на n розрядів вправо числа яке заключене в дужки тобто в даному випадку зсувається вправо множене і множення починається з старших розрядів.
Структурна схема пристрою що реалізує цей метод наведена на рис. 1а.
Метод 2. Множник B = 0b1b2…bn перетворюється по схемі Горнера
B = (…((bn2-1 + bn-1)2-1 + bn-2)2-1 + … + b2)2-1 + b1)2-1
Тоді:
C = AB = (…((bn,a1a2…an)2-1 + bn-1,a1a2…an)2-1 … (1.2) …+b1,a1a2…an)2-1
Тут множення починається з молодших розрядів та зсувається вправо суми часткових добутків. Структурна схема пристрою що реалізує цей метод наведена на рис. 1б.
Метод 3. Множник записується таким чином
B = 2-n(bn + bn-121 + bn-222 + … +b12n-1).
С = AB = 2-n[bn,a1a2…an + bn-1(21,a1a2…an) + (1.3)+ bn(22,a1a2…an) + … + b1(2n-1,a1a2…an)] .
Це означає що множення починається з молодших розрядів і множене зсувається вліво на один розряд в кожному такті.
Структурна схема пристрою що реалізує цей метод наведена на рис. 1в.
Метод 4. Якщо множник записати по схемі Горнера
B = 2-n(…((b121 + b2)21 + … + bn-1)21 + bn
C = AB = 2-n(…((b1,a1a2…an)21 + b2,a1a2…an)21 + … + (1.4)+ bn-1,a1a2…an)21 + bn,a1a2…an).
У цьому випадку множення починається з старшого розряду і в кожному такті зсувається вліво сума часткових добутків.
Структурна схема пристрою що реалізує цей метод наведена на рис. 1
Другий варіант має найменші апаратурні витрати перший та третій – найменший час множення.
Таким чином для реалізації звичайної операції множення необхідно мати суматор регістри для зберігання множеного та схему аналізу розрядів множника. Суматор та регістри повинні мати ланцюги зсуву вмісту в ту чи іншу сторону у відповідності з прийнятим методом множення.
При множенні чисел на суматорі прямого коду знак добутку визначається окремо від цифрової частини як сума по модулю 2 знаків обох співмножників. У оберненому та доповняльному кодах знак добутку визначається автоматично за рахунок внесення поправок в звичайний добуток операндів.
Якщо множник від’ємний то добуток чисел на суматорі оберненого коду отримують додаванням поправок [A]об та [A]об2-n до добутку обернених кодів співмножників.[А.Я. Савельєв «Прикладная теория цифровых автоматов» М.: Высш. шк.1987]
При множенні чисел на суматорах оберненого та доповняльного кодів одночасно отримують знакову та цифрову частини.
Дата: 2019-05-29, просмотров: 295.