Этот метод соединяет в себе достоинства метода наименьших квадратов, байесовой оценки, метода регуляризации и дает возможность решать задачу в ее некорректной постановке, обеспечивая устойчивость вычислительного процесса и позволяя получать решение, наиболее близкое к истинному режиму ЭЭС. Сущность метода обобщенной нормальной оценки состоит в следующем.
К оценке состояния ЭЭС можно подойти с позиций решения системы нелинейных алгебраических уравнений
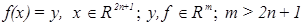(1.14)
где: m – количество измеряемых параметров режима; n+1 – общее число узлов ЭЭС.
Если известны точные значения измеряемых параметров режима у, то решение x математической модели режима (1.14) существует; оно может быть единственным или неединственным (в последнем случае нужное решение локализуется после согласования области определения и области значений) [2].
Если известны приближенные значения правых частей (1.14)
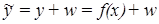(1.15)
где w – вектор случайных величин с математическим ожиданием М[w]=0, то для данной математической модели режима в пределах заданного уровня погрешности измерений существует целый класс режимов, для каждого из которых решение
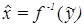(1.16)
может существовать (быть единственным или неединственным) или не существовать, а сколь угодно малые изменения измеряемых параметров могут приводить к сколь угодно большим изменениям решения [2]. По существу f отображает множество различных решений в пространстве оцениваемых параметров в неразличимое множество измерений в пространстве наблюдений.
Для некорректной модели режима требуется уточнить понятие «решение». Среди множества решений (1.15) естественно выбрать наиболее близкое к априорным данным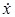 
и одновременно доставляющее измеряемым параметрам режима значения, близкие к измеренным 
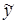. Если выбрать в качестве меры близости евклидову длину вектора, то этим требованиям отвечает решение, доставляющее минимум
, 
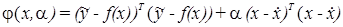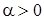. (1.17)
Первое слагаемое (аналог обобщенного решения) характеризует близость измеренных 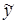и расчетных f(x) значений, второе слагаемое (аналог нормального решения) – близость априорных данных 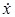и решения x. Назначение параметра регуляризации 
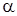– согласование меры близости в пространстве оцениваемых параметров и меры близости в пространстве наблюдений (косвенно решается проблема согласования области определения и области значений).
Решение, доставляющее минимум (1.17), называется обобщенным нормальным решением, а метод, реализующий этот критерий, – методом обобщенной нормальной оценки (МОНО).
Параметр регуляризации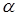 
обобщенно учитывает статистические свойства измерений и априорных данных, его значение задается априори как
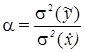
где: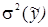 
- дисперсия измерений; 
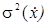- дисперсия задания априорных данных.
При таком выборе параметра регуляризации МОНО дает неухудшающуюся, устойчивую к погрешности измерений и к изменениям параметра регуляризации оценку, а верхняя норма матрицы ковариации ошибок оценки оказывается минимальной.
В качестве априорной информации, используемой при оценке состояния реальной ЭЭС, можно использовать:
1) результаты предыдущей оценки;
2) измеренные значения напряжений (их номинальные значения); ограниченность фаз узловых напряжений (d ® 0).
Второй случай менее благоприятен. Часть априорных данных (например, измеренные напряжения) принадлежит области определения, другая часть (например, фазы узловых напряжений) может и не принадлежать к ним. Достоверность таких данных различна, полученная оценка параметра регуляризации находится в широком диапазоне (10¸105) [2]. Целесообразно для каждой группы априорных данных ввести свои весовые коэффициенты:
а) CU1 – для измеренных напряжений;
б) CU2 – для номинальных напряжений (если измерений не проводилось);
в) Сd – для фаз узловых напряжений.
Тогда критерий оценки перепишется в виде
,
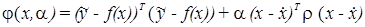где: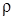 
– диагональная матрица с вышеуказанными весовыми коэффициентами, 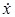– априорные данные (для фаз узловых напряжений это значения на к-ой итерации).
Для реальных ЭЭС: CU1 =10-2, CU2 =10-4, Cd =1, и диапазон изменения параметра регуляризации сужается: 103< 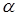<105 [2]
Численные методы решения
Принимая во внимание все выше сказанное, в конечном счете задача оценивания состояния ЭЭС сводится к решению экстремальной задачи
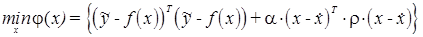(1.18)
по итерационной формуле
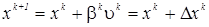, (1.19)
где: k – номер итерации;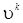 
– направление продвижения на (к+1) – ой итерации из точки хк; 
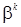– коэффициент, определяющий длину шага в направлении ; 
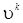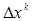– приращение на к-ой итерации; начальное приближение 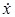задается.
В результате решения (1.19) будет получена последовательность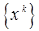 
с определенными свойствами.
Для выбранной модели режима и построенного критерия оценки эффективность алгоритма оценки состояния ЭЭС определяется свойствами численного метода решения (1.19) и характеризуется такими критериями, как: скорость и надежность сходимости, точность решения, время счета, сложность алгоритма, требуемый объем оперативной памяти ЭВМ и т.д.
Численные методы решения (1.19) используют ту или иную аппроксимацию либо целевой функции
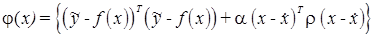(1.20)
либо вектор-функции f(x). Наибольшее распространение получил метод Ньютона-Рафсона, в котором используется разложение в ряд Тейлора нелинейной вектор-функции f(x) в окрестности произвольной точки хк до членов первого порядка малости включительно
f (x) = f (xk) + fx (xk) (x – xk). (1.21)
Подстановка (1.21) в (1.20) дает:
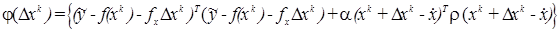
Из необходимого условия минимума следует:
,
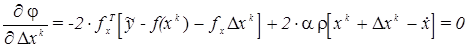тогда приращение на к-ой итерации находится
,
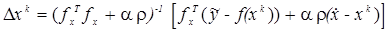где нижний индекс указывает, по какому вектор-аргументу осуществляется дифференцирование; x – x k = Dx k; x, x k – достаточно близкие точки.
Итерационный процесс (1.19) продолжается до достижения заданной точности расчетов e:
½D x k½ £ e.
Для уменьшения времени счета проверку можно производить только для модулей узловых напряжений.
Наличие стабилизирующей функции позволяет получить решение независимо от начального приближения, итерационный процесс сходится за две-четыре итерации, а число итераций в основном определяется качеством ТИ и «тяжестью» режима [2].
Оценка, вообще говоря, зависит от параметра регуляризации a. При завышенных значениях a возможно появление т.н. эффекта сглаживания, который может быть ослаблен, если воспользоваться следующим подходом.
Пусть на к-ом шаге методом Ньютона-Рафсона получена оценка хК и приращение DхК. Величина шага в направлении DхК может быть выбрана из условия достижения минимума суммы квадратов небалансов мощностей, т.е.
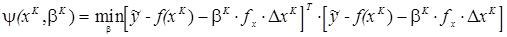
Приравняв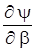 
к нулю и выразив из этого равенства 
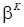, получим
.
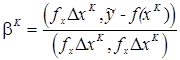Итерационный процесс, реализованный по формуле
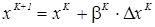, (1.22)
продолжается до тех пор, пока не будет нарушено условие
,
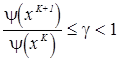где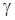 
характеризует скорость уменьшения суммы квадратов небалансов мощностей (обычно принимается равной 0.99).
Метод Ньютона-Рафсона по параметру целесообразно использовать в двух случаях:
а) когда имеются точные значения измеряемых параметров режима у;
б) когда возникают затруднения с оценкой числового значения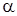 
.
Учитывая вышеперечисленные достоинства метода обобщенной нормальной оценки, естественно будет использовать его в дальнейшем для оценки состояния ЭЭС.
Вычислительные аспекты
Специфические особенности ЭЭС и МОНО играют решающую роль в рациональной организации вычислительного процесса.
Используемые при оценке состояния ЭЭС матрицы – матрица узловых проводимостей, матрица частных производных, матрица коэффициентов системы линейных алгебраических уравнений
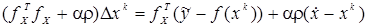(1.23)
содержат незначительное число ненулевых элементов, т.е. являются разреженными: значительного сокращения времени счета и существенной экономии используемого объема оперативной памяти ЭВМ можно добиться, если хранить ненулевые элементы и оперировать с ними.
Память, используемая для хранения разреженных матриц, состоит из двух частей: основной, содержащей числовые значения, и накладной, предназначенной для хранения информации о местоположении в матрице хранимых значений. Чем сложнее схема хранения, тем больше накладная память и меньше основная, и наоборот. Время доступа к числовым значениям и, следовательно, время счета зависит также от схемы хранения. Процесс вычислений при статичной схеме хранения, эффективный в смысле требований к памяти и времени счета, может потребовать катастрофических накладных расходов при динамичном изменении схемы хранения. Из вышесказанного следует, что схему хранения желательно выбирать с учетом процесса вычислений.
Для решения систем линейных алгебраических уравнений вида (1.23)
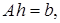
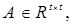
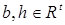(1.24)
( 
, 
)
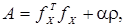
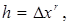
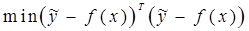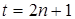используется метод Гаусса или его модификации. В методе Гаусса система уравнений (1.24) решается в два хода – прямой и обратный. При прямом ходе матрица коэффициентов приводится к верхней треугольной форме. Для этого к системе (1.24) с t неизвестными применяется (t -1) – шаговый процесс исключения неизвестных. В результате на (t -1) – ом шаге будет получена треугольная система:
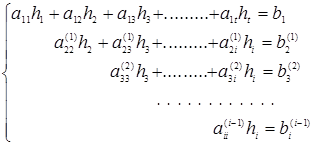(1.25)
Обратный ход метода Гаусса состоит в последовательном вычислении неизвестных из (1.25), начиная с последнего уравнения.
Рассмотренные преобразования удобно реализовать в матричном виде. Если обозначить матрицу коэффициентов (1.25)
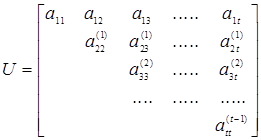(1.26)
и ввести матрицу преобразований на r – том шаге
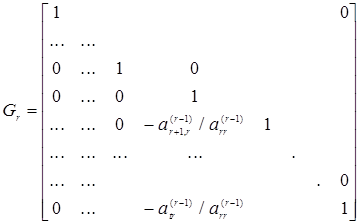(1.27)
то
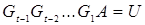. (1.28)
Операция обращения матрицы преобразования (1.27) равносильна инвертированию недиагональных элементов, а произведение нижних треугольных матриц дает такую же матрицу, поэтому
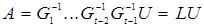(1.29)
где
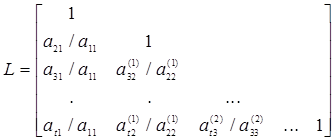(1.30)
Выражение (1.29) – т. н. LU – разложение матрицы А в виде произведения нижней треугольной матрицы L и верхней треугольной матрицы U.
Замена z=Uh показывает, что h можно получить, решая треугольные системы:
Lz=b (1.31)
Uh=z (1.32)
Выражение (1.31) – матричная запись заключительной части прямого хода метода Гаусса (пересчета свободных членов), а (1.32) – матричная запись обратного хода. Для симметричной матрицы
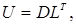
где D – диагональная матрица с элементами
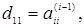i=1,2…., t,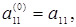 
разложение
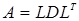(1.33)
называется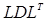 
– разложением.
Допущение относительно диагональных элементов (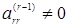 
), называемых главными, существенно. В противном случае для обеспечения численной устойчивости необходима та или иная форма выбора главного элемента, т.е. перестановки строк и (или) столбцов. Эти перестановки определяются в процессе решения системы уравнений путем компромисса между требованиями численной устойчивости и сохранением разреженности. Для разреженных матриц общего вида нельзя установить порядок исключения неизвестных, пока не начались собственно вычисления. Более того, такой выбор главного элемента может привести к крайне нежелательному росту числа ненулевых элементов.
Одно из основных достоинств МОНО состоит в том, что гауссово исключение не требует выбора главных элементов для поддержания численной устойчивости. Это означает, что матрицу коэффициентов можно переупорядочить, не заботясь о численной устойчивости, причем до начала численного решения: выбирается такая последовательность исключения неизвестных, которая приводит к появлению минимального числа ненулевых элементов. Еще одна важная особенность такого выбора исключаемой переменной состоит в симметричном переупорядочении матрицы коэффициентов – имеет место симметричная перестановка строк и столбцов [1].
Отмеченные особенности, присущие только МОНО именно в силу самого выбора параметра регуляризации, имеют далеко идущие практические последствия. Если порядок исключения неизвестных не зависит от результатов реального процесса вычислений, то наиболее трудоемкая часть расчетов, связанная с формированием структуры начального заполнения матрицы коэффициентов, ее упорядочением, резервированием места для новых ненулевых элементов, появляющихся в процессе реальных вычислений, может и должна выполняться вне реального времени на подготовительном этапе. Схема хранения должна обеспечивать высокую эффективность вычислений в реальном времени, оставаясь при этом статичной. В реальном времени реализуются вычисления, связанные с формированием и решением системы уравнений.
Т.к. матрица коэффициентов симметрична, достаточно пересчитывать и хранить только ее верхнюю треугольную часть. Если для каждой строки имеется список столбцов с ненулевыми элементами, то он полностью определяет, в каких строках элементы каких столбцов пересчитываются. Для удобства поиска в этом списке индексы столбцов желательно располагать в порядке возрастания. Например, если на r‑ом шаге в r‑ой строке ненулевые элементы находятся в столбцах r, s, q, то пересчитываются коэффициенты в s‑ой (в столбцах s и q) и в q‑ой (в столбце q) строках.
В матрице частных производных каждому i‑му узлу соответствует два столбца 2i‑1, 2i, а в матрице коэффициентов А – блочная матрица второго порядка:
.
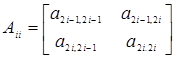Измерению ветви (i, j) соответствуют четыре ненулевые блочные матрицы: Ai i, Ai j, Aj i, Aj j (i < j). .
Для каждого такого блока местоположение всех четырех элементов однозначно определяется номером строки и номером столбца блока, что равносильно указанию места установки измерительного датчика. Аналогично, номер узла и список смежных с ним узлов определяют блоки ненулевых элементов для измерения в r‑ом узле.
Элементы матрицы коэффициентов хранятся блоками по строкам. Для каждого блока ненулевых элементов номер столбца указывается в массиве «индексы столбцов». Местоположение первого блока каждой строки задается в массиве «указатель индексов строк» [1]. Блочное представление дает существенную экономию памяти как при хранении, так и при формировании системы уравнений. В действительности кодировка расстановки ТИ непосредственно определяет местоположение блоков ненулевых элементов в схеме хранения, следовательно, отпадает необходимость запоминания промежуточных результатов (матрицы частных производных).
Т.о., все необходимые предпосылки для рациональной организации вычислительного процесса гарантируются МОНО. Наиболее трудоемкая часть расчетов должна выполняться вне реального времени на подготовительном этапе. К ним относятся:
1. Формирование структуры первоначального заполнения матрицы коэффициентов. Она (структура) однозначно определяется расстановкой ТИ и топологией электрической сети; формируется с учетом всех ТИ для типовой схемы электрических соединений, в которой все объекты, оснащенные устройствами телесигнализации (ТС), считаются включенными. Текущее состояние объектов, не оснащенных устройствами ТС, отражается в исходной схеме электрических соединений. На подготовительном этапе резервируется место для всех возможных ненулевых элементов. Сформированная таким образом структура заполнения и, следовательно, схема ее хранения может использоваться при оценивании состояния ЭЭС в реальном времени с любым составом ТИ и при любых производимых в сети коммутациях, не приводящих к появлению новых узлов: отключение части ТИ и (или) ветвей отражается только на числовых значениях элементов матрицы.
2. Упорядочение – определение последовательности исключения неизвестных. Это равносильно перенумерации узлов расчетной схемы. Предпочтительней такая последовательность исключения неизвестных, которая приводит к появлению минимального числа новых ненулевых элементов. Наиболее часто используются два алгоритма динамического упорядочения. В первом из них на каждом шаге метода Гаусса исключается неизвестная, соответствующая строка которой содержит минимальное число ненулевых элементов (если таких неизвестных несколько, то выбор произволен), во втором – неизвестная, исключение которой приводит к появлению наименьшего числа новых ненулевых элементов. Оба алгоритма дают достаточно близкие результаты, но первый алгоритм динамического упорядочения предпочтительней, так как проще, требует меньших затрат времени и памяти.
3. Имитация исключения Гаусса с резервированием места под новые ненулевые элементы и формирование схемы хранения матрицы коэффициентов. Структура первоначального заполнения (верхняя треугольная часть) запоминается блоками по строкам. С учетом установленной последовательности исключения неизвестных резервируется место для новых ненулевых элементов.
4. Формирование матрицы узловых проводимостей. Для ускорения процесса поиска нужного элемента ненулевые элементы этой матрицы, несмотря на симметричность, хранятся полностью. Схема хранения аналогична рассмотренной ранее.
В реальном времени выполняются вычисления, необходимые собственно для оценивания ЭЭС:
1. Ввод текущих ТИ.
2. Формирование системы уравнений (1.24).
3. Решение системы уравнений (1.24).
4. Реализация одного шага итерационного процесса (1.19).
5. Проверка критерия окончания счета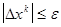 
. Если условие не выполняется, перейти к п. 2.
6. Расчет потокораспределения по результатам оценивания.
Разнесение расчетов во времени существенно упрощает алгоритм оценивания состояния ЭЭС. Возможности, заложенные на подготовительном этапе, определяют как эффективность вычислений в реальном времени в смысле экономии памяти и уменьшения времени счета, так и особенности численной реализации:
а) хранение и обработка только верхней треугольной части матрицы коэффициентов системы уравнений (1.24);
б) блочное хранение ненулевых элементов;
в) использование кодировки расстановки ТИ, непосредственно определяющей местоположение блоков ненулевых элементов;
г) вычисление в неявном виде матрицы частных производных без запоминания промежуточных результатов;
д) использование статичной схемы хранения.
Выделение подготовительного этапа, который будет называться формированием расчетной схемы, – это основная концепция построения математического обеспечения информационно-вычислительной подсистемы. Такой подход, поощряя раздельное программирование отдельных задач и их этапов, с одной стороны, максимально упрощает программы решения задач реального времени, с другой стороны, позволяет формировать расчетную схему, пригодную для решения как можно большего числа задач [2].
Дата: 2019-05-29, просмотров: 174.
