Исходными данными для проектирования редукторов с цилиндрическими зубчатыми колесами являются момент на тихоходном валу 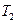 , угловые скорости быстроходного
, угловые скорости быстроходного 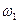 и тихоходного
и тихоходного 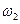 валов или значения величин, по которым можно определить
валов или значения величин, по которым можно определить  . Кроме того, задаются законы изменения нагрузки, реверсивность и срок службы (ресурс).
. Кроме того, задаются законы изменения нагрузки, реверсивность и срок службы (ресурс).
Проектирование закрытой зубчатой цилиндрической передачи со стальными колесами выполняют в такой последовательности.
1. Определяют межосевое расстояние  (мм) из условия сопротивления контактной выносливости рабочих поверхностей зубьев по формуле:
(мм) из условия сопротивления контактной выносливости рабочих поверхностей зубьев по формуле:
 , (4.9)
, (4.9)
где 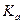 — вспомогательный коэффициент (для стальных колёс прямозубых передач
— вспомогательный коэффициент (для стальных колёс прямозубых передач 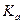 = 49,5, для косозубых и шевронных
= 49,5, для косозубых и шевронных 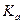 = 43);
= 43);
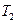 — номинальный вращающий момент на колесе в Н∙м;
— номинальный вращающий момент на колесе в Н∙м;
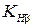 — коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии, принимают в зависимости от твердости рабочих поверхностей зубьев, расположения опор и коэффициента
— коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии, принимают в зависимости от твердости рабочих поверхностей зубьев, расположения опор и коэффициента 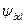 (см. рис. 4.4);
(см. рис. 4.4);
и — передаточное число;
 — коэффициент ширины венца зубчатого колеса относительно межосевого расстояния:
— коэффициент ширины венца зубчатого колеса относительно межосевого расстояния: 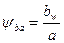 (назначают по табл. 4.8 в зависимости от твердости рабочих поверхностей и расположения колес относительно опор);
(назначают по табл. 4.8 в зависимости от твердости рабочих поверхностей и расположения колес относительно опор);
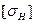 — допускаемое контактное напряжение, МПа;
— допускаемое контактное напряжение, МПа;
знак «+» ставится при расчете внешнего, «–» — внутреннего зацеплений;
103 — численный коэффициент согласования размерности.
Таблица 4.10
Рекомендуемые значения 
| Расположение зубчатых колес относительно опор (см. рис. 4.4) | Твердость зубьев | 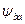
|
| Симметричное (схемы 6, 7) | Любая | 0,315; 0,4; 0,5 |
| Несимметричное (схемы 3, 4, 5) | ≤ 350 НВ ≥ 40 НRC3 | 0,315; 0,4 0,25; 0,315 |
| Консольное (схемы 1, 2) | ≤ 350 HB ≥ 40 HRC3 | 0,25 0,2 |
| Для шевронных передач | Любая | 0,4–0,63 |
| Для передач внутреннего зацепления | << | 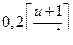
|
При выборе коэффициента 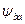 надо учитывать, что с его увеличением уменьшаются размеры и масса передачи, но вместе с тем и жесткость конструкции.
надо учитывать, что с его увеличением уменьшаются размеры и масса передачи, но вместе с тем и жесткость конструкции.
Коэффициент 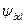 ширины венца зубчатого колеса относительно диаметра связан с коэффициентом
ширины венца зубчатого колеса относительно диаметра связан с коэффициентом 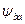 зависимостью:
зависимостью:
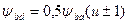 , (4.10)
, (4.10)
где знак «+» — для внешнего зацепления, «–» — для внутреннего.
Допускаемые контактные напряжения 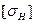 определяют по рекомендациям, приведенным в разделе 4.2. Передаточное число
определяют по рекомендациям, приведенным в разделе 4.2. Передаточное число 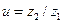 , на данной стадии расчета принимают равным передаточному отношению
, на данной стадии расчета принимают равным передаточному отношению 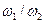 (поскольку числа зубьев еще не известны). Для цилиндрических зубчатых редукторов общего назначения номинальное передаточное число должно соответствовать одному из значений, приведенных в табл. 4.9. В курсовом проектировании допускается не согласовывать с данными таблицы.
(поскольку числа зубьев еще не известны). Для цилиндрических зубчатых редукторов общего назначения номинальное передаточное число должно соответствовать одному из значений, приведенных в табл. 4.9. В курсовом проектировании допускается не согласовывать с данными таблицы.
Таблица 4.11
Стандартные значения передаточных чисел и закрытых зубчатых передач
| 1-й ряд | 1,0 | 1,25 | 1,6 | 2,0 | 2,5 | 3,15 | 4,0 | 5,0 | 6,3 | 8,0 | 10,0 |
| 2-й ряд | - | 1,45 | 1,8 | 2,24 | 2,8 | 3,55 | 4,5 | 5,6 | 7,1 | 9,0 | - |
Примечание — 1-й ряд следует предпочитать 2-му, фактические значения, передаточных чисел  не должны отличаться от номинальных более чем на 2,5 % при и
не должны отличаться от номинальных более чем на 2,5 % при и 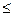 4,5 и на 4 % при и > 4,5.
4,5 и на 4 % при и > 4,5.
Полученное по формуле (4.17) значение межосевого расстояния округляют до ближайшего большего, указанного в табл. 4.12.
Таблица 4.12
Стандартные значения межосевых расстояний закрытых зубчатых передач (размеры в мм)
| 1-й ряд | 40 | 50 | 63 | 80 | 100 | 125 | 160 | 200 | 250 | 315 | 400 | 500 |
| 2-й ряд | - | - | 71 | 90 | 112 | 140 | 180 | 224 | 280 | 355 | 450 | 560 |
Примечание — 1-й ряд следует предпочитать 2-му
2. Определяют ширину венца зубчатого колеса
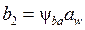 , (4.11)
, (4.11)
Для компенсации неточностей установки колес в осевом направлении ширину венца шестерни 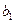 принимают на 3–5 мм больше ширины венца колеса, т.е.
принимают на 3–5 мм больше ширины венца колеса, т.е.
 , (4.11,а)
, (4.11,а)
Значения 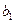 и
и 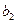 округляют до стандартных значений из нормального ряда размеров (12, 16, 20, 22, 25, 28, 32, 36, 40, 45, 50, 56, 63, 71, 80, 90, 95, 100, 105, 110, 115).
округляют до стандартных значений из нормального ряда размеров (12, 16, 20, 22, 25, 28, 32, 36, 40, 45, 50, 56, 63, 71, 80, 90, 95, 100, 105, 110, 115).
3. Определяют значение модуля передачи, используя следующие эмпирические зависимости:
mn =(0,01…0,02) aw — для улучшенных зубчатых колес (Н 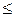 350 НB): mn =(0,0125…0,025) aw — при твердости зубьев шестерни H > 45 HRC и колеса Н
350 НB): mn =(0,0125…0,025) aw — при твердости зубьев шестерни H > 45 HRC и колеса Н 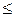 350 НB: mn =(0,016…0,0315) aw — при твердости зубьев шестерни H
350 НB: mn =(0,016…0,0315) aw — при твердости зубьев шестерни H 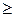 45 HRC.
45 HRC.
Мелкомодульные передачи предпочтительнее с точки зрения плавности в работе и экономии при нарезании зубьев. Однако уменьшение размера зуба приводит к понижению сопротивления изгибной усталости. Такие передачи чувствительны к концентрации нагрузки, вследствие чего необходимо повышать точность изготовления, сборки и жесткость деталей передач.
Крупномодульные передачи дольше противостоят износу, так как имеют больший размер. Они могут работать длительное время после начала выкрашивание и менее чувствительны к перегрузкам и внутренним дефектам материала.
Для обеспечения примерно равной прочности зубьев по контактной усталости активной поверхности и сопротивления усталости при изгибе модуль
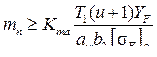 , (4.12)
, (4.12)
где 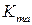 — вспомогательный коэффициент (для прямозубых колес
— вспомогательный коэффициент (для прямозубых колес 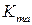 =1400, для косозубых при
=1400, для косозубых при 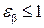
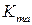 = 1100, для косозубых при
= 1100, для косозубых при  > 1 и шевронных
> 1 и шевронных 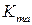 = 850. Ориентировочно значение коэффициента формы зуба YF принимаем в пределах 3,8 – 4,2. Модуль получается в миллиметрах, если в уравнение (4.12) подставляем Т1, Н∙м; a w и b2, мм;
= 850. Ориентировочно значение коэффициента формы зуба YF принимаем в пределах 3,8 – 4,2. Модуль получается в миллиметрах, если в уравнение (4.12) подставляем Т1, Н∙м; a w и b2, мм;  , МПа.
, МПа.
Полученное значение модуля 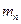 округляют до ближайшего стандартного, приведенного в табл. 4.13:
округляют до ближайшего стандартного, приведенного в табл. 4.13:
Таблица 4.13
Стандартные значения модуля для цилиндрических зубчатых передач
(размеры в мм)
| 1-й ряд 2-й ряд | 0,5 0,55 | 0,6 0,7 | 0,8 0,9 | 1,0 1,125 | 1,25 1,375 | 1,5 1,75 | 2,0 2,25 | 2,5 2,75 |
| 1-й ряд 2-й ряд | 3,0 3,5 | 4,0 4,5 | 5,0 5,5 | 6,0 7,0 | 8,0 9,0 | 10,0 11,0 | 12,0 14,0 | 16,0 18,0 |
| Примечание — 1-й ряд следует предпочитать 2-му. | ||||||||
Заметим, что для силовых передач значение модуля менее 1,5 мм применять не рекомендуется.
4. Определяют суммарное число зубьев  и угол
и угол 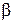 наклона зуба для косозубых и шевронных колес.
наклона зуба для косозубых и шевронных колес.
Для прямозубых передач
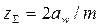 . (4.13)
. (4.13)
Число 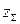 должно быть целым и обеспечивать стандартное значение межосевого расстояния
должно быть целым и обеспечивать стандартное значение межосевого расстояния 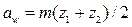 . Это условие можно соблюсти, изменяя значение модуля. Поясним это на примере.
. Это условие можно соблюсти, изменяя значение модуля. Поясним это на примере.
Для редуктора с цилиндрическими прямозубыми колесами при  = 4 из расчета на контактную прочность получено a w = 120 мм. Принимаем a w = 125 мм. При расчете модуля по формуле (4.12) получаем т = 2,68. Принимаем т = 2,75. По формуле (4.13) находим:
= 4 из расчета на контактную прочность получено a w = 120 мм. Принимаем a w = 125 мм. При расчете модуля по формуле (4.12) получаем т = 2,68. Принимаем т = 2,75. По формуле (4.13) находим:
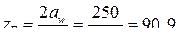 .
.
Принимаем другое стандартное значение модуля т = 2,5, тогда:
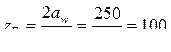 .
.
Число зубьев шестерни 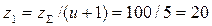 .
.
Число зубьев колеса  .
.
Проверяем значение межосевого расстояния:
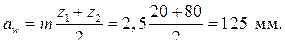
Проверяем фактическое передаточное число
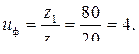
Как видно из примера, путем изменения модуля 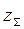 получилось целым числом,
получилось целым числом, 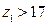 и остальные параметры передачи (
и остальные параметры передачи (  и
и 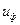 ) остались стандартными.
) остались стандартными.
Однако следует отметить, что варьирование значениями модуля ограничено и не всегда приводит к желаемым результатам. Тогда в условиях учебных проектов допускается выбирать нестандартные значения межосевого расстояния, а в условиях производства нарезают зубья со смещением.
Для косозубых и шевронных передач,
 ,
,
где 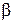 — угол наклона линии зуба. Предварительно принимают для косозубых передач
— угол наклона линии зуба. Предварительно принимают для косозубых передач 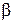 = 12° (соs 12° = 0,9781), для шевронных
= 12° (соs 12° = 0,9781), для шевронных 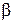 = 30° (соs 30° = 0,8660).
= 30° (соs 30° = 0,8660).
Полученное значение 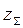 округляют в меньшую сторону до целого числа и определяют действительное значение угла
округляют в меньшую сторону до целого числа и определяют действительное значение угла 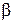 по формуле:
по формуле:
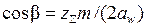 , (4.14)
, (4.14)
Точность вычислений 0,0001.
Значение угла 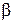 должно быть в рекомендуемом диапазоне: для косозубых передач — 8–18°, для шевронных — 25–40°.
должно быть в рекомендуемом диапазоне: для косозубых передач — 8–18°, для шевронных — 25–40°.
Заметим, что изменение угла 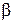 наклона линии зубьев в заданных пределах обеспечивает получение стандартного значения
наклона линии зубьев в заданных пределах обеспечивает получение стандартного значения 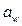 без изменения суммарного числа зубьев и модуля.
без изменения суммарного числа зубьев и модуля.
Число зубьев шестерни не должно быть менее 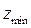 , исключающего подрезание ножки зуба
, исключающего подрезание ножки зуба
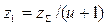 . (4.15)
. (4.15)
При нарезании зубьев без смещения для прямозубых колес 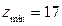 , для косозубых и шевронных колес
, для косозубых и шевронных колес
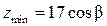 . (4.16)
. (4.16)
Число зубьев колеса
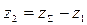 . (4.17)
. (4.17)
5. Определяют делительные диаметры колес:
· для косозубых и шевронных колес 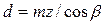 , (4.18)
, (4.18)
· для прямозубых колес  ,
,
Точность определения значений делительных диаметров не менее 0,001 мм.
Следует убедиться в том, что
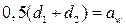
Диаметры вершин зубьев 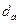 и впадин
и впадин 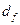 зубчатых колес передачи, выполненной без смещения, определяют по формулам:
зубчатых колес передачи, выполненной без смещения, определяют по формулам:
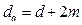 , (4.19)
, (4.19)
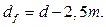 (4.20)
(4.20)
6. Вычисляют окружную скорость (м/с) в зацеплении:
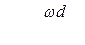 , (4.21)
, (4.21)
и назначают степень точности передачи. Для редукторов общего назначения степень точности принимают по данным таблицы 4.6.
7. Определяют силы, действующие в зацеплении (рис. 4.7):
· окружная сила 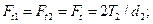
· радиальная сила 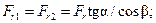 (4.22)
(4.22)
·
 |
осевая сила
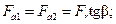
Рисунок 4.6 — Силы, действующие в зацеплении
У передач, выполненных с суммарным смещением, угол зацепления 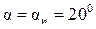 . У прямозубой передачи силы, действующие в зацеплении определяют по тем же формулам (4.22), но при этом принимают
. У прямозубой передачи силы, действующие в зацеплении определяют по тем же формулам (4.22), но при этом принимают 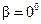 .
.
8. Выполняют проверочный расчет передачи на контактную прочность рабочих поверхностей зубьев. Определяют расчетное контактное напряжение
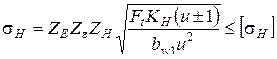 (4.23)
(4.23)
где  — коэффициент, учитывающий механические свойства материала
— коэффициент, учитывающий механические свойства материала
колес, для стальных колес  = 192;
= 192;
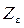 — коэффициент, учитывающий суммарную длину контактный линий, при коэффициенте осевого перекрытия
— коэффициент, учитывающий суммарную длину контактный линий, при коэффициенте осевого перекрытия 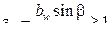 ;
; 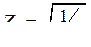 , при
, при 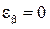 (прямозубая передача);
(прямозубая передача); 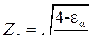 ;
;
 — коэффициент торцового перекрытия, для передач без смещения
— коэффициент торцового перекрытия, для передач без смещения
 , (4.24)
, (4.24)
В остальных случаях смотрите ГОСТ 21354–87.  — коэффициент, учитывающий форму сопряженных поверхностей зубьев;
— коэффициент, учитывающий форму сопряженных поверхностей зубьев;
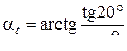 — делительный угол профиля в торцовом сечении;
— делительный угол профиля в торцовом сечении;  — основной угол наклона;
— основной угол наклона;
αtw — угол зацепления, 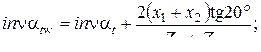
х1, х2 — коэффициент смещения исходного контура при нарезании зубьев (очевидно при);  xΣ = 0; αtw = αt = α =20°
xΣ = 0; αtw = αt = α =20°
 — окружная сила в полюсе зацепления;
— окружная сила в полюсе зацепления;
КН — коэффициент нагрузки при расчете по контактным напряжениям (см. раздел 4.3).
При проверочном расчете передачи по контактным напряжениям недогрузка или перегрузка должны составлять не более 5%.
9. Выполняем проверочный расчет передачи по напряжениям изгиба.
Расчетное напряжение из условия обеспечения выносливости зубьев колеса при изгибе:
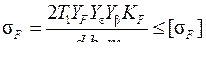 , (4.25)
, (4.25)
где 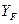 — коэффициент формы зуба, выбирают по рис. 4.7 в зависимости от приведенного числа зубьев
— коэффициент формы зуба, выбирают по рис. 4.7 в зависимости от приведенного числа зубьев 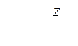 и коэффициента смещения х;
и коэффициента смещения х;
β — угол наклона линии зуба, град;
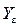 — коэффициент, учитывающий перекрытие зубьев; для прямозубых передач при предварительных расчетах
— коэффициент, учитывающий перекрытие зубьев; для прямозубых передач при предварительных расчетах 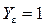 ; для косозубых при
; для косозубых при 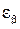 <1;
<1;  , при
, при 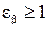 ;
; 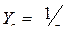 ;
;
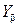 — коэффициент, учитывающий наклон зубьев,
— коэффициент, учитывающий наклон зубьев,

 — коэффициент осевого перекрытия;
— коэффициент осевого перекрытия;
 — осевой шаг;
— осевой шаг;
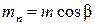 — нормальный модуль.
— нормальный модуль.
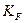 — коэффициент нагрузки при расчете по изгибу (см. раздел 4.3).
— коэффициент нагрузки при расчете по изгибу (см. раздел 4.3).
Проверка изгибной прочности выполняется отдельно для шестерни и колеса. Допускается расчет проводить по менее прочному зубу там, где меньше отношение 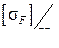 .
.
Здесь значение коэффициента  принимают по рекомендациям раздела 4.3;
принимают по рекомендациям раздела 4.3;
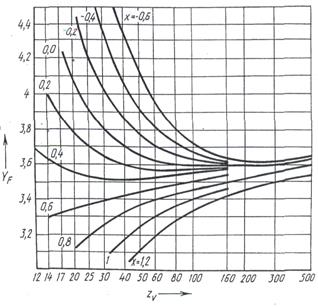
Рисунок 4.7 — График для определения коэффициента YF:
(цифры около кривых соответствуют коэффициенту смещения)
где 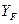 — коэффициент формы зуба, выбирают по рис. 4.5 в зависимости от числа зубьев
— коэффициент формы зуба, выбирают по рис. 4.5 в зависимости от числа зубьев 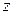 для прямозубых колес и эквивалентного числа зубьев
для прямозубых колес и эквивалентного числа зубьев  для косозубых и шевронных зубчатых колес:
для косозубых и шевронных зубчатых колес:
 .
.
Допускаемое напряжение 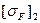 определяют по формуле (4.7).
определяют по формуле (4.7).
Для предотвращения пластических деформаций или хрупкого разрушения боковой поверхности зубьев проверяют прочность при кратковременных перегрузках. Для этого должно быть выполнено условие:
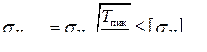 .
.
Для предотвращения хрупкого разрушения или остаточных деформаций зубьев необходимо выполнение условия 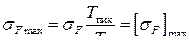 для шестерни или колеса, где Тпик — кратковременная перегрузка от внешних воздействий;
для шестерни или колеса, где Тпик — кратковременная перегрузка от внешних воздействий; 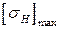 — допускаемое напряжение при проверке прочности по кратковременным перегрузкам, МПа
— допускаемое напряжение при проверке прочности по кратковременным перегрузкам, МПа 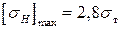 при нормализации, улучшении или объемной закалке;
при нормализации, улучшении или объемной закалке; 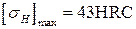 при цементации зубьев и закалке с нагревом
при цементации зубьев и закалке с нагревом 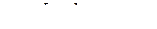 при азотированных зубьях;
при азотированных зубьях; 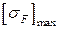 — допускаемое напряжение;
— допускаемое напряжение; 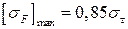 при
при 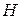 < 350 НВ;
< 350 НВ; 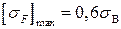 при
при 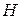 > 350 НВ.
> 350 НВ.
Дата: 2019-05-29, просмотров: 308.