Удельной поверхностью пород называется суммарная поверхность частиц или поровых каналов, содержащихся в единице объема образца. Удельная поверхность пористых тел зависит от степени дисперсности частиц, из которых они слагаются. Вследствие малых размеров отдельных зерен песка и большой плотности их укладки поверхность порового пространства пласта может достигать огромных размеров, что значительно осложняет задачу полного извлечения нефти из породы.
Величиной удельной поверхности определяются многие свойства горной породы: проницаемость, адсорбционная способность, содержание остаточной (реликтовой) воды и др. Очень важно знать удельную поверхность нефтеносных пород также в связи с большим влиянием молекулярно-поверхностных сил на процессы фильтрации нефти. Установлено, что, кроме объемных свойств жидкостей и газов, как, например, плотность, вязкость, на законы фильтрации влияют еще и молекулярные явления, происходящие на контактах жидкости и породы. Эти молекулярно-поверхностные явления могут существенным образом изменять характер фильтрации. Обычные объемные свойства жидкостей (вязкость, плотность) обусловливаются молекулами, распространенными внутри жидкой фазы, и поэтому при фильтрации жидкости через крупнозернистую породу с относительно небольшой удельной поверхностью роль молекул, находящихся на поверхности, невелика, так как их число весьма мало по сравнению с числом молекул, находящихся внутри объема жидкости. Если же пористая среда, через которую движется жидкость, имеет большую удельную поверхность, то число поверхностных молекул жидкости возрастает и становится сравнимым с числом объемных молекул. Поэтому поверхностные явления могут оказать большое влияние на процесс фильтрации жидкости.
Таким образом, удельная поверхность представляет одну из важнейших характеристик горной породы.
Следует отметить, что, несмотря на кажущуюся простоту понятия удельной поверхности, изучение и точное определение ее величины — сложная задача. Дело в том, что поры в пористой среде представлены каналами размером от десятков и сотен микрон до размеров, сравнимых с размерами молекул. Поэтому удельная поверхность глин или других адсорбентов, играющая, например, роль в процессах адсорбции, не имеет для данного пористого вещества определенной величины, а зависит от размера адсорбируемых молекул. Только для молекул с близкими размерами принципиально возможно из опытных данных получить близкие значения удельных поверхностей одного и того же адсорбента.
Для мелкопористых адсорбентов и существенно отличающихся по размерам адсорбируемых молекул наблюдаются значительные отклонения в величинах удельной поверхности (явление это носит название ультрапористости).
Чтобы представить, какова удельная поверхность естественных пород, подсчитаем общую поверхность песчинок (шаровых) радиусом r = 0,1 мм в 1 м3 песка.
Поверхность одной песчинки будет равна 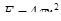 , а объем
, а объем 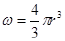
Если пористость фиктивного грунта, сложенного песчинками одинакового диаметра, равна m, то объем, занятый песчинками в единице объема породы, будет V = 1— m, а число песчинок в единице объема породы будет равно
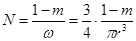
Очевидно, что суммарная поверхность всех песчинок в единице объема породы будет равна
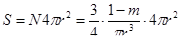 ,
,
или
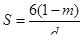 , (1.49)
, (1.49)
где d — диаметр песчинок в м; S — удельная поверхность в м2/м3; т — пористость в долях единицы.
Для песчинок радиусом г = 0,1 мм , следовательно, удельная поверхность будет равна (если пористость т = 0,26)
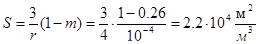
т. е. в 1 м3 песка общая поверхность частиц составит 22000 м2 .
Очевидно, что удельная поверхность глинистых пород может достигать еще большей величины и если поверхность пористой среды нефтяного пласта после окончания эксплуатации залежи останется смоченной хотя бы тончайшей пленкой нефти, это приведет к тому, что большие количества ее не будут извлечены на поверхность (табл. 6).
Таблица 6
Удельная поверхность кернов в м2/м3 некоторых нефтяных месторождений Советского Союза (по Ф.И. Котяхову и Л.И. Рубинштейну)
| № образца | Ташкала | Ромашкино | Туймазы |
| 1 | 121500 | 73000 | 38000 |
| 2 | 214000 | 85000 | 54000 |
| 3 | 330000 | 113000 | 52000 |
| 4 | 191000 | 72500 | 55000 |
| 5 | 56600 | 73000 | 90000 |
По результатам исследований Козени, Л. С. Лейбензона, К. Г. Оркина и других с удельной поверхностью связан ряд других свойств пород. Так, например, при использовании уравнения (1. 49) удельная поверхность породы по ее гранулометрическому составу может быть определена по формуле
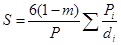 (1.50)
(1.50)
где Р — масса породы в кг; Рi — масса данной фракции в кг; di — средние диаметры фракций в м, определяемые по формуле
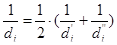 , (1.50’),
, (1.50’),
где d ’ i и д’’ i — ближайшие стандартные размеры отверстий сит.
По экспериментальным данным К. Г. Оркина при определении дельной поверхности по механическому составу в формулу (1. 50) следует ввести поправочный коэффициент, учитывающий повышение удельной поверхности вследствие нешаровидности формы зерен, величина которого равна 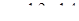 . Меньшие значения α относятся к окатанным зернам, большие — к угловатым.
. Меньшие значения α относятся к окатанным зернам, большие — к угловатым.
Используя уравнения, связывающие параметры фиктивного грунта, аналогичные формуле (1. 49), можно также установить зависимость между удельной поверхностью и другими параметрами реальных пород. Для этого при выводе соответствующих формул реальный грунт с неоднородными частицами заменяют эквивалентным естественному фиктивным грунтом, который обладает одинаковым гидравлическим сопротивлением фильтрации жидкости, с такой же удельной поверхностью, как и естественный грунт. Диаметр частиц фиктивного грунта, обладающего этими свойствами, принято называть эффективным (dэф). Сопоставляя формулы (1. 49) и (1. 50), можно видеть, что
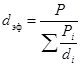 , (1.51)
, (1.51)
или
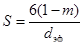 , (1.52)
, (1.52)
С другой стороны, удельную поверхность можно выразить через гидравлический радиус δ:
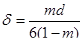 или
или 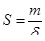 , (1.53)
, (1.53)
Гидравлический радиус, как известно, равен отношению площади порового канала к его периметру и для поры с круглым сечением, с радиусом R
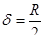
Тогда можно написать
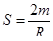 , (1.54)
, (1.54)
Подставляя значение R из формулы (1. 19), получи
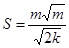 , (1.55)
, (1.55)
где k — проницаемость в м2; S — удельная поверхность в м2/м3. Если выразить проницаемость в дарси, то получим удельную поверхность в м2/м3:
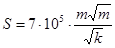 , (1.56)
, (1.56)
Из формул (1. 56) и (1. 54) следует, что чем меньше радиус поровых каналов и проницаемость породы, тем больше ее удельная поверхность.
Дата: 2019-05-29, просмотров: 469.