Итак, чтобы построить пирамиду в пропорциях золотого сечения, надо:

1. Начертить квадрат (сторона квадрата должна быть равной k*3, где k – натуральное число).

2. Построить диагонали данного квадрата.

3. В точку пересечения диагоналей опустить высоту равную стороне квадрата, делённой на 1,618.

4. Верхнюю точку высоты пирамиды соединить с четырьмя вершинами основания.

Еще информация о пирамидках из картона, фанеры…

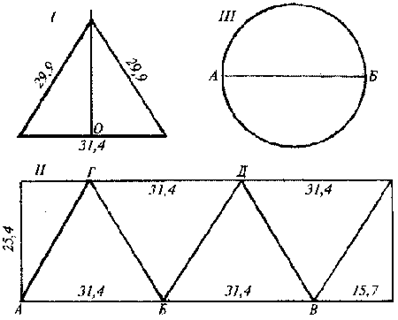
Возьмем кусок жесткого картона и прочертим на нем линию 31,4 сантиметра для основания. Из центра этого отрезка с помощью угольника проведем перпендикуляр приблизительно на 30 сантиметров вверх. Затем возьмем линейку (или циркуль), установим отметку "О" на одном из концов отрезка и приложим её так, чтобы она пересекала наш перпендикуляр на отметке "29,9". Потом прочертим от концов отрезка-основания два других отрезка к найденной точке. Вырежем полученный треугольник и повторим всю операцию четыре раза.

После этого приложим четыре треугольника друг к другу вершинами и склеим скотчем. Вот и готова ваша первая пирамида. Если вы используете другой материал (например, фанеру), то тут уже придется применить пилу и склеивать не скотчем, а настоящим клеем. И лучше даже делать фаску на краях бёдер треугольников, чтобы они точнее прилегали друг к другу при соединении.

Второй метод для изготовления картонной пирамидки высотой двадцать сантиметров состоит в следующем. Вырежьте прямоугольник со сторонами 78,5 х 25,4 сантиметра. На длинной стороне отметьте 31,4 сантиметра начиная с левого края, от полученной точки - еще раз 31,4 сантиметра. На противоположной длинной стороне начинайте с другого края. В результате у вас получатся точки А (левый край), В и С на нижней стороне и точки Д, Е и F (правый край) на верхней. Соедините их: АД, ДВ, ВЕ, ЕС и СF. Вот и получились четыре равных треугольника.

Другой пример: для пирамиды высотой тридцать сантиметров мы получаем сторону основания 30 х 1,57075 = 47,1 сантиметра, а бедро 30 х 1,4945 = 44,8 сантиметра. Обе цифры, конечно, округлённые. Если вам когда-нибудь придёт в голову соорудить коническую пирамиду (а она никогда не подводила!), то нарисуйте круг, разделите его на две половины и вырежьте оба полукружия. Затем согните оба с перехлёстом и соедините клеющей лентой. Вот и всё.

Каркас модели пирамиды.

Каркасные модели, сохраняя все свойства пирамидальной формы, позволяют не только значительно уменьшить вес конструкции, визуально наблюдать за происходящими процессами и контролировать их, но и использовать различные области её внутреннего пространства для исследовательских целей.

Сделать модель пирамиды несложно: она строится по определённым пропорциям, исходя из величины её высоты (Н), остальные необходимые показатели определяются по формулам:

Наиболее простой является каркасная модель пирамиды (см. Рис. 1), с высотой 15, 30 см и более. Эта модель может быть изготовлена из медной или алюминиевой проволоки, диаметром 2-3 мм. Более удобной является разборная модель, состоящая из тонких медных или латунных трубок, диаметр которых подбирается с учетом её высоты. В некоторых вариантах каркасной модели от вершины до основания размещается вертикальная ось (См. Рис. ).

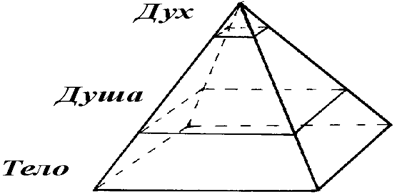
В основании пирамиды — квадрат, символизирующий собой 4 стороны света (юг, север, восток, запад); 4 основных религии (Индуизм, Буддизм, Христианство и Ислам).

А на каком уровне заканчивается Тело и начинается Душа, заканчивается Душа и начинается Дух?

Изучая материальные (физические) особенности Великой Пирамиды, ученые определили, что внутри у неё очень сильное хрономальное (временное) поле. Наибольшую силу оно имеет на 1/3 высоты пирамиды. Эта закономерность сохраняется даже на макетах пирамиды в уменьшенном размере. Сила этого поля зависит от высоты пирамиды.

Наиболее сильным потрясением для человека является отрыв его Духа и Души от Тела (смерть). Именно здесь нужно большое количество энергии, чтобы перевести человека в другое состояние. Значит, именно 1/3 пирамиды занимает Тело. Возможно, что 1/10 занимает Дух. Подтверждение этому — усечённые пирамиды и утверждение, что только 10 процентов жизни человека зависит от него самого, а на 90 процентов нами управляют законы Бога.

Если целое есть "1", то несложно вычислить арифметическую цифру Души (1/3+1/10+х=1; х=17/30). Когда арифметические цифры были переведены в математический ряд, то результаты поразили:

Тело — 1/3 = 0,3(3) — число бесконечное.

Душа — 17/30 = 0,56(6) — число бесконечное.

Дух — 1/10 = 0,10 — число постоянное.

Дух есть величина постоянная. Дух — это Любовь. Значит, Любовь к растению, животному, минералу или к человеку имеет одинаковую вибрацию. Дух — это Истина, величина постоянная, но её познание бесконечно, так как бесконечно совершенствование Души и Тела. Меняется или Тело, или Душа, и меняется отношение к Истине, но это не значит, что меняется сама Истина ("Хочешь изменить мир, измени себя самого, и мир изменится").

Делаем пирамиду, может этот вариант будет вам понятнее...

Для нашего эксперимента понадобится модель пирамиды. Её мы и постараемся сейчас изготовить.

Пирамиды могут быть разными по размерам и используемым для их строительства материалам. Все зависит от того, с какой целью вы собираетесь их применять.

Однако принципы строительства любой пирамиды одинаковы.

Предположим, что вам нужно построить четырехгранную пирамиду высотой 20 см. Для этого потребуется четыре равнобедренных треугольника, которые можно вырезать из картона.

Высота пирамиды (расстояние от вершины до центра ее основания) — это и есть исходная величина, от которой зависят все остальные параметры. Чтобы определить длину основания каждого из четырех треугольников, 20 см умножаем на число 1,57075 и получаем 31,415 см (округленно — 31,4). Для определения сторон равнобедренного треугольника те же 20 см умножаем на число 1,4945 и получаем 29,89 см (округленно — 29,9). Получился треугольник, как на рис. 1.

Изготовьте ещё три подобных треугольника. Соединять стыковые края можно с помощью клейкой ленты. Пирамида готова. Она представляет собой точную копию (в масштабе, конечно) пирамиды Хеопса.

Есть другой способ изготовления пирамиды. Он показан на следующем рис.

Вопросы: Какие пирамиды сильнее по воздействию "высокие", пропорции которых сходны с пирамидой (Голода) или "низкие", как египетские?

Пробовал сделать пирамиды сам, но выдержать точные размеры до десятых долей миллиметра невозможно, насколько сильно это влияет. Как эту проблему решали те, кто делал пирамиду сам?

Ответ: Делала пирамиду из картона, да ошибки есть …, но ОНА работает даже с ошибками! Видимо тут идёт влияние самой фигуры, и соблюдение пропорций, а не доли миллиметров.

При изготовлении пирамиды производятся довольно сложные вычисления. Есть ли метод проще?

Правильная пирамида - это разновидность пирамид, у которой в основании лежит правильный четырёхугольник - квадрат. Боковые же грани пирамиды представляют из себя равнобедренные треугольники. Исходя из этих данных, правильную пирамиду довольно легко построить. Смотрим!

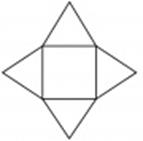
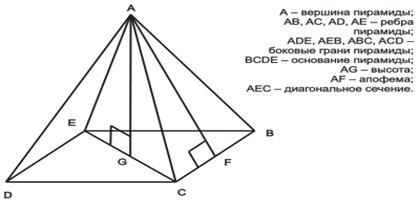
Рис.1                                                         Рис.2

Сначала берётся лист бумаги, а затем на нём рисуется квадрат примерно, таким образом, как это показано выше.

Затем нужно начертить 4 равнобедренных треугольника так, чтобы стороны квадрата стали основаниями этих треугольников. Нельзя забывать, что равносторонний треугольник является разновидностью равнобедренного.

Это принципиально лишь в том случае, если нужно сделать высокую/невысокую пирамиду. Основание же треугольников останется неизменным. Теперь берутся ножницы, и вырезается получившееся подобие четырехконечной звезды. Потом "лучи" этй "звезды" сгибаются в одну сторону, где будет вершина пирамиды. Если всё сделано, верно, то из треугольников выйдут грани пирамиды, кончики "лучей" соединятся в одном месте и образуют вершину пирамиды. Затем грани скрепляются и получается то, что изображено на первом рисунке.

По утверждениям некоторых эзотериков, различные свойства пирамидам придают не рёбра, а грани, т.е. важно, чтобы был соблюдён угол наклона граней, а их количество значения не имеет. В пределе, это может быть конус, который не требуется ориентировать в пространстве. Изготовление 8-ми, 12-гранных пирамид позволяет лучше использовать пространство внутри пирамиды (например, в качестве теплицы), и снижает требования к ориентации в пространстве.

Более практично строить так называемые пирамиды "Жизни". Это тоже одна из пирамид живого сечения, последовательность радиусов соответствует 1, 1/ F^2, 1/ F^4, 1/ F^6+. Отношение Н/L = 1. Они более устойчивы к ветровым нагрузкам, чем пирамиды "Голода", и в то же время, угол наклона граней 63.5 градуса более комфортен.

Вот пример расчета:

Высота ............Основание .......Ребро

1,5 ...................... 2,35 ..................... 2,24

2.0 ...................... 3,14 .................... 2,99

2,3 ....................... 3,61 ..................... 3,44

2,5 ....................... 3,92 ...................... 3,74

3,0 ....................... 4,71 ...................... 4,48

3,5 ........................ 5,49 ..................... 5,23

Следует помнить, что максимальными энергетическими возможностями всех правильно изготовленных и установленных пирамид (больших и малых) обладает их внутреннее пространство на уровне от 1/3 до 2/3 высоты пирамиды. Все остальное пространство пирамид энергетически минимально, соответственно, и отдача минимальна.

1. Пирамида Александра Голода. Одна из них стоит в районе Волго-верховья, другая на 38 км по шоссе Москва-Рига.

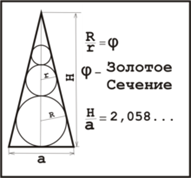
2. Пирамида Хеопса.

Бывают и готовые чертежи-варианты для изготовления пирамиды в различных журналах, на сайтах и т.д., просто распечатать, вырезать, склеить и всё, не заморачиваться!

Может этот вариант объяснения будет кому-то более подходящим? Как сделать пирамиду из картона?

Пирамида является символьным предметом. Издревле считалось, что она способна гармонизировать окружающий мир человека, которому она подарена, а также представляет собой наиболее правильную форму бытия. Недаром египетские пирамиды сохранились до сих пор в неизменном виде.