На местности обозначены точки А и В. Найдите точки C, D и E, для которых выполнены равенства 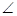 BAC=45°, 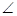BAD=6O,° 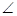BAE =3O°.

Решение: проложим перпендикуляр к прямой АВ (задача 4), пересекающий в какой–то точке луч АВ (задача 3). Будем считать для удобства, что эта точка пересечения и есть точка В. На перпендикуляре по разные стороны от точки В отложить точки С и F (задача 2), удалённые от точки В на расстояние АВ (задача 5). Тогда угол ВАС равен 45° (из равнобедренного  прямоугольного треугольника АВС). На прямой AF отложим точку G на расстоянии АВ от точки А, а затем на прямой ВС отложим точку D на расстоянии CG от точки В. Тогда угол ВА D равен 6О°, так как по теореме Пифагора для прямоугольного треугольников АВС, ACG и ABD имеют место равенства

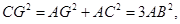
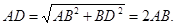
Для построения точки Е теперь остаётся проложить биссектрису угла BAD .

Задача 11. Построение треугольника по двум сторонам и высоте к третьей стороне

Постройте треугольник по двум сторонам и высоте к третьей стороне.

Даны три отрезка M₁N₁, M₂N₂, M₃N₃. Требуется построить такой треугольник АВС, у которого две стороны АВ и АС равны соответственно данным отрезкам M₁N₁ и M₂N₂, а высота АН равна отрезку M₃N₃.

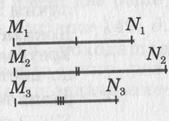
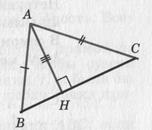
Решение: построим прямоугольный треугольник АВН, у которого гипотенуза равна отрезку M₁N₁, а катет АН равен данному отрезку M₃N₃.

Затем проводим окружность радиуса M₂N₂ с центром в точке А. Одну из точек пересечения этой окружности с прямой ВН обозначим буквой С. Проведя отрезки ВС и АС, получим искомый треугольник АВС.

Заключение

В настоящей работе рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями на местности – провешиванием прямых, делением отрезков и углов, построение перпендикуляров, параллельных прямых и т.д. Рассмотрены задачи и даны их решения.

Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ. Ценно то, что для их решения не требуется знаний больших, чем в объеме 8 классов. Решение геометрических задач на построение ограниченным набором инструментов используемых в данной работе роднит их с классическими задачами на построение с помощью циркуля и линейки изучаемые в школьном курсе геометрии.

Таким образом, поставленная цель: изучение некоторых методов решения геометрических задач на местности с помощью циркуля и короткой градуированной веревки, а также применение знаний по геометрии к решению практических задач на местности нами достигнута.

Задачи поставленные в начале работы – выполнены, гипотеза подтвердилась и мы нашли решение некоторых геометрических задач на построение используя только циркуль и короткую градуированную веревку.

Нами были решены основные задачи на построение, на основе которых решаются и другие задачи на построение.

Кроме того, рассмотрев задачи на построение с помощью циркуля и линейки и сравнив их с задачами на построение с помощью циркуля и короткой градуированной веревки, мы можем предположить, что данные множества задач совпадают.

Решение: данная работа может служить учителям прекрасным пособием для проведения факультативных занятий по математики и учащимся для более глубокого изучения геометрии.

Литература

1. Боженкова Л.И. Алгоритмический подход к решению задач на построение (VII-VIII классы) – Омск: Изд-во областного ИУУ, 1989.

2. Геометрия, 7-9: учеб. для общеобразоват. учреждений / [Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.]. – 18-е изд. – М.: Просвещение, 2008.

3. Час занимательной математики / под ред. Л.Я. Фальке. М.: Илекса; Народное образование; Ставрополь: Сервисшкола, 2003.

4. Шарыгин И.Ф., Егражиева Л.Н. Наглядная геометрия. М.: МИРОС, КПЦ “Марта”, 1992.