а) передатну функцію розімкненої САК визначимо як добуток передатних функцій усіх ланцюгів САК, оскільки маємо послідовне з’єднання ланцюгів. Таким чином

w(s)=w_ир(s)·w_ун(s)·w_ум(s)·w_ид(s)·w_р(s) = ,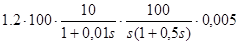

w(s) = .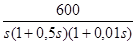

Схема розімкненої САК зображена на рис. 3.

б) передатну функцію замкненої САК отримаємо за формулою

Ф(s) = :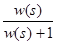

Ф(s) = .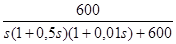

Зображення схеми замкненої САК зображена на рис. 4.

Визначимо стійкість системи по критерію Гурвіца

Знаючи перехідну функцію, знайдемо характеристичне рівняння системи:

D(s)= .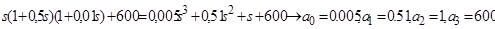

На основі отриманих коефіцієнтів характеристичного рівняння побудуємо головний визначник Гурвіца:

D = .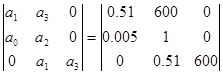

За критерієм Гурвіца для того, щоб система автоматичного керування була стійкою, необхідно та достатньо, щоб при а₀>0 всі визначники Гурвіца були додатними. Умовою стійкості для системи третього порядку будуть: а₁·a₂>a₀·a₃.

В даному випадку: а₀ = 0,005 > 0; а₁·a₂ = 0,51·1 = 0,51; a₀·a₃ = 0,005·600 = 3; 0,51<3. Умова стійкості системи не виконуються, отже за критерієм Гурвіца САК нестійка.

Побудова амплітудно-фазової частотної характеристики (АФЧХ) та визначення стійкості САК за критерієм Найквіста. Дослідження системи методом D – розбиття

а). Побудуємо амплітудно-частотну характеристику в визначимо стійкість системи по критерію Найквіста:

1) запишемо перехідну характеристику розімкнутої САК

w(s)= .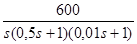

2) в рівнянні перехідної функції проведемо заміну s→j·ω та проведемо всі можливі перетворення та спрощення, тоді

w(j·ω) =  =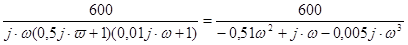

 = = .

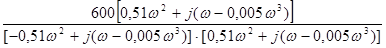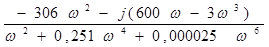Дійсна частина цього виразу

Re(w(j·ω)) = 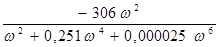 = Х(ω),

уявна частина – Im(w(j·ω)) = 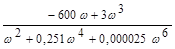 = У(ω).

3) Побудуємо на комплексній площині (Х0У) криву Найквіста та зробимо висновок про стійкість системи:

У(ω) = 0 → ω = 0 → Х(0) = 0;

У(ω) = 0 → ω = 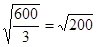=14 →

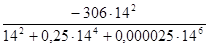Х(14) =  = -6.

По цим точкам побудуємо криву Найквіста (рис. 5).

Критерій Найквіста: Для того щоб замкнута система була стійкою необхідно, щоб годограф розімкненої системи починаючись на дійсній вісі і рухаючись проти годинникової стрілки (при змінній частоті від 0 до ∞) не охоплював точку (-1, j0).

Замкнена САК охоплює точку (-1, j0), що видно на рис. 5. Отже, САК нестійка.

б). Дослідження системи методом D – розбиття

За даними, що були отримані в пункті 3.3 знайдемо критичний коефіцієнт підсилення системи k_кр:

0,51 ≥ k·0,005

k ≤ 102

k = 102 (теоретично розрахований коефіцієнт підсилення).

Використовуючи методику D-розбиття та за допомогою програми MathCad побудуємо межу D-розбиття, обравши за параметр дослідження коефіцієнт підсилення системи.

Характеристичний поліном САК, враховуючи, що параметр, який досліджується, коефіцієнт підсилення:

D(p) = .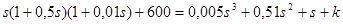

Звідси k(p) = 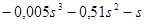 і k(ωj) =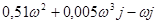

Побудуємо область D-розбиття, знаючи, що Re(k) = 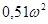, Im(k) = = 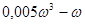(див. рис. 6).

На побудованій області D- розбиття можна визначити коефіцієнт підсилення (точка перетину області з дійсною віссю).