Содержание.
1. Основы квантовой механики атома. Соотношение де Бройля. Уравнение Шредингера..................................................................................................... 3
2. Ионная (гетерополярная) связь. Расчет энергии ионной связи................ 6
3. Теория ковалентной (гомеополярной) связи. Метод валентных связей... 8
4. Теория ковалентной связи. Метод молекулярных орбиталей (МО)...... 12
5. Упрощенный метод МО Хюккеля............................................................ 15
6. Особенности квантово-химических методов............................................ 16
7. Некоторые полуэмпирические методы.................................................... 17
8. Приближения молекулярной механики, лежащие в основе квантово-химических методов.......................................................................................................... 19
Литература.................................................................................................... 21
Упрощенный метод МО Хюккеля.
Вариант метода МО, предложенный Хюккелем (МОХ), содержит довольно грубые допущения и, как правило, не позволяет осуществлять точные расчеты. Несмотря на это, он часто используется в органической химии при качественном рассмотрении строения соединений с сопряженными связями, для сопоставления их свойств и предсказывания реакционной способности.
Главной особенностью метода МОХ является π-электронное приближение, в соответствии с которым молекулы, имеющие σ- и π-связи, рассчитывают лишь с учетом π-электронов. σ-электроны предполагаются локализованными возле приближенных ядер и не рассматриваются. Для всех атомов, образующих π-связи, π-электроны считаются общими и делокализованными во всем пространстве, занимаемом этими атомами. Волновая функция и уравнение Шредингера записываются лишь для π-электронов, а σ-электроны включаются в ядерный остов, движение которого не учитывается.
Кроме π-электронного приближения, в методе МОХ используется следующими допущениями:
1) кулоновские интегралы одинаковых атомов считают равными:
Jii = Jij = α;
2) резонансные интегралы одинаковых соседних атомов считают равными друг другу, а более удаленных – равными нулю:
kij = β (при j ± 1); kij = 0 (при i>j+1 и i<j+1).
3) интегралы непрерывания принимают равными нулю Sij = 0 (при i ≠ j);
нормировочные интегралы Sii = Sij = 1.
Особенности квантово-химических методов.
Методы современной квантовой химии распространяются на все более сложные объекты.
Общие принципы квантово-химических расчетов во всех случаях остаются сходными. Каждый объект с позиций метода МО считается единой системой, подчиняющейся законам квантовой механики. Обычно применяются адиабатическое и одноэлектронное приближения, вариант ЛКАОМО, вариационный метод с уравнениями Гутана. Кроме метода ССП (самосогласованного поля) и теории возмущений используется целый ряд упрощенных так называемых полуэмпирических методов.
Появление последних связано с тем, что последовательное применение метода МО к различным молекулярным объектам связано с большими вычислительными трудностями. С ростом количества частиц системы сильно увеличивается число членов уравнения Шредингера, отражающих потенциальную энергию их взаимодействия, а потому и количество подлежащих решению волновых уравнений.
В настоящее время наметилось два пути развития квантовой химии. Один из них – неэмпирический – предполагает минимальное привлечение экспериментальных данных и наиболее полный расчет с использованием орбиталей всех электронов исследуемой системы. Его недостатком являются нарастающие вычислительные трудности при увеличении сложности системы.
Другой путь реализуется с помощью различных полуэмпирических методов, которые используют дополнительные приближения – учитывают не все, а лишь валентные электроны или даже часть из них, как в методе МОХ; интегралы, появляющиеся в расчетах, либо принимаются за нуль, либо считаются независящими от положения атомов в молекуле и определяются из опыта или расчетов и т.д. Такие методы не столь сложны и целесообразны для сравнительной оценки свойств однотипных соединений.
Литература.
1. Минкин В.И. и др. Квантовая химия органических соединений. – М. Химия, 1986.
2. Кларк Т. Молекулярная механика. – М.: "Мир", 1990.
3. Краснов К.С. Молекулы и химическая связь. – М.: Химия, 1984.
4. Шустович С.М. Химическая связь. – М.: Наука, 1973.
Содержание.
1. Основы квантовой механики атома. Соотношение де Бройля. Уравнение Шредингера..................................................................................................... 3
2. Ионная (гетерополярная) связь. Расчет энергии ионной связи................ 6
3. Теория ковалентной (гомеополярной) связи. Метод валентных связей... 8
4. Теория ковалентной связи. Метод молекулярных орбиталей (МО)...... 12
5. Упрощенный метод МО Хюккеля............................................................ 15
6. Особенности квантово-химических методов............................................ 16
7. Некоторые полуэмпирические методы.................................................... 17
8. Приближения молекулярной механики, лежащие в основе квантово-химических методов.......................................................................................................... 19
Литература.................................................................................................... 21
Основы квантовой механики атома. Соотношение де Бройля. Уравнение Шредингера.
Химические процессы сводятся к превращению молекул, т.е. к возникновению и разрушению связей между атомами. Поэтому важнейшей проблемой химии всегда была и остается проблема химического взаимодействия, тесно связанная со строением и свойствами вещества. Современная научная трактовка вопросов химического строения и природы химической связи дается квантовой механикой – теорией движения и взаимодействия микрочастиц (электронов, ядер и т.д.).
Одним из общих свойств материи является ее двойственность. Частицы материи обладают одновременно и корпускулярными и волновыми свойствами. Соотношение "волна – частица" таково, что с уменьшением массы частицы ее волновые свойства все более усиливаются, а корпускулярные – ослабевают. Когда же частица становится соизмеримой с атомом, наблюдаются типичные волновые явления. Одновременно оказывается невозможным описание движения и взаимодействия микрочастиц-волн законами движения тел с большой массой. Первый шаг в направлении создания волновой, или квантовой механики, законы которой объединяют и волновые, и корпускулярные свойства частиц, сделал де Бройлем (1924). Де Бройль высказал гипотезу, что с каждой материальной частицей связан некоторый периодический процесс. Если частица движется, то этот процесс представляется в виде распространяющейся волны, которую называют волной де Дройля, или фазовой волной. Скорость частицы V связана с длиной волны λ соотношением де Бройля:
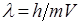 (1)
(1)
где m – масса частицы (например, электрона);
h – постоянная Планка.
Уравнение (1) относится к свободному движению частиц. Если же частица движется в силовом поле, то связанные с ней волны описываются так называемой волновой функцией. Общий вид этой функции определил Шредингер (1926). Найдем волновую функцию следующим путем. Уравнение, характеризующее напряженность поля Еа плоской монохроматической волны света, можно записать в виде:
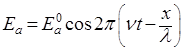 , (2)
, (2)
где Еа0 – амплитуда волны;
ν – частота колебаний;
t – время;
λ – длина волны;
х – координата в направлении распространения волны.
Так как вторые производные от уравнения плоской волны (2), взятые по времени t и координате х, равны соответственно:
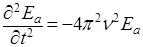 , (3)
, (3)
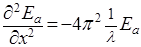 , (4)
, (4)
то 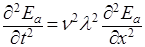
Подставляя λ=с/ V (с – скорость света), получаем волновое уравнение для плоской световой волны:
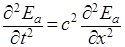 , (5)
, (5)
Последующие преобразования основываются на предположениях, что распространение волн де Бройля описывается аналогичным уравнением, и что эти волны становятся стационарными и сферическими. Сначала представим, что по уравнению (5) изменяется значение новой функции ψ от координат (χ, y, z), имеющей смысл амплитуды некоторого колебательного процесса. Тогда, заменяя Еа на ψ, получим волновое уравнение в форме:
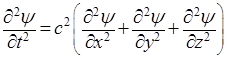 , (6)
, (6)
После исключения t (с помощью (3)) волновое уравнение примет вид:
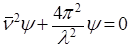 , (7)
, (7)
где ψ – так называемая волновая функция – величина, периодически изменяющаяся по закону гармонического движения;
ν2 – оператор Лапласа, означающий, что над функцией производится следующее действие:
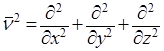 .
.
Будем считать, что волновое уравнение (7) описывает движение частицы. Тогда λ – длина фазовой волны, а ψ – амплитуда фазовой волны в любой произвольно взятой точке χ, y, z, характеризующей местоположение частицы. Длину и амплитуду фазовой волны можно связать с массой и энергией частицы. Если частица движется в потенциальном поле, то ее полная энергия Е складывается из кинетической энергии Ек = mV2/2 и потенциальной энергии Еп. Отсюда
½mV2 – Е – Еп или m2V2 = 2m(E – Eп).
Учитывая соотношение де Бройля, запишем
m2V2 = h2/λ2 и λ2 = h2/2m (E – Eп)
и представим волновое уравнение в следующем виде:
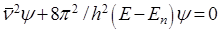 (8)
(8)
В этой форме волновое уравнение называется уравнением Шредингера. Оно является основным уравнением квантовой механики.
Уравнение Шредингера – дифференциальное уравнение в частных производных и может иметь множество решений. Однако физический смысл имеют лишь те ψ-функции (так называемые собственные функции), которые удовлетворяют ряду условий. Во-первых, эти функции должны быть непрерывными, конечными, однозначными и обращаться в нуль на бесконечном расстоянии. Наложение перечисленных условий называется нормированием ψ-функции. Во-вторых, собственным ψ-функциям соответствуют не любые, а только дискретные значения полной энергии Е. Как дискретные значения энергии, так и вид собственных ψ-функций определяется совокупностью квантовых чисел n, l, m, которые хотя и не содержатся в самом уравнении Шредингера, но вводятся в него при решении. Таким образом, квантование энергии естественно и неизбежно вытекает из основных свойств материальных объектов и не нуждается в особом постулировании, которое было сделано Н. Бором при разработке планетарной модели атома.
Дата: 2019-05-28, просмотров: 258.