Линейные размеры тел в движущейся системе отсчёта сокращаются.

Парадокса шеста и сарая:

Из СТО мы знаем, что движущиеся тела сокращаются в направлении движения. Возьмём сарай с двумя сквозными дверьми. Возьмём шест, который чуть длиннее, чем сарай. Если открыть обе двери и просунуть в них шест, то он в сарай не поместится и будет торчать из дверей по обе стороны. Воспользуемся сокращением длин — разгоним шест до такой скорости, чтобы он сократился, допустим в два раза, и тогда, пролетая сквозь сарай, он весь целиком там поместится! Захлопнем двери сарая, пока шест находится внутри и тут же быстренько их откроем, чтобы не поломать шест. И мы видим следующее противоречие: система отсчёта, связанная с шестом, такая же равноправная, как и связанная с сараем. То есть, в ней будут наблюдаться те же эффекты сокращения продольных размеров, но только уже сарая! В ней сарай станет короче, и чуть более длинный изначально шест станет еще более длинным и никогда в сарай не поместится. Значит, захлопнув двери сарая, мы обязательно сломаем шест!

Этот парадокс — один из типичных случаев, когда, вцепившись в один из эффектов СТО, человек делает далеко идущие выводы, пренебрегая другими, подчас более важными, эффектами. Сокращение длин действительно произойдет так, как описано в парадоксе — для сарая шест окажется укороченным и поместится в нём целиком, а для шеста — сарай окажется укороченным и не сможет поместить в себя весь шест. Так где же правда?

А правда — в относительности одновременности. Сокращение длин — это второстепенный эффект, относительность же одновременности — намного же более важный. Ещё раз вспомним уже сказанное тут: события, одновременные в одной системе отсчета, будут по СТО неодновременными в другой системе отсчёта, если системы движутся друг относительно друга. Если присмотреться к эксперименту, у нас в нём есть чётко выраженные события, одновременные в ИСО сарая — это момент, когда мы закрываем переднюю и заднюю двери сарая. Мы делаем это в ИСО сарая ОДНОВРЕМЕННО. Нетрудно догадаться, что в ИСО шеста они произойдут в разные моменты времени, а именно: когда передний конец шеста войдет в сарай и приблизится к задней двери, она захлопнется и тут же откроется, а когда задний конец шеста сравняется с передней дверью, захлопнется и откроется, в свою очередь, и она. Таким образом, шест не сломается ни в ИСО сарая, ни в ИСО шеста. Если внимательно присмотреться к этому парадоксу, то можно сделать один важный вывод насчёт эффекта сокращения длин. Как мы измеряем длину объекта? Прикладываем к нему линейку и смотрим на показания шкалы у начала и конца объекта. А что если этот объект двигается? Тогда, чтобы не испортить показания, посмотреть на шкалу у начала и конца объекта надо одновременно, а иначе показания окажутся неверными. Но ведь то, что в нашей ИСО по теории относительности одновременно, в другой ИСО будет неодновременным.

Парадокс диска:

Рассмотрим велосипедное колесо, которое крутится с большой скоростью. Каждый элемент спицы движется перпендикулярно своей длине и сокращения в продольном измерении не испытывает. Значит, не испытывает сокращения и вся спица. С другой стороны, каждый элемент обода движется вдоль своей длины и сокращается. Таким образом, отношение длины окружности к её радиусу меняется.

Разгадка в том, что каждый элемент колеса движется ускоренно, и СТО тут малоприменимо. В ОТО же непостоянность числа π совершенно нормальна.

О релятивистской массе

Так называемая релятивистская масса движущегося объекта определяется соотношением (верным и для частиц, движущихся со скоростью света):

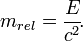
Релятивистская масса движущегося объекта больше массы покоя:

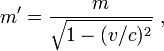
и возрастает с увеличением скорости. «Утяжеление» следует понимать лишь условно, так как второй закон Ньютона в форме F = m'a всё равно не выполняется (направление ускорения в общем случае не совпадает с направлением силы).

В современной физической литературе по СТО, однако, принято, что m — масса частицы (инвариантная масса) не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной. Понятие «релятивистской массы» не используется и не рекомендуется к применению, хотя оно и встречается в ранних работах по теории относительности.

Исторический очерк

В 1728 году английский астроном Брэдли открыл аберрацию света: все звёзды описывают на небосводе малые круги с периодом в один год. С точки зрения эфирной теории света это означало, что эфир неподвижен, и его кажущееся смещение (при движении Земли вокруг Солнца) по принципу суперпозиции отклоняет изображения звёзд. Френель, однако, допускал, что внутри вещества эфир частично увлекается. Эта точка зрения, казалось, нашла подтверждение в опытах Физо, который обнаружил, что скорость света в воде зависит от направления её движения: вдоль течения скорость света больше, чем против течения.

Максвелл в 1868 году предложил схему решающего опыта, который после изобретения интерферометра смог осуществить в 1881 году американский физик Майкельсон. Позже Майкельсон и Эдуард Морли повторили опыт несколько раз с возрастающей точностью, но результат был неизменно отрицательным — «эфирного ветра» не существовало.

В 1892 году Лоренц и (независимо от него) Джордж Фитцджеральд предположили, что эфир неподвижен, а длина любого тела сокращается в направлении его движения. Одновременно изучался вопрос, при каких преобразованиях координат уравнения Максвелла инвариантны. Правильные формулы впервые выписали Лармор (1900) и Пуанкаре (1905), последний доказал их групповые свойства и предложил назвать преобразованиями Лоренца.

Пуанкаре также дал обобщённую формулировку принципа относительности, охватывающего и электродинамику. Тем не менее он продолжал признавать эфир, хотя придерживался мнения, что его никогда не удастся обнаружить — см. доклад Пуанкаре на физическом конгрессе, 1900 год^[2]. В этом же докладе Пуанкаре впервые высказывает мысль, что одновременность событий не абсолютна, а представляет собой условное соглашение («конвенцию»). Было высказано также предположение о предельности скорости света.

Под влиянием критики Пуанкаре Лоренц в 1904 году предложил новый вариант своей теории. В ней он предположил, что при больших скоростях механика Ньютона нуждается в поправках. В 1905 году Пуанкаре далеко развил эти идеи в статье «О динамике электрона». Предварительный вариант статьи появился в 1895 году в Comptes Rendus, развёрнутый был закончен в июле 1905 года, опубликован в январе 1906 года, почему-то в малоизвестном итальянском математическом журнале.

В этой итоговой статье формулируется всеобщий принцип относительности с преобразованиями Лоренца для всех явлений (не только электромагнитных). Пуанкаре нашёл выражение для четырёхмерного интервала как инварианта преобразований Лоренца: r² + (ict)². Он даже предложил нечто вроде релятивистского обобщения теории гравитации; в его теории тяготение распространялось в эфире со скоростью света.

Таким образом, в начале XX века существовали две несовместимые кинематики: классическая, с преобразованиями Галилея, и электромагнитная, с преобразованиями Лоренца. Эйнштейн, размышляя на эти темы, предположил, что первая есть приближённый случай второй для малых скоростей, а то, что считалось свойствами эфира, есть на деле проявление объективных свойств пространства и времени. Эйнштейн пришёл к выводу, что нелепо привлекать понятие эфира только для того, чтобы доказать невозможность его наблюдения. В своей основополагающей статье «К электродинамике движущихся сред» (1905) он предложил два постулата: специальный принцип относительности и постоянство скорости света; из них без труда выводятся лоренцево сокращение, формулы преобразования Лоренца, относительность одновременности, ненужность эфира, новая формула суммирования скоростей, возрастание инерции со скоростью и т. д. В последующих работах появилась и формула E₀ = mc² — масса определяется энергией покоя.

Часть учёных сразу приняли СТО: Планк (1906) и сам Эйнштейн (1907) построили релятивистскую динамику и термодинамику. Минковский в 1907 году представил математическую модель кинематики СТО, в которой преобразования Лоренца вытекают из геометрии четырёхмерного псевдоевклидова пространства: в пространстве Минковского, лоренцевы преобразования являются преобразованиями поворотов координатных осей.

Были, однако, и критики новых концепций. Они указывали на то, что теория относительности не предсказывает новых фактов, которые можно проверить экспериментально, и ничем не лучше теории Лоренца. Появились попытки найти в СТО внутренние противоречия. Концепцию эфира продолжали поддерживать Дж. Дж. Томсон, Ленард, Лодж и другие известные физики. Сам Лоренц прекратил критику СТО только к концу жизни; свои разногласия с теорией относительности он сам сформулировал так:

Основная причина, по которой я не смог предложить теории относительности, заключается в том, что я придерживался представления, будто лишь переменная t может считаться истинным временем, а предложенное мной местное время t' должно рассматриваться только в качестве вспомогательной математической величины.

С 1911 года Эйнштейн разрабатывал общую теорию относительности (ОТО), включающую гравитацию, на основе принципа эквивалентности, которую завершил в 1916 году.

В 1930-е годы был проведен ряд экспериментов для проверки главного постулата СТО — постоянства скорости света. Некоторые измерения (Миллер и др.) поставили его под сомнение, однако точные эксперименты Мак-Кеннеди подтвердили этот факт. Постепенно накапливались опытные подтверждения СТО. На ней основаны квантовая теория поля, теория ускорителей, она учитывается при проектировании и работе спутниковых систем навигации (здесь оказались нужны даже поправки общей теории относительности) и др.

Ряд экспериментов по проверке эффектов СТО и ОТО был проведен в конце XX века; их результаты находятся в полном согласии с теорией. Тем не менее исследования с целью найти границы применимости теории относительности продолжаются.

Заключение

Общая теория относительности, в настоящее время — самая успешная теория, хорошо подтверждённая наблюдениями. Первый успех общей теории относительности состоял в объяснении аномальной прецессии перигелия Меркурия. Затем, в 1919 году, Артур Эддингтон сообщил о наблюдении отклонения света вблизи Солнца в момент полного затмения, что качественно и количественно подтвердило предсказания общей теории относительности. С тех пор многие другие наблюдения и эксперименты подтвердили значительное количество предсказаний теории, включая гравитационное замедление времени, гравитационное красное смещение, задержку сигнала в гравитационном поле и, пока лишь косвенно, гравитационное излучение. Кроме того, многочисленные наблюдения интерпретируются как подтверждения одного из самых таинственных и экзотических предсказаний общей теории относительности — существования чёрных дыр

Так же, как и в случае квантовой механики, многие предсказания теории относительности противоречат интуиции, кажутся невероятными и невозможными. Это, однако, не означает, что теория относительности неверна. В действительности, то, как мы видим (либо хотим видеть) окружающий нас мир и то, каким он является на самом деле, может сильно различаться. Уже больше века учёные всего мира пробуют опровергнуть СТО. Ни одна из этих попыток не смогла найти ни малейшего изъяна в теории. О том, что теория верна математически, свидетельствует строгая математическая форма и чёткость всех формулировок.

О том, что СТО действительно описывает наш мир, свидетельствует огромный экспериментальный опыт. Многие следствия этой теории используются на практике. Очевидно, что все попытки «опровергнуть СТО» обречены на провал потому, что сама теория опирается на три постулата Галилея (которые несколько расширены), на основе которых построена ньютонова механика, а также на дополнительный постулат о постоянстве скорости света во всех системах отсчета. Все четыре не вызывают какого-либо сомнения в пределах максимальной точности современных измерений: лучше 10 ^{− 12}, а в некоторых аспектах — до 10 ^{− 15}. Более того, точность их проверки является настолько высокой, что постоянство скорости света положено в основание определения метра — единицы длины, в результате чего скорость света становится константой автоматически.

Список литературы

· Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7

· Паули В. Теория относительности. Изд. 2-е, испр. и доп. Перев. с нем. — М.: Наука, 1983. — 336 с.

· Спасский Б. И.. История физики. Том 2, часть 2-я. М.: Высшая школа, 1977.

· Эйнштейн А. Сущность теории относительности. — М.: Изд. ин. лит., 1955. — 157 с.

· Уиттекер Э. История теории эфира и электричества. Современные теории 1900-1926. Пер с англ. Москва, Ижевск: ИКИ, 2004. 464с. ISBN 5-93972-304-7 (Глава 2)

· Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900–1915). М.: Наука, 1981. - 352c.

· Герман Вейль. Пространство. Время. Материя. Лекции по общей теории относительности. — М.: Изд-во УРСС научной и учебной литературы, 2004. 455 с.

· Дирак П. А. М. Общая теория относительности М.: Атомиздат, 1978.

· Фок В. А. Теория пространства, времени и тяготения / 2-е изд. М.: ГИФМЛ, 1961.

· Толмен Р. Относительность, термодинамика и космология М.: Наука, 1974.

· Пенроуз Р. Структура пространства-времени М.: Мир, 1972.

· Мизнер Ч., Торн К., Уилер Дж. Гравитация. М.: Мир, 1977. Том 1 Том 2 Том 3

· Хокинг С., Эллис Дж. Крупномасштабная структура пространства-времени М.: Мир, 1977.

· Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). М.: Наука, 1981. — 352 c.

· Визгин В. П. Единые теории в 1-й трети ХХ в. М.: Наука, 1985. — 304 c.

· http://www.wikipedia.ru

· http://www.lurkmore.ru