Промоделируем в пакете математического моделирования MatLab метод Волдера «Цифра за цифрой» для анализа его работоспособности и определения погрешности вычислений.
В цикле подсчитаем значение абсолютной погрешности при изменении количества итераций от 1 до n и при изменении разрядности данных (дробная часть задается от 1 до 16 бит).
Листинг программы для исследования погрешности при изменении числа итераций:
//== function arch ====
//function [archZ] = arch(Z,N)
Q0 = 0;
x0 = 0.6072529;
y0 = 0;
N=20;
Z= 0.512
acos_ist = asin(Z)
for n=1:N
Q(1)=Q0+atan(2^(-0));
r(1)=sign(Z-y0);
x(1)=x0-y0*2^(-0);
y(1)=y0+x0*2^(-0);
for i=1:n
r(i)=sign(Z-y(i));
// ARTH =atan(2^(-i));
Q(i+1)= Q(i)+r(i)*atan(2^(-i));
x(i+1)= x(i)-r(i)*y(i)*2^(-i);
y(i+1)= y(i)+r(i)*x(i)*2^(-i);
end
arcsinZ(n)= Q(n);
asin_ist = asin(Z);
pogr(n)=(asin_ist-arcsinZ(n))/asin_ist*100;
end
scf(1);
clf();
plot(pogr);
xgrid();
//endfunction
//////////////////////////////////////////////////////////////
Q0 = 0;
x0 = 0.6072529;
y0 = 0;
for n=1:20
m=3;
Q(1)=Q0+atan(2^(-0));
Q(1)=conv(n,m,Q(1));
r(1)=sign(Z-y0);
x(1)=x0-y0*2^(-0);
x(1)=conv(n,m,x(1));
y(1)=y0+x0*2^(-0);
y(1)=conv(n,m,y(1));
for i=1:20
r(i)=sign(Z-y(i));
// ARTH =atan(2^(-i));
Q(i+1)= Q(i)+r(i)*atan(2^(-i));
Q(i+1)=conv(n,m,Q(i+1));
x(i+1)= x(i)-r(i)*y(i)*2^(-i);
x(i+1)=conv(n,m,x(i+1));
y(i+1)= y(i)+r(i)*x(i)*2^(-i);
y(i+1)=conv(n,m,y(i+1));
end
arcsinZ(n)= Q(20);
asin_ist = asin(Z);
pogr(n)=(asin_ist-arcsinZ(n))/asin_ist*100;
end
scf(2);
clf();
plot(pogr);
xgrid();
Запустив приведенную программу, мы получим график зависимости погрешности от числа итераций:
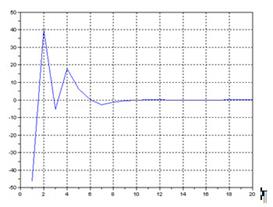
Рис.1.1 - График абсолютной погрешности для функции Θ = arcsin Z при изменяющемся числе итераций
По полученным графикам видно как ведёт себя погрёшность преобразования. При количестве итераций меньше 10 погрешность достигает 5%. По заданию требуется, чтобы погрешность составляла меньше 1%, это достигается при n = 13 и более.
Листинг программы для изменения разрядности данных:
clear
clc
//== function convert real to bin ====
function [x_bin] = conv(n,m,x)
//преобразование целой части
x_int = abs(int(x));
x_tmp=x_int;
for j=1:m
x_tmp = x_tmp/2
if (x_tmp-int(x_tmp))==0
arr_tmp(j)=0
else
arr_tmp(j)=1
x_tmp = int(x_tmp)
end
end
x_cel = 0;
for j=1:m
x_cel = x_cel+arr_tmp(j)*2^(j-1)
end
//преобразование дробной части
x_real = x- x_int;
for i=1:n,
x_real = x_real * 2;
if x_real<1
arr(i)=0;
else
arr(i)=1;
x_real=x_real-1;
end,
x_real1=1-int(x_real)
end
x_new=0;
for i=1:n
x_new=x_new+arr(i)*2^(-i)
end
x_bin=x_cel+x_new
endfunction
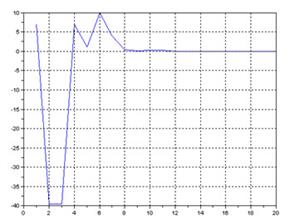
Рис.1.2 - График абсолютной погрешности для функции Θ = arch Z при изменении разрядности дробной части
Изменяя количество бит, приходящихся на дробную часть, исследуется влияние разрядности данных на точность вычислений. Из графика видно, что необходимая точность достигается при разрядности дробной части 13 и более.
Исследуем точность итерационных формул для функции arcth Z в математическом пакете SciLab. Ниже приведен код программы, которая вычисляет погрешность вычисления методом Волдера заданной функции при изменении числа итерации и разрядности дробной части.
Листинг программы :
clear
clc
//== function convert real to bin ====
function [x_bin] = conv(n,m,x)
//преобразование целой части
x_int = abs(int(x));
x_tmp=x_int;
for j=1:m
x_tmp = x_tmp/2
if (x_tmp-int(x_tmp))==0
arr_tmp(j)=0
else
arr_tmp(j)=1
x_tmp = int(x_tmp)
end
end
x_cel = 0;
for j=1:m
x_cel = x_cel+arr_tmp(j)*2^(j-1)
end
//преобразование дробной части
x_real = x- x_int;
for i=1:n,
x_real = x_real * 2;
if x_real<1
arr(i)=0;
else
arr(i)=1;
x_real=x_real-1;
end,
x_real1=1-int(x_real)
end
x_new=0;
for i=1:n
x_new=x_new+arr(i)*2^(-i)
end
x_bin=x_cel+x_new
endfunction
//========================================
function [arth_i]=arth(x)
arth_i = 1/2*log((1+x)/(1-x));
endfunction
//== function arcth ====
//function [arcthZ] = arcth(Z,N)
Q0 = 0;
x0 = 1;
Z=2.25;
y0 = Z;
N=40;
Q(1)=Q0+arth(2^(-1));
r(1)=sign(1-y0);
x(1)=x0-r(1)*y0*2^(-1);
y(1)=y0-r(1)*x0*2^(-1);
for n=1:N
for k=2:n
i=1+int((k-1)/2);
r(k)=sign(1-y(k-1));
ARTH =arth(2^(-i));
Q(k)= Q(k-1)+r(k)*ARTH;
x(k)= x(k-1)-r(k)*y(k-1)*2^(-i);
y(k)= y(k-1)-r(k)*x(k-1)*2^(-i);
end
arthZ(n)= Q(n)
y_ist = 1/2*log((1+Z)/(1-Z))
// z_i = (exp(y_ist)+exp(-y_ist))/2
pogr(n)=(y_ist-arthZ(n))/y_ist*100;
end
scf(1);
clf();
plot(pogr);
xgrid();
//endfunction
for n=1:20
m=3;
Q(1)=Q0+arth(2^(-1));
Q(1)=conv(n,m,Q(1));
r(1)=sign(Z-x0);
x(1)=x0+r(1)*y0*2^(-1);
x(1)=conv(n,m,x(1));
y(1)=y0+r(1)*x0*2^(-1);
y(1)=conv(n,m,y(1));
last=26;
for k=2:last
i=1+int((k-1)/2);
r(k)=sign(Z-x(k-1));
ARTH =arth(2^(-i));
ARTH=conv(n,m,ARTH);
Q(k)= Q(k-1)+r(k)*ARTH;
Q(k)=conv(n,m,Q(k));
x(k)= x(k-1)+r(k)*y(k-1)*2^(-i);
x(k)=conv(n,m,x(k));
y(k)= y(k-1)+r(k)*x(k-1)*2^(-i);
y(k)=conv(n,m,y(k));
end
archZ(n)= Q(last);
y_ist = log(Z+sqrt(Z^2-1));
pogr(n)=(y_ist-archZ(n))/y_ist*100;
end
scf(2);
clf();
plot(pogr);
xgrid();
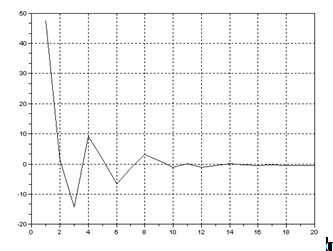
Рис.1.3 - График абсолютной погрешности для функции arcthZ при изменяющемся числе итераций
Рис.1.4 - График абсолютной погрешности для функции arcthZ при изменении разрядности дробной части
Из приведенных графиков видно, что минимальное число итерации должно составить 12, а минимальное число разрядов – 12. То есть рассчитанное число итераций и разрядность данных соответствуют результатам моделирования.
Дата: 2019-05-28, просмотров: 306.