Для решения задачи МЕТОДА.
Нажождение корня уравнения методом дихотомии.
Считаем, что на отрезке [а, b] расположен один корень, который необходимо уточнить с погрешностью e.
Метод дихотомии, или половинного деления, заключается в следующем. Определяем середину отрезка [а, b]
Х= (а + b)/2
и вычисляем функцию f(Х). Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f ( x ) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f ( x ) имеет разные знаки.Это будет отрезок [а, Х], т.е. для очередного шага уточнения точку b перемещаем в середину отрезка Х и продолжаем процесс деления как с первоначальным отрезком [а,b].
Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока интервал [а,b] не станет меньше заданной погрешности e.
Следует учитывать, что функция f ( x ) вычисляется с некоторой абсолютной погрешностью e1. Вблизи корня значения функции f ( x ) малы по абсолютной величине и могут оказаться сравнимыми с погрешностью ее вычисления. Другими словами, при подходе к корню мы можем попасть в полосу шумов 2e1 и дальнейшее уточнение корня окажется невозможным. Поэтому надо задать ширину полосы шумов и прекратить итерационный процесс при попадании в нее. Также необходимо иметь в виду, что при уменьшении интервала [а,b] увеличивается погрешность вычисления его длины (b – а) за счет вычитания близких чисел.
Метод дихотомии позволяет значительно уменьшить объем вычислений по сравнению с графическим методом. Так как за каждую итерацию интервал, где расположен корень, уменьшается в два раза, то через n итераций интервал будет равен (b - а)/2n. За 10 итераций интервал уменьшится в 2 10 =1024 раз, за 20 итераций - в 220=1048576 раз.
Описание алгоритма решения задачи и схема алгоритма.
Основная задача, которая решается в этой программе, это решение приведённого далее уравнения относительно 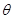 :
:
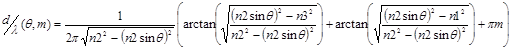 , (3.1)
, (3.1)
| где | 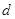 - толщина волновода; - толщина волновода;
|
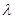 - длина волны запускаемого пучка света; - длина волны запускаемого пучка света;
| |
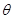 - направляющий угол; - направляющий угол;
| |
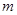 - порядок моды; - порядок моды;
| |
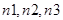 - показатели преломления волновода и окружающих его веществ. - показатели преломления волновода и окружающих его веществ.
|
В программе решение данного уравнения реализавано методом дихотомии, схема которого приведена ниже.
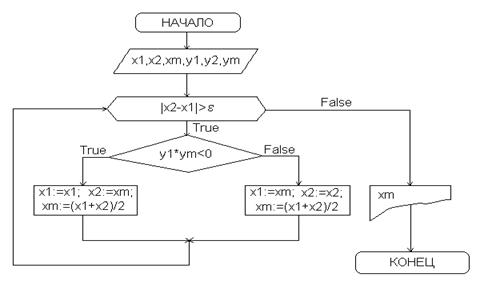 Рисунок 3.1 – блок-схема метода дихотомии.
Рисунок 3.1 – блок-схема метода дихотомии.
|
Далее, используя полученные значения направляющих углов, строится график, отображающий профили ТЕ-мод. График, отображающий правую часть уравнения (3.1), практической ценности для решения задачи не имеет и носит чисто иллюстративный характер.
ОПИСАНИЕ ПРОГРАММЫ.
Вид программы представлен на рисунке 4.1. По своей внешней форме она представляет собой 4 закладки, расположенные на 1 форме. На первой закладке осуществляется ввод исходных данных, на второй строится график дисперсионной характеристики волновода, на третьей выводятся значения направляющих углов, а на чётвертой строятся профили ТЕ-мод.
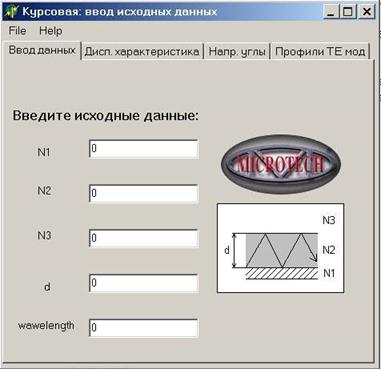 Рисунок 4.1 - Основной вид программы, закладка для ввода исходных данных.
Рисунок 4.1 - Основной вид программы, закладка для ввода исходных данных.
|
Все вычисления и построения графиков производятся при смене закладки с первой на любую другую (событие объекта TPageControl «OnChange»). Перед сменой (событие «OnChanging») осуществляется проверка на полноту исходных данных: если хоть в одном из окон осталось стоящее по умолчанию число «0», то смены закладки не произойдёт, зато возникнет информационное окно, которое укажет пользователю на его ошибку. При повторном переходе с первой закладки на другую будет произведён перерасчёт.
Вычисление направляющих углов осуществляется с указанной в задании точностью – 0,001.
Полная схема и листинг программы находятся в приложении А и В соответственно.
Дата: 2019-05-28, просмотров: 295.