АННОТАЦИЯ.
Пояснительная записка данного курсового проекта, тема которого "Моделирование работы цеха", содержит описание назначения и условий применения программы, описание задачи, общие сведения, функциональное назначение, описание логической структуры программы, используемые технические средства, описание вызова и загрузки, входные и выходные данные для программы, контрольный пример, инструкцию пользователю, текст программы, приложения с изображениями A-схемы и Q-схемы, блок-схемы и экранной формы программы, что вместе составляет 42 листа.
Для реализации алгоритма программы данного курсового проекта был выбран язык программирования Delphi версии 6.0. Существует много различных методов и программных средств для создания программного продукта. Среда визуального программирования выбрана с целью быстрого создания удобного и красивого интерфейса. Среда Borland Delphi выбрана потому, что она позволяет создавать достаточно сложные проекты без высокого уровня знаний самой среды. Среда визуального программирования Delphi позволяет создавать удобный и красивый интерфейс, не требуя при этом больших усилий. Такой интерфейс понятен в использовании любому пользователю, даже начинающему. Delphi позволяет использовать в программе рисунки, строить графики, использовать объекты офисных приложений, использовать мультимедийные эффекты.
При написании данного курсового проекта использовались различные литературные источники, которые перечислены в соответствующем разделе.
Данная работа написана в соответствие с данными варианта №2. Варианты заданий указаны в методическом пособии по написанию курсовой работы, указанном в списке использованной литературы под номером 1.
СОДЕРЖАНИЕ.
Введение
1. Описание применения:
1.1. Назначение и условия применения программы
1.2. Описание задачи
2. Описание программы:
2.1. Общие сведения и функциональное назначение.
2.2. Описание логической структуры
2.3. Используемые технические средства, вызов и загрузка
2.4. Входные и выходные данные
2.5. Контрольный пример
2.6. Инструкция пользователю
3. Текст программы:
3.1. Модуль 1.
3.2. Модуль 2
3.3. Модуль 3.
Список использованных источников
Приложение А.
Приложение Б.
Приложение В
Приложение Г
ВВЕДЕНИЕ.
Для того, чтобы приступить к детальному рассмотрению процесса создания программы данного курсового проекта, необходимо вначале рассмотреть основные термины и понятия, использующиеся в данной пояснительной записке. Прежде всего, следует обратить внимание на термин "моделирование". Сегодня, наверное, невозможно найти такую сферу деятельности человека, в которой в той или иной степени не использовались бы методы моделирования. Особенно это относится к сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации.
Методологическая основа моделирования – диалектико-математический метод познания и научного исследования. Все то, на что направлена человеческая деятельность, называется объектом (от лат. objectum – предмет). Выборка методологии направлена на упорядочения получения и обработки информации об объектах, которые существуют вне нашего сознания и взаимодействуют между собой и внешней средой.
Научно-техническое развитие в любой области обычно идет по пути: наблюдение и эксперимент – теоретические исследования – организация производственных процессов.
Аналогией называют суждение о каком-либо частном сходстве двух объектов. Причем такое сходство может быть существенным и несущественным.
Гипотезы и аналогии, отражающие реальный, объективно существующий мир, должны обладать наглядностью или сводиться к удобным для исследования логическим схемам: такие логические схемы, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений, называются моделями. Другими словами, модель (лат. modulus – мера) – это объект-заместитель объекта - оригинала, обеспечивающий изучение некоторых свойств оригинала.
Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называются моделированием: Таким образом, моделирование может быть определено как представление объекта моделью для получения информации об этом объекте путем проведения экспериментов с его моделью. Теория замещения одних объектов (оригиналов) другими объектами (моделями) и исследования свойств объектов на их моделях называется теорией моделирования.
Если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах, то говорят, что модель адекватна объекту. При этом адекватность модели зависит от цели моделирование и принятых критериев.
Модель – это целевое отображение. Следовательно, для разных целей создаются разные модели. Множество моделей делится на типы по целевому признаку:
1. Познавательные (цель теоретическая). Модели являются формой организации представления знаний, средством соединения новых знаний с имеющимися. Познавательные модели приближают модель к реальности.
2. Прагматические (цель практическая). Модели являются средством управления, средством организации практических действий или их результата. Является рабочим представлением цели, носит нормативный характер. Использование этих моделей состоит в том, чтобы при расхождении модели и реальности, изменить реальность так, чтобы приблизить реальность к модели.
Понятие моделирования практически неотделимо от понятия системы. Системой называется совокупность взаимодействующих элементов, обособленная от среды и взаимодействующая с ней как целое образование, имеющее новое свойство, отсутствующее у элементов системы. Наличие у системы нового свойства называется эмерджентностью.
Элемент системы – это объект, выполняющий функции и не разбиваемый далее в рамках задачи.
Цель системы – это субъективный образ (абстрактная модель) несуществующего, но желаемого состояния среды, которое решило бы проблему.
Согласно первому определению системы, система – это средство достижения цели. Система имеет следующие свойства:
1. Целостность: система имеет свойства, не присущие ее элементам.
2. Целенаправленность.
3. Множественность целей: несовпадение цели системы и целей отдельных компонентов.
4. Обособленность от среды.
5. Динамичность.
6. Абстрактный характер описания: исследуемая система, так или иначе, отличается от объекта наблюдения.
7. Принцип причинности. Это свойство присуще динамическим причинам. Отклик системы на некоторое воздействие не может начаться раньше, чем само воздействие.
Система, в которой происходит изменения со временем, называется динамической. Выделяют два вида динамики: функционирование и развитие. Функционирование – это процесс, происходящий в системе, стабильно реализующей фиксированную цель. Развитие – это то, что происходит с системой при изменении ее цели.
Написание данного курсового проекта позволяет закрепить знания, полученные в процессе изучения дисциплины "Основы теории систем и системного анализа". На этом предмете были изучены основные аспекты системного анализа, понятие о моделях и моделировании, понятие о системе, их классификацию, а также рассмотрены типовые математические схемы.
ОПИСАHИЕ ПРИМЕHЕHИЯ.
Описание задачи.
На обрабатывающий участок цеха поступают детали в среднем через 50 мин. Первичная обработка производится на одном из двух станков. Первый станок обрабатывает деталь в среднем 40 мин. и имеет до 4% брака, а второй станок обрабатывает деталь в среднем 60 мин. и имеет до 8% брака. Все детали возвращаются на повторную обработку на второй станок. Детали, который попали в разряд бракованных дважды, считаются отходами. Повторную обработку производят также два станка в среднем 100 мин. каждый. При этом первый станок обрабатывает присутствующие в накопителе после первичной обработки детали, а второй станок подключается при создании в накопителе очереди более трёх деталей. Все интервалы времени распределены по экспоненциальному закону.
Необходимо смоделировать обработку на участке 500 деталей, а также определить загруженность второго станка на повторной обработке и возможность появления отходов, определить возможность уменьшения очереди в накопителе и повышение загруженности второго станка на повторной обработке.






 K11 K21
K11 K21





 ст11 ст21
ст11 ст21
Н0 Н1



 K12 K22
K12 K22







 ст12 ст22
ст12 ст22


Схема имитационной модели системы
Для формализации процессов обслуживания в данном цеху используется аппарат Q-схем, так как данные процессы являются, по сути, процессами обслуживания потоков данных.
Одним из основных подходов, используемых при построении математических моделей процессов функционирования систем, является непрерывно-стохастический подход. Особенности этого подхода выражаются в использовании в качестве типовых математических схем систем массового обслуживания, называемых Q-схемами.
Схемы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по сути своей являются процессами обслуживания.
Задачи массового обслуживания возникают в тех случаях, когда условия на выполнение роботы поступают в случайные моменты времени, а выполнение этих работ, называемые обслуживанием, осуществляется одним или несколькими обслуживающими устройствами. Длительность выполнения отдельных требований предполагается случайной.
В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки.
Устройство, способное в любой момент времени обслуживать лишь одно требование, называется каналом обслуживания. В данном случае каналами обслуживания являются устройство подготовки данных и два ЭВМ.
Характерной особенностью задач массового обслуживания является возникновение несоответствия между скоростью поступления требований и скоростью обслуживания, в результате чего или оказываются простаивающими обслуживаемые приборы или образуется очередь на обслуживание. Поэтому принципиальный интерес представляют следующие характеристики СМО:
а) длина очереди в различные моменты времени;
б) общая продолжительность нахождения требования в системе обслуживания;
в) доля времени, в течении которого обслуживающие приборы были не заняты.
Для получения математической модели СМО необходимо иметь:
а) описание входящего потока требований;
б) описание способа, каким выполняется обслуживание;
в) описание дисциплины очереди, то есть указание того, каким образом требования поступают из очереди на обслуживание.
Потоком событий называется последовательность событий, которые происходят одна за другой в случайные моменты времени. Однородный поток событий характеризуется только моментами появления этих событий (вызывающими моментами) и задается последовательностью
{tn} = { 0 <= t1 <= t2 <= ... <= ti <= ... },
где ti - момент появления i-ого события - неотрицательное действительное число. Однородный поток может быть задан так же последовательностью отрезков времени между i-ым и (i-1)-ым событием {tn}. В данном случае поток заявок, поступающий на обслуживание в систему (поток партий деталей), является однородным и задается описанным способом.
Поток событий будет называться стационарным, если вероятность появления того или иного числа событий на интервале зависит только от длины этого интервала и не зависит от того, где на оси времени взят этот интервал.
Рассмотрим систему массового обслуживания, на которую поступает регулярный поток требований с заданным интервалом.
Схемы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по сути своей являются процессами обслуживания.
Задачи массового обслуживания возникают в тех случаях, когда условия на выполнение роботы поступают в случайные моменты времени, а выполнение этих работ, называемые обслуживанием, осуществляется одним или несколькими обслуживающими устройствами.
Время обслуживания имеет случайный характер.
В практике моделирования систем для формализации используются не отдельные приборы обслуживания, а композиции многих элементарных приборов обслуживания Пi. Если каналы Кi различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы Пi и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Т.о. для задания Q-схемы необходимо использовать оператор сопряжения R, отражающий взаимосвязь элементов структуры (каналов и накопителей) между собой.
В данной курсовой работе представлена многоканальная Q-схема, которая имеет 3 канала (см. Приложение В): состоит из накопителя Н1, и каналов обслуживания. Входными потоками для этой схемы являются поток деталей, каждая из которых поступает через промежутки времени, заданные со средним значением 50 минут, а также до 12% обрабатываемых деталей возвращаются для повторной обработки. Оператор поведения заявок А: деталь поступает в машинный зал из очереди Н0, если нужный канал обслуживания свободен, иначе становится в очередь (Н0-накопитель с ожиданием); после обслуживания, если первый станок вторичной обработки занят, то становится в очередь, если в накопителе скапливается более трёх заявок, то подключается второй станок вторичной обработки.
Собственными (внутренними) параметрами Q-схемы будут: количество фаз Lф; количество каналов в каждой фазе Lkj, j=1,Lф; ёмкость i-го накопителя Li. Обозначим как подмножество H совокупность собственных параметров Q-схемы:
H = {Lф=2, Lk1 = 2, Lk2 = 2, L1 = 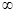 , L2 =
, L2 = 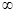 ,}
,}
Т.о. Q-схема, описывающая процесс функционирования системы массового обслуживания любой сложности задаётся в виде:
Q = < W, U, H, Z, R, A > , где
W – подмножество неуправляемых переменных – подмножество входящих потоков заявок на обслуживание;
U – подмножество управляемых переменных – подмножество потоков обслуживания;
R – оператор сопряжения элементов структуры (каналов и накопителей);
H – подмножество собственных параметров (фаз, каналов, накопителей, емкостей);
Z – подмножество состояний элементов структуры (Zi, Zi );
A – оператор алгоритмов обслуживания заявок (оператор поведения заявок).
Большими возможностями обладают имитационные модели, позволяющие обследовать Q-схему, задаваемую без ограничений в виде:
Q = < W , U , H , Z , Y , R , A > ,
где Y - подмножество выходных переменных.
На работу с Q-схемой при машинной реализации моделей ориентированы многие языки имитационного моделирования: SIMULA, SIMSCRIPT, GPSS и др., либо используются пакеты прикладных программ, созданных на базе алгоритмических языков общего назначения ALGOL, FORTRAN, PL/1 и др.
В данной работе рассматривается случай двух каналов, на которые поступают потоки требований с интенсивностью L1, L2. Интенсивность обслуживания равна М.
Среднее число требований, находящихся в системе обслуживания,
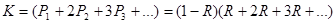 (1.2.1)
(1.2.1)
Учитывая, что
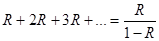 (1.2.2)
(1.2.2)
находим:
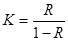 , (1.2.3)
, (1.2.3)
где
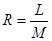 , (1.2.4)
, (1.2.4)
Можно также найти среднее число заявок Кs проходящих обслуживание. Поскольку число заявок, находящихся на обслуживании, равно нулю, если канал свободен, и единице, во всех остальных случаях, то
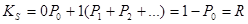 (1.2.5)
(1.2.5)
Разность между К и Кs дает среднюю длину очереди
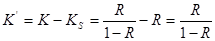 (1.2.6)
(1.2.6)
Учитывая, что среднее время обслуживания одной заявки равно 1/М, для среднего времени ожидания обслуживания получаем выражение:
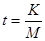 (1.2.7)
(1.2.7)
Еще одним распространенным общим подходом к формальному описанию процессов функционирования систем является подход, предложенный Н.П. Бусленко. Этот подход позволяет описывать поведение непрерывных и дискретных, детерминированных и стохастических систем, т.е. является обобщенным (универсальным) и базируется на понятии агрегативной системы (от англ. aggregate system), представляющий собой формальную схему общего вида, которую будем называть А-схемой. (А-схема программы данного проекта находится в Приложении Г.)
А-схема должна одновременно выполнять несколько функций:
- являться адекватным математическим описанием объекта моделирования, т.е. системы S;
- служить основой для построения алгоритмов и программ при машинной реализации модели M;
- позволять в упрощенном варианте проводить аналитические исследования.
При агрегативном подходе сначала дается формальное определение объекта моделирования – агрегативной системы, которая является математической схемой, отображающей системный характер изучаемых объектов. При агрегативном описании сложный объект (система) разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие. Если некоторые из полученных подсистем оказываются в свою очередь еще достаточно сложными, то процесс их разбиения продолжается до тех пор, пока не образуются подсистемы, которые в условиях рассматриваемой задачи моделирования могут считаться удобными для математического описания. В результате такой декомпозиции сложная система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, объединенных в подсистемы различных уровней.
В качестве элементов А-схемы выступает агрегат, а связь между агрегатами (внутри системы S и с внешней средой E) осуществляется с помощью оператора сопряжения R. Очевидно, что агрегат сам может рассматриваться как А-схема, т.е. может разбиваться на элементы (агрегаты) следующего уровня. Любой агрегат характеризуется следующими множествами: моментов времени Т, входных Х и выходных Y сигналов, состояний Z в каждый момент времени t. Состояние агрегата в момент времени 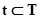 обозначается как
обозначается как 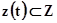 , а входные и выходные сигналы, как
, а входные и выходные сигналы, как 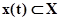 и
и 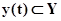 соответственно.
соответственно.
Будем полагать, что переход агрегата из состояния 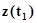 в состояние
в состояние 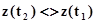 происходит за малый интервал времени, т.е. имеет место скачок. Переходы агрегата из состояний
происходит за малый интервал времени, т.е. имеет место скачок. Переходы агрегата из состояний 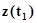 в состояние
в состояние 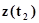 определяются собственными (внутренними) параметрами самого агрегата
определяются собственными (внутренними) параметрами самого агрегата 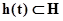 и входными сигналами
и входными сигналами 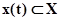 .
.
В начальный момент времени 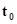 состояния
состояния 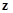 имеют значения равные
имеют значения равные 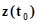 , задаваемые законом распределения процесса
, задаваемые законом распределения процесса 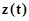 в момент времени
в момент времени 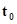 , а именно
, а именно 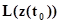 . Предположим, что процесс функционирования агрегата в случае воздействия входного сигнала
. Предположим, что процесс функционирования агрегата в случае воздействия входного сигнала 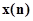 описывается случайным оператором
описывается случайным оператором 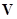 . Тогда в момент поступления в агрегат
. Тогда в момент поступления в агрегат 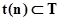 входного сигнала
входного сигнала 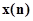 можно определить состояние
можно определить состояние
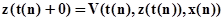 (1.2.8)
(1.2.8)
Обозначим полуинтервал времени 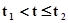 как
как 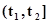 , а полуинтервал
, а полуинтервал 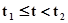 как
как 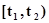 . Если интервал времени
. Если интервал времени 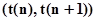 не содержит ни одного момента поступления сигналов, то для
не содержит ни одного момента поступления сигналов, то для 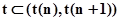 состояние агрегата определяется случайным оператором
состояние агрегата определяется случайным оператором 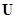 в соответствии с соотношением
в соответствии с соотношением
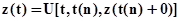 (1.2.9)
(1.2.9)
Совокупность случайных операторов 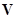 и
и 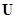 рассматривается как оператор переходов агрегата в новые состояния. При этом процесс функционирования агрегата состоит из скачков состояний в моменты поступления входных сигналов
рассматривается как оператор переходов агрегата в новые состояния. При этом процесс функционирования агрегата состоит из скачков состояний в моменты поступления входных сигналов 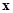 (оператор
(оператор 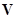 ) и изменений состояний между этими моментами
) и изменений состояний между этими моментами 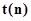 и
и 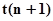 (оператор
(оператор 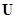 ).
).
Последовательность входных сигналов, расположенных порядке их поступления в А-схему, будем называть входным сообщением или x-сообщением. Последовательность выходных сигналов, упорядоченную относительно времени выдачи, назовем выходным сообщением или y-сообщением.
Ряд предположений о закономерностях функционирования А-схем:
1) взаимодействие между А-схемой и внешней средой Е, а также между отдельными агрегатами внутри системы S осуществляется при передаче сигналов, причем взаимные влияния, имеющие место вне механизма обмена сигналами;
2) для описания сигнала достаточно некоторого конечного набора характеристик;
3) элементарные сигналы мгновенно передаются в А-схеме независимо друг от друга по элементарным каналам;
4) к входному контакту любого элемента А-схемы направляются не более чем один элементарный канал, к входному - любое конечное число элементарных каналов при условии, что по входу одного и того же элемента А-схемы направляется не более чем один из упомянутых элементарных каналов.
Взаимодействие А-схемы с внешней средой Е рассматривается как обмен сигналами между внешней средой Е и элементами А-схемы. Внешняя среда – это множество существующих вне системы элементов любой природы, оказывающих влияние на систему или находящихся под ее воздействием в условиях рассматриваемой задачи. В соответствии с этим внешнюю среду Е можно представить в виде фиктивного элемента системы 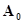 , вход которого содержит
, вход которого содержит 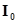 входных контактов, а выход -
входных контактов, а выход - 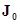 выходных контактов. Сигнал, выдаваемый А-схемой во внешнюю среду Е, принимается элементом
выходных контактов. Сигнал, выдаваемый А-схемой во внешнюю среду Е, принимается элементом 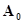 как входной сигнал, состоящий из элементарных сигналов
как входной сигнал, состоящий из элементарных сигналов
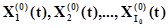 . (1.2.10)
. (1.2.10)
Сигнал, поступающий в А-схему из внешней среды Е, является выходным сигналом элемента 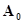 и состоит из элементарных сигналов
и состоит из элементарных сигналов
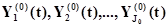 (1.2.11)
(1.2.11)
Таким образом, каждый 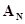 (в том числе и
(в том числе и 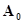 ), как элемент А-схемы в рамках принятых предположений о механизме обмена сигналами достаточно охарактеризовать множеством входных контактов
), как элемент А-схемы в рамках принятых предположений о механизме обмена сигналами достаточно охарактеризовать множеством входных контактов
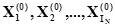 , (1.2.12)
, (1.2.12)
которое обозначим 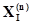 , и множеством выходных контактов
, и множеством выходных контактов
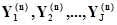 , (1.2.13)
, (1.2.13)
где 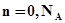 .
.
Полученная пара множеств является математической моделью элемента 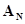 , используемого для формального описания сопряжения его с прочими элементами А-схемы и внешней средой Е.
, используемого для формального описания сопряжения его с прочими элементами А-схемы и внешней средой Е.
Если в А-схеме к контакту 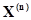 не подключен никакой элементарный канал, то оператор
не подключен никакой элементарный канал, то оператор 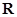 не определен на этом контакте.
не определен на этом контакте.
Оператор 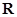 называется оператором сопряжения элементов (агрегатов) в А-схему. Совокупность множеств
называется оператором сопряжения элементов (агрегатов) в А-схему. Совокупность множеств
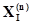 ,
, 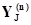 и оператор образуют схему сопряжения элементов в систему S.
и оператор образуют схему сопряжения элементов в систему S.
Оператор сопряжения 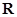 можно задать в виде таблицы, в которой на пересечении строк с номерами элементов (агрегатов)
можно задать в виде таблицы, в которой на пересечении строк с номерами элементов (агрегатов) 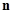 и столбцов с номерами контактов располагаются пары чисел
и столбцов с номерами контактов располагаются пары чисел 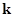 ,
,  , указывающие номер элемента
, указывающие номер элемента 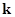 и номер контакта
и номер контакта  , с которым соединен контакт
, с которым соединен контакт 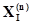 .
.
Если столбцы и строки такой таблицы пронумеровать двойными индексами 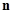 ,
, 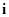 и
и 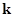 ,
,  соответственно и на пересечении помещать
соответственно и на пересечении помещать 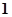 для контактов
для контактов 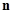 ,
, 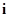 и
и 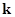 ,
,  , соединенных элементарным каналом и
, соединенных элементарным каналом и 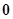 в противном случае, то получим матрицу смежности ориентированного графа, вершинами которого является контакты агрегатов, а дугами - элементарные каналы А-схемы.
в противном случае, то получим матрицу смежности ориентированного графа, вершинами которого является контакты агрегатов, а дугами - элементарные каналы А-схемы.
Рассмотренная схема сопряжения в А-схему, заданная совокупностью множеств и оператором R, является одноуровневой схемой сопряжения.
Обобщенный подход к моделированию сложных систем базируется на агрегативных системах - А-схемах.
Элементом А-схемы является агрегат. Агрегат задается упорядоченной совокупностью:
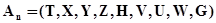
т.е. множествами:
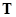 - моментов времени;
- моментов времени;
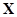 - входных сигналов;
- входных сигналов;
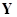 - выходных сигналов;
- выходных сигналов;
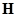 - собственных параметров;
- собственных параметров;
и операторами:
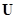 и
и 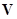 - перехода агрегата в новое состояние;
- перехода агрегата в новое состояние;
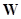 - скачков состояний;
- скачков состояний;
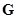 - выдачи выходного сигнала.
- выдачи выходного сигнала.
В одноуровневой схеме сопряжения функционирование сложной системы - это переработка информации: внешней, поступающей извне от источников, не входящих в систему; внутренней, вырабатываемой агрегатами схемы. Агрегаты схемы - это полюса, через которые происходит обмен информацией.
Каждый агрегат 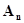 , где
, где 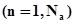 А-схемы имеет входные контакты, на которые поступают сигналы
А-схемы имеет входные контакты, на которые поступают сигналы 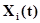 ,
, 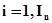 и выходные контакты, с которых снимаются сигналы
и выходные контакты, с которых снимаются сигналы 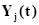 ,
, 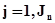 . Под агрегатом
. Под агрегатом 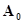 подразумевается воздействие внешней среды.
подразумевается воздействие внешней среды.
ОПИСАHИЕ ПРОГРАММЫ.
Входные и выходные данные.
К входным данным относятся данные, которые могут изменяться пользователем – время обработки заявок на каждом станке, максимально возможный процент брака и общая скорость моделирования.
К выходным данным следует отнести информацию, выводимую в процессе функционирования процесса моделирования:
- общее количество заявок;
- количество заявок, возвращённых на повторную обработку(первичный брак);
- количество деталей, которые попали в разряд бракованных дважды.
Следует отметить, что выполнение данной программы возможно лишь в случае наличия на компьютере всех необходимых технических средств.
2.5. Контрольный пример.
Для времени моделирования, равному поступлению 500 заявок, состояние системы (все параметры – по умолчанию):
- общее количество заявок – 500;
- количество деталей, возвращённых на повторную обработку – 31;
- количество бракованных деталей – 3.
Инструкция пользователю.
Работа с программой не представляет особой сложности даже для пользователя, не имеющего большого опыта работы с персональным компьютером. После запуска программы на экране появляется главное окно программы.
ТЕКСТ ПРОГРАММЫ.
Модуль 1.
unit Progr1;
Interface
uses Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs, ComCtrls, ExtCtrls, StdCtrls, Spin, Menus;
Type
TForm1 = class(TForm)
P1_4: TPanel;
P2_4: TPanel;
P2_3: TPanel;
P1_3: TPanel;
P1_1: TPanel;
pb1: TProgressBar;
pb2: TProgressBar;
Panel8: TPanel;
Panel9: TPanel;
Panel10: TPanel;
Panel11: TPanel;
pb3: TProgressBar;
Panel14: TPanel;
pb4: TProgressBar;
Panel15: TPanel;
Panel16: TPanel;
Panel17: TPanel;
Panel18: TPanel;
Memo2: TMemo;
Memo3: TMemo;
Memo4: TMemo;
Memo5: TMemo;
Timer1: TTimer;
pb_start: TProgressBar;
Timer2: TTimer;
P1_2: TPanel;
P2_1: TPanel;
P2_2: TPanel;
Panel5: TPanel;
Panel21: TPanel;
Panel24: TPanel;
Panel25: TPanel;
Panel26: TPanel;
Panel27: TPanel;
Panel28: TPanel;
Panel31: TPanel;
Label1: TLabel;
Label3: TLabel;
Label2: TLabel;
Label4: TLabel;
p1: TPanel;
p2: TPanel;
Panel34: TPanel;
Panel35: TPanel;
Panel36: TPanel;
Panel38: TPanel;
Panel40: TPanel;
Panel41: TPanel;
Panel42: TPanel;
Panel44: TPanel;
Panel45: TPanel;
Panel12: TPanel;
Label5: TLabel;
Label6: TLabel;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
Label10: TLabel;
indicator1: TProgressBar;
indicator2: TProgressBar;
MainMenu1: TMainMenu;
N1: TMenuItem;
N2: TMenuItem;
N3: TMenuItem;
N4: TMenuItem;
Q1: TMenuItem;
N5: TMenuItem;
N6: TMenuItem;
N7: TMenuItem;
N8: TMenuItem;
N9: TMenuItem;
N10: TMenuItem;
N11: TMenuItem;
Label11: TLabel;
Label12: TLabel;
Label13: TLabel;
Label14: TLabel;
Label15: TLabel;
Label16: TLabel;
Label17: TLabel;
Bevel1: TBevel;
Panel1: TPanel;
procedure Timer2Timer(Sender: TObject);
procedure add_new(ad:byte);
procedure FormCreate(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
procedure N2Click(Sender: TObject);
procedure N3Click(Sender: TObject);
procedure N11Click(Sender: TObject);
procedure N9Click(Sender: TObject);
procedure Q1Click(Sender: TObject);
procedure N5Click(Sender: TObject);
procedure N7Click(Sender: TObject);
procedure N10Click(Sender: TObject);
procedure N8Click(Sender: TObject);
private { Private declarations }
public { Public declarations }
end;
Var
Form1: TForm1;
t1,t2:byte;
Ustanov,zapusk,ripit,
zanyat1,zanyat2,zanyat3,zanyat4:boolean;
have1,have2,have_povtor:boolean;
TotalTime,TotalMessages,
LostMessages,RepeatMessages:longint;
brak1,brak2,time1,time2,time3,time4,zadergka:byte;
Implementation
uses Progr2, progr3, Progr4;
{$R *.DFM}
function where_go(w:byte):boolean;
var x:integer;
begin if (w=1)then begin
x:=trunc(random(100));
if (x>brak1)and(RepeatMessages<(5*(brak1+brak2))) then where_go:=true;end;
if (w=2)then begin
x:=trunc(random(100));if (x>brak2)and(RepeatMessages<(5*(brak1+brak2))) then where_go:=true;end;
end;
procedure prov_nak; {процедура проверки пустоты накопителей}
Begin
have1:=false;have2:=false;have_povtor:=FALSE;
if strtoint(form1.label6.caption)>=1 then have1:=true;
if strtoint(form1.label8.caption)>=1 then have2:=true;
if strtoint(form1.label10.caption)>=1 then have_povtor:=true;
end;
procedure Tform1.add_new(ad:byte);
Begin
if ad=1 then begin
label6.caption:=inttostr(strtoint(label6.caption)+1);
indicator1.Position:=strtoint(label6.caption)*10;
End
Else begin
label8.Caption:=inttostr(strtoint(label8.Caption)+1);
indicator2.Position:=strtoint(label8.Caption)+2;
end;
end;
procedure run;
{переводит заявки из приборов в накопители и наоборот}
Begin
If have1 then
If not(zanyat1) then
Begin
form1.pb1.Max:=time1+round(random(80));{время обработки задания}
form1.pb1.Position:=2;
form1.label6.Caption:=inttostr(strtoint(form1.label6.Caption)-1);
form1.indicator1.Position:=strtoint(form1.label6.Caption)*10;
zanyat1:=true;prov_nak;end;
if have_povtor then if not(zanyat2) then
begin form1.pb2.Max:=time2+round(random(80));
form1.pb2.Position:=2; form1.label10.Caption:=inttostr(strtoint(form1.label10.Caption)-1);
zanyat2:=true;ripit:=true;prov_nak;end;
If have1 then
If not(zanyat2) then
Begin
form1.pb2.Max:=time2+round(random(80)); form1.pb2.Position:=2;
form1.label6.Caption:=inttostr(strtoint(form1.label6.Caption)-1);
form1.indicator1.Position:=strtoint(form1.label6.Caption)*10;
zanyat2:=true;
prov_nak; end;
Begin
form1.pb3.Max:=time3+round(random(80)); form1.pb3.Position:=2;
form1.label8.Caption:=inttostr(strtoint(form1.label8.Caption)-1);
form1.indicator2.Position:=form1.indicator2.Position-2;
zanyat3:=true;prov_nak;end;
if (strtoint(form1.label8.caption)>3) and( not(zanyat4)) then
Begin
form1.pb4.Max:=time4+round(random(80)); form1.pb4.Position:=2;
form1.label8.Caption:=inttostr(strtoint(form1.label8.Caption)-1);
form1.indicator2.Position:=form1.indicator2.Position-2;
zanyat4:=true;
prov_nak;
end;
end;
procedure TForm1.Timer2Timer(Sender: TObject);
var t:real;
i:integer;
Begin
if (zapusk)and(TotalMessages<500) then
Begin
If not(ustanov)then
Begin
t1:=5+trunc(random(10));
ustanov:=true;
zapusk:=ustanov;
t2:=0;
End
Else
if t2=t1 then
Begin
t:=0;
for i:=1 to 1000 do
Begin
pb_start.Position:=(pb_start.Position+trunc(t));
t:=t+0.01;
end;
add_new(1);
inc(TotalMessages);{количество всех сообщений пришедших в систему}
pb_start.Position:=0;
t2:=0;
ustanov:=false;
End
else inc(t2);
prov_nak;
end;
end;
procedure TForm1.FormCreate(Sender: TObject);
Begin
randomize;
label1.Caption:='Ждёт';label2.Caption:='Ждёт';
label3.Caption:='Ждёт';label4.Caption:='Ждёт';
zanyat1:=false;zanyat2:=false;zanyat3:=false;
zanyat4:=false;
brak1:=4;brak2:=8;time1:=40;time2:=60;
time3:=100;time4:=100;
end;
procedure TForm1.Timer1Timer(Sender: TObject);
Begin
If zapusk then begin
if pb1.Position=pb1.max then begin
pb1.Position:=0;zanyat1:=false;
label1.Caption:='Ждёт';
if where_go(1)then add_new(2)
Else
if RepeatMessages<((brak1+brak2)*5) then
Begin
label10.Caption:=inttostr(strtoint(label10.Caption)+1);
inc(RepeatMessages);
End
else add_new(2);
end;
if pb2.Position=pb2.max then
Begin
pb2.Position:=0;zanyat2:=false;label2.Caption:='Ждёт';
if where_go(2)then add_new(2)
Else
if (ripit)and(LostMessages<trunc(RepeatMessages*brak2)/100) then
Begin
p1.Color:=clred;p2.Color:=clred;
p1.Color:=$00400040;p2.Color:=$00400040;
ripit:=false;
inc(LostMessages);
End
Else
if RepeatMessages<((brak1+brak2)*5) then
Begin
label10.Caption:=inttostr(strtoint(label10.Caption)+1);
inc(RepeatMessages);
End
else add_new(2);
end;
if pb3.Position=pb3.max then
begin pb3.Position:=0;zanyat3:=false;label3.Caption:='Ждёт';end;
if pb4.Position=pb4.max then
begin pb4.Position:=0;zanyat4:=false;label4.Caption:='Ждёт';end;
if pb1.Position>0 then
begin pb1.Position:=pb1.Position+7;label1.Caption:='Выполняет';end;
if pb2.Position>0 then
begin pb2.Position:=pb2.Position+7;label2.Caption:='Выполняет';end;
if pb3.Position>0 then
begin pb3.Position:=pb3.Position+7;label3.Caption:='Выполняет';end;
if pb4.Position>0 then
begin pb4.Position:=pb4.Position+7;label4.Caption:='Выполняет';end;
run;
label12.Caption:=inttostr(TotalMessages);
label14.Caption:=inttostr(RepeatMessages);
label16.Caption:=inttostr(LostMessages);
end;
label17.Caption:=timetostr(time);
end;
procedure TForm1.N2Click(Sender: TObject);
Begin
zapusk:=true;
n2.enabled:=false;
n3.enabled:=true;
end;
procedure TForm1.N3Click(Sender: TObject);
Begin
zapusk:=false;
n2.enabled:=true;
n3.enabled:=false;
end;
procedure TForm1.N11Click(Sender: TObject);
Begin
n2.Enabled:=true;
TotalMessages:=0;
LostMessages:=0;
RepeatMessages:=0;
label6.Caption:='0';
label8.Caption:='0';
label10.Caption:='0';
indicator1.Position:=0;
indicator2.Position:=0;
pb1.Position:=0;pb2.Position:=0;
pb3.Position:=0;pb4.Position:=0;
have1:=false;have2:=false;ripit:=false;
zanyat1:=false;zanyat2:=false;
zanyat3:=false;zanyat4:=false;
TotalTime:=0;TotalMessages:=0;
randomize;
end;
procedure TForm1.N9Click(Sender: TObject);
var c:integer;
Begin
c:=application.MessageBox(pchar('Вы уверены в том что хотите завершить работу ???'),pchar('Предупреждение'),4);
if c=6 then halt;
end;
procedure TForm1.Q1Click(Sender: TObject);
Begin
form2.PageControl1.ActivePage:=form2.PageControl1.Pages[0] ;
form2.ShowModal;
end;
procedure TForm1.N5Click(Sender: TObject);
Begin
form2.PageControl1.ActivePage:=form2.PageControl1.Pages[1] ;
form2.ShowModal;
end;
procedure TForm1.N7Click(Sender: TObject);
Begin
form3.PageControl1.ActivePage:=form3.PageControl1.Pages[0];
form3.showmodal;
end;
procedure TForm1.N10Click(Sender: TObject);
Begin
form4.showmodal;
end;
procedure TForm1.N8Click(Sender: TObject);
Begin
form3.PageControl1.ActivePage:=form3.PageControl1.Pages[1];
form3.showmodal;
end;
End.
Модуль 2.
unit Progr2;
Interface
Uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,StdCtrls, ExtCtrls, ComCtrls;
Type
TForm2 = class(TForm)
PageControl1: TPageControl;
TabSheet1: TTabSheet;
TabSheet2: TTabSheet;
Image1: TImage;
Image2: TImage;
Button1: TButton;
procedure Button1Click(Sender: TObject);
Private
Public
end;
Var
Form2: TForm2;
Implementation
{$R *.DFM}
procedure TForm2.Button1Click(Sender: TObject);
Begin
form2.Close;
end;
End.
Модуль 3.
unit Progr3;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, ComCtrls;
type
TForm3 = class(TForm)
PageControl1: TPageControl;
TabSheet1: TTabSheet;
TabSheet2: TTabSheet;
Memo1: TMemo;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Button1: TButton;
procedure Button1Click(Sender: TObject);
private
public
end;
var Form3: TForm3;
implementation
{$R *.DFM}
procedure TForm3.Button1Click(Sender: TObject);
begin form3.Close;
end;
End.
АННОТАЦИЯ.
Пояснительная записка данного курсового проекта, тема которого "Моделирование работы цеха", содержит описание назначения и условий применения программы, описание задачи, общие сведения, функциональное назначение, описание логической структуры программы, используемые технические средства, описание вызова и загрузки, входные и выходные данные для программы, контрольный пример, инструкцию пользователю, текст программы, приложения с изображениями A-схемы и Q-схемы, блок-схемы и экранной формы программы, что вместе составляет 42 листа.
Для реализации алгоритма программы данного курсового проекта был выбран язык программирования Delphi версии 6.0. Существует много различных методов и программных средств для создания программного продукта. Среда визуального программирования выбрана с целью быстрого создания удобного и красивого интерфейса. Среда Borland Delphi выбрана потому, что она позволяет создавать достаточно сложные проекты без высокого уровня знаний самой среды. Среда визуального программирования Delphi позволяет создавать удобный и красивый интерфейс, не требуя при этом больших усилий. Такой интерфейс понятен в использовании любому пользователю, даже начинающему. Delphi позволяет использовать в программе рисунки, строить графики, использовать объекты офисных приложений, использовать мультимедийные эффекты.
При написании данного курсового проекта использовались различные литературные источники, которые перечислены в соответствующем разделе.
Данная работа написана в соответствие с данными варианта №2. Варианты заданий указаны в методическом пособии по написанию курсовой работы, указанном в списке использованной литературы под номером 1.
СОДЕРЖАНИЕ.
Введение
1. Описание применения:
1.1. Назначение и условия применения программы
1.2. Описание задачи
2. Описание программы:
2.1. Общие сведения и функциональное назначение.
2.2. Описание логической структуры
2.3. Используемые технические средства, вызов и загрузка
2.4. Входные и выходные данные
2.5. Контрольный пример
2.6. Инструкция пользователю
3. Текст программы:
3.1. Модуль 1.
3.2. Модуль 2
3.3. Модуль 3.
Список использованных источников
Приложение А.
Приложение Б.
Приложение В
Приложение Г
ВВЕДЕНИЕ.
Для того, чтобы приступить к детальному рассмотрению процесса создания программы данного курсового проекта, необходимо вначале рассмотреть основные термины и понятия, использующиеся в данной пояснительной записке. Прежде всего, следует обратить внимание на термин "моделирование". Сегодня, наверное, невозможно найти такую сферу деятельности человека, в которой в той или иной степени не использовались бы методы моделирования. Особенно это относится к сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации.
Методологическая основа моделирования – диалектико-математический метод познания и научного исследования. Все то, на что направлена человеческая деятельность, называется объектом (от лат. objectum – предмет). Выборка методологии направлена на упорядочения получения и обработки информации об объектах, которые существуют вне нашего сознания и взаимодействуют между собой и внешней средой.
Научно-техническое развитие в любой области обычно идет по пути: наблюдение и эксперимент – теоретические исследования – организация производственных процессов.
Аналогией называют суждение о каком-либо частном сходстве двух объектов. Причем такое сходство может быть существенным и несущественным.
Гипотезы и аналогии, отражающие реальный, объективно существующий мир, должны обладать наглядностью или сводиться к удобным для исследования логическим схемам: такие логические схемы, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений, называются моделями. Другими словами, модель (лат. modulus – мера) – это объект-заместитель объекта - оригинала, обеспечивающий изучение некоторых свойств оригинала.
Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называются моделированием: Таким образом, моделирование может быть определено как представление объекта моделью для получения информации об этом объекте путем проведения экспериментов с его моделью. Теория замещения одних объектов (оригиналов) другими объектами (моделями) и исследования свойств объектов на их моделях называется теорией моделирования.
Если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах, то говорят, что модель адекватна объекту. При этом адекватность модели зависит от цели моделирование и принятых критериев.
Модель – это целевое отображение. Следовательно, для разных целей создаются разные модели. Множество моделей делится на типы по целевому признаку:
1. Познавательные (цель теоретическая). Модели являются формой организации представления знаний, средством соединения новых знаний с имеющимися. Познавательные модели приближают модель к реальности.
2. Прагматические (цель практическая). Модели являются средством управления, средством организации практических действий или их результата. Является рабочим представлением цели, носит нормативный характер. Использование этих моделей состоит в том, чтобы при расхождении модели и реальности, изменить реальность так, чтобы приблизить реальность к модели.
Понятие моделирования практически неотделимо от понятия системы. Системой называется совокупность взаимодействующих элементов, обособленная от среды и взаимодействующая с ней как целое образование, имеющее новое свойство, отсутствующее у элементов системы. Наличие у системы нового свойства называется эмерджентностью.
Элемент системы – это объект, выполняющий функции и не разбиваемый далее в рамках задачи.
Цель системы – это субъективный образ (абстрактная модель) несуществующего, но желаемого состояния среды, которое решило бы проблему.
Согласно первому определению системы, система – это средство достижения цели. Система имеет следующие свойства:
1. Целостность: система имеет свойства, не присущие ее элементам.
2. Целенаправленность.
3. Множественность целей: несовпадение цели системы и целей отдельных компонентов.
4. Обособленность от среды.
5. Динамичность.
6. Абстрактный характер описания: исследуемая система, так или иначе, отличается от объекта наблюдения.
7. Принцип причинности. Это свойство присуще динамическим причинам. Отклик системы на некоторое воздействие не может начаться раньше, чем само воздействие.
Система, в которой происходит изменения со временем, называется динамической. Выделяют два вида динамики: функционирование и развитие. Функционирование – это процесс, происходящий в системе, стабильно реализующей фиксированную цель. Развитие – это то, что происходит с системой при изменении ее цели.
Написание данного курсового проекта позволяет закрепить знания, полученные в процессе изучения дисциплины "Основы теории систем и системного анализа". На этом предмете были изучены основные аспекты системного анализа, понятие о моделях и моделировании, понятие о системе, их классификацию, а также рассмотрены типовые математические схемы.
ОПИСАHИЕ ПРИМЕHЕHИЯ.
Назначение и условия применения программы.
Программа "Моделирование работы цеха" представляет собой законченный программный продукт, который предназначен для удобного и, что главное, наглядного моделирования процесса работы станков в цехе. Данная задача по своей сути является системой массового обслуживания (СМО).
Применение данной программы возможно лишь в случае наличия на компьютере всех необходимых технических средств. К выходным данным следует отнести информацию, выводимую в процессе моделирования, а именно: общее количество поступивших деталей, количество деталей, которые отправлены на повторную обработку, количество отбракованных деталей.Выполнение данной программы производилось при помощи средств диалекта языка программирования Delphi версии 6.0.
Требования программы: персональный компьютер на базе микропроцессора Intel 80586 и выше, VGA совместимая видеокарта, накопитель твёрдом магнитном диске.
Требования к операционной системе ограничены требованиями компилятора языка Delphi 6.0,то есть Windows 98 или выше.
Данная программа довольно наглядно показывает все основные внутренние параметры и состояния данной СМО.
Исходный текст программы находится в нескольких файлах под именем kurs.s и занимает 15 килобайт, а исполняемый модуль под именем Kurs.exe - 228 килобайт.
Описание задачи.
На обрабатывающий участок цеха поступают детали в среднем через 50 мин. Первичная обработка производится на одном из двух станков. Первый станок обрабатывает деталь в среднем 40 мин. и имеет до 4% брака, а второй станок обрабатывает деталь в среднем 60 мин. и имеет до 8% брака. Все детали возвращаются на повторную обработку на второй станок. Детали, который попали в разряд бракованных дважды, считаются отходами. Повторную обработку производят также два станка в среднем 100 мин. каждый. При этом первый станок обрабатывает присутствующие в накопителе после первичной обработки детали, а второй станок подключается при создании в накопителе очереди более трёх деталей. Все интервалы времени распределены по экспоненциальному закону.
Необходимо смоделировать обработку на участке 500 деталей, а также определить загруженность второго станка на повторной обработке и возможность появления отходов, определить возможность уменьшения очереди в накопителе и повышение загруженности второго станка на повторной обработке.



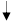



 K11 K21
K11 K21





 ст11 ст21
ст11 ст21
Н0 Н1



 K12 K22
K12 K22







 ст12 ст22
ст12 ст22


Схема имитационной модели системы
Для формализации процессов обслуживания в данном цеху используется аппарат Q-схем, так как данные процессы являются, по сути, процессами обслуживания потоков данных.
Одним из основных подходов, используемых при построении математических моделей процессов функционирования систем, является непрерывно-стохастический подход. Особенности этого подхода выражаются в использовании в качестве типовых математических схем систем массового обслуживания, называемых Q-схемами.
Схемы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по сути своей являются процессами обслуживания.
Задачи массового обслуживания возникают в тех случаях, когда условия на выполнение роботы поступают в случайные моменты времени, а выполнение этих работ, называемые обслуживанием, осуществляется одним или несколькими обслуживающими устройствами. Длительность выполнения отдельных требований предполагается случайной.
В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки.
Устройство, способное в любой момент времени обслуживать лишь одно требование, называется каналом обслуживания. В данном случае каналами обслуживания являются устройство подготовки данных и два ЭВМ.
Характерной особенностью задач массового обслуживания является возникновение несоответствия между скоростью поступления требований и скоростью обслуживания, в результате чего или оказываются простаивающими обслуживаемые приборы или образуется очередь на обслуживание. Поэтому принципиальный интерес представляют следующие характеристики СМО:
а) длина очереди в различные моменты времени;
б) общая продолжительность нахождения требования в системе обслуживания;
в) доля времени, в течении которого обслуживающие приборы были не заняты.
Для получения математической модели СМО необходимо иметь:
а) описание входящего потока требований;
б) описание способа, каким выполняется обслуживание;
в) описание дисциплины очереди, то есть указание того, каким образом требования поступают из очереди на обслуживание.
Потоком событий называется последовательность событий, которые происходят одна за другой в случайные моменты времени. Однородный поток событий характеризуется только моментами появления этих событий (вызывающими моментами) и задается последовательностью
{tn} = { 0 <= t1 <= t2 <= ... <= ti <= ... },
где ti - момент появления i-ого события - неотрицательное действительное число. Однородный поток может быть задан так же последовательностью отрезков времени между i-ым и (i-1)-ым событием {tn}. В данном случае поток заявок, поступающий на обслуживание в систему (поток партий деталей), является однородным и задается описанным способом.
Поток событий будет называться стационарным, если вероятность появления того или иного числа событий на интервале зависит только от длины этого интервала и не зависит от того, где на оси времени взят этот интервал.
Рассмотрим систему массового обслуживания, на которую поступает регулярный поток требований с заданным интервалом.
Схемы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по сути своей являются процессами обслуживания.
Задачи массового обслуживания возникают в тех случаях, когда условия на выполнение роботы поступают в случайные моменты времени, а выполнение этих работ, называемые обслуживанием, осуществляется одним или несколькими обслуживающими устройствами.
Время обслуживания имеет случайный характер.
В практике моделирования систем для формализации используются не отдельные приборы обслуживания, а композиции многих элементарных приборов обслуживания Пi. Если каналы Кi различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы Пi и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Т.о. для задания Q-схемы необходимо использовать оператор сопряжения R, отражающий взаимосвязь элементов структуры (каналов и накопителей) между собой.
В данной курсовой работе представлена многоканальная Q-схема, которая имеет 3 канала (см. Приложение В): состоит из накопителя Н1, и каналов обслуживания. Входными потоками для этой схемы являются поток деталей, каждая из которых поступает через промежутки времени, заданные со средним значением 50 минут, а также до 12% обрабатываемых деталей возвращаются для повторной обработки. Оператор поведения заявок А: деталь поступает в машинный зал из очереди Н0, если нужный канал обслуживания свободен, иначе становится в очередь (Н0-накопитель с ожиданием); после обслуживания, если первый станок вторичной обработки занят, то становится в очередь, если в накопителе скапливается более трёх заявок, то подключается второй станок вторичной обработки.
Собственными (внутренними) параметрами Q-схемы будут: количество фаз Lф; количество каналов в каждой фазе Lkj, j=1,Lф; ёмкость i-го накопителя Li. Обозначим как подмножество H совокупность собственных параметров Q-схемы:
H = {Lф=2, Lk1 = 2, Lk2 = 2, L1 = 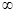 , L2 =
, L2 = 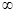 ,}
,}
Т.о. Q-схема, описывающая процесс функционирования системы массового обслуживания любой сложности задаётся в виде:
Q = < W, U, H, Z, R, A > , где
W – подмножество неуправляемых переменных – подмножество входящих потоков заявок на обслуживание;
U – подмножество управляемых переменных – подмножество потоков обслуживания;
R – оператор сопряжения элементов структуры (каналов и накопителей);
H – подмножество собственных параметров (фаз, каналов, накопителей, емкостей);
Z – подмножество состояний элементов структуры (Zi, Zi );
A – оператор алгоритмов обслуживания заявок (оператор поведения заявок).
Большими возможностями обладают имитационные модели, позволяющие обследовать Q-схему, задаваемую без ограничений в виде:
Q = < W , U , H , Z , Y , R , A > ,
где Y - подмножество выходных переменных.
На работу с Q-схемой при машинной реализации моделей ориентированы многие языки имитационного моделирования: SIMULA, SIMSCRIPT, GPSS и др., либо используются пакеты прикладных программ, созданных на базе алгоритмических языков общего назначения ALGOL, FORTRAN, PL/1 и др.
В данной работе рассматривается случай двух каналов, на которые поступают потоки требований с интенсивностью L1, L2. Интенсивность обслуживания равна М.
Среднее число требований, находящихся в системе обслуживания,
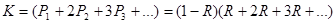 (1.2.1)
(1.2.1)
Учитывая, что
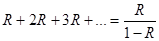 (1.2.2)
(1.2.2)
находим:
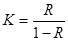 , (1.2.3)
, (1.2.3)
где
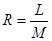 , (1.2.4)
, (1.2.4)
Можно также найти среднее число заявок Кs проходящих обслуживание. Поскольку число заявок, находящихся на обслуживании, равно нулю, если канал свободен, и единице, во всех остальных случаях, то
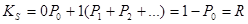 (1.2.5)
(1.2.5)
Разность между К и Кs дает среднюю длину очереди
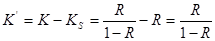 (1.2.6)
(1.2.6)
Учитывая, что среднее время обслуживания одной заявки равно 1/М, для среднего времени ожидания обслуживания получаем выражение:
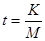 (1.2.7)
(1.2.7)
Еще одним распространенным общим подходом к формальному описанию процессов функционирования систем является подход, предложенный Н.П. Бусленко. Этот подход позволяет описывать поведение непрерывных и дискретных, детерминированных и стохастических систем, т.е. является обобщенным (универсальным) и базируется на понятии агрегативной системы (от англ. aggregate system), представляющий собой формальную схему общего вида, которую будем называть А-схемой. (А-схема программы данного проекта находится в Приложении Г.)
А-схема должна одновременно выполнять несколько функций:
- являться адекватным математическим описанием объекта моделирования, т.е. системы S;
- служить основой для построения алгоритмов и программ при машинной реализации модели M;
- позволять в упрощенном варианте проводить аналитические исследования.
При агрегативном подходе сначала дается формальное определение объекта моделирования – агрегативной системы, которая является математической схемой, отображающей системный характер изучаемых объектов. При агрегативном описании сложный объект (система) разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие. Если некоторые из полученных подсистем оказываются в свою очередь еще достаточно сложными, то процесс их разбиения продолжается до тех пор, пока не образуются подсистемы, которые в условиях рассматриваемой задачи моделирования могут считаться удобными для математического описания. В результате такой декомпозиции сложная система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, объединенных в подсистемы различных уровней.
В качестве элементов А-схемы выступает агрегат, а связь между агрегатами (внутри системы S и с внешней средой E) осуществляется с помощью оператора сопряжения R. Очевидно, что агрегат сам может рассматриваться как А-схема, т.е. может разбиваться на элементы (агрегаты) следующего уровня. Любой агрегат характеризуется следующими множествами: моментов времени Т, входных Х и выходных Y сигналов, состояний Z в каждый момент времени t. Состояние агрегата в момент времени 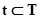 обозначается как
обозначается как 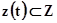 , а входные и выходные сигналы, как
, а входные и выходные сигналы, как 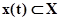 и
и 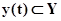 соответственно.
соответственно.
Будем полагать, что переход агрегата из состояния 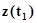 в состояние
в состояние 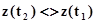 происходит за малый интервал времени, т.е. имеет место скачок. Переходы агрегата из состояний
происходит за малый интервал времени, т.е. имеет место скачок. Переходы агрегата из состояний 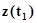 в состояние
в состояние 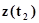 определяются собственными (внутренними) параметрами самого агрегата
определяются собственными (внутренними) параметрами самого агрегата 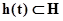 и входными сигналами
и входными сигналами 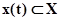 .
.
В начальный момент времени 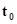 состояния
состояния 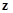 имеют значения равные
имеют значения равные 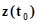 , задаваемые законом распределения процесса
, задаваемые законом распределения процесса 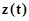 в момент времени
в момент времени 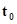 , а именно
, а именно 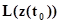 . Предположим, что процесс функционирования агрегата в случае воздействия входного сигнала
. Предположим, что процесс функционирования агрегата в случае воздействия входного сигнала 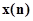 описывается случайным оператором
описывается случайным оператором 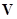 . Тогда в момент поступления в агрегат
. Тогда в момент поступления в агрегат 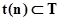 входного сигнала
входного сигнала 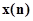 можно определить состояние
можно определить состояние
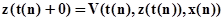 (1.2.8)
(1.2.8)
Обозначим полуинтервал времени 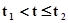 как
как 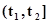 , а полуинтервал
, а полуинтервал 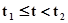 как
как 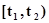 . Если интервал времени
. Если интервал времени 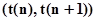 не содержит ни одного момента поступления сигналов, то для
не содержит ни одного момента поступления сигналов, то для 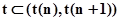 состояние агрегата определяется случайным оператором
состояние агрегата определяется случайным оператором 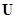 в соответствии с соотношением
в соответствии с соотношением
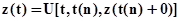 (1.2.9)
(1.2.9)
Совокупность случайных операторов 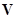 и
и 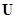 рассматривается как оператор переходов агрегата в новые состояния. При этом процесс функционирования агрегата состоит из скачков состояний в моменты поступления входных сигналов
рассматривается как оператор переходов агрегата в новые состояния. При этом процесс функционирования агрегата состоит из скачков состояний в моменты поступления входных сигналов 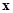 (оператор
(оператор 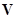 ) и изменений состояний между этими моментами
) и изменений состояний между этими моментами 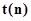 и
и 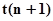 (оператор
(оператор 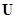 ).
).
Последовательность входных сигналов, расположенных порядке их поступления в А-схему, будем называть входным сообщением или x-сообщением. Последовательность выходных сигналов, упорядоченную относительно времени выдачи, назовем выходным сообщением или y-сообщением.
Ряд предположений о закономерностях функционирования А-схем:
1) взаимодействие между А-схемой и внешней средой Е, а также между отдельными агрегатами внутри системы S осуществляется при передаче сигналов, причем взаимные влияния, имеющие место вне механизма обмена сигналами;
2) для описания сигнала достаточно некоторого конечного набора характеристик;
3) элементарные сигналы мгновенно передаются в А-схеме независимо друг от друга по элементарным каналам;
4) к входному контакту любого элемента А-схемы направляются не более чем один элементарный канал, к входному - любое конечное число элементарных каналов при условии, что по входу одного и того же элемента А-схемы направляется не более чем один из упомянутых элементарных каналов.
Взаимодействие А-схемы с внешней средой Е рассматривается как обмен сигналами между внешней средой Е и элементами А-схемы. Внешняя среда – это множество существующих вне системы элементов любой природы, оказывающих влияние на систему или находящихся под ее воздействием в условиях рассматриваемой задачи. В соответствии с этим внешнюю среду Е можно представить в виде фиктивного элемента системы 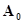 , вход которого содержит
, вход которого содержит 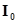 входных контактов, а выход -
входных контактов, а выход - 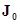 выходных контактов. Сигнал, выдаваемый А-схемой во внешнюю среду Е, принимается элементом
выходных контактов. Сигнал, выдаваемый А-схемой во внешнюю среду Е, принимается элементом 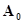 как входной сигнал, состоящий из элементарных сигналов
как входной сигнал, состоящий из элементарных сигналов
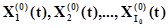 . (1.2.10)
. (1.2.10)
Сигнал, поступающий в А-схему из внешней среды Е, является выходным сигналом элемента 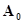 и состоит из элементарных сигналов
и состоит из элементарных сигналов
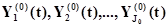 (1.2.11)
(1.2.11)
Таким образом, каждый 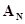 (в том числе и
(в том числе и 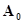 ), как элемент А-схемы в рамках принятых предположений о механизме обмена сигналами достаточно охарактеризовать множеством входных контактов
), как элемент А-схемы в рамках принятых предположений о механизме обмена сигналами достаточно охарактеризовать множеством входных контактов
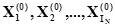 , (1.2.12)
, (1.2.12)
которое обозначим 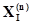 , и множеством выходных контактов
, и множеством выходных контактов
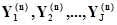 , (1.2.13)
, (1.2.13)
где 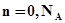 .
.
Полученная пара множеств является математической моделью элемента 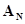 , используемого для формального описания сопряжения его с прочими элементами А-схемы и внешней средой Е.
, используемого для формального описания сопряжения его с прочими элементами А-схемы и внешней средой Е.
Если в А-схеме к контакту 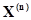 не подключен никакой элементарный канал, то оператор
не подключен никакой элементарный канал, то оператор 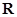 не определен на этом контакте.
не определен на этом контакте.
Оператор 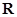 называется оператором сопряжения элементов (агрегатов) в А-схему. Совокупность множеств
называется оператором сопряжения элементов (агрегатов) в А-схему. Совокупность множеств
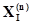 ,
, 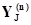 и оператор образуют схему сопряжения элементов в систему S.
и оператор образуют схему сопряжения элементов в систему S.
Оператор сопряжения 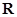 можно задать в виде таблицы, в которой на пересечении строк с номерами элементов (агрегатов)
можно задать в виде таблицы, в которой на пересечении строк с номерами элементов (агрегатов) 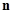 и столбцов с номерами контактов располагаются пары чисел
и столбцов с номерами контактов располагаются пары чисел 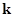 ,
,  , указывающие номер элемента
, указывающие номер элемента 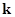 и номер контакта
и номер контакта  , с которым соединен контакт
, с которым соединен контакт 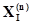 .
.
Если столбцы и строки такой таблицы пронумеровать двойными индексами 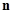 ,
, 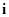 и
и 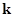 ,
,  соответственно и на пересечении помещать
соответственно и на пересечении помещать 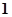 для контактов
для контактов 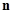 ,
, 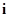 и
и 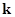 ,
,  , соединенных элементарным каналом и
, соединенных элементарным каналом и 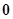 в противном случае, то получим матрицу смежности ориентированного графа, вершинами которого является контакты агрегатов, а дугами - элементарные каналы А-схемы.
в противном случае, то получим матрицу смежности ориентированного графа, вершинами которого является контакты агрегатов, а дугами - элементарные каналы А-схемы.
Рассмотренная схема сопряжения в А-схему, заданная совокупностью множеств и оператором R, является одноуровневой схемой сопряжения.
Обобщенный подход к моделированию сложных систем базируется на агрегативных системах - А-схемах.
Элементом А-схемы является агрегат. Агрегат задается упорядоченной совокупностью:
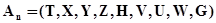
т.е. множествами:
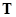 - моментов времени;
- моментов времени;
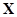 - входных сигналов;
- входных сигналов;
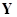 - выходных сигналов;
- выходных сигналов;
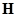 - собственных параметров;
- собственных параметров;
и операторами:
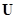 и
и 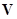 - перехода агрегата в новое состояние;
- перехода агрегата в новое состояние;
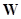 - скачков состояний;
- скачков состояний;
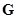 - выдачи выходного сигнала.
- выдачи выходного сигнала.
В одноуровневой схеме сопряжения функционирование сложной системы - это переработка информации: внешней, поступающей извне от источников, не входящих в систему; внутренней, вырабатываемой агрегатами схемы. Агрегаты схемы - это полюса, через которые происходит обмен информацией.
Каждый агрегат 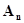 , где
, где 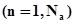 А-схемы имеет входные контакты, на которые поступают сигналы
А-схемы имеет входные контакты, на которые поступают сигналы 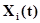 ,
, 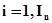 и выходные контакты, с которых снимаются сигналы
и выходные контакты, с которых снимаются сигналы 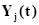 ,
, 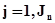 . Под агрегатом
. Под агрегатом 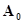 подразумевается воздействие внешней среды.
подразумевается воздействие внешней среды.
ОПИСАHИЕ ПРОГРАММЫ.
Дата: 2019-05-28, просмотров: 285.