В данном пункте анализа надёжности будут рассмотрены вычислители устойчивости ВУ-9 и ВУ-10, так как в системе улучшения устойчивости они имели больше всего отказов.
Наработка до отказа вычислителей ВУ-9 и ВУ-10 образует ряд:
5397, 4066, 3637, 2600, 1062, 9574, 1727, 7295, 5720, 11490, 10957, 8765, 8156, 8575, 7845, 11158, 9120, 5760, 8259, 7071, 8183, 3160, 2121, 3675, 1891, 7497, 8719, 345, 5173, 8873, 8447, 8100.
Выстроим ряд по возрастанию для удобства восприятия и обработки информации:
345, 1062, 1727, 1891, 2121, 2600, 3160, 3637, 3675, 4066, 5173, 5397, 5720, 5760, 7071, 7295, 7497, 7845, 8100, 8156, 8183, 8259, 8447, 8575, 8719, 8765, 8873, 9120, 9574, 10957, 11158, 11490.
Для анализа надёжности определимся с планом наблюдения.
В нашем случае приемлем план наблюдения NUr;
N – число объектов поставленных на испытание;
U – план наблюдения для неремонтируемых объектов;
r – фиксированное число отказов.
Таким образом N=40, r=32
Определяем число интервалов разбиения:
k = 1+3.3∙lg r = 1+3.3∙lg32 = 5
Находим протяжённость интервала:
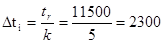
Произведём расчёт эмпирических характеристик, результаты расчёта сведём в таблицу 3:
Таблица 3
| Nинт. | ti-1 | ti | ∆ti | ∆ni | 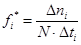
| 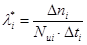
| 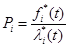
|
| 1 | 0 | 2300 | 2300 | 6 | 6,5217 | 6,5217 | 1 |
| 2 | 2300 | 4600 | 2300 | 7 | 7,6087 | 8,9514 | 0,85 |
| 3 | 4600 | 6900 | 2300 | 8 | 8,6957 | 12,882 | 0,675 |
| 4 | 6900 | 9200 | 2300 | 6 | 6,5217 | 13,73 | 0,475 |
| 5 | 9200 | 11500 | 2300 | 5 | 5,4348 | 16,722 | 0,325 |
На основании полученной таблицы строим графики
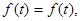
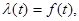
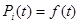
Вычислители ВУ-9 и ВУ-10 являются сложными объектами, состоящими из множества элементов, вероятность отказов которых достаточно мала. Следовательно, можно выдвинуть гипотезу, что отказы вычислителей подчиняются экспоненциальному закону распределения. Этому не противоречит и внешний вид гистограмм.
Определение параметров закона распределения.
Экспоненциальный закон распределения является однопараметрическим, т.е. для его полного определения необходимо найти один параметр — интенсивность отказов л.
Мы осуществили план наблюдения NUr, следовательно, параметр л можно вычислить с использованием метода максимума правдоподобия по формуле:
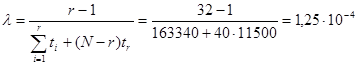 1/ч
1/ч
Отсюда среднее время наработки до отказа
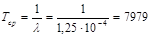 часов.
часов.
Проверка правильности принятой гипотезы.
Осуществляется с помощью критерия Пирсона ч2, рассчитанного по формуле:
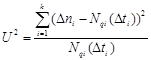
Число разрядов при расчёте критерия на единицу больше числа разрядов разбиения вариационного ряда k, т.к. добавляется интервал от 0 до + ∞. Результаты расчёта представлены в таблице 4:
Таблица 4
| Nинт. | ti-1 час | ti час | ∆ti час | ∆ni шт. | 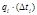
| 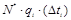
| 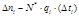
| 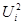
|
| 1 | 0 | 2300 | 2300 | 6 | 0,2504 | 10,017 | -4,017 | 1,611 |
| 2 | 2300 | 4600 | 2300 | 7 | 0,1877 | 7,5084 | -0,508 | 0,034 |
| 3 | 4600 | 6900 | 2300 | 8 | 0,1407 | 5,6281 | 2,3719 | 1 |
| 4 | 6900 | 9200 | 2300 | 6 | 0,1055 | 4,2187 | 1,7813 | 0,752 |
| 5 | 9200 | 11500 | 2300 | 5 | 0,0791 | 3,1623 | 1,8377 | 1,068 |
| 6 | 11500 | 8 | 0,2366 | 9,4656 | -1,466 | 0,227 | ||
| U2= | 4,692 | |||||||
Величина 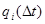 рассчитывается по формуле:
рассчитывается по формуле:
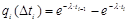
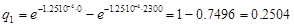
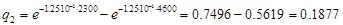
Число степеней свободы r в случае шести разрядов таблицы и одного параметра закона распределения в соответствии с формулой:
r=k-s-1=6-1-1=4, где s — число параметров закона распределения.
Задавшись уровнем значимости 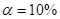 в зависимости от
в зависимости от 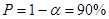 и числа степеней свободы r=4 находим критическое значение
и числа степеней свободы r=4 находим критическое значение 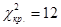 .
.
Подсчитанное значение U2=4,692 не попадает в критическую область (12;+∞), следовательно, принятая гипотеза об экспоненциальном законе распределения не противоречит статистическим данным.
Определение точности оценок параметров распределения.
Верхнюю и нижнюю границы доверительного интервала для параметра л вычисляем по формулам:
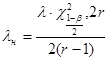 ;
; 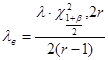
Для доверительной вероятности в=90% и r=32 найдём значения 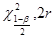 и
и 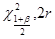 , т.е. значения ч2, соответствующие доверительной вероятности
, т.е. значения ч2, соответствующие доверительной вероятности 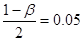 и
и 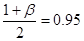 соответственно и числу степеней свободы 2r=2∙32=64
соответственно и числу степеней свободы 2r=2∙32=64
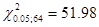 ;
; 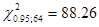
Подставив найденные значения, получим:
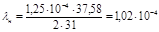
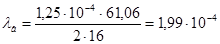
Таким образом, интервал (1,02∙10-4;1,99∙10-4) с доверительной вероятностью 90% покрывает истинное значение параметра л.
Построение графиков распределения.
Построение графиков распределения производим для диапазона 0<t<11500 часов.
Расчётные данные сведены в таблицу 5.
Таблица 5
| t, час | 1150 | 2300 | 3450 | 4600 | 5750 | 6900 | 8050 | 9200 | 10350 | 11500 |
| л( t)∙1 0 - 4 1/ час | 1,25 | 1,25 | 1,25 | 1,25 | 1,25 | 1,25 | 1,25 | 1,25 | 1,25 | 1,25 |
| f(t)∙10- 5 1/ час | 11 | 9,39 | 8,13 | 7,04 | 6,1 | 5,28 | 4,57 | 3,96 | 3,43 | 2,97 |
| Рв( t ) | 0,7952 | 0,6324 | 0,5029 | 0,3999 | 0,3180 | 0,2529 | 0,2011 | 0,1599 | 0,1272 | 0,1011 |
| Р( t ) | 0,8658 | 0,7496 | 0,6489 | 0,5617 | 0,4865 | 0,4212 | 0,3646 | 0,3157 | 0,2733 | 0,2366 |
| Рн( t ) | 0,8889 | 0,7902 | 0,7024 | 0,6244 | 0,5551 | 0,4934 | 0,4386 | 0,3899 | 0,3466 | 0,3081 |
Расчёты велись в соответствии с формулами:
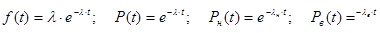
Дата: 2019-05-28, просмотров: 351.