Методы приближённого решения матричных игр
Выполнила студентка V курса
математического факультета
Ветошкина Е. Н.
______________ /подпись/
Научный руководитель:
к. ф.-м. н., доцент, Ковязина Е. М.
______________ /подпись/
Рецензент:
к. ф.-м. н., доцент, Караулов В.М.
______________ /подпись/
Допущена к защите в ГАК
Зав. кафедрой __________________ Вечтомов Е. М.
«___» __________ 2003 г.
Декан факультета _______________ Варанкина В. И.
«___» __________ 2003 г.
Киров
2003
СОДЕРЖАНИЕ
Введение………………………………………………………………………3
§1. Основные понятия………………………………………………………5
§2. Итеративный метод Брауна-Робинсона……………………………...10
§3. Монотонный итеративный алгоритм решения матричных игр…16
Приложение………………………………………………………………….21
Список литературы…………………………………………………………24
Введение
«Теория игр – раздел математики, предметом которого является изучение математических моделей принятия оптимальных решений в условиях конфликта...». [17]
Математическая теория игр способна не только указать оптимальный путь к решению некоторых проблем, но и прогнозировать их исход. Матричные игры серьёзно изучаются специалистами, так как они довольно просты и к ним могут быть сведены игры общего вида. Поэтому теория матричных игр хорошо развита, существуют различные методы поиска решения игр.
Но в большинстве случаев решение матричных игр представляет собой трудный и громоздкий процесс. Есть примеры, когда даже для матриц размера 3´3, процесс поиска решения довольно трудоёмкий.
Кроме того, выигрыши игроков в каждой ситуации не всегда определяются точными измерениями. В процессе сбора данных об изучаемом явлении, анализа этих данных и введения при построении модели различных предположений накапливаются ошибки. Они же могут выражаться числами в матрице выигрышей. Поэтому точность в определении значения игры и оптимальных стратегий игроков оправдана не всегда.
А также, следует заметить, что погрешность в оценке игроком своего выигрыша не может привести к практически серьёзным последствиям и небольшое отклонение игрока от оптимальной стратегии не влечёт за собой существенного изменения в его выигрыше.
Поэтому возникает потребность в разработке численных методов решения матричных игр. В настоящее время в теории игр известны несколько способов приближенного решения матричных игр.
Цель выпускной квалификационной работы изучить некоторые методы приближённого решения матричных игр, обосновать их алгоритмы, и, по возможности, реализовать на языке программирования.
Работа состоит из введения, трёх параграфов и приложения, в котором приведена программа на языке Turbo Pascal, позволяющая находить приближённое решение матричной игры.
В первом параграфе приведены основные понятия и утверждения теории матричных игр.
Параграф второй посвящён изложению приближённого решения игры методом Брауна-Робинсона (метод фиктивного разыгрывания) и его обоснованию. Приведён пример применения алгоритма для конкретной матричной игры.
В третьем параграфе рассмотрен ещё один метод – монотонный итеративный алгоритм приближённого решения матричных игр.
Основные понятия
Будем рассматривать только парные антагонистические игры, т. е. игры в которых участвуют только два игрока – две противоборствующие стороны и выигрыш одного из игроков равен проигрышу другого. Кроме того, будем считать, что каждый игрок имеет лишь конечное число стратегий:
U1={a1, a2,..., am} – множество стратегий первого игрока;
U2={b1, b2, ... bn} – множество стратегий второго игрока.
Будем называть эти стратегии чистыми в отличие от смешанных, которые будут введены далее.
Множество U1×U2 – декартово произведение множеств стратегий игроков называется множеством ситуаций в игре. Для каждой ситуации должен быть определён итог игры. Так как игра антагонистическая достаточно определить выигрыш а одного из игроков, скажем первого. Тогда выигрыш второго игрока будет равен (-а). Таким образом, имеем матрицу выигрышей первого игрока ( для второго игрока матрица выигрышей будет -А):
A= 
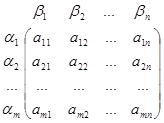
Определение. Система Г={ U 1 , U 2 , A } называется матричной игрой двух лиц.
Разыгрывание матричной игры сводится к выбору игроком 1 i-ой строчки матрицы выигрышей, а игроком 2 - j-го столбца. После этого игрок 1 получает выигрыш равный а ij, а игрок 2 – (-а ij).
При правильной игре игрок 1 может всегда гарантировать себе выигрыш, который назовём нижним значением цены игры. Обозначим его: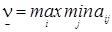 
.
В свою очередь, игрок 2 может гарантировать себе проигрыш, который назовём верхним значением цены игры. Обозначим его:
.
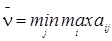Чистые стратегии i* и j*, соответствующие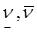 
называются максиминной и минимаксной стратегиями.
Лемма 1. В матричной игре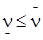 
. [17]
Определение. Ситуация ( i * , j * ) называется ситуацией равновесия, если для i Î 1,2,…, m , j Î 1,2,…, n выполняется неравенство:
.
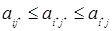Ситуация равновесия это такая ситуация, от которой ни одному из игроков не выгодно отклоняться. В этом случае стратегии i*, j* называют оптимальными стратегиями игроков.
Чтобы такая ситуация существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е.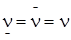 
.[17]
Определение. Пусть( i * , j * ) - ситуацией равновесия в матричной игре. Тогда число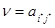 
называется значением или ценой игры.
Например, в игре ГА с матрицей А=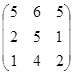 
существует не одна ситуация равновесия. В данной игре их две: (1, 1) и (1, 3).
Множество всех ситуаций равновесия в матричной игре обозначим через Z(Г).
Лемма о масштабе 1. Пусть Г и Г/ - две матричные игры с матрицей выигрышей А={ aij } и A / ={ a / ij }, причём А/= b А+ a , b = const , a = const .
Тогда Z (Г)= Z (Г/) и n / = b n + a (где n / - значение цены игры Г/, n - значение цены игры Г). [17]
Эта лемма имеет большое практическое значение, так как большинство алгоритмов для решения матричных игр основано на предположении, что матрица игры положительна. В случае, когда матрица имеет неположительные элементы, следует прибавить ко всем элементам матрицы число наибольшее по абсолютной величине, из всех отрицательных элементов.
Существуют игры, в которых ситуации равновесия в чистых стратегиях не существует. Тогда игрокам бывает не выгодно придерживаться своих минимаксных и максиминных стратегий, так как они могут получить больший выигрыш, отклонившись от них. В этом случае игрокам разумно действовать случайно, т. е. выбирать стратегии произвольно и не сообщать о выборе сопернику. Такие стратегии игроков будем называть смешанными.
Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.
Так если игрок 1 имеет m чистых стратегий, то его смешанная стратегия x – это набор чисел x =( x 1 , x 2 ,…, xm ), которые удовлетворяют соотношениям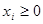 
, 
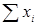=1. Аналогичным образом определяется смешанная стратегия y игрока 2.
Определение. Оптимальными стратегиями игроков называются стратегии, которые при многократном повторении обеспечивают игрокам максимально возможный средний выигрыш (или минимально возможный средний проигрыш).
Таким образом, процесс игры при использовании игроками своих смешанных стратегий превращается в случайное испытание, которое назовём ситуацией в смешанных стратегиях. Она обозначается так ( x , y ), где x и y – смешанные стратегии игроков 1 и 2 соответственно.
Для ситуации в смешанных стратегиях каждый игрок определяет для себя средний выигрыш, который выражается в виде математического ожидания его выигрышей: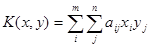 
.
От матричной игры пришли к новой игре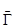 
={X, Y, K}, где X, Y – множества смешанных стратегий игроков, а K – функция выигрышей в смешанных стратегиях. Такую игру называют смешанным расширением матричной игры.
Цели игроков остаются прежними: игрок 1 желает получить максимальный выигрыш, а игрок 2 стремится свести свой проигрыш к минимуму. Поэтому для смешанного расширения игры, аналогичным образом определяются верхнее и нижнее значение цены игры, только теперь игроки выбирают свои смешанные стратегии. Обозначим их:
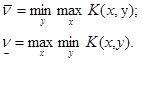
В этом случае остаётся справедливой лемма 1, т. е. .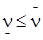
Определение. Ситуация ( x * , y * ) в игре образует ситуацию равновесия, если для всех x Î X , y Î Y выполняется равенство:
K ( x , y * )≤ K ( x * , y * )≤ K ( x * , y ).
Чтобы ситуация равновесия в смешанном расширении игры существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е.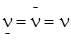 
, где n - цена игры.
Для случая смешанного расширения игры также справедлива лемма о масштабе.
Лемма о масштабе 2.
Пусть ГА и ГА/ - две матричные игры А/= a А+ В, , a = const , В – матрица с одинаковыми элементами b , т. е. b ij = b для всех i , j .
Тогда Z (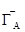 
)= Z (ГА/) и n А / = a n А + b (где n А / - значение цены игры ГА/, n А - значение цены игры ГА). [17]
Теорема. В смешанном расширении матричной игры всегда существует ситуация равновесия. [17]
Var
matr : array [1..10,1..10] of integer ; {Матрица, введенная пользователем}
win_one:array[0..150,1..10] of word; { Массив для выигрышей игр .1}
win_two:array[0..150,1..10] of word; { Массив для выигрышей игр .2}
max,min:integer;
a,i,j,m,n,pl,st,st1,st2,kl:byte;
nol,otr:boolean;
function igr _ one : byte ; {Функция определения следующего}
var a1,a2,max:integer; { хода для игрока 1}
Begin
max:=win_one[a,1];
igr_one:=1;
if pl=1 then a2:=m else a2:=n;
for a1:=1 to a2 do if win_one[a,a1]>max then begin
max:=win_one[a,a1];
igr_one:=a1;
end;
end;
function igr_two:byte; {Функция определения следующего}
var a1,a2,min:integer; { хода для игрока 2}
Begin
min:=win_two[a,1];
igr_two:=1;
if pl=1 then a2:=n else a2:=m;
for a1:=1 to a2 do if win_two[a,a1]<min then begin
min:=win_two[a,a1];
igr_two:=a1;
end;
end;
Begin
clrscr;
End
end else begin {Иначе берем матрицу из константы}
n:=3;m:=3;
for i:=1 to m do for j:=1 to n do matr[i,j]:=matr1[i,j];
end;
clrscr;
Repeat
write(a:2,st:6,' '); {формирование таблицы: номер итерации, стратегия 1игр.}
if pl=2 then begin
for i:=1 to n do begin
win_one[a,i]:=matr[st,i]+win_one[a-1,i]; { формирование матрицы выигрышей 1 игр .}
write(win_one[a,i]:4); { вывод на экран }
end;
st1:=igr_one; {определение ответной стратегии 2 игр.}
gotoxy(32,wherey);
write ( st 1:10,' '); {вывод на экран}
for i:=1 to m do begin
win_two[a,i]:=matr[i,st1]+win_two[a-1,i]; { формирование матрицы выигрышей 2 игр .}
write(win_two[a,i]:4); { вывод на экран }
end;
gotoxy(64,wherey);
write ( win _ one [ a , st 1]:4); {вывод наибольшего суммарного выигрыша 1 игр.}
st:=igr_two; {определение ответной стратегии 1 игр.}
write(win_two[a,st]:4); {вывод наибольшего суммарного выигрыша 2 игр.}
write((win_one[a,st1]+win_two[a,st])/(a*2):6:2); { приближенное значение цены игры }
End
Else
Begin
for i:=1 to m do begin
win_one[a,i]:=matr[i,st]+win_one[a-1,i]; { формирование матрицы выигрышей 1 игр .}
write(win_one[a,i]:4);
end;
st1:=igr_one; {определение ответной стратегии 2 игр.}
gotoxy(32,wherey);
write(st1:10,' ');
for i:=1 to n do begin
win_two[a,i]:=matr[st1,i]+win_two[a-1,i]; { формирование матрицы выигрышей 2 игр .}
write(win_two[a,i]:4);
end;
gotoxy(64,wherey);
write ( win _ one [ a , st 1]:4); {вывод наибольшего суммарного выигрыша 1 игр.}
st:=igr_two; {определение ответной стратегии 1 игр.}
write(win_two[a,st]:4); {вывод наибольшего суммарного выигрыша 2 игр.}
write((win_one[a,st1]+win_two[a,st])/(a*2):6:2); { приближенное значение цены игры }
end;
a:=a+1; {увеличение счетчика итераций}
writeln;
until a=kl+1;
end;
readln;
readln;
End.
Список литературы
1. Беленький В.З. Итеративные методы в теории игр и программировании. М.: «Наука», 1977
2. Блекуэлл Д.А. Теория игр и статистических решений. М., Изд. иностранной литературы, 1958
3. Вентцель Е.С. Элементы теории игр. М., Физматгиз, 1961
4. Вилкас Э.И. Оптимальность в играх и решениях. М.: «Наука», 1986
5. Воробьёв И.Н. Математическая теория игр. М.: «Знание», 1976
6. Давыдов Э.Г. Методы и модели теории антагонистических игр. М.: «Высшая школа», 1990
7. Дрешер М. Стратегические игры. Теория и приложения. М., 1964
8. Исследование операций в экономике / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. М.: «Банки и биржи», Юнити, 1997
9. Итеративный алгоритм решения матричных игр// Доклады Академии наук СССР, том 238, №3, 1978
10. Карлин С. Математические методы в теории игр, программировании и экономике. М.: «Мир», 1964
11. Крапивин В.Ф. Теоретико-игровые методы синтеза сложных систем в конфликтных ситуациях. М.: «Советское радио», 1972
12. Крушевский А.В. Теория игр: [Учебное пособие для вузов]. Киев: «Вища школа», 1977
13. Льюис Р., Райфа Х. Игры и решения. М.,1961
14. Морозов В.В., Старёв А.Г., Фёдоров В.В. Исследование операций в задачах и упражнениях. М.: «Высшая школа», 1996
15. Матричные игры. [Сборник переводов]. Под ред. Воробьёва И.Н. М., Физматгиз, 1961
16. Оуэн Г. Теория игр. [Учебное пособие]. М.: «Мир», 1973
17. Петросян Л.А., Зенкевич Н.А., Семен Е.А. Теория игр. М., 1989
18. Школьная энциклопедия математика. Ред. С. М. Никольский, М.: 1996, с. 380
Методы приближённого решения матричных игр
Выполнила студентка V курса
математического факультета
Ветошкина Е. Н.
______________ /подпись/
Научный руководитель:
к. ф.-м. н., доцент, Ковязина Е. М.
______________ /подпись/
Рецензент:
к. ф.-м. н., доцент, Караулов В.М.
______________ /подпись/
Допущена к защите в ГАК
Зав. кафедрой __________________ Вечтомов Е. М.
«___» __________ 2003 г.
Декан факультета _______________ Варанкина В. И.
«___» __________ 2003 г.
Киров
2003
СОДЕРЖАНИЕ
Введение………………………………………………………………………3
§1. Основные понятия………………………………………………………5
§2. Итеративный метод Брауна-Робинсона……………………………...10
§3. Монотонный итеративный алгоритм решения матричных игр…16
Приложение………………………………………………………………….21
Список литературы…………………………………………………………24
Введение
«Теория игр – раздел математики, предметом которого является изучение математических моделей принятия оптимальных решений в условиях конфликта...». [17]
Математическая теория игр способна не только указать оптимальный путь к решению некоторых проблем, но и прогнозировать их исход. Матричные игры серьёзно изучаются специалистами, так как они довольно просты и к ним могут быть сведены игры общего вида. Поэтому теория матричных игр хорошо развита, существуют различные методы поиска решения игр.
Но в большинстве случаев решение матричных игр представляет собой трудный и громоздкий процесс. Есть примеры, когда даже для матриц размера 3´3, процесс поиска решения довольно трудоёмкий.
Кроме того, выигрыши игроков в каждой ситуации не всегда определяются точными измерениями. В процессе сбора данных об изучаемом явлении, анализа этих данных и введения при построении модели различных предположений накапливаются ошибки. Они же могут выражаться числами в матрице выигрышей. Поэтому точность в определении значения игры и оптимальных стратегий игроков оправдана не всегда.
А также, следует заметить, что погрешность в оценке игроком своего выигрыша не может привести к практически серьёзным последствиям и небольшое отклонение игрока от оптимальной стратегии не влечёт за собой существенного изменения в его выигрыше.
Поэтому возникает потребность в разработке численных методов решения матричных игр. В настоящее время в теории игр известны несколько способов приближенного решения матричных игр.
Цель выпускной квалификационной работы изучить некоторые методы приближённого решения матричных игр, обосновать их алгоритмы, и, по возможности, реализовать на языке программирования.
Работа состоит из введения, трёх параграфов и приложения, в котором приведена программа на языке Turbo Pascal, позволяющая находить приближённое решение матричной игры.
В первом параграфе приведены основные понятия и утверждения теории матричных игр.
Параграф второй посвящён изложению приближённого решения игры методом Брауна-Робинсона (метод фиктивного разыгрывания) и его обоснованию. Приведён пример применения алгоритма для конкретной матричной игры.
В третьем параграфе рассмотрен ещё один метод – монотонный итеративный алгоритм приближённого решения матричных игр.
Основные понятия
Будем рассматривать только парные антагонистические игры, т. е. игры в которых участвуют только два игрока – две противоборствующие стороны и выигрыш одного из игроков равен проигрышу другого. Кроме того, будем считать, что каждый игрок имеет лишь конечное число стратегий:
U1={a1, a2,..., am} – множество стратегий первого игрока;
U2={b1, b2, ... bn} – множество стратегий второго игрока.
Будем называть эти стратегии чистыми в отличие от смешанных, которые будут введены далее.
Множество U1×U2 – декартово произведение множеств стратегий игроков называется множеством ситуаций в игре. Для каждой ситуации должен быть определён итог игры. Так как игра антагонистическая достаточно определить выигрыш а одного из игроков, скажем первого. Тогда выигрыш второго игрока будет равен (-а). Таким образом, имеем матрицу выигрышей первого игрока ( для второго игрока матрица выигрышей будет -А):
A=
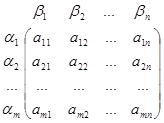
Определение. Система Г={ U 1 , U 2 , A } называется матричной игрой двух лиц.
Разыгрывание матричной игры сводится к выбору игроком 1 i-ой строчки матрицы выигрышей, а игроком 2 - j-го столбца. После этого игрок 1 получает выигрыш равный а ij, а игрок 2 – (-а ij).
При правильной игре игрок 1 может всегда гарантировать себе выигрыш, который назовём нижним значением цены игры. Обозначим его: .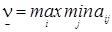
В свою очередь, игрок 2 может гарантировать себе проигрыш, который назовём верхним значением цены игры. Обозначим его:
.
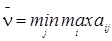Чистые стратегии i* и j*, соответствующие 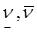называются максиминной и минимаксной стратегиями.
Лемма 1. В матричной игре 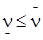. [17]
Определение. Ситуация ( i * , j * ) называется ситуацией равновесия, если для i Î 1,2,…, m , j Î 1,2,…, n выполняется неравенство:
.
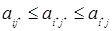Ситуация равновесия это такая ситуация, от которой ни одному из игроков не выгодно отклоняться. В этом случае стратегии i*, j* называют оптимальными стратегиями игроков.
Чтобы такая ситуация существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е. 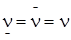.[17]
Определение. Пусть( i * , j * ) - ситуацией равновесия в матричной игре. Тогда число 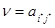называется значением или ценой игры.
Например, в игре ГА с матрицей А= 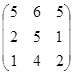существует не одна ситуация равновесия. В данной игре их две: (1, 1) и (1, 3).
Множество всех ситуаций равновесия в матричной игре обозначим через Z(Г).
Лемма о масштабе 1. Пусть Г и Г/ - две матричные игры с матрицей выигрышей А={ aij } и A / ={ a / ij }, причём А/= b А+ a , b = const , a = const .
Тогда Z (Г)= Z (Г/) и n / = b n + a (где n / - значение цены игры Г/, n - значение цены игры Г). [17]
Эта лемма имеет большое практическое значение, так как большинство алгоритмов для решения матричных игр основано на предположении, что матрица игры положительна. В случае, когда матрица имеет неположительные элементы, следует прибавить ко всем элементам матрицы число наибольшее по абсолютной величине, из всех отрицательных элементов.
Существуют игры, в которых ситуации равновесия в чистых стратегиях не существует. Тогда игрокам бывает не выгодно придерживаться своих минимаксных и максиминных стратегий, так как они могут получить больший выигрыш, отклонившись от них. В этом случае игрокам разумно действовать случайно, т. е. выбирать стратегии произвольно и не сообщать о выборе сопернику. Такие стратегии игроков будем называть смешанными.
Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.
Так если игрок 1 имеет m чистых стратегий, то его смешанная стратегия x – это набор чисел x =( x 1 , x 2 ,…, xm ), которые удовлетворяют соотношениям 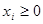, 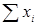=1. Аналогичным образом определяется смешанная стратегия y игрока 2.
Определение. Оптимальными стратегиями игроков называются стратегии, которые при многократном повторении обеспечивают игрокам максимально возможный средний выигрыш (или минимально возможный средний проигрыш).
Таким образом, процесс игры при использовании игроками своих смешанных стратегий превращается в случайное испытание, которое назовём ситуацией в смешанных стратегиях. Она обозначается так ( x , y ), где x и y – смешанные стратегии игроков 1 и 2 соответственно.
Для ситуации в смешанных стратегиях каждый игрок определяет для себя средний выигрыш, который выражается в виде математического ожидания его выигрышей: .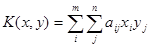
От матричной игры пришли к новой игре 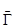={X, Y, K}, где X, Y – множества смешанных стратегий игроков, а K – функция выигрышей в смешанных стратегиях. Такую игру называют смешанным расширением матричной игры.
Цели игроков остаются прежними: игрок 1 желает получить максимальный выигрыш, а игрок 2 стремится свести свой проигрыш к минимуму. Поэтому для смешанного расширения игры, аналогичным образом определяются верхнее и нижнее значение цены игры, только теперь игроки выбирают свои смешанные стратегии. Обозначим их:
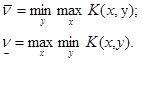
В этом случае остаётся справедливой лемма 1, т. е. .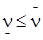
Определение. Ситуация ( x * , y * ) в игре образует ситуацию равновесия, если для всех x Î X , y Î Y выполняется равенство:
K ( x , y * )≤ K ( x * , y * )≤ K ( x * , y ).
Чтобы ситуация равновесия в смешанном расширении игры существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е. 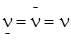, где n - цена игры.
Для случая смешанного расширения игры также справедлива лемма о масштабе.
Лемма о масштабе 2.
Пусть ГА и ГА/ - две матричные игры А/= a А+ В, , a = const , В – матрица с одинаковыми элементами b , т. е. b ij = b для всех i , j .
Тогда Z ( 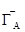)= Z (ГА/) и n А / = a n А + b (где n А / - значение цены игры ГА/, n А - значение цены игры ГА). [17]
Теорема. В смешанном расширении матричной игры всегда существует ситуация равновесия. [17]
Дата: 2019-05-28, просмотров: 175.
