Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Для каскада на операционном усилителе DD 1.4. определили из соотношения 2.1 значения сопротивлений R34, R44, R35 исходя из условия, что коэффициент усиления K_u=10, а сопротивления R34 = R35.

Приняли равными:

R44 = 100 Ом;

R34 = R35 = 1 кОм [14];

Каскад на операционном усилителе DD 4.4 вместе с резисторами R45, R46, R57, R58 является сумматором, складывает выходной сигнал с каскадов на DD 1.4, DD 4.1, DD 4.2, DD 4.3. Для определения значений сопротивлений воспользовались условием равенства R45 = R46 = R57 = R58 и соотношением [13]:

 

1/R52 = 1/R45 + 1/R46 + 1/R57 + R58        (2.2.)

 

Приняли равными:

R45 = R46 = R57 = R58 = 1 кОм;

R52=250 Ом [14];

Значения резисторов R38, R49, R50, R51 приняли равными 10 кОм.

Операционные усилители выбрали TL084ACN (4 в одном корпусе), основные параметры свели в таблицу 2.3 [12].

 

Таблица 2.3. Основные параметры операционного усилителя TL084АСN

№	Название параметра.	Значение и единица измерения
1.	Напряжение питания	± 3,5… ± 18 В
2.	Входной ток	0,05 нА
3.	Коэффициент усиления	70 Дб
4.	Входное сопротивление	1000000 МОм
5.	Тип корпуса	DIP 14

Также для каскадов на DD1.1, DD1.2 и DD 1.3 по формулам 2.1, 2.2 определи значения сопротивлений R1 – R6, R10, R17 – R19, R28 – R29.

Получили значения:

R1 = 3 кОм;

R2 = R4 = R6= R7 = R8 = R9 = R19 = R20 = R31 = 10 кОм;

R3 = R5 = R10 = R21 = R30 = 1 кОм; [14]

Диоды VD1 – VD3 в обвязке драйвера приняли HFA25PB60, (из описания на микросхему IR2135). Значения номиналов конденсаторов С1 – С5 также приведены производителем в документации [2].

Получили значения емкостей конденсаторов:

С1 = С2 = 47 мкФ;

С3 = С4 = С5 = 0,1 мкФ [15];

Для микросхемы Motorola MC3PHAC из документации были взяты номиналы элементов для автономного режима для задания требуемых выходных параметров. Выходная частота инвертора 50 Гц, частота ШИМ 5,3кГц. Микросхема позволяет задавать частоту ШИМ до 20 кГц однако, при ее увеличении значительно возрастают потери в силовых ключах. Выбранные IGBT – транзисторы позволяют работать на заданной (5,3 кГц) частоте, при минимальных потерях на переключение. Частота ШИМ задается напряжением на входе PWMFREQ/FxD [1].

Значения элементов в обвязке микросхемы МС3РНАС:

Резисторы:

R11 = R23 = R24 = R28 = 10 кОм;

R12 – R18 = 56 Ом;

R22 = R26 = R32 = 4,7 кОм;

R27 = R29 = R36 = R41= 1 кОм;

R37 = R40 = R42 = 3 кОм [14];

Конденсаторы:

С6 = С7 = 0,1 мкФ;

С8 = С9 = 0,22 мкФ [15];

Кварцевый генератор НС‑49 с частотой импульсов 4 МГц.

Кнопка без фиксации SB1 – B170H;

Кнопка с фиксацией S1 – PS850L;

Светодиод VD4 – КИПД 24 А-К;

Блок питания системы управления питает микросхемы управления, драйвера, операционные усилители, а также датчики напряжения и тока. Исходя из этого блок питания должен обеспечивать следующие выходные напряжения: ±15 В; +12 В; +5 В. Блок питания разработанный фирмой «Relainse» для питания электроники управления электроприводом подходит для питания элементов системы управления гелеоисточника. Схема электрическая принципиальная показана на рис. 6. Блок питания построен по схеме двухтактного импульсного (ключевого) источника питания. Это современные источники питания с высоким КПД. Традиционные линейные источники питания с последовательным регулирующим элементом сохраняют постоянное выходное напряжение при изменении входного напряжения или тока нагрузки благодаря изменению своего сопротивления. Линейный регулятор(стабилизатор) поэтому может быть очень неэффективным. Импульсный источник питания, однако, использует высокочастотный ключ (транзистор) с переменными величинами включенного-выключенного состояний, чтобы стабилизировать выходное напряжение. Пульсации выходного напряжения, вызванные ключевым режимом, отфильтрованы LC фильтром. Для данного блока питания рассчитали трансформатор TV2, с требуемыми выходными параметрами. Режим работы трансформатора отличается от режима работы, например, в выпрямительных устройствах, силовых цепях синусоидального напряжения. Напряжение, приложенное к первичной обмотке, имеет прямоугольную форму. Расчетные соотношения с учетом основные допущений [8]:

1) скорость перемагничивания сердечника постоянна;

2) дополнительные потери в первичной обмотке, вызванные намагничивающим током, не учитываются;

3) оптимальным является сочетание конструктивных данных, при котором отношение потерь мощности в каждой из обмоток к мощности, передаваемой через нее одинаково;

4) удельное сопротивление обмоток, расположенных вблизи и вдали от зон повышенного нагрева, считается одинаковым.

Исходные данные для расчета:

совокупность чисел, характеризующих фазность обмоток: m₁=2, m₂=3;

напряжение, подключённое к вторичной обмотке: U₂₁=±15 В; U₂₂=5; U₂₃= 12

мощность: P₂=60 Вт;

электродвижущая сила (ЭДС) прикладываемая к первичной обмотке: E1=600 B;

частота коммутаций силовых ключей: f=30 кГц;

температура окружающей среды: То=20 ^оС;

максимально допустимая относительная величина тока намагничивания:

I_{m max}<=0.2;

максимально допустимая температура наиболее нагретой точки трансформатора: T_{т max}=130 ^оС;

коэффициент теплоотдачи: a=1.2×10^-3 Вт/(см² К);

коэффициент полезного действия (КПД): h=0.9.

максимальный коэффициент заполнения окна сердечника обмотки: l_{0 max}=0.7.

Расчёт ориентирован преимущественно на проектирование трансформаторов тороидальной конструкции и состоит из двух частей: оценочного и конструктивного.

Целью оценочного расчета является определение основных параметров трансформатора, выполненного на кольцевом сердечнике разных типоразмеров их стандартного ряда.

Для работы на частоте от 10 кГц и выше в качестве материала сердечника применяются ферриты 2000НМ‑1, 1500НМ‑1 и др. Выбирали марку сердечника. Для этого построили зависимости удельных потерь мощности в сердечнике от перепада индукции DВ в нём:

 

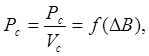                      (2.3)

 

где Р_с - потери мощности в сердечнике, Вт;

V_c - объём сердечника, м³.

Использовали выражение:

 

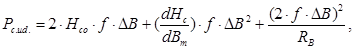 (2.4)

 

где f – заданная частота, кГц;

DВ-изменение магнитной индукции в сердечнике трансформатора за ту часть периода Т/2, когда это изменение происходило в одном направлении, Тл;

H_co, dH_c/dB_m, R_в – величины найденные по таблице 2.4.

По формуле (2.4.) рассчитали для каждого материала зависимость Р_с.уд. от DВ в виде таблицы, задаваясь последовательно значениями:

 

 

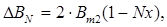
где N – целое число;

х = 0,1.. 0,2;

Bm – амплитудное значение магнитной индукции, Тл (табл. 2.4).

Данные для расчета взяли из таблицы 2.4 [8]:

Таблица 2.4. Параметры аппроксимирующих выражений, описывающих магнитные свойства ряда ферримагнетиков

№ пп	Тип фер.	DB, Тл
		Hco, A/m	dHc/dBm A/(m×Тл)	DH0/dBm, A/(m×Тл)	H0, A/mH0, A/m	Bm2, Тл	b	RВ коМ/м
1.	6000НМ	6.4	0	48.3	776	0.355	15	4.4
2.	4000НМ	1.06	8	80	758	0.38	16	26
3.	3000НМ	3.68	16	94.4	755	0.37	20	31
4.	2000НМ	1.2	40	164	719	0.39	12	56
5.	2000НМ1	7.2	40	160	725	0.34	7	63
6.	1500НМ2	0	65.4	240	699	0.33	10	180
7.	1500НМ3	6.77	37	212	699	0.38	10	180
8.	1000НМ3	20	0	250	715	0.258	10	280
9.	700НМ	0	75.4	844	749	0.4	2	1000

 

Для материала 6000 НМ:

H_co = 6.4 А/м,

dH_c/dB_m = 0 А/(м×Тл),

R_в = 4,4 кОм/м.

x = 0.15

Подставляя числовые значения в (2.3.) получилипри В = 0 Тл

Р_с.уд.=0 Вт/м³

при В=0,1 Тл

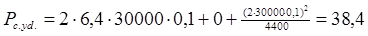
Р_с.уд.= 38,4 Вт/м³,

при В=0,2 Тл

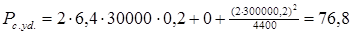
Р_с.уд.= 76,8 Вт/м³, и т.д.

Аналогично рассчитали зависимости Р_с.уд.(В) для других материалов результаты вычислений занесли в таблицу 2.5.

Таблица 2.5. Рассчитанные значения Р_с.уд., Вт/м³.

Тип фер.	DB, Тл
	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7
6000НМ	0	38,4	76,8	115,2	153,7	192,2	230,7	269,2
4000НМ	0	8,7	22,3	40,7	63,8	91,8	124,6	162,2
3000НМ	0	26,8	63,3	109,4	165,1	230,4	305,3	389,8
2000НМ	0	19,2	62,4	129,6	220,8	336,1	475,2	638,4
2000НМ1	0	55,2	134,4	237,6	164,8	516,1	691,2	890,4
1500НМ2	0	19,6	78,5	176,6	313,9	490,5	706,3	961,3
1500НМ3	0	51,7	125,6	221,7	340,1	480,6	643,3	828,2
1000НМ3	0	120	240	360	480	600	720	840
700НМ	0	22,6	90,5	203,6	361,9	565,5	814,3	1108,4

 

По данным таблицы 2.5. построили графики (рис. 2.8).

Анализируя график, увидели, что наименьшими удельными потерями в заданных условиях обладает материал 4000 НМ. Следовательно, выбрали для нашего сердечника материал 4000 НМ.

Определили типоразмеры сердечника в стандартном ряде размеров, начиная с которых сердечники пригодны для изготовления трансформатора с заданными параметрами. При этом мы приняли коэффициент укладки λ₀=0,7. Для этого взяли два любых размера сердечника [9], например К10х6х3 и 2К20х12х6, из стандартного ряда размеров сердечников и нашли для них зависимость Р_{выхмакс} от объёма этих сердечников V_т.

Рассчитали объём V_c кольцевого сердечника [8]:

 

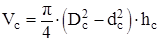; (2.5)

 

где D_c=10∙10^-3 - внешний диаметр кольцевого сердечника К10х6х3, в м;

d_c=6∙10^-3-внутренний диаметр кольцевого сердечника К10х6х3, в м;

h_c=3∙10^-3 - высота кольцевого сердечника К10х6х3, в м;

π=3,14 – константа.

V_c=0,25∙3,14∙(10∙10^-3-6∙10^-3) 3∙10^-3=1.508∙10^-7 м³

Аналогично рассчитали объём сердечника с размерами 2К20х12х6. Полученное значение объёма занесли в таблицу 2.6.

 

Таблица 2.6. Объём выбранного сердечника

Типоразмер сердечника	Искомая величина, м3
К10х6х3	1.508∙10-7
2К20х12х6	2.443∙10-6

 

Определили максимальную мощность потерь на единицу поверхности сердечника [8]:

 

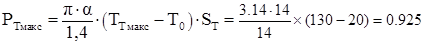, Вт, (2.6)

	Рис 2.8.

где α=14 – коэффициент теплоотдачи, в Вт/(м∙К);

π=3,14 – константа;

Т_Т макс = 130 ‑ максимальная температура трансформатора, в ^oC;

S_T= 3.27∙10^-4 – площадь поверхности сердечника c размерами К10х6х3, берётся из справочника, в м².

Аналогично расчёт произвели для сердечника с размерами 2К20х12х6. Значение максимальной мощности потерь для данного размера сердечника занесли в таблицу 2.7.

 

Таблица 2.7. Максимальная мощность потерь сердечника

Типоразмер сердечника	Искомая величина
К10х6х3	0.925
2К20х12х6	4.891

 

Определили оптимальную магнитную индукцию насыщения ΔB_опт:

 

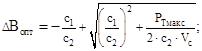 (2.7)

где V_c= 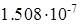- объём сердечника с размерами К10х6х3, в м³;

с₁=f∙H_co=30000∙1,2=3,6∙10⁴;

с₂=30000∙40+(2∙30000)²/56000 = 2,179

R_в=56000 – удельное сопротивление материала 2000 НМ, в Ом.

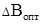=3,6∙10⁴/2,179∙10⁶+((3,6∙10⁴/2,179∙10⁶)+/0,925/2∙2,179∙10⁶∙1,508∙10^-7)^0,5=1,159 Тл

Аналогичный расчёт произвели для сердечника с размерами 2К20х12х6. Значение оптимальной магнитной индукции насыщения ΔB_опт для данного размера сердечника занесли в таблицу 2.8.

 

Таблица 2.8. Оптимальная магнитная индукция насыщения ΔB_опт

Типоразмер сердечника	Искомая величина, Тл
К10х6х3	1,159
2К20х12х6	0,58

 

Из таблицы видно, что ΔB_опт для сердечника К10х6х3 равна 1,159 Тл, что выше максимальной магнитной индукции материала (0,78 Тл), поэтому приняли эту величину равной 0,78 Тл, и дальнейшие расчёты вели для неё.

Нашли потери мощности P_c в сердечнике c размерами К10х6х3:

 

Р_с=Р_с.уд. (ΔB_опт)∙V_c=3.066∙10⁶ ∙1.508∙10^-7=0.462, Дж (2.8)

 

где

Р_с.уд. (ΔB_опт)= 3.066∙10⁶ – удельные потери в магнитопроводе при ΔB=ΔB_опт, в Дж/м³;

V_c=1.508∙10^-7 – объём сердечника с данными размерами, в м³.

Аналогичный расчёт произвели для сердечника с размерами 2К20х12х6. Значение потери мощности потерь P_c в сердечнике для данного размера занесли в таблицу 2.9.

 

Таблица 2.9. Потери мощности P_c в сердечнике

Типоразмер сердечника	Искомая величина, Вт
К10х6х3	1.419∙105
2К20х12х6	8.025∙105

 

Для найденных значений DВ_опт определили амплитудное значение напряжённости магнитного поля Н_m. Для этого использовали данные таблиц 2.4, 2.6 и следующую формулу [8]:

 

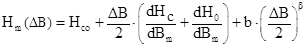, (2.9)

 

DВ=DВ_опт – оптимальная магнитная индукция намагничивания из табл. 2.8

Для сердечника К2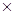0 10 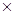5 получили следующий результат:

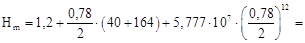796 А/м.

Аналогичный расчёт произвели для сердечника с размерами К10х6х3. Все полученные результаты сведены в таблицу 2.10.

 

Таблица 2.10. Амплитудное значение напряжённости магнитного поля Н_m

Типоразмер сердечника	Искомая величина, А/м
К10х6х3	796,084
2К20х12х6	80,801

 

Рассчитали мощность сердечника с учётом температурной поправки:

 

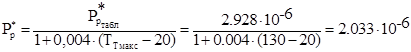, в Вт; (2.10)

 

где 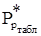= 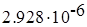Вт/(А∙Гц) – из справочника для сердечника К10х6х3;

Аналогичный расчёт произвели для сердечника с размерами 2К20х12х6. Полученные значения занесли в таблицу 2.11.

 

Таблица 2.11. Мощность сердечника с учётом температурной поправки

Типоразмер сердечника	Искомая величина, Вт
К10х6х3	2.033∙10 -6
2К20х12х6	1,818∙10 -4

 

Нашли величину относительных потерь мощности в обмотках δ [8]:

 

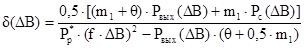 (2.11.)

 

Рассчитанные значения занесли в таблицу 2.12.

 

Таблица 2.12. Величина относительных потерь мощности в обмотках

Типоразмер сердечника	Искомая величина
К10х6х3	0.03
2К20х12х6	6.018∙10 -4

 

Определили относительную величину амплитуды тока намагничивания[8]:

 

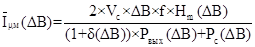,                  (2.12)

 

где d – величина относительных потерь мощности в обмотках, рассчитывается по формуле 2.11;

Р_вых – мощность, которая может быть передана в нагрузку, Вт;

Р_с – потери мощности в сердечнике при данном ΔВ, Вт.

Полученные значения занесли в таблицу 2.13.

 

Таблица 2.13. Относительная величина амплитуды тока намагничивания

Типоразмер сердечника	Искомая величина
К10х6х3	0,151
2К20х12х6	0,182

 

Из справочника нашли объем трансформатора с размерами сердечника К10х6х3 и 2К20х12х6 при λ₀=0,7:

 

Таблица 2.14. Объём трансформатора

Типоразмер сердечника	Искомая величина, см3
К10х6х3	0,56
2К20х12х6	6,85

 

Рассчитали максимальную выходную мощность сердечника с данными размерами:

 

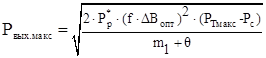 (2.13)

 

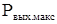= (2·2,033·10⁶·(30000·0,76)²·(0,925–0,462)/2+1)^0,5= 30,8 Вт

Полученные значения занесли в таблицу 2.15.

 

Таблица 2.15. Максимальная мощность даваемая трансформатором в нагрузку

Типоразмер сердечника	Искомая величина, Вт
К10х6х3	30.8
2К20х12х6	499.3

 

По данным таблиц 2.13 и 2.14 построили по двум точкам с координатами (P_{выхмакс}; V_т) зависимость P_{выхмакс} от V_т на рис. 2.9.

По заданной мощности с графика сняли значение объёма трансформатора V_т, V_т=1,2 см³.

Нашли интервал объёмов, в котором может находиться наш сердечник:

V_т.макс= V_т+0.4∙ V_т=1,68 см³; V_т.мин= V_т-0.4V_т=0,72 см³.

По найденному интервалу нашли по справочнику типоразмеры сердечников, объёмы которых лежат в найденном интервале: 2K10x6x3, К12x5x5.5, 2K12x8x3, K16x10x4.5. Из найденных типоразмеров сердечников выбрали наиболее подходящий нашему трансформатору [9].

Используя значения S_т при lо=0.1; 0.3; 0.5; 0.7 для выбранных материалов определили зависимости P_т.макс = f(lо) по формуле 2.6. Результаты вычислений сведены в таблицу 2.16.

 

Таблица 2.16. Значение P_т.макс, Вт

Значение lо	Типоразмер сердечника
	2K10x6x3	К12x5x5.5	2K12x8x3	K16x10x4.5
0.1	0,874	1,151	1,094	1,476
0.3	0,99	1,23	1,295	1,773
0.5	1,105	1,306	1,496	2,067
0.7	1,221	1,385	1,696	2,367

 

Далее пользуясь формулами нашли зависимость P_с=f(DB) для всех выбранных типоразмеров сердечников.

Нашли потери в обмотках, где d находится по формуле 2.11, а P_c определили с учетом формул 2.5 и 2.8 для каждого значения DB и lо.

 

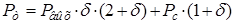              (2.14)

 

Рассчитали потери в трансформаторе для каждого значения d и lо для всех выбранных типоразмеров сердечников по формуле:

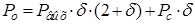   (2.15)

 

Рассчитанные значения P_т, P_o, P_c, d для выбранных типоразмеров сердечников занесены в таблицы 2.17 – 2.20.

 

Таблица 2.17. Значение величин для сердечника 2K10x6x3

Значение lо	Значение DB, Тл	Значения величин
		Рс, Вт	d	Ро, Вт	Рт, Вт
0.1	0,78	0,428	0,066	8,216	8,643
	0,624	0,278	0,108	13,737	14,016
	0,468	0,161	0,217	28,05	29,01
	0,312	0,075	0,761	45	45
	0,156	0,022	1,49	126,23	126,3
0.3	0,78	0,428	0,022	2,696	3,214
	0,624	0,278	0,035	4,298	4,577
	0,468	0,161	0,065	8,026	8,187
	0,312	0,075	0,163	21,166	21,241
	0,156	0,022	1,869	434,053	439,074
0.5	0,78	0,428	0,014	1,692	2,12
	0,624	0,278	0,022	2,674	2,953
	0,468	0,161	0,04	4,897	5,058
	0,312	0,075	0,096	12,108	12,183
	0,156	0,022	0,625	98,427	98,449
0.7	0,78	0,428	0,011	1,285	1,713
	0,624	0,278	0,017	2,024	2,302
	0,468	0,161	0,03	3,677	3,838
	0,312	0,075	0,071	8,873	8,948
	0,156	0,022	0,399	57,445	57,466

 

По данным таблицы для каждого значения l_о построили зависимость P_o(DB), Р_с(DB), Р_т(DB) для l_о=0,1 ‑ рис. 2.10, l_о=0,3 ‑ рис. 2.11, l_о=0,5‑рис. 2.12, l_о=0,7 ‑ рис. 2.13.

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,1.

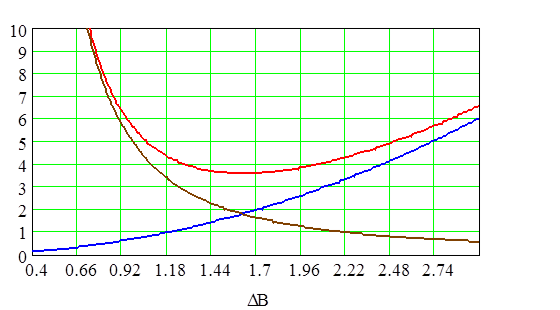
Рис. 2.10

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,3.

 

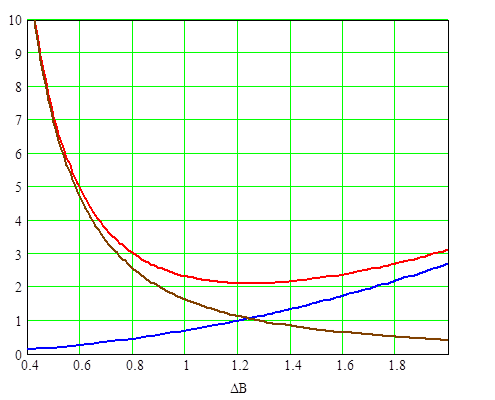
Рис. 2.11

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,5.

 

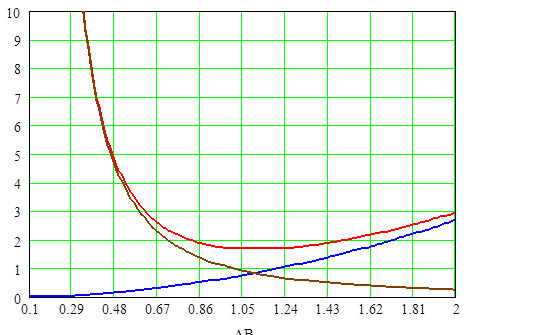
Рис. 2.12

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,7.

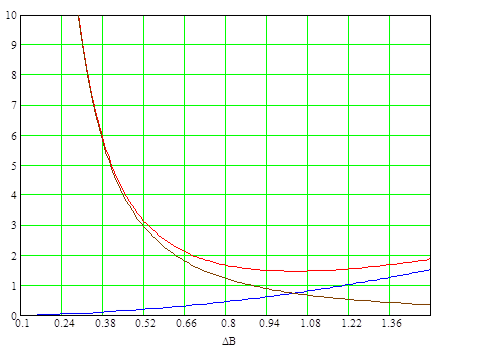
Рис. 2.13.

Таблица 2.18. Значение величин для сердечника 2K12x8x3

Значение lо	Значение DB, Тл	Значения величин
		Рс, Вт	d	Ро, Вт	Рт, Вт
0.1	0,78	0,535	0,036	4,445	4,98
	0,624	0,348	0,058	7,188	7,536
	0,468	0,201	0,11	13,894	14,096
	0,312	0,094	0,301	41,615	41,709
	0,156	0,027	5,9	1389	1389,1
0.3	0,78	0,535	0,013	1,541	2,076
	0,624	0,348	0,02	2,431	2,779
	0,468	0,201	0,036	4,436	4,637
	0,312	0,094	0,087	10,861	10,955
	0,156	0,027	0,53	81,484	80,511
0.5	0,78	0,535	0,008	0,994	1,529
	0,624	0,348	0,013	1,561	1,909
	0,468	0,201	0,023	2,818	3,019
	0,312	0,094	0,054	6,682	6,777
	0,156	0,027	0,276	37,756	37,783
0.7	0,78	0,535	0,006	0,771	1,306
	0,624	0,348	0,009	1,029	1,557
	0,468	0,201	0,018	2,174	2,375
	0,312	0,094	0,042	5,09	5,184
	0,156	0,027	0,199	26,256	26,283

 

По данным таблицы для каждого значения l_о построили зависимость P_o(DB), Р_с(DB), Р_т(DB) для l_о=0,1 ‑ рис. 2.14, l_о=0,3 ‑ рис. 2.15, l_о=0,5 ‑ рис. 2.16, l_о=0,7 ‑ рис. 2.17.

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,1.

 

 

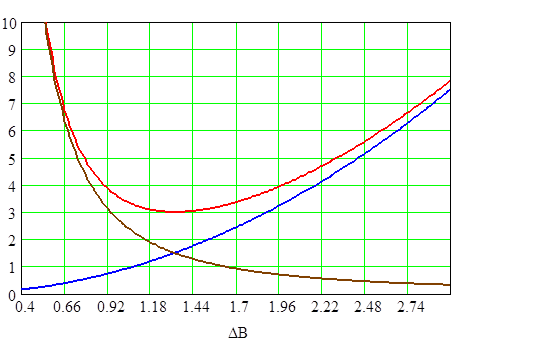
Рис. 2.14.

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,3.

 

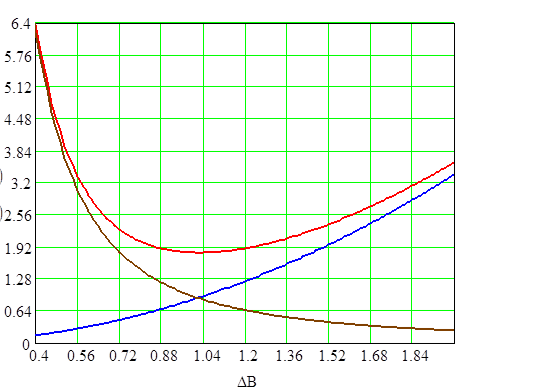
Рис. 2.15.

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,5.

 

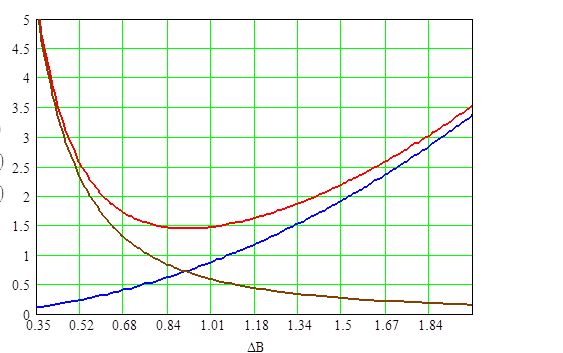
Рис. 2.16

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,7.

 

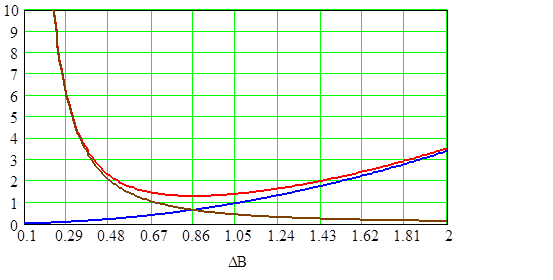
Рис. 2.17

Таблица 2.19. Значение величин для сердечника K12x5x5,5

Значение lо	Значение DB, Тл	Значения величин
		Рс, Вт	d	Ро, Вт	Рт, Вт
0.1	0,78	0,729	0,04	4,928	5,657
	0,624	0,475	0,064	7,991	8,465
	0,468	0,274	0,122	15,58	15,854
	0,312	0,128	0,344	48,437	48,565
	0,156	0,037	3,673	368,472	368,509
0.3	0,78	0,729	0,013	1,63	2,359
	0,624	0,475	0,021	2,569	3,043
	0,468	0,274	0,038	4,69	4,964
	0,312	0,128	0,092	11,532	11,661
	0,156	0,037	0,579	89,64	89,677
0.5	0,78	0,729	0,008	1,011	1,741
	0,624	0,475	0,013	1,586	2,061
	0,468	0,274	0,024	2,862	3,136
	0,312	0,128	0,055	0,786	6,914
	0,156	0,037	0,282	38,548	38,585
0.7	0,78	0,729	0,006	0,756	1,485
	0,624	0,475	0,01	1,182	1,657
	0,468	0,274	0,018	2,123	2,398
	0,312	0,128	0,04	4,963	5,091
	0,156	0,037	0,193	25,407	25,444

 

По данным таблицы для каждого значения l_о построили зависимость P_o(DB), Р_с(DB), Р_т(DB) для l_о=0,1 ‑ рис. 2.18, l_о=0,3 ‑ рис. 2.19, l_о=0,5 ‑ рис. 2.20, l_о=0,7 ‑ рис. 2.21.

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,1 для сердечника К12х5х5,5.

 

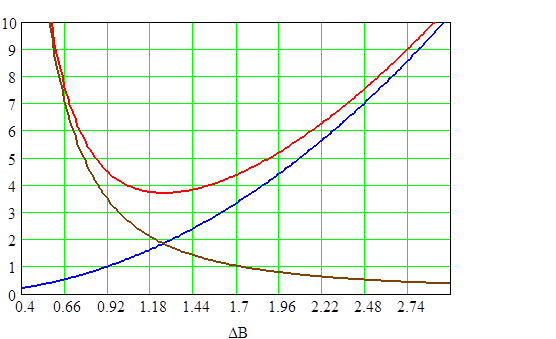
Рис. 2.18.

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,3 для сердечника К12х5х5,5.

 

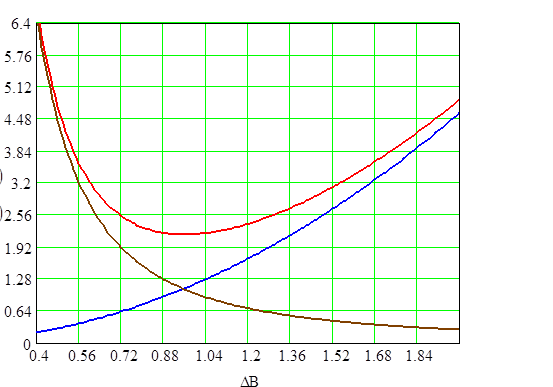
Рис. 2.19

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,5 для сердечника К12х5х5,5.

 

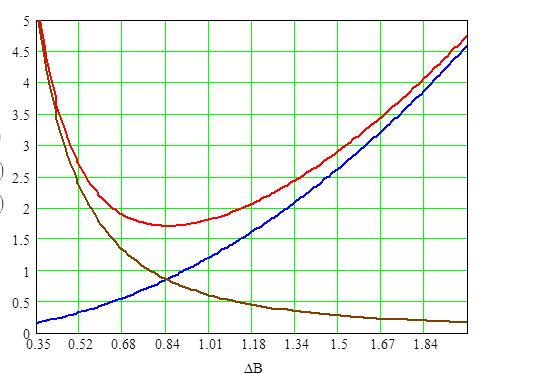
Рис. 2.20

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,7 для сердечника К12х5х5,5.

 

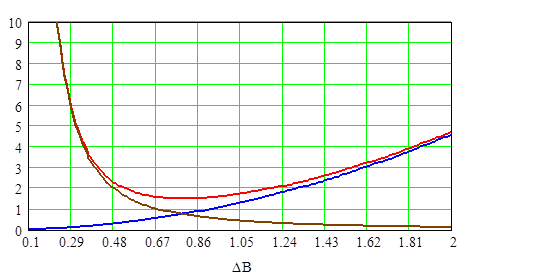
Рис. 2.21

Таблица 2.20. Значение величин для сердечника K16x10x4,5

Значение lо	Значение DB, Тл	Значения величин
		Рс, Вт	d	Ро, Вт	Рт, Вт
0.1	0,78	0,782	0,017	2,07	2,853
	0,624	0,509	0,027	3,275	3,784
	0,468	0,294	0,049	6,028	6,222
	0,312	0,138	0,12	15,225	15,363
	0,156	0,04	0,915	160	160,048
0.3	0,78	0,782	0,006	0,75	1,533
	0,624	0,509	0,001	1,174	1,683
	0,468	0,294	0,017	2,107	2,401
	0,312	0,138	0,04	4,922	5,059
	0,156	0,04	0,191	25,136	25,175
0.5	0,78	0,782	0,004	0,497	1,279
	0,624	0,509	0,006	0,775	1,284
	0,468	0,294	0011	1,385	1,679
	0,312	0,138	0,026	3,19	3,328
	0,156	0,04	0,117	14,826	14,901
0.7	0,78	0,782	0,003	0,394	1,176
	0,624	0,509	0005	0,614	1,123
	0,468	0,294	0,009	1,095	1,389
	0,312	0,138	0,021	2,507	2,645
	0,156	0,04	0,09	11,284	11,324

 

По данным таблицы для каждого значения l_о построили зависимость P_o(DB), Р_с(DB), Р_т(DB) для l_о=0,1 ‑ рис. 2.22, l_о=0,3 ‑ рис. 2.23, l_о=0,5 ‑ рис. 2.24, l_о=0,7 ‑ рис. 2.25.

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,1 для сердечника К16х10х4,5.

 

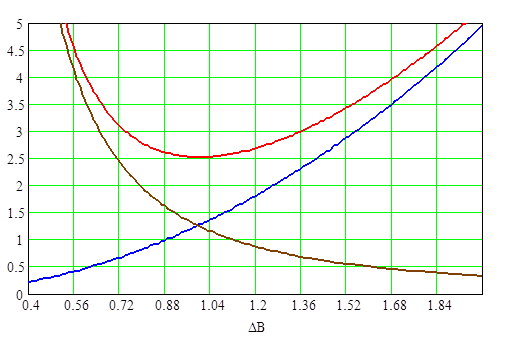
Рис. 2.22

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,3 для сердечника К16х10х4,5.

 

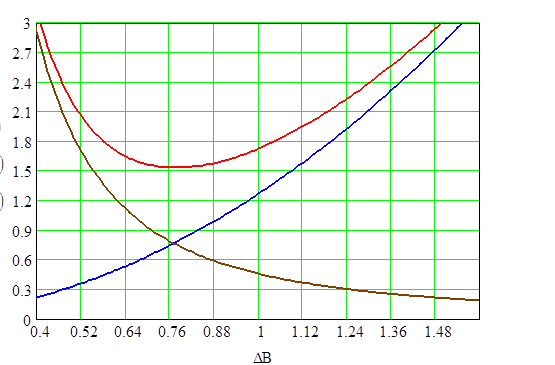
Рис. 2.23

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,5 для сердечника К16х10х4,5.

 

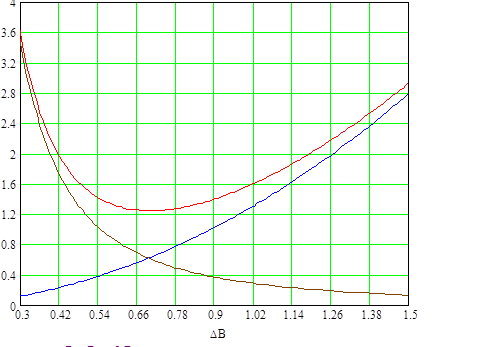
Рис. 2.24

 

Графики зависимости Р_о, Р_с, Р_т от величины магнитной индукции при λ_о=0,7 для сердечника К16х10х4,5.

 

 

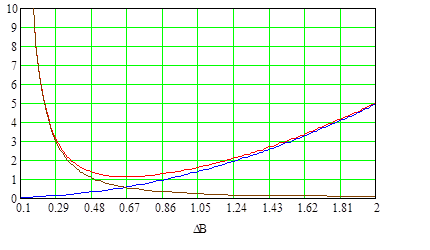
Рис. 2.25

Таблица 2.21. Значения I_μm и P_{вых.макс} при заданных DB_опт и данном λ_о

Размер сердечника	λо	DBопт, Тл	Iμm	Pвых.макс., Вт
2К10х6х3	0,1	0,081	0,2	5,2
	0,3	0,064	0,2	14,1
	0,5	0,052	0,2	21,8
	0,7	0,013	0,2	30,6
2К12х8х3	0,1	0,011	0,2	5,3,
	0,3	0,025	0,2	12,7
	0,5	0,03	0,2	25,5
	0,7	0,55	0,2	57,3
К12х5х5,5	0,1	0,52	0,2	30,1
	0,3	0,6	0,2	42,5
	0,5	0,72	0,2	54,9
	0,7	0,75	0,2	59,1

 

Из таблицы видно, что максимальная выходная мощность сердечников 2К10х6х3, 2К12х8х3, К12х5х5,5 при всех λ_о меньше заданной, значит они не подходят для нашего трансформатора, и дальнейший расчёт для них не ведём.

Рассчитали величины P_т.опт, P_c, P_т по формулам (2.8), (2.14). Полученные данные свели в таблицу.

 

Таблица 2.22. Рассчитанные параметры сердечников

Типоразмер Сердечника	lо	Значения величин
		DBопт, Тл	d	Рс, Вт	Pт.опт, Вт	Pт, Вт	Мт, гр	Vт, см³
K16x10x4,5	0.1	0,98	1,483∙10-3	0,738	1,398	1,218	3,65	1,05
	0.3	0,77	1,476∙10-3	0,86	0,941	0,76	4,93	1,38
	0.5	0,7	1,474∙10-3	1,019	0,813	0,64	6,49	1,78
	0.7	0,67	1,473∙10-3	1,183	0,761	0,58	8,37	2,31

 

По данным таблицы построили зависимости P_т.опт(lо), Р_т(lо), Р_т.макс(lо) на рис. 2.26 и М_т(lо), V_т(lо) на рис. 2.27.

 

График зависимости P_т.опт(lо), Р_т(lо).

 

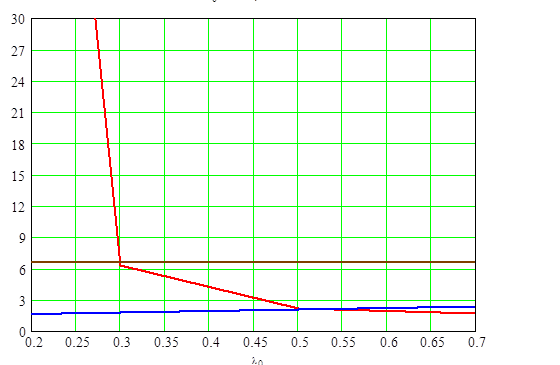
Рис. 2.26

 

График зависимости М_т(lо), V_т(lо).

 

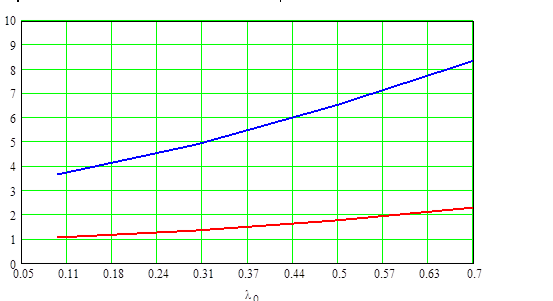
Рис. 2.27

Нашли по точке пересечения графика зависимости Р_с(l_о) и P_т.опт.(l_о) величину l_о: l_о=0,54≈0,5.

При этом l_о сняли с графиков M_т(l_о) и V_т(l_о) массу M_т и объём трансформатора V_т: M_т=6,8 гр; V_т=1,9 см³.

Нашли значения плотностей тока для первичной j₁, вторичной j₂ обмоток[8]:

 

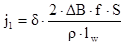,                (2.16)

 

j1 = 1.474·(/2.07·30000·1.35·10^-5/2.38·10^-8·0.02) = 2.952·10⁶ А/м²,

где =  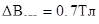– величина магнитной индукции, соответствующей l_о=0,54;

S=0,5·h_c·(D_c-d_c) – площадь сечения сердечника магнитопровода, м²;

S=0,5·4,5·(16–10)=13,5 мм²;

r=[1,75·10^-8(1+0,004·(130–20))]=2,38·10^-8 Ом·мм – удельное электрическое сопротивление материала провода – меди с учетом повышения температуры за счет потерь;

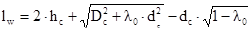 – средняя длина витка обмотки, мм.

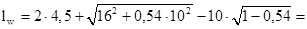20 мм.

 

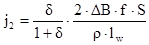, (2.17)

 

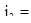2,948·10⁶ А/м².

Определили коэффициент полезного действия η_т нашего трансформатора на выбранном сердечнике К16х10х4,5:

 

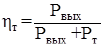 (2.18)

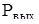=60 – мощность, даваемая трансформатором во вторичную обмотку, Вт;

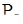=0,813 – мощность потерь в сердечнике при λ_о=0,54 (по формуле 2.14), Вт.

 

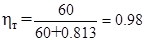
Определили конструктивные данные первичной обмотки.

Число витков первичной обмотки [8]:

 

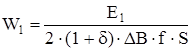.   (2.19)

 

W₁= 600/(2 (1+1.474·10^-3)·30000·0.7·1.35·10^-6) »1050.

Cечение провода в первом приближении:

 

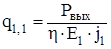                    (2.20)

 

q_1,1 = 60/(0.98·600·2.952·10^-6) = 5.4·10^-8 м².

По найденному сечению провода q_1,1 определили диаметры активного сечения провода без изоляции d_пр и с изоляцией d_из:

d_пр =0,83 мм,

d_из =0,89 мм.

Затем определили коэффициент заполнения сечения обмотки проводом в первом приближении l_п1,1:

 

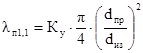                       (2.21)

где К_у – коэффициент укладки. Так как диаметр провода d_пр> 0,3 мм, то К_у=0,9. Подставив значения получили:

l_п1,1 = 0,9·(3,14/4)·(0,83·10^-3/0,89·10^-3)² = 0,644

По известным значениям W₁, q_1,1, l_п1,1 нашли площадь окна сердечника, занятую первичной обмоткой в первом приближении S_1,1:

 

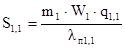.       (2.22)

 

S_1,1 = 23.4∙10^-5 м².

Определили размеры сердечника после изоляции. Количество слоёв изоляции выбрали n=1, толщину изоляции D=0,15 мм. Тогда получим:

 

D_си=D_c+2·D·n=0.017 м,              (2.23)

 

d_си=d_c+2·D·n=0.011 м, (2.24)

 

h_си=h_c+2·D·n=0.005 м. (2.25)

 

Определили коэффициент заполнения окна сердечника обмоткой в первом приближении:

 

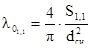.                                (2.26)

 

l_01,1 = 0,975

Нашли среднюю длину витка первичной обмотки в первом приближении:

 

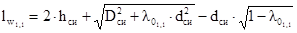=0.028 м  (2.27)

 

Определили во втором приближении сечение провода первичной обмотки:

 

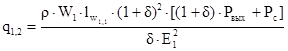=1.329∙10^-7 м². (2.28)

 

Провели цикл вычислений, получили следующие неравенство:

 

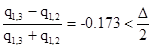, (2.29)

 

расчёт остановили при Δ=0,05.

Определили размеры эквивалентного тороидального сердечника после намотки на него первичной обмотки:

Определили внешний диаметр эквивалентного тороидального сердечника:

 

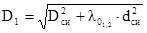,     (2.30)

 

D₁=0,02 м

Нашли внутренний диаметр эквивалентного тороидального сердечника:

 

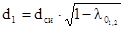,                          (2.31)

 

d₁= 0,004 м,

Определили высоту эквивалентного тороидального сердечника:

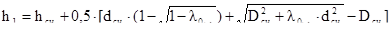. (2.32)

 

h₁=0,011 м.

Определили конструктивные данные вторичной обмотки.

Определили число витков вторичной обмотки:

 

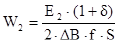.                                    (2.33)

 

W₂₁=530; W₂₂=210; W₂₃=90

Сечение провода в первом приближении:

 

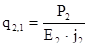.                                         (2.34)

 

q_2,1=0,678∙10^-6 м²;             q_2,2 = 4∙10^-6 м²;         q_2,3 =1,696∙10^-6 м²;

По найденным сечениям проводов определили диаметры активного сечения провода без изоляции d_пр и с изоляцией d_из:

d_пр2,1 = 0,93 мм, d_пр2,2 = 2,26 мм, d_пр2,3 = 1,5 мм,

d_из2,1 = 0,99 мм, d_из2,2 = 2,36 мм, d_из2,3 = 1,58 мм.

Коэффициент заполнения сечения обмотки проводом l_п2,1:

l_п2.1 = 0,62    l_п2.2 = 0,64      l_п2.3 = 0,63.

По известным значениям W₂, q_2,1, l_п2,1 нашли площадь окна сердечника, занятую вторичной обмоткой S_2,1:

 

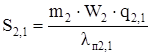.                              (2.35)

 

S_2,1= 1,74∙10^-5 м² S_2,1= 3,93∙10^-5 м² S_2,1= 0,74∙10^-5 м²

Коэффициент заполнения окна сердечника обмоткой нашли по формуле:

 

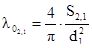.                               (2.36)

 

l_02.1=0,22 l_02.2=0,39 l_02.3=0,15

Нашли среднюю длину витка первичной обмотки:

 

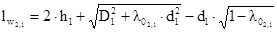.                       (2.37)

 

i_w2,1=24 мм.              i_w2,2=24 мм.    i_w2,3=24 мм.

Нашли во втором приближении сечение провода вторичной обмотки:

 

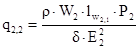                                 (2.38)

 

q_2,21=4,5∙10^-6 м²; q_2,22=1,1∙10^-6 м²; q_2,23=0,6∙10^-6 м².

Провели циклы вычислений, пока не выполнилось неравенство:

 

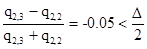,            (2.39)

 

расчёт остановили при Δ=0,05.

Определили размеры эквивалентного тороидального сердечника после намотки на него первичной и вторичной обмоток:

Определили внешний диаметр:

 

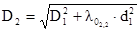,             (2.40)

D₂=20 мм,

Определили внутренний диаметр:

 

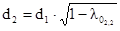,                 (2.41)

 

d₂=3 мм,

Определили высоту:

 

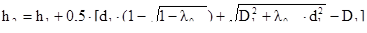 (2.42)

 

h₂=7,4 мм.

В ходе расчета были получены данные трансформатора, соответствующие требуемому. Трансформатор имеет:

P2=60 Вт;

Е1=600 В;

U₂₁=±15 В; U₂₂=5; U₂₃= 12 В;

f =30 кГц;

Т_тмах =130 ⁰С;

m₁=2, m₂=3;

α=0,0014 Вт/см∙ ⁰С;

η_т=98,6%;

I_мmax< 0,2; T_o=40 C.

Сердечник К16´10´4,5, покрытый лаком КФ‑965, и изолированный с торцевой стороны кольцами из картона с обортовкой, и одним слоем из стеклоленты с половинным перекрытием толщиной 0,15 мм.