КАФЕДРА ОБЩЕЙ ФИЗИКИ
Тема: «Моделирование в физике элементарных частиц»
Семипалатинск 2004
Содержание
| Введение | 3 |
| 1. Математическое моделирование в физике | 5 |
| 2. Историческое развитие теории моделирования элементарных частиц | 11 |
| 2.1 Три этапа в развитии физики элементарных частиц | - |
| 2.2 Первые модели элементарных частиц | 13 |
| 2.3 Элементарные частицы и фундаментальные взаимодействия. | 20 |
| 2.4 Современная модель нейтрона | 23 |
| 2.5 Электрический дипольный момент элементарных частиц | 31 |
| 3. Кварковая модель элементарных частиц | 36 |
| 3.1 Существование кварков | - |
| 3.2 Кварковая модель адронов | 40 |
| 4. Практическая часть | 47 |
| 4.1 Методика изучения темы «Элементарные частицы» | 48 |
| 50 | |
| 52 | |
| 57 | |
| 58 | |
| Заключение | 60 |
| Список используемой литературы | 63 |
| Приложения | 64 |
Введение
Информация об элементарных частицах растет день ото дня: сегодня об них известно чрезвычайно много. Однако до сих пор усилия по созданию единой модели этих частиц, позволяющей объяснить все явления, остаются тщетными. Все огромные усилия в этом направлении приводили только к созданию различных моделей, более или менее успешно объясняющих лишь ту или иную группу явлений. И это не должно нас удивлять. Мы знаем, что любая модель в состоянии охватить лишь часть действительности. Мы уже давно убедились в том, что к объектам, размеры которых равны либо меньше длины волны света, давно привычные понятия не применимы. Мир элементарных частиц окружен еще более высоким барьером, чем тот, что стоял перед нами при проникновении в электронную оболочку атома. В этом новом мире все попытки описать явления с помощью наивных наглядных представлений тщетны. «Немыслимым становится реальным событием» - это напоминание призывает нас к особой осторожности.
Современная физика элементарных частиц – это грандиозная наука, где триумфы следуют друг за другом, часто неся взрывной характер, и представляют собой необходимые закономерные фазы беспредельного во времени и пространстве процесса эволюции материи. Всё это необходимо знать современному человеку и понимать, что новые воззрения на строение атома и элементарные частицы явились, прежде всего, результатом блестящего каскада «диковинных» открытий, а сами открытия стали возможны благодаря научно-техническому прогрессу, благодаря оснащению новыми приборами и новыми методами исследования.
В данной работе я попытаюсь ответить на вопрос: Как устроены элементарные частицы? Какие модели элементарных частиц предлагали и выдвигают ученные сегодня?
Совсем недавно в школьных учебниках на уровне молекул и атомов появилось понятие "валентность"; на уровне ядер - понятие дефекта массы, которое позволило рассматривать легкие (даже без массы) объекты построенными из более тяжелых частиц. Дефект масс для ядер сказывается в том, что масса ядер меньше массы нуклонов (нейтронов и протонов) в ядрах, что обусловливает их связь.
В науке на уровне элементарных частиц утвердилось понятие виртуальной частицы, то есть частицы, существующей очень короткое время ~h/m и отлетающей от испускающей ее частицы на расстояние h/p, где m и p - масса и импульс виртуальных частиц. Понятие виртуальной частицы нетривиально. Есть вопрос о правомерности применения к ней слова "существующей". Может быть, это лишь след математического описания? Представление о виртуальной частице как реальности противоречит законам сохранения энергии и импульса. К примеру, когда говорят, что нуклон окружен "шубой" пионов или нуклоны взаимодействуют, обмениваясь пионами, говорят о виртуальных пионах. Существуют ли они? Сегодня можно смело ответить: да. Но на малые промежутки времени и на малых расстояниях. Виртуальные частицы могут - реализоваться, если передать им энергию так, чтобы их образование не противоречило закону сохранения импульса и энергии. Осознание этой возможности приводит к ярким картинам, например движущееся тело с энергией, соответствующей нескольким ГэВ/нуклон, "выворачивает" из вакуума вдоль своей траектории куски вещества и антивещества.
Уже сегодня быстрые протоны образуют пары дейтрон-антидейтрон, гелий-антигелий. Сам вакуум непрерывно кипит, порождая самые разнообразные виртуальные частицы.
На уровне кварков мы встретились с новым, неожиданным и пока до конца непонятым явлением - конфайментом, невылетанием кварков. Кварки, как мы увидим, частицы с дробным электрическим и барионным зарядами и новым квантовым числом - цветом, не могут быть в свободном состоянии, они замкнуты в области порядка размера элементарных частиц. В ряде моделей считается, что кварки "живут" в пузырьках в вакууме и удерживаются поверхностным давлением этих пузырьков.
Уже создана теория, так называемая квантовая хромодинамика, которая описывает поведение кварковых систем в вакууме.
Квантовохромодинамические расчеты на качественном уровне, а для некоторых случаев (например, водородоподобных систем из двух тяжелых кварков) на точном количественном уровне описывают экспериментальные данные.
Понятия о кварках и их свойствах, конечно, непросты и непривычны. Это мировоззренческое достижение современной физики, и потому оно с неизбежностью должно войти в школьные учебники.
1. Математическое моделирование в физике
Понятие модели
Нас окружают сложные технические системы. В процессе проектирования новой или модернизации существующей технической системы решаются задачи расчета параметров и исследования процессов в этой системе. При проведении многовариантных расчетов реальную систему заменяют моделью.
Модель – это материальный или мысленно представленный объект, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.
В широком смысле модель определяют как отражение наиболее существенных свойств объекта.
Математическая модель технического объекта - совокупность математических объектов и отношений между ними, которая адекватно отражает свойства исследуемого объекта, интересующие исследователя.
Хорошо построенная модель доступнее для исследования – нежели реальный объект. Например, недопустимы эксперименты с элементарными частицами для школьников страны в познавательных целях, здесь без модели не обойтись.
Модель может быть представлена различными способами.
инвариантная - запись соотношений модели с помощью традиционного математического языка безотносительно к методу решения уравнений модели;
аналитическая - запись модели в виде результата аналитического решения исходных уравнений модели;
алгоритмическая - запись соотношений модели и выбранного численного метода решения в форме алгоритма.
схемная (графическая) - представление модели на некотором графическом языке (например, язык графов, эквивалентные схемы, диаграммы и т.п.);
физическая
аналоговая
Наиболее универсальным является математическое описание процессов - математическое моделирование.
В понятие математического моделирования включают и процесс решения задачи на ЭВМ.
Методы получения моделей
Получение моделей в общем случае - процедура неформализованная. Основные решения, касающиеся выбора вида математических соотношений, характера используемых переменных и параметров, принимает проектировщик. В тоже время такие операции, как расчет численных значений параметров модели, определение областей адекватности и другие, алгоритмизированы и решаются на ЭВМ. Поэтому моделирование элементов проектируемой системы обычно выполняется специалистами конкретных технических областей с помощью традиционных экспериментальных исследований. Методы получения функциональных моделей элементов делят на теоретические и экспериментальные. Теоретические методы основаны на изучении физических закономерностей протекающих в объекте процессов, определении соответствующего этим закономерностям математического описания, обосновании и принятии упрощающих предположений, выполнении необходимых выкладок и приведении результата к принятой форме представления модели. Экспериментальные методы основаны на использовании внешних проявлений свойств объекта, фиксируемых во время эксплуатации однотипных объектов или при проведении целенаправленных экспериментов. Каким образом происходит построение математической модели?
Во–первых, формулируется цель и предмет исследования.
Во–вторых, выделяются наиболее важные характеристики, соответствующие данной цели.
В–третьих, словесно описываются взаимосвязи между элементами модели.
Далее взаимосвязь формализуется.
И производится расчет по математической модели и анализ полученного решения.
Используя данный алгоритм можно решить любую оптимизационную задачу, в том числе и многокритериальную, т.е. ту в которой преследуется не одна, а несколько целей, в том числе противоречивых. Оптимизационные модели, в том числе многокритериальные, имеют общее свойство– известна цель(или несколько целей) для достижения которой часто приходится иметь дело со сложными системами, где речь идет не столько о решении оптимизационных задач, сколько об исследовании и прогнозировании состояний в зависимости от избираемых стратегий управления. И здесь мы сталкиваемся с трудностями реализации прежнего плана. Они состоят в следующем:
сложная система содержит много связей между элементами
реальная система подвергается влиянию случайных факторов, учет их аналитическим путем невозможен
возможность сопоставления оригинала с моделью существует лишь в начале и после применения математического аппарата, т.к. промежуточные результаты могут не иметь аналогов в реальной системе.
В связи с перечисленными трудностями, возникающими при изучении сложных систем, практика потребовала более гибкий метод, и он появился – имитационное моделирование "Simujation modeling". Обычно под имитационной моделью понимается комплекс программ для ЭВМ, описывающий функционирование отдельных блоков систем и правил взаимодействия между ними. Использование случайных величин делает необходимым многократное проведение экспериментов с имитационной системой (на ЭВМ) и последующий статистический анализ полученных результатов. Таким образом, работа с имитационной системой представляет собой эксперимент, осуществляемый на ЭВМ. В чем же заключаются преимущества?
–Большая близость к реальной системе, чем у математических моделей;
–Блочный принцип дает возможность верифицировать каждый блок до его включения в общую систему;
–Использование зависимостей более сложного характера, не описываемых простыми математическими соотношениями.
Перечисленные достоинства определяют недостатки
–построить имитационную модель дольше, труднее и дороже;
–для работы с имитационной системой необходимо наличие подходящей по классу ЭВМ;
–взаимодействие пользователя и имитационной модели (интерфейс) должно быть не слишком сложным, удобным и хорошо известным;
–построение имитационной модели требует более глубокого изучения реального процесса, нежели математическое моделирование.
Встает вопрос: может ли имитационное моделирование заменить методы оптимизации? Нет, но удобно дополняет их. Имитационная модель – это программа, реализующая некоторый алгоритм, для оптимизации управления которым прежде решается оптимизационная задача.
Итак, ни ЭВМ, ни математическая модель, ни алгоритм для ее исследования порознь не могут решить достаточно сложную задачу. Но вместе они представляют ту силу, которая позволяет познавать окружающий мир, управлять им в интересах человека.
Вычислительная мощность современных компьютеров в сочетании с предоставлением пользователю всех ресурсов системы, возможностью диалогового режима при решении задачи и анализе результатов позволяют свести к минимуму время решения задачи.
При составлении математической модели от исследователя требуется:
изучить свойства исследуемого объекта;
умение отделить главные свойства объекта от второстепенных;
оценить принятые допущения.
Что положительного в любой модели? Она позволяет получить новые знания об объекте, но, к сожалению, в той или иной степени не полна.
Модель описывает зависимость между исходными данными и искомыми величинами. Последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к искомым величинам, называют алгоритмом.
Современная модель нейтрона
Все элементарные частицы, как мы это узнали в предыдущем разделе, в результате строгих испытаний, получают своеобразный аттестат основных свойств. Это величина и знак заряда, масса, время жизни или период полураспада, спин, или момент количества движения и магнитный момент, а также особенности взаимодействия с ядрами.
Нейтрон сверхплотная частица. Его масса, которая в 1839 раз больше массы электрона, превосходит массу протона на 2,5 электронных массы и равна 1,00876 единиц массы, сосредоточена в очень маленьком объеме сферы с радиусом 1,23×10-15м. У него огромная плотность: 200млн. тонн в кубическом сантиметре! Чтобы вообразить такую чудовищную плотность, надо представить себе картину: гора Казбек, спрессованная в чайной ложке. Нейтрон во столько же раз меньше виноградинки, диаметр которой равен 1см, во сколько раз пылинка меньше земного шара.
Заряжен ли нейтрон? Нейтроны, пролетая сквозь вещество, почти не вызывают его ионизации. Они не отталкиваются электрическим полем. Поэтому считают, что заряд нейтрона равен нулю. Но тем не менее, нейтрон окружен магнитным полем, и при встрече с намагниченными телами он отклоняется от своего пути. Поток нейтронов легче проникает через ненамагниченные листы железа. Вероятно, нейтрон должен обладать сложной структурой, раз он обладает магнитным моментом. Нейтрон может испускать p-мезон, что означает, что либо нейтрон в результате какого-то процесса превращается в p-мезон и протон, либо нейтрон представляют собой сложную конструкцию, в состав которой входят p-мезоны и, может быть, другие частицы. Эти явления существенно меняют наши преставления об элементарных частицах, как о каких-то однородных кирпичиках, из которых построены вещества, но и нейтрон, и протон действительно являются элементарными частицами в том смысле, что именно из этих частиц построены ядра всех элементов во вселенной.
Но если под словом «элементарный» понимать простой, далее неразделимый,
то в этом смысле ни нейтрон, ни протон элементарными частицами не являются.
Протон – стабильная частица и может существовать вне ядра. Нейтрон в свободном состоянии существует недолго, распадаясь на протон, электрон и частицу, получившую название антинейтрино.
Распад нейтрона был обнаружен в 1950г в опытах физиков А. Снела (США) и Дж. Робсона (Англия). Еще ранее это явление b-распада наблюдалось у ядер радиоактивных изотопов, но что при этом происходит, оставалось загадкой. Энергия электронов, вылетающих при b-распаде, оказывалась неодинаковой, но всегда меньшей, чем рассчитанная теоретически из уравнения энергобаланса. Кроме того, с вылетом электрона, обладающего определенным механическим моментом, момент образовавшегося ядра должен был, казалось бы, уменьшиться как раз на эту величину. Но и здесь эксперимент расходился с теорией. Чтобы устранить это противоречие, швейцарский физик В. Паули в 1931г высказал гипотезу, что при b-распаде ядра, кроме электрона (позитрона[3]), рождается нейтральная частица (частица «невидимка») с массой покоя, равной или близкой к нулю, уносящая часть энергии и обладающая некоторым моментом количества движения. Ферми ее назвал нейтрино. На основе этой гипотезы он построил теорию, по которой b-распад можно рассматривать как превращение одного из нейтронов ядра в протон, электрон и антинейтрино. Позитронный же b-распад – как превращение протона ядра в нейтрон, позитрон и нейтрино.
Нейтрино оказалось всепроникающей частицей, она не регистрируется приборами, потому что она не несет электрического заряда. Значит, она не способна производить ионизацию атомов, расщепить ядра, то есть не может вызвать эффекты, по которым можно судить о появлении частицы. Нелепо утверждать, будто частица, какой бы необычной она ни была, вообще ни с чем не взаимодействует. Иначе введение такой частицы в физику означало бы замаскированный отказ от закона сохранения энергии. Выходило бы, что энергия теряется вместе с частицей безвозвратно и навсегда. Поэтому Паули предположил, что эта частица просто очень слабо взаимодействует с веществом и поэтому может пройти сквозь большую толщу вещества, не обнаружив себя. Счетчики не могли уловить его, так как из миллиона миллиардов нейтрино, проникающих через километровой толщи броню, лишь одно может прореагировать с ядром брони. Нейтрино было обнаружено только через 26 лет после предсказания его существования. Американские физики Райнс и Коуэн установили счетчик с около реактора, в котором распадающиеся нейтроны ежесекундно рождали больше 5×1019 нейтрино, и зарегистрировали акты взаимодействия их с протонами.
Период полураспада нейтрона, по результатам разных исследований, определяли от 18,8 до 20 минут, но самые точные измерения были проведены советскими ученными П. Е. Спиваком, А. Н. Сосновским и Ю. А. Прокофьевым, которые показали, что время жизни нейтрона в вакууме 11,7 минут или 702 секунды. В этом опыте нейтроны из реактора выпускали в специальную вакуумную трубу. На электрод, расположенный сбоку перпендикулярно оси потока, подавали высокий положительный потенциал. Протоны, возникающие в результате распада нейтронов, отклонялись электрическим полем. Эти протоны, повернув под прямым углом к направлению потока нейтронов, попадали на счетчик, установленный против электрода, и вызывали А отсчётов в минуту. Зная интенсивность потока и определив количество нейтронов, проходящих за минуту мимо электрода N, можно найти постоянную распада нейтрона:
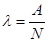
Роль нейтрино не сводится только к объяснению b-распада ядер. Очень многие элементарные частицы в свободном состоянии самопроизвольно распадаются с испусканием нейтрино. Прежде всего, так ведет себя нейтрон. Только в ядрах нейтрон за счет взаимодействия с другими нуклонами приобретает стабильность. Свободный же нейтрон живет в среднем 15 минут. Это было экспериментально доказано лишь после того, как были построены ядерные реакторы, дающие мощные пучки нейтронов.
Как и другие частицы, нейтрино имеет античастицу, называемую антинейтрино. При распаде нейтрона на протон и электрон излучается именно антинейтрино:
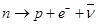
Энергия нейтрона больше суммы энергий протона и электрона. Избыточная энергия уносится с антинейтрино.
Распад нейтрона и других частиц представляет собой превращение в мире элементарных частиц, а не разъединение сложной системы на составные части. Отношение частиц-потомков к частице-предку совсем не напоминает отношение разбитого горшка к целому сосуду. В случае распада нейтрона, например, это очевидно: так как антинейтрино существует лишь в движении по прямой со скоростью света, то оно содержаться внутри нейтрона не может. Возникающие же при распаде нейтрона протон и электрон могут образовывать устойчивую систему. Однако это будет хорошо известный и превосходно изученный атом водорода, а не нейтрон.
Так же обстоит дело и с другими частицами, живущими лишь определенный интервал времени. Распад частицы совсем не является признаком того, что она не элементарна. Нейтрон, несмотря на свою нестабильность, считается элементарной частицей, а ядро атома тяжелого водорода – дейтрон, вне всяких сомнений, состоит из нейтрона и протона, хотя и стабилен.
По современным представлениям, нейтрон – это сложное трехслойное образование с ядром-керном и двойной оболочкой в виде p-мезонных облачков, плотность которых убывает к их периферии до нуля.
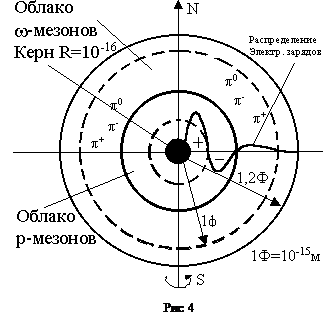 Нейтроны закутаны в облачные «шубы», состоящие из пионов, которыми они постоянно перебрасываются с соседними протонами. Предполагают, что все три слоя нуклона электрически заряжены. Заряды их неодинаковы. В направлении к периферии у нейтрона существуют электроположительный и электроотрицательный слои и они распределяются следующим образом: от центра до половины потенциалы увеличиваются, затем во второй половине слоя уменьшаются и сходят на нет. Радиус керна порядка 0,1 ферми. Во внутреннем облачке нейтрона с радиусом порядка 0,5 ферми рассеяны пионы двойной массы, так называемые би-пионы. Они представляют собой прочно связанные положительные и отрицательные пионы. Необходимость их существования была предсказана математически, и они были названы ро-мезонами (r-мезоны). Также была обоснована вероятность существования другой частицы, состоящей из трех пионов – положительного, отрицательного и нейтрального, названная омега-мезонами (w-мезон). Эти частицы очень недолговечны, они существуют около 10-23 секунд, поэтому их называют моментными образованиями. Третий слой нейтрона состоит из этих три-пионных образований.
Нейтроны закутаны в облачные «шубы», состоящие из пионов, которыми они постоянно перебрасываются с соседними протонами. Предполагают, что все три слоя нуклона электрически заряжены. Заряды их неодинаковы. В направлении к периферии у нейтрона существуют электроположительный и электроотрицательный слои и они распределяются следующим образом: от центра до половины потенциалы увеличиваются, затем во второй половине слоя уменьшаются и сходят на нет. Радиус керна порядка 0,1 ферми. Во внутреннем облачке нейтрона с радиусом порядка 0,5 ферми рассеяны пионы двойной массы, так называемые би-пионы. Они представляют собой прочно связанные положительные и отрицательные пионы. Необходимость их существования была предсказана математически, и они были названы ро-мезонами (r-мезоны). Также была обоснована вероятность существования другой частицы, состоящей из трех пионов – положительного, отрицательного и нейтрального, названная омега-мезонами (w-мезон). Эти частицы очень недолговечны, они существуют около 10-23 секунд, поэтому их называют моментными образованиями. Третий слой нейтрона состоит из этих три-пионных образований.
Было бы ошибкой считать, что только нейтрон имеет такое сложное строение; строение протона не менее сложно, чем нейтрона. В его состав тоже входит положительного знака тяжелый керн, окруженный мезонной оболочкой.
Для изучения структуры нейтрона американские физики Р. Хофштадтер и В. Пановский «просвечивали» дейтерий пучком быстрых электронов, ускоренных до энергии 0,7Гэв[4] и по характеру рассеяния электронов судили о том, какая часть их рассеялась под влиянием нейтронов, а какая часть под влиянием протонов, входящих в состав дейтерия.
Дейтерий представляет довольно «рыхлую» систему, в которой протон удален от нейтрона на сравнительно большое расстояние. На рис 4 показаны распределения электрического заряда и магнитного момента как функции расстояния от центра нейтрона. В нейтроне при простреливании его электронами обнаруживаются разноименно заряженные слои, которые нейтрализуют друг друга. Эти слои состоят из одних и тех же заряженных p-мезонных облаков, действие которых усиливается в случае протона и ослабляется в случае нейтрона.
Одним из первых, кто вместо α-частиц решил использовать нейтроны для обстрела ядер атомов, был молодой итальянский ученный Энрико Ферми. В скромной лаборатории Римского университета Ферми со студентами собрал первую установку для изучению ядерных реакций, вызываемых нейтронами.
Допустим, что бомбардируют нейтронами изотоп натрия с массовым числом 23, ядро которого содержит 11 протонов и 12 нейтронов. При поглощении нейтрона ядром атома натрия-23 энергия ядра увеличивается, оно находится в возбужденном состоянии. При этом потенциальная энергия ядра увеличивается. Такое возбужденное ядро неустойчиво. Избыток энергии возбужденное ядро может выделить путем испускания какой-либо частицы. Реакция идет следующим образом:
23Na+n→24*Na
Ядро 24*Na, находясь в возбужденном состоянии, существует лишь как мгновенная переходная форма (что и изображено звездочкой справа) и распадается с испусканием какой-либо частицы, уносящей избыток энергии. Реакция может произойти в таких вариантах:
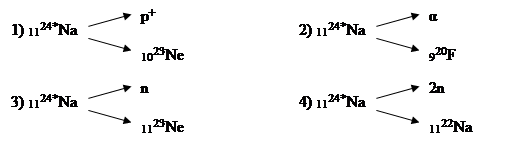 |
Исход реакции зависит от избытка энергии в возбужденном ядре. Так как связь частицы с ядром велика, то может оказаться, что энергии возбуждения ядра недостаточно на испускание частицы. Тогда энергия связи нейтрона выделится в виде γ-кванта:
1124*Na→1124Na+ γ
Характер этого так называемого «захватного» излучения меняется у различных элементов. Поэтому удается определить какой изотоп возникает. Ядро 1124Na «перегружено» нейтронами и не может долго существовать. В нем должны произойти какие-то изменения для того, чтобы оно вновь стало стабильным. Прежде всего, если бы нейтрон вылетел из ядра, то ядро снова стало бы стабильным 1123Na. Но это уже не возможно. Нейтрон не может преодолеть силы сцепления в ядре и вылететь наружу, так как энергия связи уже выделилась в виде γ-излучения. В таблице стабильных изотопов существует элемент, у которого есть стабильный изотоп – 24. Отличается он от радиоактивного тем, что в нем число протонов на 1 больше и число нейтронов на единицу меньше. Масса ядра 1124Na на ничтожную долю больше массы 1224Mg. Это означает, что собственная энергия у 1224Mg меньше чем у 1124Na. То есть при превращении ядра 1124Na в ядро 1224Mg должна выделится энергия. Следовательно, такой процесс может происходить произвольно. Это и есть процесс искусственной радиоактивности, вызванный нейтронами:
1123Na+n*→1124*Na→1224Mg+β-+ν
Причем энергия, уносимая β-частицей а антинейтрино, равна разности энергии ядер: исходного 1124Na и дочернего 1224Mg.
Вначале результаты опытов Ферми были не очень обнадеживающими. При бомбардировке легких элементов новые радиоактивные изотопы получены не были. Были испробованы водород, литий , бериллий, бор, углерод… Никаких результатов. Но когда дело дошло до фтора, то сразу получили очень радиоактивный изотоп. Период полураспада его был около 10 секунд. После этого почти каждый день обнаруживали новый радиоактивный изотоп.
Источник нейтронов приходилось держать достаточно далеко от гейгеровских счетчиков, так как на фоне сильного γ-излучения, свойственного этим источникам нейтронов, нельзя было заметить слабую наведенную радиоактивность. Поэтому счетчики и источник нейтронов были размещены в разных концах длинного коридора. Количества получаемых веществ были столь ничтожны, что ни одним из обычных химических методов анализа нельзя было воспользоваться, поэтому для определения получаемых веществ был разработан новый метод анализа.
Сущность этого метода сводилась к следующему: когда облучали нейтронами, например, железо, предполагали, что возникающая при этом активность обусловлена или радиоактивным изотопом железа, или радиоактивным изотопом какого-либо другого элемента, мало отличающегося от железа по атомному номеру. Добавляя к раствору железа соли элементов, расположенных в таблице Менделеева по соседству с ним, например солей марганца, хрома и кобальта, путем обычных химических методов отделяли от железа эти элементы и определяли, какое из них оказывалось активным. В примере с железом активным оказался раствор с марганцем. Это означает, что при облучении железа нейтронами был получен радиоактивный изотоп марганца.
Но однажды нормальная работа лаборатории была нарушена неожиданностью. В то утро Бруно Понтекорво со своим другом Амальди облучали серебро. Поместив полый серебряный цилиндрик с источником нейтронов в свинцовый ящик, Понтекорво с удивлением обнаружил, что величина полученной активности зависит от того, где находится цилиндрик – в середине ящика или в углу. Попробовали облучать серебро, вне ящика, и тут начались чудеса. Выяснилось, что предметы, находящиеся вблизи от серебра, способны влиять на его активность. При облучении серебряного цилиндра на деревянном столе его активность была больше, чем на мраморном или металлическом. Вся лаборатория вместе с Ферми начала исследовать это загадочное явление. Пробовали различные вещества и смотрели, какие из них способствуют увеличению активности серебра. Взяли большой кусок парафина, внутрь него поместили источник нейтронов. Облучили серебряный цилиндрик. Когда затем этот цилиндрик поднесли к счетчику, то счетчик, к с цепи сорвался, затрещал словно пулемет. Парафин увеличивал искусственную радиоактивность в сотни раз. Ферми предположил, что среда из легких атомов увеличивает активность нейтронов. И действительно, поместив серебряный цилиндрик и источник нейтронов в воду бассейна, обнаружили, что вода тоже во много раз увеличивала искусственную радиоактивность серебра.
Чтобы оценить способность той или иной частицы вызывать ядерную реакцию, необходимо иметь какую-нибудь величину, с помощью которой можно было бы численно выразить эту способность. Такой величиной в физике является эффективное поперечное сечение ядра. Сечение рассматривают как элементарную площадку, которую один нуклон подставляет при встрече другому.
Если бы каждое соударение частицы и ядра приводило бы к ядерной реакции, то вероятность такой реакции была бы равна вероятности столкновений ядра и частицы. Но не каждое столкновение приводит к ядерной реакции, поэтому вероятность ядерной реакции будет еще меньше, чем вероятность столкновения. Условно это можно рассматривать как кажущееся уменьшение сечения ядра, из-за чего столкновения делаются более редкими. В большинстве случаев величина поперечного сечения реакций с быстрыми нейтронами незначительно отличается от геометрического поперечного сечения ядра. Так как диаметр ядра составляет примерно 10-12см, то поперечное его сечение ( 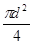 ) удобно измерять в единицах, равных 10-24см2. Это величина носит название барн.
) удобно измерять в единицах, равных 10-24см2. Это величина носит название барн.
Когда мы говорим об эффективном сечении, мы предполагаем, что оно может быть меньше геометрического сечения ядра. Если нейтроны будут находится в тепловом равновесии с замедлителем, то они называются тепловыми нейтронами. Для них оказалось, что эффективное сечение реакции может в тысячи раз превышать геометрическое сечение ядра. Этот факт свидетельствует о том, что в случае медленных нейтронов уже нельзя рассматривать взаимодействие нейтрона с ядром как упругое соударение двух шариков. Ряд понятий «классической механики» пришлось пересматривать, когда исследования коснулись недр атома. Это оказалось связано, прежде всего, с волновыми свойствами частиц. Французский физик Луи де Бройль предположил, что каждой движущейся частице можно сопоставить некую волну, длина которой определяется по формуле:
 ,
,
где h – постоянная Планка, равная 6,62·10-27эрг·с.
Посмотрим какова будет длина волны дробинки массой 1г, летящей со скоростью 600м/с:
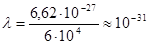 см
см
Столь ничтожна величина длины волны по сравнению с размерами самой дробинки не оказывает никакого влияния, и ее волновые свойства ни в чем не проявляются.
Рассмотрим теперь быстрый нейтрон, имеющий массу m=1,67·10-24кг и энергию 1Мэв. Тогда, определив из формулы 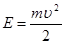 , его импульс
, его импульс 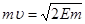 и подставляя его в формулу де Бройля:
и подставляя его в формулу де Бройля:
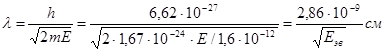
Отсюда мы получаем, что длина волны де Бройля для быстрого нейтрона с энергией 1Мэв будет равна λ=2,86·10-13см.
Как мы видим, длина волны такого быстрого нейтрона не превосходит размеров ядра, и поэтому он ведет себя при столкновениях, как частица.
Определим теперь длину волны теплового нейтрона. Нейтрон, замедлившийся до тепловых скоростей, имеет энергию E=kT, где k – постоянная Больцмана, равная 8,61·10-5эв/градус.
Поэтому нейтрон, замедлившийся до комнатной температуры, имеет энергию Eт=8,6·10-5·290º=0,025эв. Для него длина волны равна:
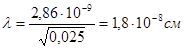
Таким образом, длина волны теплового нейтрона много больше размеров ядра (почти в 60000 раз) и становится сравнимой с размерами атома (d=10-8 см). Даже при энергии 1000эВ длина волны нейтрона, то есть его эффективный диаметр, много больше размеров ядра.
Явления быстрого возрастания эффективного сечения ядра при определенных скоростях нейтронов получило название резонанса. При этом особенно интенсивно происходит передача энергии.
Практическая часть
В настоящее время пока еще мало материала, способствующего усвоению учащимися основных понятий в физике элементарных частиц, поэтому реальный смысл многих из них ускользает от учащихся, что приводит к отсутствию глубоких знаний по предмету. Так довольно трудное понятие свойств элементарных частиц и их строение, оказывается усвоенной ими формально. В данной работе предлагается апробированная методика формирования этих понятий.
Заключение
Физика Элементарных Частиц - или, как ее сейчас чаще называют, Физика Высоких Энергий - одна из областей, составляющих сейчас передний край фундаментальной науки. Исторически Физика Элементарных Частиц образовалась как наука, изучающая и создающая модели вещества на самом глубоком уровне. Однако по мере накопления знаний о структуре материи вопрос "как устроен мир?" сменился вопросом "почему он так устроен?". Такая постановка вопроса - это уже совершенно новый уровень претензии на понимание мира. Возможен ли окончательный и всеохватывающий ответ на этот вопрос? До каких пределов может развиваться наше знание о фундаментальном устройстве мира? Что ждет физику элементарных частиц в будущем?
Двадцатый век стал свидетелем нескольких замечательных моментов синтеза разнородных областей физики. Синтез термодинамики с электродинамикой Максвелла, проведенный М.Планком в 1900 г., положил начало квантовой теории - совершенно новому взгляду на окружающий мир. За ним быстро последовал синтез классической механики и электродинамики (А.Эйнштейн, 1905 г.), приведший к созданию специальной теории относительности. Далее, в 20-х годах из слияния электродинамики с квантовой теорией была создана квантовая электродинамика.
Все это случилось менее чем за 30 лет. Оставшаяся часть 20-го века принадлежала, по существу, эксперименту, который привел к созданию того, что сейчас называется физикой элементарных частиц. В это время было открыто большое количество частиц. Были экспериментально обнаружены сильные и слабые взаимодействия, и лишь позже была понята их роль в микромире. Наконец, к 70-м годам века, картина прояснилась настолько, что стала видна единая природа слабых и электромагнитных взаимодействий. Теория, осуществившая их синтез, - теория электрослабых взаимодействий - явилась фундаментом современной Стандартной Модели Физики Элементарных Частиц. Сильные взаимодействия также поддались описанию с помощью обобщения методов квантовой электродинамики - так родилась квантовая хромодинамика, теория, описывающая "цветовое" взаимодействие кварков и глюонов.
Все эти силы, включая и гравитационные, описываются одним и тем же классом фундаментальных теорий - так называемыми калибровочными теориями. Поведение всех этих сил на малых расстояниях описывается одним и тем же законом: 1/r2. Единственное отличие между разными силами заключается в том, что они "чувствуют" разные характеристики частиц: электрослабые и сильные взаимодействия чувствуют сохраняющиеся "заряды", а гравитационное взаимодействие - также сохраняющуюся энергию. Поэтому в последние годы все усиливается предчувствие, что все четыре взаимодействия имеют единые корни, поэтому в этом направлении возможен новый синтез - Великое Объединение.
Еще один особый вид синтеза, разворачивающийся в настоящее время, - это объединение физики элементарных частиц и космологии. Астрономия и астрофизика 20-го века имеет и свою богатую историю, однако с появлением космологии Большого Взрыва во второй половине века стало ясно, что Физика Элементарных частиц и космология тесно переплетены друг с другом. Их совместное развитие является иллюстрацией того, как тесно связаны физические явления, разворачивающиеся на самых больших расстояниях во Вселенной, с явлениями, происходящими на микроскопически малых расстояниях.
Поэтому, чтобы попытаться увидеть будущее Физики Элементарных частиц, надо понимать, какие достижения можно ожидать во всех трех областях. Можно ли рассчитывать на дальнейший прогресс в физике? Существуют ли его пределы или принципиальные ограничения?
Ключевое слово в Физике Элементарных частиц - это энергия. Типичные экспериментально достижимые энергии сталкивающихся частиц менялись в течение века от нескольких электронвольт (эВ) в первых вакуумных камерах до триллиона эВ (ТэВ) в коллайдере ТэВатрон в лаборатории им. Э.Ферми в Чикаго. Грубо говоря, рост достижимой энергии в 20-м веке был экспоненциальным: энергия удваивалась в среднем каждые 2.5 года.
Сверхвысокие энергии не являются единственным способом узнать новое о природе. Есть особые зоны и при умеренных энергиях, где тщательное и кропотливое изучение тонких эффектов может привести (и приводит!) к открытиям. Такие ускорители называются "фабриками". Они работают на одной энергии и избирательно изучают необычные свойства каких-то конкретных частиц. Так, сейчас имеются " 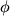 -фабрики", "Z-фабрики" и т.д., работающие на энергиях
-фабрики", "Z-фабрики" и т.д., работающие на энергиях 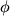 -мезона, Z-бозона и т.д. соответственно. Идея "фабрик" оказалась очень плодотворной, так что в будущем ожидается создание и других фабрик.
-мезона, Z-бозона и т.д. соответственно. Идея "фабрик" оказалась очень плодотворной, так что в будущем ожидается создание и других фабрик.
Принципиально иным направлением экспериментальной Физики Элементарных частиц является неускорительная физика. Идея заключается в том, что в природе и так существуют потоки частиц высокой энергии (иногда даже выше, чем энергии, достижимые на ускорителях), поэтому наша задача - это всего лишь научиться их регистрировать. Два основных класса таких частиц - это заряженные космические лучи внесолнечного происхождения и потоки нейтрино, преимущественно солнечные и атмосферные.
Однако неускорительную физику вряд ли ожидает роль лидера экспериментальной Физики Элементарных частиц - слишком уж неэффективно пассивное экспериментальное наблюдение. Поэтому продолжается поиск принципиально новых возможностей для увеличения энергии линейных коллайдеров. Здесь мы встречаемся с новой принципиальной трудностью. Для того, чтобы разогнать частицу до энергий порядка 1000 ТэВ или выше на типичных дистанциях не более 100 км, требуется создать ускоряющий градиент электрического поля порядка 1 Вольт на ангстрем. Но настолько сильные поля уже будут вырывать электроны из атомов и изменять структуру практически любых материалов. Поэтому при первой же попытке разогнать частицы таким сильным полем сам ускоритель начнет разрушаться!
Есть ли какие-нибудь идеи, как обойти эту трудность? Сейчас мы стоим на пороге новой технологии - нанотехнологии. Не исключено, что будущий прогресс нанотехнологии позволит создать микроскопические ускорительные ячейки с нужным градиентом поля. После разгона частицы и разрушения ячейки смогут регенерироваться за достаточно короткое время, чтобы обеспечить приемлемую интенсивность пучка. Однако это мечты далекого будущего - современная технология на такое не способна.
Обратимся теперь к теоретической физике элементарных частиц. Первый вопрос - объяснение недавно обнаруженных масс и смешивания разных нейтрино. Основной вопрос здесь - почему массы нейтрино столь малы? Как оказалось, что в теории, где характерные массы частиц составляют миллионы и миллиарды эВ, появляются частицы в миллионы раз легче? Предложено несколько моделей объясняющих это явление; среди них выделяется наиболее элегантная, опирающаяся на Великое Объединение. Реализуется ли этот вариант в природе или же это всего лишь красивая теоретическая конструкция? Ближайшее будущее покажет.
Другая важная проблема связана с поиском бозона Хиггса. Теория электрослабого взаимодействия, уже неоднократно подтвержденная экспериментом, неизбежно предсказывает его существование. Однако на опыте хиггсовский бозон пока не открыт. В чем тут дело? Может, он слишком тяжел для современных экспериментов? А может ли теория предсказать его массу? Или же бозона Хиггса вообще нет?
Следующая по очереди проблема - это реализуется или нет в природе Суперсимметрия? Если это так, то мы опять станем свидетелем нового синтеза в Физике Элементарных частиц и пересмотра взглядов на то, как устроен мир.
Наконец, еще одна задача - наиболее сложная из перечисленных - это построение квантовой теории гравитации. На основании тех результатов, которые сейчас появляются в этом направлении, можно судить, что решение этой задачи одновременно даст и ответ на многие фундаментальные вопросы о структуре вещества, пространства, времени: почему в природе существует минимальный электрический заряд? Почему фундаментальные постоянные имеют именно такие, а не иные, значения? Почему наше пространство трехмерно? Почему нам дан именно такой набор элементарных частиц? Физика элементарных частиц еще далека от насыщения. Несмотря на некоторое замедление в ее развитии, в ближайшие 10-15 лет вступит в строй новое поколение ускорителей, что гарантирует нам несколько существенных открытий в Физике элементарных частиц. Это неизбежно приведет к принципиально новому и более глубокому пониманию природы.
Список используемой литературы:
1. Л. Б. Окунь. "Физика элементарных частиц" Москва "Наука" главная редакция физико-математической литературы 1988.
2. Г. Челлен. "Физика элементарных частиц" Издательство "Наука" главная редакция физико-математической литературы 1966.
3. Г. А. Лексин "Соросовский образовательный журнал", N 12, 1996.
4. по докладу Дж.Бьёркена на "Международной Конференции по Фундаментальным наукам: Математическая и Теоретическая Физика", Сингапур, 13-17 Марта 2000.
5. Намбу И. "Почему нет свободных кварков" Успехи физических наук 1978.
6. Зельдович Я.Б. "Классификация элементарных частиц и кварки в изложении для пешеходов" Успехи физ. наук. 1965.
7. "Методика преподавания физики в средней школе" под редакцией С.Е. Каменецкого, Л.А. Ивановой Москва "Просвещение" 1987.
8. С.Ф. Шебалин "Нейтроны" под редакцией доктора физико-математических наук профессора П.А. Ямпольского Просвещение 1969.
9. С.Д. Захаров, И.И, Тугов, Б.Е. Явелов "Физка наших дней" Издательство "Знание" Москва 1977.
10. Г. Линднер «Картины современной физики» Москва «Мир» 1977.
11. Г.Я. Мякишев «Элементарные частицы» Москва «Просвещение» 1973.
12. Дж. Орир «Популярная физика» Москва «Мир» 1969.
[1] Нуклон – общее название для протонов и нейтронов.
[2] 1 ферми – единица ядерной физики, равная 10-15м.
[3] Позитрон – антипод электрона, т.е. электрон, имеющий положительный заряд.
[4] 1 Гэв = 109 эв
КАФЕДРА ОБЩЕЙ ФИЗИКИ
Тема: «Моделирование в физике элементарных частиц»
Семипалатинск 2004
Содержание
| Введение | 3 |
| 1. Математическое моделирование в физике | 5 |
| 2. Историческое развитие теории моделирования элементарных частиц | 11 |
| 2.1 Три этапа в развитии физики элементарных частиц | - |
| 2.2 Первые модели элементарных частиц | 13 |
| 2.3 Элементарные частицы и фундаментальные взаимодействия. | 20 |
| 2.4 Современная модель нейтрона | 23 |
| 2.5 Электрический дипольный момент элементарных частиц | 31 |
| 3. Кварковая модель элементарных частиц | 36 |
| 3.1 Существование кварков | - |
| 3.2 Кварковая модель адронов | 40 |
| 4. Практическая часть | 47 |
| 4.1 Методика изучения темы «Элементарные частицы» | 48 |
| 50 | |
| 52 | |
| 57 | |
| 58 | |
| Заключение | 60 |
| Список используемой литературы | 63 |
| Приложения | 64 |
Введение
Информация об элементарных частицах растет день ото дня: сегодня об них известно чрезвычайно много. Однако до сих пор усилия по созданию единой модели этих частиц, позволяющей объяснить все явления, остаются тщетными. Все огромные усилия в этом направлении приводили только к созданию различных моделей, более или менее успешно объясняющих лишь ту или иную группу явлений. И это не должно нас удивлять. Мы знаем, что любая модель в состоянии охватить лишь часть действительности. Мы уже давно убедились в том, что к объектам, размеры которых равны либо меньше длины волны света, давно привычные понятия не применимы. Мир элементарных частиц окружен еще более высоким барьером, чем тот, что стоял перед нами при проникновении в электронную оболочку атома. В этом новом мире все попытки описать явления с помощью наивных наглядных представлений тщетны. «Немыслимым становится реальным событием» - это напоминание призывает нас к особой осторожности.
Современная физика элементарных частиц – это грандиозная наука, где триумфы следуют друг за другом, часто неся взрывной характер, и представляют собой необходимые закономерные фазы беспредельного во времени и пространстве процесса эволюции материи. Всё это необходимо знать современному человеку и понимать, что новые воззрения на строение атома и элементарные частицы явились, прежде всего, результатом блестящего каскада «диковинных» открытий, а сами открытия стали возможны благодаря научно-техническому прогрессу, благодаря оснащению новыми приборами и новыми методами исследования.
В данной работе я попытаюсь ответить на вопрос: Как устроены элементарные частицы? Какие модели элементарных частиц предлагали и выдвигают ученные сегодня?
Совсем недавно в школьных учебниках на уровне молекул и атомов появилось понятие "валентность"; на уровне ядер - понятие дефекта массы, которое позволило рассматривать легкие (даже без массы) объекты построенными из более тяжелых частиц. Дефект масс для ядер сказывается в том, что масса ядер меньше массы нуклонов (нейтронов и протонов) в ядрах, что обусловливает их связь.
В науке на уровне элементарных частиц утвердилось понятие виртуальной частицы, то есть частицы, существующей очень короткое время ~h/m и отлетающей от испускающей ее частицы на расстояние h/p, где m и p - масса и импульс виртуальных частиц. Понятие виртуальной частицы нетривиально. Есть вопрос о правомерности применения к ней слова "существующей". Может быть, это лишь след математического описания? Представление о виртуальной частице как реальности противоречит законам сохранения энергии и импульса. К примеру, когда говорят, что нуклон окружен "шубой" пионов или нуклоны взаимодействуют, обмениваясь пионами, говорят о виртуальных пионах. Существуют ли они? Сегодня можно смело ответить: да. Но на малые промежутки времени и на малых расстояниях. Виртуальные частицы могут - реализоваться, если передать им энергию так, чтобы их образование не противоречило закону сохранения импульса и энергии. Осознание этой возможности приводит к ярким картинам, например движущееся тело с энергией, соответствующей нескольким ГэВ/нуклон, "выворачивает" из вакуума вдоль своей траектории куски вещества и антивещества.
Уже сегодня быстрые протоны образуют пары дейтрон-антидейтрон, гелий-антигелий. Сам вакуум непрерывно кипит, порождая самые разнообразные виртуальные частицы.
На уровне кварков мы встретились с новым, неожиданным и пока до конца непонятым явлением - конфайментом, невылетанием кварков. Кварки, как мы увидим, частицы с дробным электрическим и барионным зарядами и новым квантовым числом - цветом, не могут быть в свободном состоянии, они замкнуты в области порядка размера элементарных частиц. В ряде моделей считается, что кварки "живут" в пузырьках в вакууме и удерживаются поверхностным давлением этих пузырьков.
Уже создана теория, так называемая квантовая хромодинамика, которая описывает поведение кварковых систем в вакууме.
Квантовохромодинамические расчеты на качественном уровне, а для некоторых случаев (например, водородоподобных систем из двух тяжелых кварков) на точном количественном уровне описывают экспериментальные данные.
Понятия о кварках и их свойствах, конечно, непросты и непривычны. Это мировоззренческое достижение современной физики, и потому оно с неизбежностью должно войти в школьные учебники.
1. Математическое моделирование в физике
Понятие модели
Нас окружают сложные технические системы. В процессе проектирования новой или модернизации существующей технической системы решаются задачи расчета параметров и исследования процессов в этой системе. При проведении многовариантных расчетов реальную систему заменяют моделью.
Модель – это материальный или мысленно представленный объект, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.
В широком смысле модель определяют как отражение наиболее существенных свойств объекта.
Математическая модель технического объекта - совокупность математических объектов и отношений между ними, которая адекватно отражает свойства исследуемого объекта, интересующие исследователя.
Хорошо построенная модель доступнее для исследования – нежели реальный объект. Например, недопустимы эксперименты с элементарными частицами для школьников страны в познавательных целях, здесь без модели не обойтись.
Модель может быть представлена различными способами.
инвариантная - запись соотношений модели с помощью традиционного математического языка безотносительно к методу решения уравнений модели;
аналитическая - запись модели в виде результата аналитического решения исходных уравнений модели;
алгоритмическая - запись соотношений модели и выбранного численного метода решения в форме алгоритма.
схемная (графическая) - представление модели на некотором графическом языке (например, язык графов, эквивалентные схемы, диаграммы и т.п.);
физическая
аналоговая
Наиболее универсальным является математическое описание процессов - математическое моделирование.
В понятие математического моделирования включают и процесс решения задачи на ЭВМ.
Обобщенная математическая модель
Математическая модель описывает зависимость между исходными данными и искомыми величинами. Элементами обобщенной математической модели являются (рис. 1):
множество входных данных (переменные) X,Y;
X - совокупность варьируемых переменных; Y - независимые переменные (константы);
математический оператор L, определяющий операции над этими данными; под которым понимается полная система математических операций, описывающих численные или логические соотношения между множествами входных и выходных данных (переменные);
множество выходных данных (переменных) G(X,Y); представляет собой совокупность критериальных функций, включающую (при необходимости) целевую функцию.

Рис. 1.
Математическая модель является математическим аналогом проектируемого объекта. Степень адекватности ее объекту определяется постановкой и корректностью решений задачи проектирования. Множество варьируемых параметров (переменных) X образует пространство варьируемых параметров Rx (пространство поиска), которое является метрическим с размерностью n, равной числу варьируемых параметров. Множество независимых переменных Y образуют метрическое пространство входных данных Ry. В том случае, когда каждый компонент пространства Ry задается диапазоном возможных значений, множество независимых переменных отображается некоторым ограниченным подпространством пространства Ry. Множество независимых переменных Y определяет среду функционирования объекта, т.е. внешние условия, в которых будет работать проектируемый объект.
Это могут быть:
- технические параметры объекта, не подлежащие изменению в процессе проектирования;
- физические возмущения среды, с которой взаимодействует объект проектирования;
- тактические параметры, которые должен достигать объект проектирования.
Выходные данные рассматриваемой обобщенной модели образуют метрическое пространство критериальных показателей RG.
Схема использования математической модели в системе автоматизированного проектирования показана на рис.2.
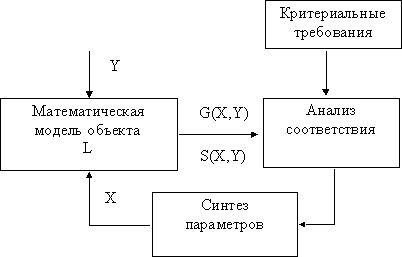
Рис. 2.
Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, универсальности и экономичности.
Адекватность. Модель считается адекватной, если отражает заданные свойства с приемлемой точностью. Точность определяется как степень совпадения значений выходных параметров модели и объекта.
Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. В пространстве внешних параметров выделить область адекватности модели, где погрешность меньше заданной предельно допустимой погрешности. Определение области адекватности моделей - сложная процедура, требующая больших вычислительных затрат, которые быстро растут с увеличением размерности пространства внешних параметров. Эта задача по объему может значительно превосходить задачу параметрической оптимизации самой модели, поэтому для вновь проектируемых объектов может не решаться.
Универсальность - определяется в основном числом и составом учитываемых в модели внешних и выходных параметров.
Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации - затратами машинного времени и памяти.
Противоречивость требований к модели обладать широкой областью адекватности, высокой степени универсальности и высокой экономичности обусловливает использование ряда моделей для объектов одного и того же типа.
Методы получения моделей
Получение моделей в общем случае - процедура неформализованная. Основные решения, касающиеся выбора вида математических соотношений, характера используемых переменных и параметров, принимает проектировщик. В тоже время такие операции, как расчет численных значений параметров модели, определение областей адекватности и другие, алгоритмизированы и решаются на ЭВМ. Поэтому моделирование элементов проектируемой системы обычно выполняется специалистами конкретных технических областей с помощью традиционных экспериментальных исследований. Методы получения функциональных моделей элементов делят на теоретические и экспериментальные. Теоретические методы основаны на изучении физических закономерностей протекающих в объекте процессов, определении соответствующего этим закономерностям математического описания, обосновании и принятии упрощающих предположений, выполнении необходимых выкладок и приведении результата к принятой форме представления модели. Экспериментальные методы основаны на использовании внешних проявлений свойств объекта, фиксируемых во время эксплуатации однотипных объектов или при проведении целенаправленных экспериментов. Каким образом происходит построение математической модели?
Во–первых, формулируется цель и предмет исследования.
Во–вторых, выделяются наиболее важные характеристики, соответствующие данной цели.
В–третьих, словесно описываются взаимосвязи между элементами модели.
Далее взаимосвязь формализуется.
И производится расчет по математической модели и анализ полученного решения.
Используя данный алгоритм можно решить любую оптимизационную задачу, в том числе и многокритериальную, т.е. ту в которой преследуется не одна, а несколько целей, в том числе противоречивых. Оптимизационные модели, в том числе многокритериальные, имеют общее свойство– известна цель(или несколько целей) для достижения которой часто приходится иметь дело со сложными системами, где речь идет не столько о решении оптимизационных задач, сколько об исследовании и прогнозировании состояний в зависимости от избираемых стратегий управления. И здесь мы сталкиваемся с трудностями реализации прежнего плана. Они состоят в следующем:
сложная система содержит много связей между элементами
реальная система подвергается влиянию случайных факторов, учет их аналитическим путем невозможен
возможность сопоставления оригинала с моделью существует лишь в начале и после применения математического аппарата, т.к. промежуточные результаты могут не иметь аналогов в реальной системе.
В связи с перечисленными трудностями, возникающими при изучении сложных систем, практика потребовала более гибкий метод, и он появился – имитационное моделирование "Simujation modeling". Обычно под имитационной моделью понимается комплекс программ для ЭВМ, описывающий функционирование отдельных блоков систем и правил взаимодействия между ними. Использование случайных величин делает необходимым многократное проведение экспериментов с имитационной системой (на ЭВМ) и последующий статистический анализ полученных результатов. Таким образом, работа с имитационной системой представляет собой эксперимент, осуществляемый на ЭВМ. В чем же заключаются преимущества?
–Большая близость к реальной системе, чем у математических моделей;
–Блочный принцип дает возможность верифицировать каждый блок до его включения в общую систему;
–Использование зависимостей более сложного характера, не описываемых простыми математическими соотношениями.
Перечисленные достоинства определяют недостатки
–построить имитационную модель дольше, труднее и дороже;
–для работы с имитационной системой необходимо наличие подходящей по классу ЭВМ;
–взаимодействие пользователя и имитационной модели (интерфейс) должно быть не слишком сложным, удобным и хорошо известным;
–построение имитационной модели требует более глубокого изучения реального процесса, нежели математическое моделирование.
Встает вопрос: может ли имитационное моделирование заменить методы оптимизации? Нет, но удобно дополняет их. Имитационная модель – это программа, реализующая некоторый алгоритм, для оптимизации управления которым прежде решается оптимизационная задача.
Итак, ни ЭВМ, ни математическая модель, ни алгоритм для ее исследования порознь не могут решить достаточно сложную задачу. Но вместе они представляют ту силу, которая позволяет познавать окружающий мир, управлять им в интересах человека.
Вычислительная мощность современных компьютеров в сочетании с предоставлением пользователю всех ресурсов системы, возможностью диалогового режима при решении задачи и анализе результатов позволяют свести к минимуму время решения задачи.
При составлении математической модели от исследователя требуется:
изучить свойства исследуемого объекта;
умение отделить главные свойства объекта от второстепенных;
оценить принятые допущения.
Что положительного в любой модели? Она позволяет получить новые знания об объекте, но, к сожалению, в той или иной степени не полна.
Модель описывает зависимость между исходными данными и искомыми величинами. Последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к искомым величинам, называют алгоритмом.
Дата: 2019-05-28, просмотров: 333.