Теплофізичні властивості полімерів залежать від їх будови і особливостей протікання молекулярно-кінетичних процесів на молекулярному і надмолекулярному рівнях.
При розгляді процесу теплопровідності в полімерах використовують уявлення про теплоперенос в діелектриках. В полімерах розглядають два механізми теплопереносу:
1. Дифузійний перенос, згідно якого отримуються низькі значення l.
2. Зумовлений вібрацією енергетичних структур, при яких термозбудження виникає в у вигляді фононів, що призводить до більш ефективної передачі тепла.
Для чистого ПВХ температурна залежність l добре лписується емпіричним рівнянням:
l=l0=1,36×104Т –0,2×10-6Т2, де
l0 – коефіцієнт теплопровідності ПВХ, рівний 0,148 Вт/м×К при Т = 290К.
Для розрахунку l композицій використовують принцип узагальненої теплопровідності, враховуючи, що характерною особливістю структури таких систем являється неперервність полімерної матриці в довільному напрямку і дискретне розміщення частинок наповнювача, а також існування граничного шару на межі поділу фаз.
Під час визначення ефективного коефіцієнта теплопровідності випливає, що його значення залежить від коефіцієнта теплопровідності граничного шару[1], а саме l для елементарної комірки рівний:
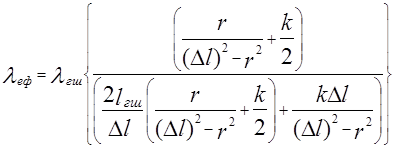(6)
У формулі (6) фігурує ефективна товщина ГШ –, яка являється однією з кількісних мір взаємодії полімера з наповнювачем.
Визначення lгш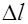 
дозволяє розрахувати об’ємний вміст граничного шару у гетерогенній полімерній системі. Розглянемо метод її визначення запропонований у [1].
В наповнених полімерних системах дисперсна частинка наповнювача оточена ГШ, що являє собою третю компоненту. В області вмісту наповнювача менш критичного (jн<jкр) високодисперсний наповнювач не знаходиться в вузлах регулярної структури, займає випадкові положення в просторі. Хаотичне розміщення частинок наповнювача, в цьому випадку, важко визначити математично, як це можна зробити в кристалічній решітці. Однак, при jн<jкр наповнену систему можна як і раніше моделювати вигляді сукупності частинок наповнювача, розділених полімерним прошарком lп, на яких адсорбований ГШ товщиною lгш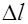
.. Таким чином, L= lп+ 2lгш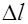
., де L – відстань між двома частинками наповнювача.
В міру зростання вмісту наповнювача в системі все більша кількість полімерної матриці переходить в стан ГШ. Із рівняння адсорбційної ізотерми слідує, що маса ГШ m1 в розрахунку на полімер рівна:
m1= М(1 – е-aN) (7)
де a – коефіцієнт пропорційності, N – число частинок наповнювача, М – маса полімерної матриці.
Розглянувши ГШ, як сферичний прошарок товщини lгш отримаємо, що ефективний об’єм ГШ полімерної системи, що містить N частинок наповнювача, буде рівним:
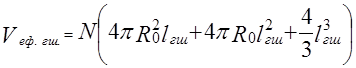, (8)
Із рівняння (7) маємо:
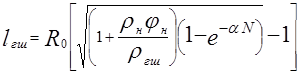(9)
Коефіцієнт a визначимо, як міру активності наповнювача, на основі стрибка теплоємності для наповненого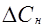 
і ненаповненого 
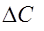полімера:
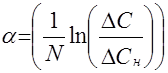(10)
При jкр £ jн трикомпонентна система виродиться в двохкомпонентну типу наповнювач-ГШ. Коли буде виконуватись умова jкр = jн, а це можливо для рівномірно диспергованих частинок в полімері, отримаємо залежність:
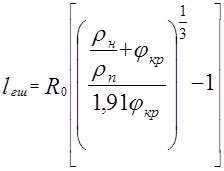(11)
де rп – густина полімерної матриці.
Підсумовуючи необхідно відмітити, що об’ємний вміст граничного шару на межі розподілу фаз полімера і наповнювача впливає на такі теплофізичні характеристики полімерної композиції, як ефективний коефіцієнт теплопровідності та інші.
Аналізуючи результати оцінки (табл. 2.3-1), отримані у [1] під час вимірювання lгш можна зробити наступні висновки.
Табл. 2.3‑1
| Композиція | jоб, % | lгш, Вт/м ×К | Композиція | jоб, % | lгш, Вт/м ×К |
| ПВХ+W | 0,07 | 0,18 | ПВХ+Cu | 0,12 | 0,26 |
| 0,22 | 0,23 | 0,38 | 0,29 | ||
| 0,37 | 0,24 | 0,64 | 0,32 | ||
| 2,90 | 0,34 | 1,40 | 0,37 | ||
| 6,60 | 0,39 | 5,00 | 0,47 | ||
| 9,50 | 0,42 | 11,00 | 0,52 | ||
| 14,10 | 0,45 | 16,60 | 0,57 | ||
| 21,90 | 0,47 | 22,30 | 0,61 | ||
| 38,70 | 0,50 | 33,10 | 0,64 | ||
| 50,10 | 0,55 | 50,30 | 0,70 | ||
| 60,30 | 0,62 | 60,10 | 0,81 |
Отримані результати по визначення ефективного коефіцієнта теплопровідності граничних шарів ПВХ і ПВБ систем представлені в
табл. 2.3-1. Із аналізу якої слідує, що з підвищенням концентрації наповнювача в композиції спостерігається зміна lгш. Так, для систем ПВХ по мірі збільшення вмісту W або Cu в композиції lгш зростає в усьому діапазоні концентрацій наповнювача. При цьому lгш залишається більшим l ПВХ. Крім того, lгш близький до l ПВХ-систем У випадку ІІВБ-композицій при вмісті наповнювача меншому за критичний має місце екстремальне значення lгш . Найбільш суттєві зміни lгш спостерігаються при вмісті W чи Сu до 6 об. %. Саме для цієї області вмісту низькомолекулярних наповнювачів відмічається найбільш інтенсивна зміна ряду інших властивостей композицій. При подальшому збільшенні вмісту W і Сu в системі lгш після досягнення екстремального значення має тенденцію до зменшення до області 15 у 20 об. % наповнювача. Наступне збільшення вмісту високодисперсного W чи Сu знову приводить до росту lгш . Таку залежність можна пояснити "конкуруючими" ефектами, зв'язаними з зміцненням і розрихлюючою дією поверхні наповнювача на полімерну матрицю. Значить, чим більш активний наповнювач у відношенні до ПВХ чи ПВБ, тим більш інтенсивно, в області незначного вмісту (до 6 об. %), проявляється роль ГШ в формуванні теплофізичних властивостей композицій.
ВИСНОВКИ.
Введення наповнювача в полімер призводить до утворення речовин, властивості яких значно відрізняються від ненаповненого полімера. Наповнення полімера високодисперсними матеріалами характеризується виникненням фазового шару.
Граничний шар – це прошарок полімера, властивості якого змінюються під дією поверхні в порівнянні з властивостями полімера або наповнювача в об’ємі. Цей міжфазний шар характеризується деякими досить умовними параметрами: товщина граничного шару, коефіцієнт теплопровідності. Визначити ці параметри безпосередньо дуже складно, тому їх визначають на основі інших характеристик.
Встановлено, що існування межі поділу призводить до суттєвих змін релаксаційної поведінки полімера в міжфазному прошарку, зміні температур склування полімера і також інших властивостей полімерної системи.[3] Все це зв’язано з зміною густини молекулярної упаковки, а також з зменшенням рухливості сегментів полімерних ланцюгів і більших кінетичних елементів внаслідок їх взаємодії з твердою поверхнею.
Властивості гетерогенних полімерних систем визначаються кількістю полімера, який знаходиться в міжфазному прошарку. Кількісний зв’язок між властивостями міжфазного шару, об’ємним вмістом наповнювача і комплексом властивостей полімерних композицій потребує подальшого вивчення.
ВИКОРИСТАНА ЛІТЕРАТУРА.
1.Колупаєв Б.С., Ліпатов Ю.С., Бордюк М.А., Дем’янюк Б.П. Вивчення полімерних матеріалів в загальноосвітній школі: навчальний посібник. – Рівне, 1993 р., 92 с.
2.Колупаев Б.С. Релаксационные и термические свойства наполненных полимерных систем. - Львов: Вища школа, 1980.
3.Липатов Ю.С. Физико-химические основы наполнения полимеров. - М.: Химия, 1991.
4.Дулънев Γ.H„ Новиков В.В. Процессы переноса в неоднородных средах .- Л.: Энергоатомиздат, 1991.
5.Бордюк М.А. Волошин О.М., Колупаев Б.С., Липатов Ю.С.//УФЖ.- 1996- 41, № 4 -c.438-441.
6.Годовский Ю.К. Теплофизика полимеров,- М.: Химия, 1982.
7.Колупаев Б.С. Физико-химия полимеров,- Львов: Вища школа, 1976.
8.Колупаев Б.С; Демьянюк Б.П., Муха Б.И. Бордюк Н.А. //Композиц. полимер. материалы- 1984 - Вып. 23 - с.20-23.
9.Бордюк Н.А., Колупаее Б.С., Волошин О.М. // Физика и техника высоких давлений.-1995-№3-с.49-58.
10. Колупаєв Б.С., Бордюк М.А., Ліпатов Ю.С. //Доп. НАН України - 1995 - № 8 -с. 112-114.
11. Кравченко С. Мониторы завтрашнего дня.//Chip. №11 – 1999 р., ст.24-26.
Дата: 2019-05-28, просмотров: 190.
