1. Занесены исходные данные (таб. 1.5.1)
Таблица 1.5.1 – Исходные данные
| Число жителей в городе | M | 1000000 | |
| Коэффициент ажиотажа | KA | 0,0000001 | |
| Ежедневные расходы (руб.) | R | 300 | |
| Среднее время между покупкой и продажей акции (дни) | T | 50 | |
| Норма прибыли (ежедневный процент от суммы в кассе) | S | 3 | |
| Состояние на первый день: |
|
| |
|
| начальный капитал (руб.) | П1 | 70000 |
|
| число купивших акции в первый день | SNK1 | 7 |
2. Сформирована таблица из граф: День; Курс продаж; Продано в день; Продано всего; Курс покупки; Куплено в день; Куплено всего; Сумма в кассе; Доход в день; Доход всего. Ссылки на исходные данные осуществлены в виде абсолютных ссылок.
3. Заполнены графы
- День с помощью авто заполнения с 1 до 365.
- Курс продажи с 1,05 до 8,33 с шагом 0,02.
- Курс покупки с 1,00 до 8,28 с шагом 0,02.
- Продано в день акций:
-
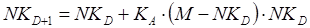 ,
,
где M – число жителей в городе;
NKD – общее число купивших акции на день D;
KA – коэффициент ажиотажа.
Число акций не может быть дробным, поэтому к нему применяется функция ОКРУГЛВВЕРХ() (ОКРУГЛВВЕРХ(C3+$H$3*($H$2-C3)*C3;0)).
- Продано всего просчитана как сумма проданных акций.
- Куплено в день заполнена путем: если D ≤ T (среднее время между покупкой и продажей акций жителями), то NPD+1 = 0, в противном случае смещается на T дней от продажи. (СМЕЩ (NKD; -50,0)).
- Количество купленных акций также считается суммой.
- Сумма в кассе в первый день равна 70000 (П1). Следующие дни просчитаны:
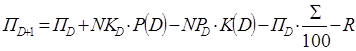 ,
,
где Σ – норма прибыли;
R – ежедневные расходы.
- Доход в день просчитан как
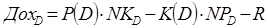
- Доход всего просчитан как сумма дохода предыдущих дней.
- Доход организации равен произведению суммы в кассе на норму прибыли (=H4*'Исхидные данные'!$H$6/100).
4. Построен график изменения количества денег в кассе и доходов организаторов пирамиды за 50 дней и за год (Приложение А, Б).
5. Определен максимальный доход фирмы с помощью функции (3369519,74 руб.)
МАКС (Число1; Число 2; …)
6. Определен день достижения данного дохода с помощью функции (149 день)
ПОИСКПОЗ(Искомое_значение; Просматриваемый_массив;
Тип_ сопоставления),
где Искомое_значение – значение, используемое при поиске нужного значения в массиве;
Просматриваемый_массив – непрерывный диапазон ячеек, просматриваемый в поиске искомого значения.
Тип_сопоставления – число (1,0,-1), определяющее возвращаемое значение.
7. Определена минимальная сумма в кассе.
8. Подобрано такое минимальное значение начального капитала, которое бы позволило не уйти в отрицательную сумму в кассе на начальном этапе развития, с помощью функции Подбор параметра (9866,89 руб.). При этом минимальная сумма в кассе должна стать равной 0,00р.
9. Прослежено изменение дохода организатора пирамиды в определенный день Х, изменяя исходные данные. День X задан самостоятельно (50).
10. Полученные данные занесены в таблицу (таб. 1.5.2).
Таблица 1.5.2 – Результаты исследования
| Изменяемый параметр | Увеличиваемый параметр | Уменьшаемый параметр | ||||
| Значение | День Х | Доходы на день Х | Значение | День Х | Доходы на день Х | |
| Исходное значение |
| 735,83 |
|
| 735,83 | |
| M | 2000000 | 50 | 17961,56 | 600000 | 50 | 377,35 |
| KA | 0,00000017 | 50 | 6446,68 | 0,00000006 | 50 | 377,35 |
| R | 370 | 50 | 681,56 | 250 | 50 | 774,59 |
| T | 55 | 50 | 735,83 | 45 | 50 | 733,93 |
| S | 6% | 50 | 739,86 | 2,5% | 50 | 721,08 |
| П1 | 100000 | 50 | 938,16 | 65000 | 50 | 702,11 |
| SNK1 | 12 | 50 | 989,59 | 5 | 50 | 648,65 |
Процесс описывается дифференциальным уравнением.
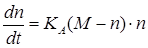
Также найдены максимальный доход и день его достижения, минимальное значение первоначального капитала.
Дата: 2019-05-28, просмотров: 306.