Изображение X(s)
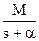
Закон изменения выходного сигнала обычно является функцией, которую необходимо найти, а входной сигнал, как правило, известен. Некоторые типовые входные сигналы были рассмотрены в п. 2.3. Здесь приводятся их изображения:
единичное ступенчатое воздействие имеет изображение X(s) =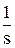 
,
дельта-функция X(s) = 1,
линейное воздействие X(s) =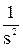 
.
Пример. Решение ДУ с использованием преобразований Лапласа.
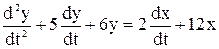
Допустим, входной сигнал имеет форму единичного ступенчатого воздействия, т.е. x(t) = 1. Тогда изображение входного сигнала X(s) =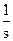 
.
Производим преобразование исходного ДУ по Лапласу и подставляем X(s):
s2Y + 5sY + 6Y = 2sX + 12X,
s2Y + 5sY + 6Y = 2s 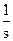+ 12 ,
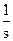Y(s3 + 5s2 + 6s) = 2s + 12.
Определяется выражение для Y:
.
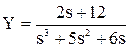Оригинал полученной функции отсутствует в таблице оригиналов и изображений. Для решения задачи его поиска дробь разбивается на сумму простых дробей с учетом того, что знаменатель может быть представлен в виде s(s + 2)(s + 3):
= 
= 
+ 
+ 
=
= 
.
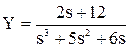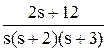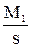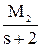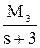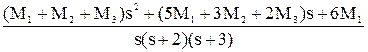Сравнивая получившуюся дробь с исходной, можно составить систему из трех уравнений с тремя неизвестными:
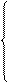
М1 + М2 + М3 = 0 M1 = 2
5.М1 + 3.М2 + 2.М3 = 2 à M2 = -4
6.М1 = 12 M3 = 2
Следовательно, дробь можно представить как сумму трех дробей:
= 
- 
+ 
.
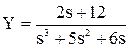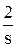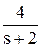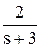Теперь, используя табличные функции, определяется оригинал выходной функции:
y(t) = 2 - 4.e-2t + 2.e-3t. ¨
2.6. Передаточные функции.
2.6.1 Определение передаточной функции.
Преобразование ДУ по Лапласу дает возможность ввести удобное понятие передаточной функции, характеризующей динамические свойства системы.
Например, операторное уравнение
3s2Y(s) + 4sY(s) + Y(s) = 2sX(s) + 4X(s)
можно преобразовать, вынеся X(s) и Y(s) за скобки и поделив друг на друга:
Y(s)*(3s2 + 4s + 1) = X(s)*(2s + 4)
.
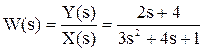Полученное выражение называется передаточной функцией.
Передаточной функцией называется отношение изображения выходного воздействия Y(s) к изображению входного X(s) при нулевых начальных условиях.
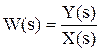(2.4)
Передаточная функция является дробно-рациональной функцией комплексной переменной:
,
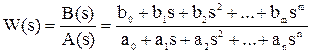где B(s) = b0 + b1s + b2 s2 + … + bm sm - полином числителя,
А(s) = a0 + a1s + a2 s2 + … + an sn - полином знаменателя.
Передаточная функция имеет порядок, который определяется порядком полинома знаменателя (n).
Из (2.4) следует, что изображение выходного сигнала можно найти как
Y(s) = W(s)*X(s).
Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета АСР сводится к определению ее передаточной функции.
2.6.2 Примеры типовых звеньев.
Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.
Простейшие типовые звенья:
· усилительное,
· интегрирующее,
· дифференцирующее,
· апериодическое,
· колебательное,
· запаздывающее.
1) Усилительное звено.
Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.
Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз (см. рис. 1.15).
Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.
2) Интегрирующее.
2.1) Идеальное интегрирующее.
Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины.
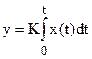; W(s) =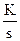 
При подаче на вход звена воздействия выходной сигнал постоянно возрастает (см. рис. 1.16).
Это звено астатическое, т.е. не имеет установившегося режима.
2.2) Реальное интегрирующее.
Передаточная функция этого звена имеет вид:
W(s) =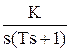 
.
Переходная характеристика в отличие от идеального звена является кривой (см. рис. 1.17).
Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора.
3) Дифференцирующее.
3.1) Идеальное дифференцирующее.
Выходная величина пропорциональна производной по времени от входной:
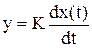; W(s) = K*s
При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию).
3.2) Реальное дифференцирующее.
Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям. Переходная характеристика и передаточная функция этого звена имеют вид:
W(s) =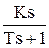 
.
4) Апериодическое (инерционное).
Этому звену соответствуют ДУ и ПФ вида:
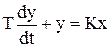; W(s) = 
.
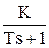Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х0.
Изображение ступенчатого воздействия: X(s) =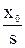 
. Тогда изображение выходной величины:
Y(s) = W(s) X(s) =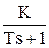 
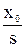= K x0 
.
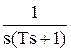Разложим дробь на простые:
= 
+ 
= 
= 
- 
= - 
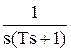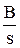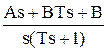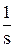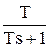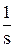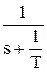
Оригинал первой дроби по таблице: L-1{ 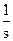} = 1, второй:
L-1{ } =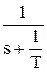 
.
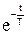Тогда окончательно получаем:
y(t) = K x0 (1 - ).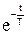
Постоянная Т называется постоянной времени.
Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону (см. рис. 1.19).
5) Колебательное звено имеет ДУ и ПФ вида
,
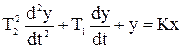W(s) =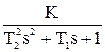 
.
При подаче на вход ступенчатого воздействия амплитудой х0 на переходная кривая будет
иметь один из двух видов: апериодический (при Т1 ³ 2Т2) или колебательный (при Т1 < 2Т2).
6) Запаздывающее.
y(t) = x(t - t), W(s) = e-ts.
Выходная величина у в точности повторяет входную величину х с некоторым запаздыванием t. Примеры: движение груза по конвейеру, движение жидкости по трубопроводу.
2.6.3 Соединения звеньев.
Поскольку исследуемый объект в целях упрощения анализа функционирования разбит нами на звенья, то после определения передаточных функций для каждого звена встает задача объединения их в одну передаточную функцию объекта. Вид передаточной функции объекта зависит от последовательности соединения звеньев:
1) Последовательное соединение.
Wоб = W1.W2.W3…
При последовательном соединении звеньев их передаточные функции перемножаются.
2) Параллельное соединение.
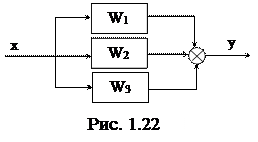Wоб = W1 + W2 + W3 + …
При параллельном соединении звеньев их передаточные функции складываются.
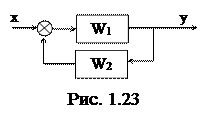3) Обратная связь
Передаточная функция по заданию (х):
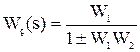
«+» соответствует отрицательной ОС,
«-» - положительной.
Для определения передаточных функций объектов, имеющих более сложные соединения звеньев, используют либо последовательное укрупнение схемы, либо преобразуют по формуле Мезона.
2.6.4 Передаточные функции АСР.
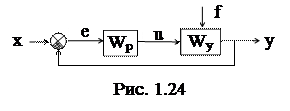Для исследования и расчета структурную схему АСР путем эквивалентных преобразований приводят к простейшему стандартному виду «объект - регулятор».
Это необходимо, во-первых, для того, чтобы определить математические зависимости в системе, и, во-вторых, как правило, все инженерные методы расчета и определения параметров настройки регуляторов применены для такой стандартной структуры.
В общем случае любая одномерная АСР с главной обратной связью путем постепенного укрупнения звеньев может быть приведена к такому виду.
Если выход системы у не подавать на ее вход, то мы получим разомкнутую систему регулирования, передаточная функция которой определяется как произведение:
W¥ = Wp.Wy
(Wp - ПФ регулятора, Wy - ПФ объекта управления).
То есть последовательность звеньев Wp и Wy может быть заменена одним звеном с W¥. Передаточную функцию замкнутой системы принято обозначать как Ф(s). Она может быть выражена через W¥:
Фз(s) =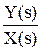 
= 
.
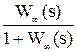(далее будем рассматривать только системы с обратной отрицательной связью, поскольку они используются в подавляющем большинстве АСР).
Данная передаточная функция Фз(s) определяет зависимость у от х и называется передаточной функцией замкнутой системы по каналу задающего воздействия (по заданию).
Для АСР существуют также передаточные функции по другим каналам:
Фe(s) =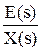 
= 
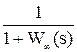- по ошибке,
Фв(s) =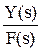 
= 
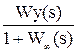- по возмущению.
Поскольку передаточная функция разомкнутой системы является в общем случае дробно-рациональной функцией вида W¥ =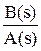 
, то передаточные функции замкнутой системы могут быть преобразованы:
Фз(s) =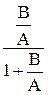 
= 
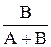, Фe(s) = 
= 
.
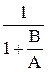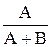Как видно, эти передаточные функции отличаются только выражения ми числителей. Выражение знаменателя называется характеристическим выражением замкнутой системы и обозначается как Dз(s) = A(s) + B(s), в то время как выражение, находящееся в числителе передаточной функции разомкнутой системы W¥, называется характеристическим выражением разомкнутой системы B(s).
2.6.5 Определение параметров передаточной функции объекта по переходной кривой.
Процесс получения передаточной функции объекта, исходя из данных о переходном процессе, называется идентификацией объекта.
Предположим, что при подаче на вход некоторого объекта ступенчатого воздействия была получена переходная характеристика (см. рис. 1.26). Требуется определить вид и параметры передаточной функции.
Предположим, что передаточная функция имеет вид
,
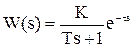(инерционной звено с запаздыванием).
Параметры передаточной функции:
К - коэффициент усиления,
Т - постоянная времени,
t - запаздывание.
Коэффициентом усиления называется величина, показывающая, во сколько раз данное звено усиливает входной сигнал (в установившемся режиме), и равна отношению выходной величины у в установившемся режиме ко входной величине х:
,
Установившееся значение выходной величины ууст - это значение у при t ® ¥.
Запаздыванием t называется промежуток времени от момента изменения входной величины х до начала изменения выходной величины у.
Постоянная времени Т может быть определена несколькими методами в зависимости от вида передаточной функции. Для рассматриваемой передаточной функции 1-го порядка Т определяется наиболее просто: сначала проводится касательная к точке перегиба, затем находятся точки пересечения с осью времени и асимптотой yуст; время Т определяется как интервал времени между этими точками.
В случае, если на графике между точкой перегиба имеется вогнутость, определяется дополнительное запаздывание tдоп, которое прибавляется к основному: t = t + tдоп.
2.7. Частотные характеристики.
2.7.1 Определение частотных характеристик.
Известно, что динамические процессы могут быть представлены частотными характеристиками (ЧХ) путем разложения функции в ряд Фурье.
Предположим, имеется некоторый объект и требуется определить его ЧХ. При экспериментальном снятии ЧХ на вход объекта подается синусоидальный сигнал с амплитудой Авх = 1 и некоторой частотой w, т.е.
x(t) = Авхsin(wt) = sin(wt).
Тогда после прохождения переходных процессов на выходе мы будем также иметь синусоидальный сигналтой же частоты w, но другой амплитуды Авых и фазы j:
у(t) = Авыхsin(wt + j)
При разных значениях w величины Авых и j, как правило, также будут различными. Эта зависимость амплитуды и фазы от частоты называется частотной характеристикой. Виды ЧХ:
· 
АФХ - зависимость амплитуды и фазы от частоты (изображается на комплексной плоскости);
· АЧХ - зависимость амплитуды от частоты;
· ФЧХ - зависимость фазы от частоты;
· ЛАХ, ЛАЧХ - логарифмические АЧХ.
На комплексной плоскости входная величина x = Авх.sin(wt) для каждого момента времени ti определяется вектором х на комплексной плоскости. Этот вектор имеет длину, равную Авх, и отложен под углом wti к действительной оси. (Re - действительная ось, Im - мнимая ось)
Тогда величину х можно записать в комплексной форме
х(t) = Авх(cos(wt) + j.sin(wt)),
где j =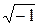 
- мнимая единица.
Или, если использовать формулу Эйлера eja = cosa + j.sina, то можно записать
х(t) = Авх.ejwt.
Выходной сигнал y(t) можно аналогично представить как вектор
y(t) = Авых.ej(wt+j).
Рассмотрим связь передаточной функции и частотной характеристики.
Определим производные по Лапласу:
у ® Y
у’ ® sY
у” ® s2Y и т.д.
Определим производные ЧХ:
у’(t) = jw Авыхеj(wt + j) = jw у,
у”(t) = (jw)2 Авыхеj(wt + j) = (jw)2 у и т.д.
Отсюда видно соответствие s = jw. Вывод: частотные характеристики могут быть построены по передаточным функциям путем замены s = jw.
Пример: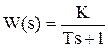 
.
При s = jw имеем:
= 
= 
= 
=
= 
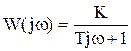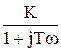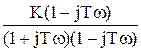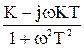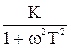- j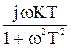 
= Re(w) + j Im(w).
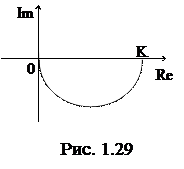
Изменяя w от 0 до ¥, можно построить АФХ (см. рис.). ¨
Для построения АЧХ и ФЧХ используются формулы:
, 
.
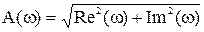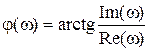Формулы получения АФХ по АЧХ и ФЧХ:
Re(w) = A(w) cos j(w),
Im(w) = A(w) sin j(w).
2.7.2 Логарифмические частотные характеристики.
Логарифмические частотные характеристики (ЛЧХ) используются довольно часто для описания динамических параметров различных устройств. Существуют два основных вида ЛЧХ, которые, как правило, используются совместно и изображаются в виде графиков:
1) ЛАЧХ - логарифмическая АЧХ.
Формула для построения ЛАЧХ: L(w) = 20.lg Aвых(w).
Единица измерения - децибел (дБ).
На графике ЛАЧХ по оси абсцисс откладывается частота в логарифмическом масштабе. Это означает, что равным величинам отрезков по оси w соответствуют кратные значения частоты. Для ЛЧХ кратность = 10.
По оси ординат откладываются значения L(w) в обычном масштабе.
2) ЛФЧХ - логарифмическая ФЧХ. Представляет из себя ФЧХ, у которой ось частоты w проградуирована в логарифмическом масштабе в соответствии с ЛАЧХ. По оси ординат откладываются фазы j.
Примеры ЛЧХ.
1. Фильтр низких частот (ФНЧ)
ЛАЧХ ЛФЧХ Пример цепи
Фильтр низких частот предназначен для подавления высокочастотных воздействий.
2. Фильтр высоких частот (ФВЧ)
ЛАЧХ ЛФЧХ Пример цепи
Фильтр высоких частот предназначен для подавления низкочастотных воздействий.
3. Заградительный фильтр.
Заградительный фильтр подавляет только определенный диапазон частот
ЛАЧХ и ЛФЧХ Пример цепи
 |
.
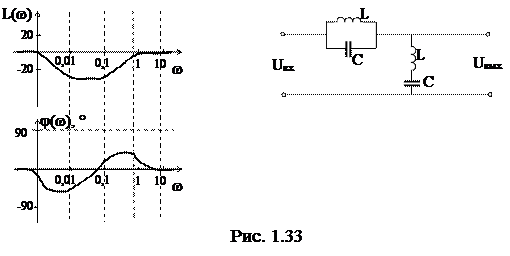3. Качество процессов управления.
3.1. Критерии устойчивости.
3.1.1 Устойчивость.
Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.
Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:
1) корневой критерий,
2) критерий Стодолы,
3) критерий Гурвица,
4) критерий Найквиста,
5) критерий Михайлова и др.
Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.
3.1.2 Корневой критерий.
Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость.
Корни характеристического уравнения могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости (см. рис. 1.34).
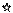(Символом обозначены корни уравнения).
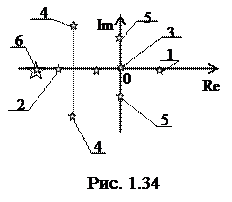Виды корней характеристического уравнения:
- Действительные:
положительные (корень № 1);
отрицательные (2);
нулевые (3);
- Комплексные
комплексные сопряженные (4);
чисто мнимые (5);
По кратности корни бывают:
одиночные (1, 2, 3);
сопряженные (4, 5): si = a ± jw;
кратные (6) si = si+1 = …
Корневой критерий формулируется следующим образом:
Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой.
Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.
Пример 3.1. Передаточная функция системы имеет вид:
.
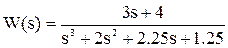Характеристическое уравнение: s3 + 2s2 + 2.25s + 1.25 = 0.
Корни: s1 = -1; s2 = -0,5 + j; s3 = -0,5 - j.
Следовательно, система устойчива. ¨
3.1.3 Критерий Стодолы.
Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.
То есть, для передаточная из примера 3.1 по критерию Стодола соответствует устойчивой системе.
3.1.4 Критерий Гурвица.
Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид (см. рис.)
Wp - передаточная функция регулятора,
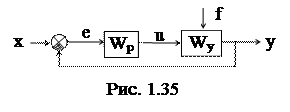Wy - передаточная функция объекта управления.
Определим передаточную функцию для прямой связи (передаточную функцию разомкнутой системы, см. п. 2.6.4): W¥ = Wp Wy.
Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:
.
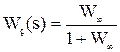Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:
.
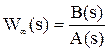Тогда после подстановки и преобразования получаем:
.
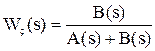Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W¥:
Dз(s) = A(s) + B(s).
Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an+1 по a0. Справа и слева от нее записываются коэффициенты с индексами через 2 (a0, a2, a4… или a1, a3, a5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.
Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.
Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей.
Пример. Дана передаточная функция разомкнутой системы
.
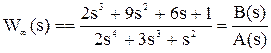Требуется определить устойчивость замкнутой системы по критерию Гурвица.
Для этого определяется ХПЗС:
D(s) = A(s) + B(s) = 2s4 + 3s3 + s2 + 2s3 + 9s2 + 6s + 1 = 2s4 + 5s3 + 10s2 + 6s + 1.
Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1.
Матрица имеет вид:
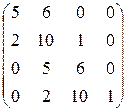
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:
Δ1 = 5 > 0,
,
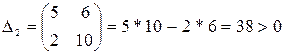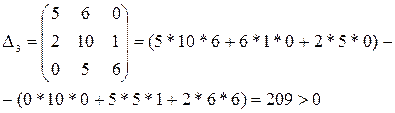
Δ4 = 1* Δ3 = 1*209 > 0.
Поскольку все определители положительны, то АСР устойчива. ♦
3.1.5 Критерий Михайлова.
Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде
,
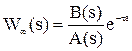где t - запаздывание.
В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.
Порядок применения критерия Михайлова:
1) Записывается характеристическое выражение замкнутой системы:
Dз(s) = A(s) + B(s).e-ts.
2) Подставляется s = jw: Dз(jw) =Re(w) + Im(w).
3) Записывается уравнение годографа Михайлова Dз(jw) и строится кривая на комплексной плоскости.
Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ¥ n квадрантов, где n - степень характеристического полинома.
Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.
3.1.6 Критерий Найквиста.
Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.
Последовательность:
1) Определяется передаточная функция разомкнутой системы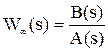 
.
2) Определяется число правых корней m.
3) Подставляется s = jw: W¥(jw).
4) Строится АФХ разомкнутой системы.
Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W¥(jw) m раз охватывала точку (-1; 0), где m - число правых корней разомкнутой системы.
Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.
В случае, если характеристическое уравнение разомкнутой системы A(s) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W¥(jw) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).
3.2. Показатели качества
Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения.
Показатели качества разбиты на 4 группы:
1) прямые - определяемые непосредственно по кривой переходного процесса,
2) корневые - определяемые по корням характеристического полинома,
3) частотные - по частотным характеристикам,
4) интегральные - получаемые путем интегрирования функций.
3.2.1 Прямые показатели качества.
К ним относятся: степень затухания y, перерегулирование s, статическая ошибка ест, время регулирования tp и др.
|
 |
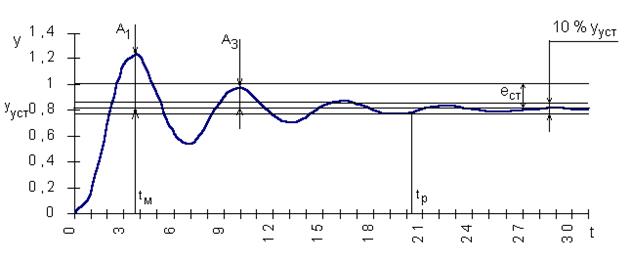Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38).
Сразу по ней определяется установившееся значение выходной величины ууст.
Степень затухания y определяется по формуле
,
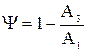где А1 и А3 - соответственно 1-я и 3-я амплитуды переходной кривой.
Перерегулирование s =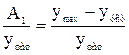 
, где ymax - максимум переходной кривой.
Статическая ошибка ест = х - ууст, где х - входная величина.
Время достижения первого максимума tм определяется по графику.
Время регулирования tp определяется следующим образом: Находится допустимое отклонение D = 5% ууст и строится «трубка» толщиной 2D. Время tp соответствует последней точке пересечения y(t) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
3.2.2 Корневые показатели качества.
К ним относятся: степень колебательности m, степень устойчивости h и др.
Не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:
Степень устойчивости h определяется как граница, правее которой корней нет, т.е.
h = min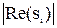 
,
где Re(si) - действительная часть корня si.
Степень колебательности m рассчитывается через угол g: m = tg g. Для определения g проводятся два луча, которые ограничивают все корни на комплексной плоскости. g - угол между этими лучами и мнимой осью. Степень колебательности может быть определена также по формуле:
m = min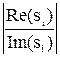 
.
3.2.3 Частотные показатели качества.
Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.
По АФХ определяются запасы: DA - по амплитуде, Dj - по фазе.
Запас DA определяется по точке пересечения АФХ с отрицательной действительной полуосью.
Для определения Dj строится окружность единичного радиуса с центром в начале координат. Запас Dj определяется по точке пересечения с этой окружностью.
По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке МЕ как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.
3.2.4 Связи между показателями качества.
Описанные выше показатели качества связаны между собой определенными соотношениями:
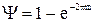; tp = 
; 
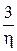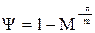; M =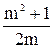 
.
4. Настройка регуляторов.
4.1. Типы регуляторов.
Для регулирования объектами управления, как правило, используют типовые регуляторы, названия которых соответствуют названиям типовых звеньев:
1) П-регулятор (пропорциональный регулятор)
WП(s) = K1.
Принцип действия заключается в том, что он вырабатывает управляющее воздействие на объект пропорционально величине ошибки (чем больше ошибка е, тем больше управляющее воздействие u).
2) И-регулятор (интегрирующий регулятор)
WИ(s) =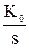 
.
Управляющее воздействие пропорционально интегралу от ошибки.
3) Д-регулятор (дифференцирующий регулятор)
WД(s) = K2 s.
Генерирует управляющее воздействие только при изменении регулируемой веричины:
u = K2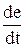 
.
На практике данные простейшие регуляторы комбинируются в регуляторы вида:
4) ПИ-регулятор (пропорционально-интегральный регулятор)
 |
WПИ(s) = K1 + .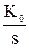
|
5) ПД-регулятор (пропорционально-дифференциальный регулятор)
 |
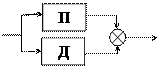WПД(s) = K1 + K2 s.
|
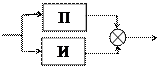
6) ПИД-регулятор.
WПИД(s) = K1 + 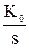+ K2 s.
Наиболее часто используется ПИД-регулятор, поскольку он сочетает в себе достоинства всех трех типовых регуляторов.
4.2. Определение оптимальных настроек регуляторов.
Регулятор, включенный в АСР, может иметь несколько настроек, каждая из которых может изменяться в достаточно широких пределах. При этом при определенных значениях настроек система будет управлять объектом в соответствии с технологическими требованиями, при других может привести к неустойчивому состоянию.
Поэтому стоит задача определить настройки, соответствующие устойчивой системе, но и выбрать из них оптимальные.
Оптимальными настройками регулятора называются настройки, которые соответствуют минимуму (или максимуму) какого-либо показателя качества. Требования к показателям качества устанавливаются непосредственно, исходя из технологических. Чаще всего накладываются требования на время регулирования (минимум) и степень затухания (Y ³ Yзад).
Однако, изменяя настройки таким образом, чтобы увеличить степень затухания, мы можем прийти к слишком большому времени регулирования, что нецелесообразно. И наоборот, стремясь уменьшить время регулирования, мы получаем более колебательные процессы с большим значением Y.
Зависимость Y от tp в общем случае имеет вид, изображенный на графике (см. рис. 1.42).
Поэтому для определения оптимальных настроек разработан ряд математических методов, среди которых метод D-разбиения.
Кривой D-разбиения называется кривая в плоскости настроек регулятора, которая соответствует определенному значению какого-либо показателя качества.
Например, требуется обеспечить степень затухания Y ³ Yзад. Имеется формула, связывающая Y со степенью колебательности m: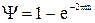 
. Далее строится кривая D-разбиения равной степени колебательности m. Последовательность построения:
1) Определяется ХПЗС Dз(s) с неизвестными настройками.
2) Делается подстановка s = jw - mw и разделение Dз(jw - mw) = Re(w) + Im(w).
3) Полученное выражение приравнивается к нулю и получается система
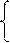Re(w) = 0
Im(w) = 0
Данная система имеет несколько неизвестных: w и настройки регулятора.
4) Далее, изменяя w от 0 до ¥ эта система решается относительно настроек регулятора.
5) По полученным данным строится кривая, по которой определяются оптимальные настройки.
Например, для ПИ-регулятора кривая D-разбиения может иметь вид представленный на рисунке 1.43.
Оптимальные настройки соответствуют максимальному значению K0 (для ПИ- и ПИД-регуляторов) или K1 (для ПД-регулятора).
Часть 2. Средства автоматизации и управления.
1. Измерения технологических параметров.
1.1. Государственная система приборов (ГСП).
ГСП объединяет в себе все средства контроля и регулирования технологических процессов. Характерной особенностью ГСП является:
1) блочно-модульный принцип, лежащий в основе конструкций устройств;
2) унификация входных-выходных сигналов и сигналов питания.
Содержит три ветви:
1) гидравлическую,
2) пневматическую,
3) электрическую.
Блочно-модульный принцип характеризуется наличием отдельных модулей или блоков, выполняющих достаточно простую функцию. Этот принцип позволяет уменьшить номенклатуру средств автоматизации, упрощает ремонт и замену, уменьшает стоимость, позволяет реализовать принцип взаимозаменяемости.
Унифицированные сигналы:
1) Пневматические - сигналы давления сжатого воздуха
диапазон изменения сигнала: 0,2 - 1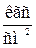 
или 0,02 - 0,1 МПа;
сигнал питания: 1,4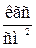 
;
расстояние передачи сигнала: до 300 м.
2) Электрические сигналы имеют много диапазонов, которые можно разделить на две группы:
а) токовые (сигналы постоянного тока), например:
0 - 5 мА, 0 - 20 мА, 4 - 20 мА и др.;
б) сигналы напряжения постоянного тока, например: 0 - 1 В, 0 - 10 В и др.
Первичные приборы (датчики) могут преобразовывать измеряемый параметр в какой-либо унифицированный сигнал. Если же датчик выдает неунифицированный сигнал, то для приведения его к стандартному диапазону должен быть установлен соответствующий преобразователь.
1.2. Точность преобразования информации.
Прямое измерение – измерение, при котором искомое значение величины находят непосредственно из опытных данных.
Косвенное измерение - измерение, при котором искомое значение величины находят на основании зависимости между этой величиной и величинами, подвергаемыми, прямым измерениям.
Принцип измерений – совокупность физических явлений, на которых основаны измерения.
Метод измерений – совокупность приемов использования принципов и средств измерений.
Средство измерений – техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства.
Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.
Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем.
Аналоговый измерительный прибор – измерительный прибор, показания которого являются непрерывной функцией изменений измеряемой величины.
Цифровой измерительный прибор – измерительный прибор, автоматически вырабатывающий дискретные сигналы измерительной информации, показания которого представлены в цифровой форме.
Показывающий измерительный прибор – измерительный прибор, допускающий только отсчитывание показаний.
Показания средства измерений – измерение величины, определяемое по отсчетному устройству и выраженное в принятых единицах этой величины.
Градуировочная характеристика средства измерений – зависимость между значениями величин на выходе и входе средства измерений, составленная в виде таблицы, графика или формулы.
Диапазон показаний – область значений шкалы, ограниченная конечны и начальным значениями шкалы.
Диапазон измерений – область значений измеряемой величины, для которой нормированы допускаемые погрешности средства измерений.
Предел измерений – наибольшее и наименьшее значения диапазона измерений.
Чувствительность измерительного прибора – отношение изменения сигнала на выходе измерительного прибора к вызывающему его изменению измеряемой величины.
Любые измерения сопровождаются погрешностями:
1) случайные погрешности - имеют случайную природу и причина их неизвестна;
2) промахи - вызваны неправильными отсчетами по прибору;
3) систематические - обусловлены несовершенством методов определения, конструкции прибора.
Виды погрешностей:
1) абсолютные: DХ = Х - Х0,
где Х - измеренное значение параметра, Х0 - истинное значение;
Абсолютная погрешность измерения – погрешность измерения, выраженная в единицах измеряемой величины.
2) относительные: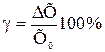 
(выраженные в %-ах);
Относительная погрешность измерения – отношение абсолютной погрешности измерения к истинному значению измеряемой величины. Относительная погрешность может быть выражена в процентах.
3) приведенные: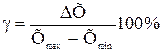 
,
где Хmin и Хmax - минимальное и максимальное значения измеряемой величины.
Максимальная приведенная погрешность называется классом точности:
.
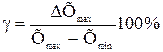В зависимости от класса точности приборы делятся на эталонные (образцовые) и рабочие.
1.3. Классификация КИП.
На нефтеперерабатывающих и химических производствах наиболее часто измеряемыми величинами являются температура, давление, расход и уровень. На них приходится около 80 % всех измерений. Остальную часть занимают электрические, оптические и др. измерения.
При измерениях используются различные измерительные приборы, которые классифицируются по ряду признаков. Общей градацией является разделение их на приборы для измерения: механических, электрических, магнитных, тепловых и других физических величин.
Классификация по роду измеряемой величины указывает, какую физическую величину измеряет прибор (давление Р, температуру Т, расход F, уровень L, количество вещества Q и т.д.).
Исходя из признака преобразования измеряемой величины, измерительные приборы разделяют на приборы:
а) непосредственной оценки;
б) сравнения.
По характеру измерения: стационарные и переносные.
По способу отсчета измеряемой величины: показывающие, регистрирующие, суммирующие.
1.4. Виды первичных преобразователей.
Первичные приборы или первичные преобразователи предназначены для непосредственного преобразования измеряемой величины в другую величину, удобную для измерения или использования. Различают генераторные, параметрические и механические преобразователи:
1) Генераторные осуществляют преобразование различных видов энергии в электрическую, то есть они генерируют электрическую энергию (термоэлектрические, пьезоэлектрические, электрокинетические, гальванические и др. датчики).
2) К параметрическим относятся реостатные, тензодатчики, термосопротивления и т.п. Им для работы необходим источник энергии.
3) Выходным сигналом механических первичных преобразователей (мембранных, манометров, дифманометров, ротаметров и др.) является усилие, развиваемое чувствительным элементом под действием измеряемой величины.
1.5. Методы и приборы для измерения температуры.
1.5.1 Классификация термометров.
Температура вещества - величина, характеризующая степень нагретости, которая определяется внутренней кинетической энергией теплового движения молекул. Измерение температуры практически возможно только методом сравнения степени нагретости двух тел.
Для сравнения нагретости этих тел используют изменения каких-либо физических свойств, зависящих от температуры и легко поддающихся измерению.
По свойству термодинамического тела, используемого для измерения температуры, можно выделить следующие типы термометров:
· термометры расширения, основанные на свойстве температурного расширения жидких тел;
· термометры расширения, основанные на свойстве температурного расширения твердых тел;
· термометры газовые манометрические;
· термометры жидкостные манометрические;
· конденсационные;
· электрические;
· термометры сопротивления;
· оптические монохроматические пирометры;
· оптические цветовые пирометры;
· радиационные пирометры.
1.5.2 Термометры расширения. Жидкостные стеклянные.
Тепловое расширение жидкости характеризуется сравнительным коэффициентом объемного расширения, значение которого определяется как
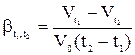, 1/град,
где V0, Vt1, Vt2 - объемы жидкости при 0 °С, температурах t1 и t2 соответственно.
Чувствительность термометра зависит от разности коэффициентов объемного расширения термометрической жидкости и стекла, от объема резервуара и диаметра капилляра. Чувствительность термометра обычно лежит в пределах 0,4…5 мм/°С (для некоторых специальных термометров 100…200 мм/°С).
Для защиты от повреждений технические термометры монтируются в металлической оправе, а нижняя погружная часть закрывается металлической гильзой.
1.5.3 Термометры, основанные на расширении твердых тел.
К этой группе приборов относятся дилатометрические и биметаллические термометры, основанные на изменении линейных размеров твердых тел с изменением температуры.
1) Конструктивное исполнение дилатометрических термометров основано на преобразовании измеряемой температуры в разность абсолютных значений удлинений двух стержней, изготовленных из материалов с существенно различными термическими коэффициентами линейного расширения:
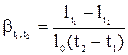, 1/град,
где l0, lt1, lt2 - линейные размеры тела при 0 °С, температурах t1 и t2 соответственно.
В силу того, что Db мала, дилатометрические термометры применяются в качестве различного рода тепловых реле в устройствах сигнализации и регулирования температуры.
2) Биметаллические термометры основаны на деформации биметаллической ленты при изменении температуры. Обычно применяются биметаллические ленты, согнутые в виде плоской или винтовой спирали. Один конец спирали укреплен неподвижно, второй - на оси стрелки. Угол поворота стрелки равен углу закручивания спирали, который пропорционален изменению температуры.
Биметаллические термометры обеспечивают изменение температуры с относительными погрешностями 1 - 1,5 %.
1.5.4 Газовые манометрические термометры.
В основу принципа действия манометрического термометра положена зависимость между температурой и давлением термометрического (рабочего) вещества, лишенного возможности свободно расширяться при нагревании.
Манометрические термометры обычно включают в себя термобаллон, капиллярную трубку и трубчатую пружину с поводком, зубчатым сектором и стрелкой. Вся стистема заполняется рабочим веществом. При нагревании термобаллона, установленного в зоне измеряемой температуры, давление рабочего вещества внутри замкнутой системы увеличивается. Увеличение давления воспринимается манометрической пружиной, которая воздействует через передаточный механизм на стрелку или перо прибора.
Газовые манометрические термометры основаны на зависимости температуры и давления газа, заключенного в герметически замкнутой термосистеме.
Достоинства: шкала прибора практически равномерна.
Недостатки: сравнительно большая инерционность и большие размеры термобаллона.
1.5.5 Жидкостные манометрические термометры.
В качестве манометрической жидкости в приборах этого типа применяется метиловый спирт , ксилол, толуол, ртуть и т.д.
Жидкостные манометрические термометры имеют равномерную шкалу.
1.5.6 Конденсационные манометрические термометры.
Конденсационные манометрические термометры реализуют зависимость упругости насыщенных паров низкокипящей жидкости от температуры. Поскольку эти зависимости для используемых жидкостей (хлористый метил, этиловый эфир, хлористый этил, ацетон и др.) нелинейны, следовательно, и шкалы термометров неравномерны. Однако, эти приборы обладают более высокой чувствительностью, чем газовые жидкостные.
1.5.7 Электрические термометры.
Принцип действия этого типа термометров основан на зависимости термо-ЭДС (ТЭДС) цепи от изменения температуры.
В термоэлектрической цепи, состоящей из двух проводников А и В (см. рис. 2.1) возникают 4 различные ТЭДС: 2 ТЭДС в местах спаев проводников А и В, ТЭДС на конце проводника А и ТЭДС на конце проводника В. Суммарная ТЭДС, возникающая при нагреве спаев проводников до температур t и t0:
EAB(t t0) = eAB(t) + eBA(t0),
где eBA и eAB - ТЭДС, обусловленная контактной разностью потенциалов и разностью температур концов А и В.
ТЭДС EAB(t t0) является функцией от температуры горячего спая t при условии постоянства температуры холодного спая t0.
Термопары градуируются при определенной постоянной температуры t0 (обычно t0 = 0 °C или 20 °C). При измерениях температура t0 может отличаться от градуировочного значения. В этом случае вводится соответствующая поправка в результат измерения:
EAB(t t0) = EAB(t t0’) + EAB(t0’t0).
Поправка EAB(t0’t0) равна ТЭДС, которую развивает данная термопара при температуре горячего спая t0’ и градуировочном значении температуры холодных спаев. Поправка берется положительной, если t0’ > t0 и отрицательной, если t0’ < t0.
Величина поправки может быть взята из градуировочной таблицы.
Конструктивное исполнение термопар разнообразно и зависит главным образом от условий их применения. При необходимости измерения небольшой разницы температур или получения большой ТЭДС применяются дифференциальные термопары и термобатареи, представляющие собой несколько последовательно соединенных термопар.
Компенсация изменения температуры холодных спаев термопар. Правильное измерение температуры возможно лишь при постоянстве температур свободных спаев t0. Оно обеспечивается с помощью соединительных проводов и специальных термостатирующих устройств. Соединительные провода в данном случае предназначены для переноса свободных концов термопары в зону с известной постоянной температурой, а также для подсоединения свободных концов термопары к зажимам измерительных приборов. Соединительные провода должны быть термоэлектрически подобны термоэлектродам термопары.
Как правило, соединительные провода для термопар, изготовленных из неблагородных металлов, выполняются из тех же самых материалов, что и термоэлектроды. Исключение составляет хромель-алюмелевая термопара, для которой с целью уменьшения сопротивления линии в качестве соединительных проводов применяется медь в паре с константаном.
Градуировки термопар: ХА - хромель-алюмелевые; ХК - хромель-копелевые;
ПП - платинородий-платиновые и т.д.
Требования к термопарам:
1) воспроизводимость,
2) высокая чувствительность,
3) надежность,
4) стабильность,
5) достаточный температурный диапазон.
Таблица 2.1 - Материалы, используемые для изготовления термопар.
| Название | Состав | ТЭДС, мВ (при t0 = 0 °C и t1 = 100 °C) | Максимальный темпер. предел, °C |
| хромель | 10% Cr + 90 % Ni | +2,95 | 1000 |
| платинородий | 90 % Pt + 10 % Rh | +0,86 | 1300 |
| медь | Cu | +0,76 | 350 |
| платина | Pt | 0 | 1300 |
| алюмель | 95 % Ni + 5 % Al | -1,2 | 1000 |
| копель | 56 % Cu + 44 % Ni | -4 | 600 |
| константан | 60 % Cu + 40 % Ni | -3,4 | 600 |
Методы и средства для измерения ТЭДС:
1) Метод непосредственной оценки ( с помощью милливольтметра);
2) Компенсационный метод (с помощью потенциометров).
1.5.8 Термометры сопротивления.
Измерение температуры термосопротивлениями основано на свойстве проводников и полупроводников изменять свое электрическое сопротивление при изменении температуры.
Вид функции R = f(t) зависит от природы материала. Для изготовления чувствительных элементов серийных термосопротивлений применяются чистые металлы, к которым предъявляются следующие требования:
а) металл не должен окисляться или вступать в химические реакции с измеряемой средой;
б) температурный коэффициент электрического сопротивления металла a должен быть достаточно большим и неизменным;
в) функция R = f(t) должна быть однозначна.
Наиболее полно указанным требованиям отвечают: платина, медь, никель, железо и др.
Основной недостаток термосопротивлений: большая инерционность (до 10 мин.).
Для измерения температуры наиболее часто применяются термосопротивления типов ТСП (платиновые) и ТСМ (медные).
1.5.9 Пирометры излучения.
Пирометры излучения основаны на использовании теплового излучения нагретых тел. Верхний предел измерения температуры пирометра излучения практически не ограничен. Измерение основано на бесконтактном способе, поэтому отсутствует искажение температурного поля, вызываемого введением преобразовательного элемента прибора в измеряемую среду. Возможно измерение температуры пламени и высоких температур газовых потоков при больших скоростях.
Лучистая энергия выделяется нагретым телом в виде волн различной длины. При сравнительно низких температурах (до 500 °С) нагретое тело испускает инфракрасные лучи. По мере повышения температуры цвет тела от темно-красного доходит до белого. Возрастание интенсивности монохроматического излучения с повышением температуры описывается соответствующими уравнениями.
1.5.10 Цветовые пирометры.
В цветовых пирометрах определяется отношение интенсивности излучения реального тела Еl в лучах с двумя заранее выбранными значениями длины волны l1 и l2, то есть показания цветовых пирометров определяется функцией f(Еl1 / Еl2). Это отношение для каждой температуры различно, но однозначно.
1.6. Вторичные приборы для измерения разности потенциалов.
Для измерения ТЭДС в комплектах термоэлектрических термометров применяются пирометрические милливольтметры и потенциометры. В потенциометрах, в отличие от милливольтметров, используется компенсационный метод измерения.
1.6.1 Пирометрические милливольтметры.
Пирометрические милливольтметры являются электро-измерительными приборами магнито-электрической системы.
В конструкции пирометрических милливольтметров можно выделить магнитную и подвижную системы. Первая состоит из подковообразного магнита 1, полюсных наконечников 2 и цилиндрического сердечника 3. Кольцевой зазор между сердечником и полюсными наконечниками характеризуется наличием практически равномерного электромагнитного поля.
В этом зазоре соосно с сердечником размещается рамка 4, которая монтируется на кернах, опирающихся на подпятники, либо на натянутых нитях. Момент сил, противодействующий вращению рамки создается специальными пружинами.
Взаимодействие тока, протекающего по рамке с полем постоянного магнита 2 вызывает появление вращающего момента, который, будучи уравновешен противодействующим моментом пружин, поворачивает рамку на определенный угол. Этот угол пропорционален величине протекающего по рамке тока.
1.6.2 Потенциометры.
|
|
|
Потенциометры в отличие от милливольтметров работают по компенсационному (нулевому) методу измерения.
|
|
|
Принцип компенсации при измерении ТЭДС заключается в уравновешивании ее известным напряжением DU на калибровочном резисторе RАВ, созданным вспомогательным источником тока. Ток от вспомогательного источника проходит через реохорд RAB.UAB пропорционально RАВ (в точке D находится движок реохорда).
|
1.6.3 Автоматические электрические потенциометры.
Схема автоматического потенциометра показана на рис. 2.5, где обозначено:
Rp - сопротивление реохорда,
Rш - шунта,
Rп - для задания пределов измерения,
Rн и Rк - для задания начала и конца шкалы,
Rб - балластное,
Rс - для поверки рабочего тока,
Rм - медное сопротивление для компенсации влияния температуры холодных спаев.
ИПС - источник питания стабилизированный.
Потенциометр состоит из моста сопротивлений АВСD, в одну из диагоналей которого включен источник питания ИПС (диагональ ВС), а в другую (измерительную диагональ АD) термопара с ТЭДС Е и электродвигатель ЭД с усилителем УЭД. В вершине А моста находится реохорд Rр, к движку которого прикреплена стрелка, движущаяся вдоль шкалы. Перемещением движка в свою очередь управляет электродвигатель.
Мост может находится в двух состояниях: уравновешенном и неуравновешенном.
Когда мост находится в равновесии, то напряжение между его вершинами AD равно по модулю термоЭДС (UAD = Е) и напряжение небаланса ΔU, подаваемое на усилитель УЭД, равно нулю:
ΔU = UAD – Е = 0.
В данном состоянии ЭД не работает.
Если по каким-либо причинам термо-ЭДС Е изменится, то мост выходит из равновесия и на входе усилителя УЭД появится напряжение небаланса ΔU ≠ 0. Усилитель, усилив напряжение, подает его на ЭД, который, вращаясь, перемещает движок реохорда. перемещение движка продолжается до тех пор, пока мост снова не придет в равновесие и напряжение на ЭД снова не станет равно нулю.
В этих потенциометрах процесс компенсации осуществляется автоматически, непрерывно и с большой скоростью. Эти приборы имеют устройства для автоматического внесения поправки на температуру холодных спаев термопары.
1.7. Методы измерения сопротивления.
Для измерения сопротивлений термоэлектрических сопротивлений (ТС) часто используют автоматические электронные мосты, включенные по двухпроводной, трехпроводной или четырехпроводной схемам.
Двухпроводная схема подключения моста к ТС показана на рис. 2.6, где обозначены:
R1, R2, R3, R4 - сопротивления моста;
Rб - балластное сопротивление для ограничения рабочего тока;
Rт - сопротивление ТС;
Rл - сопротивление линии (соединительных проводов).
Условием равновесия моста является равенство произведений противолежащих плечей, т.е. в данном случае:
R1.R3 » R2.(R4 + Rт + 2.Rл).
Когда мост уравновешен, напряжение на диагонали UAD = 0 и, следовательно, ЭД не работает. При изменении температуры объекта изменяется Rт и UAD перестает быть нулевым. Это напряжение усиливается УЭД и подается на ЭД, который, вращаясь, перемещает движок реохорда.
Недостатком такой схемы является то, что сопротивления линии входят в одно плечо с Rт, следовательно, изменение Rл может вызывать изменение показаний моста. Для компенсации Rл применяются трехпроводная или четырехпроводная схемы.
Трехпроводная схема подключения моста (см. рис. 2.7).
В этом случае уравнение равновесия имеет вид:
(R1 + Rл).R3 » R2.(R4 + Rт + Rл).
То есть сопротивление линии Rл входит в обе части уравнения и частично компенсируется.
1.8. Методы и приборы для измерения давления и разряжения.
1.8.1 Классификация приборов для измерения давления.
Под давлением в общем случае понимают предел отношения нормальной составляющей усилия к площади, на которую действует усилие.
В зависимости от природы контролируемого процесса нас интересует абсолютное давление Ра или избыточное Ри. При измерении Ра за начало отсчета принимается нулевое давление, которое можно себе представить как давление внутри сосуда после полной откачки воздуха. Естественно, достигнуть Ра = 0 невозможно.
Барометрическое давление Рбар - давление, оказываемое атмосферой на все находящиеся в ней предметы.
Избыточное давление представляет собой разность между абсолютным и барометрическим давлениями:
Ри = Ра - Рбар
Если Рабс < Рбар, то Ри называется давлением разряжения.
Классификация приборов для измерения давления:
I . По принципу действия:
1) жидкостные (основанные на уравновешивании давления столбом жидкости);
2) поршневые (измеряемое давление уравновешивается внешней силой, действующей на поршень);
3) пружинные (давление измеряется по величине деформации упругого элемента);
4) электрические (основанные на преобразовании давления в какую-либо электрическую величину).
II . По роду измеряемой величины:
1) манометры (измерение избыточного давления);
2) вакуумметры (измерение давления разряжения);
3) мановакуумметры (измерение как избыточного давления, так и давления разряжения);
4) напорометры (для измерения малых избыточных давлений);
5) тягомеры (для измерения малых давлений разряжения);
6) тягонапорометры;
7) дифманометры (для измерения разности давлений);
8) барометры (для измерения барометрического давления).
1.8.2 Жидкостные манометры.
Широко применяются в качестве образцовых приборов для лабораторных и технических измерений. В качестве рабочей жидкости используется спирт, вода, ртуть, масла.
Двухтрубный манометр представляет из себя U-образную трубку, заполненную затворной жидкостью.
1.8.3 Чашечные манометры и дифманометры.
|
Уравнение равновесия: Р = r g (h + H).
|
1.8.4 Микроманометры.
|
Применяются для измерения давлений, меньших 100 - 200 мм водяного столба. Представляют из себя жидкостной манометр с наклоненной по углом 20…50° трубкой.
h = L.sin(a) - высота поднятия уровня жидкости в узкой трубке,
P = r.g.h - измеренное давление.
Погрешность: ± 1,5 %.
1.8.5 Пружинные манометры.
Состоят из трубчатой пружины 1 с поводком, зубчатого сектора 3 и шестерни 4 с прикрепленной к ней стрелкой 2.
При увеличении давления трубчатая пружина стремится разогнуться, в результате чего она через поводок начинает взаимодействовать на зубчатый сектор, отклоняя стрелку.
1.8.6 Электрические манометры.
Преобразователи давления типа "Сапфир".
Эти манометры обеспечивают непрерывное преобразование значение измеряемого параметра (давления избыточного, абсолютного, разряжения, разности давлений нейтральных и агрессивных сред) в унифицированный токовый сигнал для дистанционной передачи (0 - 5 мА, 0 - 20 мА и др.).
Мембранный тензопреобразователь 3 размещен внутри основания 9 (см. рис. 2.13). Внутренняя полость 4 тензопреобразователя заполнена кремнийорганической жидкостью и отделена от измеряемой среды металлической гофрированной мембраной 6, приваренной по наружному контуру к основанию 9. Полость 10 сообщена с окружающей атмосферой.
Измеряемое давление подается в камеру 7 фланца 5, который уплотнен прокладкой 8. Измеряемое давление воздействует на мембрану 6 и через жидкость воздействует на мембрану тензопреобразователя, вызывая ее прогиб и изменение сопротивления тензорезисторов. Электрический сигнал от тензопреобразователя передается из измерительного блока 1 по проводам через гермовывод 2.
Преобразователи Сапфир-22ДА моделей 2050 и 2060, предназначенные для измерения абсолютного давления, отличаются тем, что полость 10 вакуумирована и герметизирована.
Преобразователи Сапфир-22ДД моделей 2410, 2420, 2430, 2434, 2440 и 2444 (см. рис. 2.14), предназначенные для измерения разности давлений, отличаются тем, что в них используется тензопреобразователь мембранно-рычажного типа, который размещен внутри основания в замкнутой полости, заполненной кремнийорганической жидкостью, и отделен от измеряемой среды двумя металлическими гофрированными мембранами. Мембраны соединены между собой центральным штоком, перемещение которого передается рычагу тензопреобразователя, что вызывает деформацию тензопреобразователя. Чувствительным элементом тензопреобразователя является пластина из монокристаллического сапфира (разновидность корунда - Al2O3) с кремниевыми пленочными тензорезисторами (структура КНС - кремний на сапфире).
|
Электрический сигнал от тензопреобразователя передается из измерительного блока в электронное устройство 1 по проводам через гермоввод 2. Измерительный блок выдерживает без разрушения воздействие односторонней перегрузки рабочим избыточным давлением. Это обеспечивается тем, что при такой перегрузке одна из мембран 8 ложится на профилированную поверхность основания 9.
1.9. Методы и приборы для измерения расхода пара, газа и жидкости.
1.9.1 Классификация.
Количество вещества выражается в единицах объема или массы (т.е. в м3 или килограммах). Количество жидкости с равной степенью точности может быть измерено и объемным, и массовым методами, количество газа - только объемным. Для твердых и сыпучих материалов используется понятие насыпной или объемной массы, которая зависит от гранулометрического состава сыпучего материала. Для более точных измерений количество сыпучего материала определяется взвешиванием.
Расходом вещества называется количество вещества, проходящее через данное сечение трубопровода в единицу времени. Массовый расход измеряется в кг/с, объемный - в м3/с.
Приборы, измеряющие расход, называются расходомерами. Эти приборы могут быть снабжены счетчиками (интеграторами), тогда они называются расходомерами-счетчиками. Такие приборы позволяют измерять расход и количество вещества.
Классификация:
Механические
объемные
ковшовые
барабанного типа
мерники
скоростные
по методу переменного перепада давления
по методу постоянного перепада давления
напорные трубки
ротационные
Электрические
электромагнитные
ультразвуковые
радиоактивные
1.9.2 Метод переменного перепада давления.
Является самым распространенным и изученным методом измерения расхода жидкости, пара и газа.
В измерительной технике сужающими устройствами являются диафрагмы, сопла и сопла Вентури.
Наиболее часто из них применяются диафрагмы, которые представляют собой тонкий диск, установленный в трубопроводе так, чтобы его отверстие было концентрично внутреннему контуру сечения трубопровода. Сужение потока начинается до диафрагмы. Затем на некотором расстоянии за ней благодаря действию сил инерции, поток сужается до минимального значения, а далее постепенно расширяется до полного сечения трубопровода. Перед диафрагмой и за ней образуются зоны с вихревым движением.
I - I - сечение потока до искажения формы.
II - II - сечение в месте максимального сужения.
Рп - потери давления на трение и завихрения.
Разность давлений Р1 - Р2 зависит от расхода среды, протекающей через трубопровод.
В случае использования сопла струя, протекающая через него, не отрывается от его профилированной части и поэтому Рп меньше.
Еще меньше потери Рп в сопле Вентури.
Перепад давления измеряется дифманометрами. Комплект расходомера состоит из элементов:
1) сужающее устройство (Д);
2) импульсные трубки (Т);
3) дифманометр (ДМ).
В качестве дифманометров обычно используются преобразователи разности давлений типа "Сапфир".
1.9.3 Расходомеры постоянного перепада давления.
К ним относятся гидродинамические, поршневые, поплавковые, ротаметрические расходомеры.
Наиболее распространенными приборами группы расходомеров постоянного перепада давления являются ротаметры (см. рис. 2.17), которые имеют ряд преимуществ перед расходометрами переменного перепада давления:
а) потери Рп незначительны и не зависят от расхода;
б) имеют большой диапазон измерения и позволяют измерять малые расходы.
Принцип действия основан на измерении положения Н поплавка, вращающегося в расширяющейся кверху трубке под влиянием направленной вверх струи.
Q - расход проходящего через трубку газа или жидкости,
a - угол наклона стенок трубки.
Зависимость Н от Q нелинейна, но в начальном и среднем участках равномерность делений шкалы искажается в незначительной степени.
Отсутствие прямой зависимости между Q и Н требует индивидуальной градуировки каждого прибора.
Ротаметрические трубки обычно изготавливаются из стекла, на которое наносится шкала. Ротор также может быть изготовлен в виде шарика или диска.
1.9.4 Расходомеры переменного уровня.
Используются для измерения расходов смесей продуктов, содержащих твердые частицы, пульсирующих потоков, особо активных сред.
Измерения осуществляются при атмосферном давлении. Состоит из элементов (см. рис. 2.18): 1 - калиброванный сосуд, 2 - уровнемерное стекло, 3 - отверстие в днище, 4 - перегородка для успокоения потока.
1.9.5 Расходомеры скоростного напора.
Измерение расхода основано на зависимости динамического напора от скорости потока измеряемой среды.
Дифманометр, соединяющий обе трубки, показывает динамическое давление, по котором судят о скорости потока и, следовательно, о расходе.
1.10. Методы и приборы для измерения уровня.
1.10.1 Методы измерения уровня.
В общем объеме измерительных операций в нефтепереработке, нефтехимии и газовой промышленности измерение уровня составляет 18 - 20 %.
Поl измерением уровня понимается индикация положения раздела двух сред различной плотности относительно какой-либо горизонтальной поверхности, принятой за начало отсчета. Приборы, выполняющие эту задачу, называются уровнемерами.
Методы измерения уровня: 1) поплавковый, 2) буйковый, 3) гидростатический, электрические и др.
1.10.2 Поплавковый метод измерения уровня.
Поплавковый уровнемер построен по принципу использования выталкивающей силы жидкости. Чувствительный элемент представляет собой тело произвольной формы (поплавок), плавающий на поверхности жидкости и имеющий постоянную осадку. Поплавок перемещается вертикально вместе с уровнем жидкости и текущее значение уровня определяется фиксацией положения поплавка.
1.10.3 Буйковые уровнемеры.
Действие буйкового уровнемера основано на законе Архимеда. Чувствительный элемент буйкового уровнемера - буй - массивное тело, подвешенное вертикально внутри сосуда, уровень жидкости в котором контролируется. По мере изменения уровня жидкости изменяется погружение буя вследствии компенсации выталкивающей силы жидкости изменением усилия в подвеске.
Таким образом, по величине погружения буя судят об уровне жидкости в сосуде. Характеристика буйкового уровнемера линейная, а чувствительность тем больше, чем больше площадь поперечного сечения буя.
1.10.4 Гидростатические уровнемеры.
В этих приборах измерение уровня жидкости постоянной плотности сводится к измерению давления, созданного столбом жидкости Р = rж g h.
Различают пьезометрические уровнемеры и уровнемеры с непосредственным измерением столба жидкости.
Пьезометрические уровнемеры применяются для измерения уровня самых разнообразных, в том числе вязких и агрессивных жидкостей.
Воздух из пьезометрической трубки 1 барботирует через слой жидкости. Количество воздуха, подаваемого под давлением, ограничивается дросселем 3 таким образом, чтобы скорость движения его в трубопроводе была минимально возможной. Уровень жидкости определяется по разности давления в дифманометре 2.
1.10.5 Электрические методы измерения уровня.
Для измерения уровня жидкости может быть использовано различие электрических свойств жидкости и парогазовой смеси под ней. Под электрическими свойствами понимаются диэлектрическая проницаемость и электропроводность веществ.
Кондуктометрический метод измерения уровня основан на измерении электрической проводимости первичного преобразователя, зависящей от значения уровня.
Емкостной метод измерения основан на изменении емкости первичного преобразователя в зависимости от положения уровня измеряемой среды. Обычно первичный преобразователь выполняется в виде коаксиальных цилиндрических обкладок, погруженных в измеряемую жидкость. С изменением уровня жидкость заполняет пространство между обкладками и тем самым изменяет их электрическую емкость. Зависимость между уровнем жидкости и емкостью пропорциональная.
2. Исполнительные устройства.
2.1. Классификация исполнительных устройств.
Исполнительным устройством (ИУ) называется устройство в системе управления, непосредственно реализующее управляющее воздействие со стороны регулятора на объект управления путем механического перемещения регулирующего органа (РО) объекта.
Большинство управляющих воздействий в нефтепереработке, нефтедобыче и нефтехимии реализуется путем изменения расходов веществ (например, сырья, топлива, кубового остатка колонны и т.д.).
Уравнение статики ИУ для расхода F жидкости или газа может быть описано как
F = F(ΔP, ν, ρ, C1, C2, …),
где ΔP – перепад давления на РО, ν - вязкость, ρ – плотность, Сi – некоторые параметры, зависящие от конструкции РО, режима истечения потока и т.д. Отсюда видно, что расход F может быть изменен путем:
- изменения ΔP (насосные ИУ),
- ν или ρ (реологические ИУ),
- коэффициентами Ci (дроссельные ИУ).
Примеры схем контроля давления.
Индикация давления ( PI ).
210-1 Манометр пружинный М-… (см. рис. 2.36)
Литература
1. Кулаков М.В. Технические измерения и приборы для химических производств. М.: Машиностроение, 1983. - 424 с.
2. Никитенко Е.А. автоматизация и телеконтроль электрохимической защитой магистральных газопроводов. М.: Недра, 1976.
3. Полоцкий Л.М., Лапшенков Г.И. Автоматизация химических производств. Учеб. пособ. -М.: Химия, 1982. - 296 с.
4. Теория автоматического управления / Под ред. Нетушила А.В. Ч.1. -М.: Высш. шк., 1968.
5. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. -М.: Наука, 1966.
6. Дадаян Л.Г. Автоматизация технологических процессов: методические указания к курсовому и дипломному проектированию. -Уфа.: Изд-во УНИ, 1985. - 225 с.
7. Камразе А.Н., Фитерман М.Я. Контрольно-измерительные приборы и автоматика. Л.: Химия, 1988. - 225 с.
8. Стефани Е.П. Основы построения АСУТП: Учеб. пособ. -М.: Энергоиздат, 1982. -352 с.
9. Автоматические приборы, регуляторы и управляющие машины: Справочник /Под ред. Кошарского Б.Д. -Изд. 3-е. -Л.: Машиностроение, 1976. -486 с.
10. Голубятников В.А., Шувалов В.В. Автоматизация производственных процессов в химической промышленности: Учебник. -М.: Химия, 1985. -352 с.
11. Теория автоматического управления: Учебник. В 2-х частях / Под ред. А.А.Воронова. -М.: Высш.шк., 1986. -Ч.1. - 367 с. - Ч.2. -504 с.
12. Аязян Г.К. Расчет автоматических систем с типовыми алгоритмами регулирования: Учеб. пособ. -Уфа.: Изд-во УНИ, 1986. -135 с.
13. Веревкин А.П., Попков В.Ф. Технические средства автоматизации. Исполнительные устройства: Учеб. пособ. -Уфа.: Изд-во УНИ, 1996. -95 с.
14. ГОСТ 21.404-85. Обозначения условные приборов и средств автоматизации.
15. ГОСТ 21.408-93. Правила выполнения рабочей документации автоматизации технологических процессов.
16. Кузнецов А. SCADA-системы: программистом можешь ты не быть.// СТА. -1996. -№ 1. –С. 32 – 35.
17. Кабаев С. SCADA-пакет InTouch в отечественных проектах.// Мир компьютерной автоматизации. -1997. -№ 2. – С. 88 – 90.
18. Христенсен Д. Знакомство со стандартом на языки программирования PLC IEC 1131-3.// Мир компьютерной автоматизации. -1997. -№ 2. – С. 24 – 25.
СОДЕРЖАНИЕ
С.
Управление техническими системами
курс лекций
Уфа 2003
УДК 658.012 (07)
ББК 32.965я7
К 43
Рецензенты: директор Регионального центра тестирования, канд. техн. наук,
доцент Ахметсафина Р.З.;
зав. кафедрой АПП, канд. техн. наук, доцент Сафонов В.В.
К 43 Кирюшин О.В. Управление техническими системами: курс лекций. –
Уфа: Изд-во УГНТУ, 2003. – 80 с.
Учебное пособие написано по материалам курса «Управление техническими системами», читаемого на кафедре Автоматизации химико-технологических процессов УГНТУ для студентов различных специальностей.
Изложенный материал разделен на три части:
1) теория автоматического управления, в которой содержатся теоретические основы построения систем управления;
2) средства автоматизации и управления, где описываются основные методы измерения и средства автоматизации, используемые в нефтедобыче, нефтепереработке и нефтехимии;
3) современные системы управления производством, где вкратце перечислены основные аспекты построения АСУ ТП.
Ó Уфимский государственный нефтяной технический университет, 2003
Ó Кирюшин О.В., 2003
Часть 1. Теория Автоматического Управления (ТАУ)
1. Основные термины и определения ТАУ.
1.1. Основные понятия.
Системы управления современными химико-технологическими процессами характеризуются большим количеством технологических параметров, число которых может достигать нескольких тысяч. Для поддержания требуемого режима работы, а в конечном итоге – качества выпускаемой продукции, все эти величины необходимо поддерживать постоянными или изменять по определенному закону.
Физические величины, определяющие ход технологического процесса, называются параметрами технологического процесса. Например, параметрами технологического процесса могут быть: температура, давление, расход, напряжение и т.д.
Параметр технологического процесса, который необходимо поддерживать постоянным или изменять по определенному закону, называется регулируемой величиной или регулируемым параметром.
Значение регулируемой величины в рассматриваемый момент времени называется мгновенным значением.
Значение регулируемой величины, полученное в рассматриваемый момент времени на основании данных некоторого измерительного прибора называется ее измеренным значением.
Пример 1. Схема ручного регулирования температуры сушильного шкафа.
 |
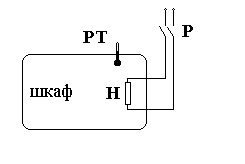Рис. 1.1
Требуется вручную поддерживать температуру в сушильном шкафу на уровне Тзад.
Человек-оператор в зависимости от показаний ртутного термометра РТ включает или выключает нагревательный элемент Н с помощью рубильника Р. ¨
На основе данного примера можно ввести определения:
Объект управления (объект регулирования, ОУ) – устройство, требуемый режим работы которого должен поддерживаться извне специально организованными управляющими воздействиями.
Управление – формирование управляющих воздействий, обеспечивающих требуемый режим работы ОУ.
Регулирование – частный вид управления, когда задачей является обеспечение постоянства какой-либо выходной величины ОУ.
Автоматическое управление – управление, осуществляемое без непосредственного участия человека.
Входное воздействие (Х) – воздействие, подаваемое на вход системы или устройства.
Выходное воздействие ( Y ) – воздействие, выдаваемое на выходе системы или устройства.
Внешнее воздействие – воздействие внешней среды на систему.
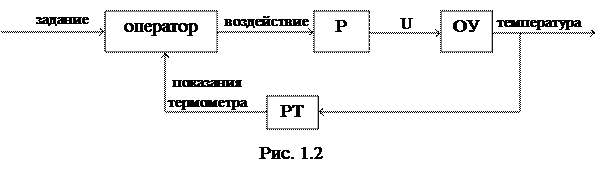
Структурная схема системы регулирования к примеру 1 изображена на рис. 1.2.
 |
Пример 2. Схема автоматического регулирования температуры сушильного шкафа.
В схеме используется ртутный термометр с контактами РТК. При повышении температуры до заданной контакты замыкаются столбиком ртути, катушка релейного элемента РЭ возбуждается и цепь нагревателя Н размыкается контактом РЭ. При понижении температуры контакты термометра размыкаются, реле обесточивается, возобновляя подачу энергии на объект (см. рис. 1.3). ¨
 |
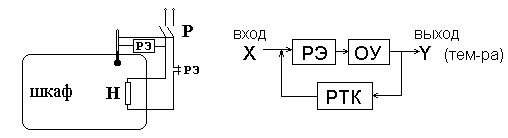Рис. 1.3
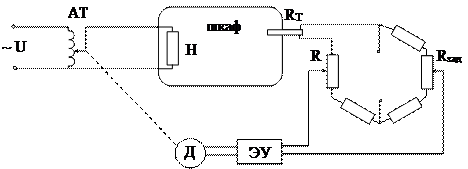
Пример 3. Схема АСР температуры с измерительным мостом.
При температуре объекта, равной заданной, измерительный мост М (см. рис. 1.4) уравновешен, на вход электронного усилителя ЭУ сигнал не поступает и система находится в равновесии. При отклонении температуры изменяется сопротивление терморезистора RТ и равновесие моста нарушается. На входе ЭУ появляется напряжение, фаза которого зависит от знака отклонения температуры от заданной. Напряжение, усиленное в ЭУ, поступает на двигатель Д, который перемещает движок автотрансформатора АТ в соответствующую сторону. При достижении температуры, равной заданной, мост сбалансируется и двигатель отключится.
 | |||
 | |||
Рис. 1.4
Величина заданного значения температуры устанавливается с помощью резистора Rзад. ¨
Исходя из описанных примеров, можно определить типовую структурную схему одноконтурной АСР (см. рис. 1.5). Принятые обозначения:
x - задающее воздействие (задание), e = х - у - ошибка регулирования, u - управляющее воздействие, f - возмущающее воздействие (возмущение).
 |
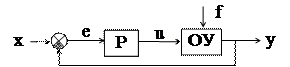Рис. 1.5
Определения:
Задающее воздействие (то же, что входное воздействие Х) - воздействие на систему, определяющее требуемый закон изменения регулируемой величины).
Управляющее воздействие (u) - воздействие управляющего устройства на объект управления.
Управляющее устройство (УУ) - устройство, осуществляющее воздействие на объект управления с целью обеспечения требуемого режима работы.
Возмущающее воздействие (f) - воздействие, стремящееся нарушить требуемую функциональную связь между задающим воздействием и регулируемой величиной.
Ошибка управления (е = х - у) - разность между предписанным (х) и действительным (у) значениями регулируемой величины.
Регулятор (Р) - комплекс устройств, присоединяемых к регулируемому объекту и обеспечивающих автоматическое поддержание заданного значения его регулируемой величины или автоматическое изменение ее по определенному закону.
Автоматическая система регулирования (АСР) - автоматическая система с замкнутой цепью воздействия, в котором управление (u) вырабатывается в результате сравнения истинного значения у с заданным значением х.
Дополнительная связь в структурной схеме АСР, направленная от выхода к входу рассматриваемого участка цепи воздействий, называется обратной связью (ОС). Обратная связь может быть отрицательной или положительной.
1.2. Классификация АСР.
1. По назначению (по характеру изменения задания):
· стабилизирующая АСР - система, алгоритм функционирования которой содержит предписание поддерживать регулируемую величину на постоянном значении (x = const);
· программная АСР - система, алгоритм функционирования которой содержит предписание изменять регулируемую величину в соответствии с заранее заданной функцией (x изменяется программно);
· следящая АСР - система, алгоритм функционирования которой содержит предписание изменять регулируемую величину в зависимости от заранее неизвестной величины на входе АСР (x = var).
2. По количеству контуров:
· одноконтурные - содержащие один контур,
· многоконтурные - содержащие несколько контуров.
3. По числу регулируемых величин:
· одномерные - системы с 1 регулируемой величиной,
· многомерные - системы с несколькими регулируемыми величинами.
Многомерные АСР в свою очередь подразделяются на системы:
а) несвязанного регулирования, в которых регуляторы непосредственно не связаны и могут взаимодействовать только через общий для них объект управления;
б) связанного регулирования, в которых регуляторы различных параметров одного и того же технологического процесса связаны между собой вне объекта регулирования.
4. По функциональному назначению:
АСР температуры, давления, расхода, уровня, напряжения и т.д.
5. По характеру используемых для управления сигналов:
· непрерывные,
· дискретные (релейные, импульсные, цифровые).
6. По характеру математических соотношений:
· линейные, для которых справедлив принцип суперпозиции;
· нелинейные.
Принцип суперпозиции (наложения): Если на вход объекта подается несколько входных воздействий, то реакция объекта на сумму входных воздействий равна сумме реакций объекта на каждое воздействие в отдельности:
 |
L(х1 + х2) = L(х1) + L(х2),
где L - линейная функция (интегрирование, дифференцирование и т.д.).
7. По виду используемой для регулирования энергии:
· пневматические,
· гидравлические,
· электрические,
· механические и др.
8. По принципу регулирования:
· по отклонению:
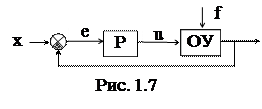Подавляющее большинство систем построено по принципу обратной связи - регулирования по отклонению (см. рис. 1.7).
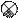Элемент называется сумматором. Его выходной сигнал равен сумме входных сигналов. Зачерненный сектор говорит о том, что данный входной сигнал надо брать с противоположным знаком.
· по возмущению.
Данные системы могут быть использованы в том случае, если есть возможность измерения возмущающего воздействия (см. рис. 1.8). На схеме обозначен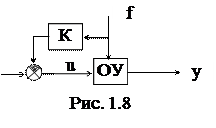 
К - усилитель с коэффициентом усиления К.
· комбинированные - сочетают в себе особенности предыдущих АСР.
Данный способ (см. рис. 1.9) достигает высокого качества управления, однако его применение ограничено тем, что возмущающее воздействие f не всегда можно измерить.
 |
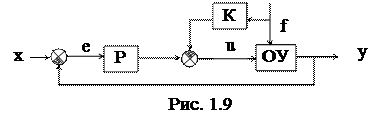1.3. Классификация элементов автоматических систем.
1. По функциональному назначению:
· измерительные,
· усилительно-преобразовательные,
· исполнительные,
· корректирующие.
2. По виду энергии, используемой для работы:
· электрические,
· гидравлические,
· пневматические,
· механические,
· комбинированные.
3. По наличию или отсутствию вспомогательного источника энергии:
· активные (с источником энергии),
· пассивные (без источника).
Дата: 2019-04-23, просмотров: 215.
