По таблице 11.12 (4, с. 370) для заданной передаваемой мощности подходят ремни сечений О, А и Б. Чтобы найти оптимальное решение, рассчитываем все три варианта (4, с. 375). Результаты расчета сводим в таблицу 1.
Таблица 1. Расчета клиноременной передачи (Рэд = 0,4 кВт, n эд = 100 об/мин, i = 2)
| Определяемые величины | Расчетные формулы | Сечение ремня | |
| О | А | ||
| 1 | 2 | 3 | 4 |
| Ширина ремня b 0, мм Толщина ремня h, мм Площадь поперечного сечения F , мм2 Диаметр малого шкива D 1, мм Диаметр большого шкива D 2, мм Ближайший диаметр по стандарту Расчетное передаточное число при ξ= 0,01 Скорость ремня, м/с | По табл. 11.11 (4, с.370)
По табл. 11.11 (4, с.370)
По табл. 11.11 (4, с.370)
По табл. 11.13 (4, с.371)
D 2 ≈ D 1 ∙ i ∙(1- ξ)
По табл. 11.13 (4, с.371)
i = 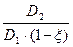 V =
V = 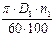
| 10 6 47 80 158 160 2,0 4,19 | 13 8 81 125 248 250 2,0 6,54 |
| Продолжение таблицы 1 | |||
| 1 | 2 | 3 | 4 |
| Межосевое расстояние, мм Расчетная длина ремня L р, мм Ближайшая стандартная длина ремня L, мм Межосевое расстояние А, мм Угол обхвата малого шкива a, град. Число пробегов Коэффициенты Окружное усилие Р, Н Число ремней Напряжения, при σ0 = 1,2 Н/мм2, ρ = 1,2 Еи = 80 Н/мм2 Полное напряжение, Н/мм2 Расчетная долговечность, ч. при m=8, σv=9 Н/мм2, Сi=1,8 и Сн=1 Сила давления на валы, Н | A ≈ D 2
L=2∙A+ 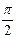 ∙(D 1+D 2)+ ∙(D 1+D 2)+ 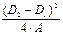 По табл. 11.11 (4, с.370)
A=
По табл. 11.11 (4, с.370)
A= 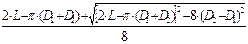 α=180-60∙
α=180-60∙ 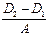 ν =
ν = 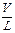 Сα = 1-0,003(180-α)
С v = 1,05-0,0005∙V2
Ср - по табл. 11.7 (4, с.359)
k 0 - по табл. 11.14 (4, с.373)
Р =
Сα = 1-0,003(180-α)
С v = 1,05-0,0005∙V2
Ср - по табл. 11.7 (4, с.359)
k 0 - по табл. 11.14 (4, с.373)
Р = 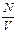 = = 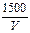 z =
z = 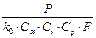 σ1 = σ0 +
σ1 = σ0 + 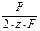 σ v = ρ∙V2∙10-6
σ и = Еи∙
σ v = ρ∙V2∙10-6
σ и = Еи∙ 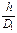 σ max = σ1 + σ v + σи
h =
σ max = σ1 + σ v + σи
h = 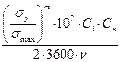 Q = 2∙ σ0 ∙z∙F∙sin
Q = 2∙ σ0 ∙z∙F∙sin 
| 160 697 710 162 150 5,90 0,91 1,04 1 1,57 95,5 2,00 2,22 0,02 6,00 8,24 861 55,77 | 250 1089 1120 258 151 5,84 0,91 1,03 1 1,7 61,1 1,00 1,58 0,05 5,12 6,75 4280 94,45 |
Выбираем сечение ремня О, тогда сила давления на валы F в = 55,77 Н.
Расчет вала на изгиб
Рассчитаем вал на изгиб (рисунок 1).
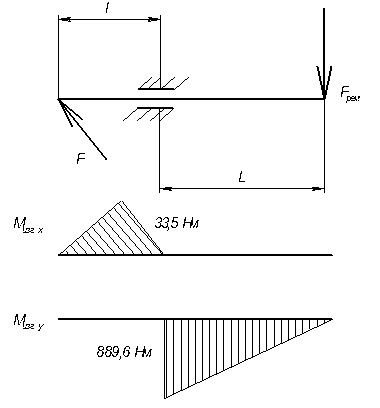
Рисунок 1 – К расчету вала на изгиб.
Изгибающее напряжение
σизг = 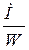 . (8)
. (8)
В вертикальной плоскости момент будет
Мизг у = Fрем ∙ L ∙ n, (10)
где L − расстояние от места приложения ремней до опоры, L = 0,15 м;
n − количество ремней;
Fрем − сила от натяжения одного ремня:
Fрем = 2 ∙ Q = 2 ∙ 55,77 = 111,54 Н;
Мизг у = 111,54 ∙ 0,15 ∙ 2 = 33,5 Н∙м.
В горизонтальной плоскости момент будет
Мизг х = F ∙ l = 12,7 ∙ 103 ∙ 0,07 = 889 Н∙м.
В опасном сечении момент будет
Мизг = 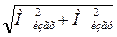 =
= 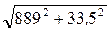 = 889,6 Н∙м.
= 889,6 Н∙м.
Вал в опасном сечении представляет круг диаметром 0,035 м. Определим момент его сопротивления изгибу.
Момент сопротивления сечения относительно нейтральной оси (для круглого сечения) рассчитывается по формуле:
Wz = π ∙ d3 / 32 = 0,1 ∙ d3; (11)
где d − диаметр сечения.
Wz = 0,1 ∙ 0,0353 = 4,3 ∙ 10−6 м3.
Определим напряжение, возникающее от изгиба
σизг = Mизг / W = 889,6 / (4,3 ∙ 10–6) = 206,8 МПа.
Условие прочности: [σизг] ≥ σизг.
Для материала вала − стали 45 − допускаемое напряжение на изгиб [σизг] = 280 МПа.
Условие прочности выполняется, т. к. допускаемое напряжение на изгиб больше действительного.
Расчет шпильки на растяжение
Шпилька испытывает нагрузку сжатия от сил натяжения ремней (рисунок 2)
Для стали Ст 45 допускаемое напряжение на растяжение [σрас] = 160 МПа.
σсж = Q / S, (12)
где Q − действующая нагрузка в одной шпильке;
Q = F / 4 = 111,54 / 4 = 27,9 Н;
S − площадь поперечного сечения шпильки.
Рисунок 2 − Схема и эпюра сжатия шпильки.
Площадь поперечного сечения шпильки
S = p ∙ dшп2 / 4, (13)
где dшп − требуемый диаметр шпильки.
Принимаем диаметр шпильки dшп = 0,006 м, тогда
S = 3,14 ∙ 0,0062 / 4 = 2,82 ∙ 10−6 м2.
Должно выполняться условие
[σрас] ≥ σрас = Q / F. (14)
σрас = Q / F = 27,9 / 2,82 ∙ 10−6 = 9,89 МПа.
Так как [σрас] = 160 МПа, то условие выполняется.
Дата: 2019-04-23, просмотров: 245.