Выбор оптимального варианта трассы сводится к выявлению такого положения головной магистрали, при котором суммарная металлоемкость ответвлений к потребителям имеет минимальное значение.

В этом случае используется метод математической статистики, который позволяет найти уравнение прямой (кривой) линии, расположенной на минимальном расстоянии от нескольких случайных точек (метод наименьших квадратов).

Суть метода заключается в следующем. На генеральном плане населенного пункта, промплощадки или какой-либо другой территории произвольно наносится система координат XOY и на ней фиксируется положение потребителей (рис. 2).

Поскольку общая металлоемкость ответвлений прямо пропорциональна их суммарной длине и среднему диаметру, при выборе оптимального варианта трассировки головной магистрали необходимо учитывать не только количество и положение потребителей, но и их нагрузка.

Анализ гидравлических режимов эксплуатации систем газо- и теплоснабжения показывает, что диаметр трубопровода при прочих равных условиях определяется расходом транспортируемой среды G в степени m. Показатель степени имеет следующие численные значения:

газопроводы низкого давления m = 0,368;

трубопроводы тепловых сетей m = 0,38;

газопроводы высокого (среднего) давления m = 0,38.

Для определения расчетных координат головной магистрали распределительного трубопровода используется следующее выражение (6.1):

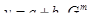  (6.1)

где x, y – расчетные координаты магистрали;

a, b – искомые параметры прямой.

Задача заключается в нахождении наименьшей суммы квадратов отклонений расчетных значений координат по уравнению

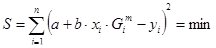 (6.2)

где n – количество ответвлений к потребителям;

x_i, y_i – заданные координаты потребителей.

Дифференцируя функцию S по искомым параметрам a и b и приравнивая полученные выражения к нулю, приходим к следующей системе:

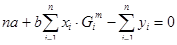(6.3)

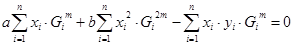
решая которую, находим a_opt, b_opt и оптимальную трассировку трубопровода:

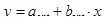 (6.4)

В частном случае, когда нагрузки потребителей одинаковы, то есть

G_i = const, целевая функция задачи (6.2) трансформируется в уравнение

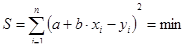  (6.5)

Нахождение искомых значений параметров a_opt, b_opt сводится к решению следующей системы:

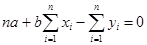 (6.6)

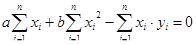
Пример: Найти оптимальную трассировку распределительного трубопровода на три потребителя с координатами

x₁ = 1,0 км; y₁ = 1,5 км;

x₂ = 3,0 км; y₂ = 2,5 км;

x₃ = 5,0 км; y₃ = 3,0 км;

x₄ = 8,0 км; y₄ = 9,0 км.

Нагрузки потребителей одинаковы.

Подставляя координаты в уравнение (6.6), получим

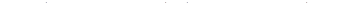
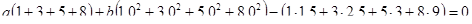
После преобразований имеем

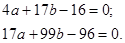
откуда a_opt = -0,45; b_opt = 1,05.

Таким образом, оптимальное положение головной магистрали распределительного трубопровода определяется уравнением:

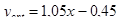 (6.7)

В общем случае, когда конфигурация головной магистрали представляет собой ломаную линию, содержащую k линейных участков, задача решается последовательно для каждого участка трубопровода. При этом условие оптимальной трассировки магистрали реализуется следующей системой уравнений:

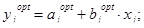 где j = 1,2,….k. (6.8)

Если при реальном проектировании осуществить оптимальную трассировку не представляется возможным (специфика рельефа местности, особенности застройки населенного пункта и другие обстоятельства), принимаем тот вариант трассы, который обеспечивает максимальное приближение к оптимальному с учетом заданных ограничений.