4Как определяется коэффициент усиления транзисторного усилителя при схеме с общим эмиттером?
5Объясните назначение элементов схемы, работу и применение генераторов синусоидального напряжения типа LC и RC.
6Объясните структурный состав, основные функции микропроцессора и укажите существенное отличие микропроцессора от микро-ЭВМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Указания к решению задачи 1
Решение задачи 1 требует знания материала темы «Электрические цепи постоянного тока»: основных законов цепей постоянного тока (законов Ома, Кирхгофа, последовательного и параллельного соединения резисторов), производных формул этих законов и умения их применять для расчета электрических цепей со смешанным соединением резисторов.
Расчет электрических цепей со смешанным соединением резисторов выполняется путем постепенного упрощения схемы в следующей последовательности:
1Определить узлы и ветви схемы; обозначить стрелками направление токов во всех ветвях
23аменить группу последовательно соединенных резисторов эквивалентным сопротивлением участка цепи
3Заменить группу параллельно соединенных резисторов также их эквивалентным сопротивлением
4Найти эквивалентное сопротивление всей цепи
5Определить силу тока в неразветвленной части цепи
6Посредством обратного преобразования найти разность потенциалов (напряжение) на отдельных резисторах и силу тока во всех ветвях
7Проверить правильность выполненных расчетов.
Методику и последовательность действий при решении задач со смешанным соединением резисторов рассмотрим в общем виде на конкретном примере.
Условие задачи. Цепь постоянного тока со смешанным соединением состоит из четырех резисторов. Заданы схема цепи (рисунок 1), значения сопротивлений резисторов: R1 = 30 Ом, R2 = 20 Ом, R3 = 3 Ом, R4 = 5 Ом, мощность цепи Р = 320 Вт.
Определить: эквивалентное сопротивление цепи Rэк; 2) токи, проходящие через каждый резистор I1 – I4 . Решение задачи проверить, применив законы Кирхгофа. Составить баланс мощностей.
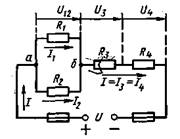
Рисунок 1
Выписываем условие задачи (содержание условий задач выписывать применительно к своему варианту) и продумываем план (порядок) решения.
В нашем случае принимаем такой порядок решения:
1. Определяем, что в данной схеме (рисунок 1) два узла (а, б) и три ветви, в каждой из которых протекает свой ток: I1, I2, I = I3 = I4
2. Находим эквивалентное сопротивление цепи, заменяя группу параллельно соединенных резисторов R1 и R2 их эквивалентным сопротивлением R1,2
R1,2 = R1R2 / (R1+R2)
Схема примет вид (рисунок 2):
R1,2 R3 R4
 |











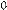
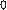


+ - Рисунок 2
где R1,2; R3; R4 соединены последовательно и их общее (эквивалентное) сопротивление определяется по формуле:
Rэк = R1,2 + R3 + R4
3. Из формулы мощности находим общий ток в неразветвленной части цепи ( I ) и токи во всех ветвях ( I1, I2, I3, I4 ):
P=I2Rэк → I= 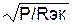 ;
;
I3 = I4 = I, так как при последовательном соединении на всех участках цепи один и тот же ток.
Токи I1, I2 - определяются по закону Ома для участка цепи
I1 = U1,2 / R1; I2 = U1,2 / R2,
где U1,2 = I R1,2 - падение напряжения на параллельном участке цепи:
U1,2 = Uаб =U1 = U2
4. Выполняем решение, не забывая нумеровать и кратко описывать действия. Отсутствие письменных пояснений действий приводит к неполному пониманию решения задач, быстро забываются.
5. Выполняем проверку решения следующими способами: а) логичность получения такого результата; б) проверка результатов с применением первого и второго закона Кирхгофа, подсчетом баланса мощности; в) сравнивание результатов решением задачи другими способами
Объясним некоторые способы проверки результатов решения.
Применение первого закона Кирхгофа.
Формулировка закона: алгебраическая сумма токов в любой узловой точке электрической цепи равна нулю.
Математическая запись для узла б схемы цепи рисунок 1:
I1+I2 = I или I1+I2 - I = 0.
Применение второго закона Кирхгофа.
Формулировка закона: во всяком замкнутом контуре электрической цепи алгебраическая сумма ЭДС ( ∑Е ) равна алгебраической сумме падений напряжений ( ∑ IR ) на отдельных сопротивлениях этого контура.
В замкнутом контуре (рисунок 1) приложенное напряжение U аналогично ЭДС при внутреннем сопротивлении источника тока, равном нулю. Падения напряжения на сопротивлениях контура равны:
U1,2 = I R1,2; U3=I R3 и U4 = I R4.
Обходя контур по направлению тока ( в данном случае по часовой стрелке), составим уравнение по второму закону Кирхгофа:
U = U1,2+U3+U4.
Подсчет баланса мощности.
Общая мощность цепи равна сумме мощностей на отдельных резисторах.
Для схемы цепи (рисунок 1) Р=Р1+Р2+Р3+Р4; так как Р = U I = I2 R, то
Р = I12 ∙ R1+ I22R2+ I32R3+ I42R4
Для закрепления материала рекомендуется рассмотреть решение примеров 1 - 3.
Пример 1. На рисунке 3 изображена электрическая цепь со смешанным соединением резисторов. Известны значения сопротивлений резисторов R1 = 3 Ом, R2 = 10 Ом, R3 = 15 Ом, R4 = 1 Ом, напряжение U= 110 B и время работы цепи t = 10 ч. Определить токи, проходящие через каждый резистор, I1, I2, I3, I4, общую мощность цепи Р и расход энергии W.
Дано : R1 = 3 Ом, R2 = 10 Ом, R3 = 15 Ом, R4 = 1 Ом, U= 110 B, t = 10 ч. Определить : I1, I2, I3, I4
Решение
1. В схеме два узла и три ветви. Обозначим стрелками токи, проходящие через каждый резистор, с учетом их направления (рисунок 3).
2. Определим общее эквивалентное сопротивление цепи, метод подсчета которого для цепи со смешанным соединением резисторов сводится к последовательному упрощению схемы.
Сопротивления R2 и R3 соединены параллельно. Найдем общее сопротивление при таком соединении:
1/R2,3 =1/R2+1/R3,
или, приводя к общему знаменателю, получим
R2,3 = R2R3 / (R2+R3) = 10 ∙15 / (10+15) = 150 / 25 = 6 Ом.
Схема примет вид: (рисунок 4), где резисторы R2,3, R1, R4 соединены последовательно, их общее (эквивалентное) сопротивление равно:
Rэк = R1+R2,3+R4 = 3+6+1 = 10 Ом.
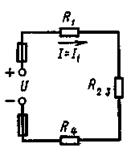
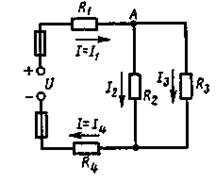
Рисунок 3 Рисунок 4
3. По закону Ома для внешнего участка цепи определим общий ток
I = U / Rэк=110 / 10 =11А.
4.Найдем токи, проходящие через все резисторы. Через резистор R1 проходит ток I1 = I. Через резистор R4 проходит ток I4 = I.
Для определения токов, проходящих через резисторы R2 и R3, нужно найти напряжение на параллельном участке U2,3. Это напряжение можно определить двумя способами:
U2,3 = I R2,3 = 11 ∙ 6 = 66 В
или U2,3 = U - I R1 - I R4 = U - I(R1+R4) = 110 - 11(3+1) = 66 В.
По закону Ома для параллельного участка цепи найдем
I2 = U2,3 / R2 = 66/10 = 6,6 A; I3 = U2,3 / R3 = 66/15 = 4,4 A или,
5. Найдем общую мощность цепи:
Р = UI = 110 ∙ 11 = 1210 Вт = 1,21 кВт
6. Определим расход энергии:
W = Р t = 1,21 ∙ 10 = 12,1 кВт ∙ ч
7. Выполним проверку решения задачи описанными ранее способами:
а) проверим баланс мощности
P = P1 +P2+ P3 + P4 = I12 R1 + I22 R2+I32 R3+I42 R4 = 112∙3 + 6,6 2 ∙ 10+ 4,42∙15 + 112 ∙ 1 = 363 + 435,6 + 290,4 + 121 = 1210 Вт = 1,21кВт;
1210 Вт = 1210 Вт;
б) для узловой точки А схемы рисунка 2 применим первый закон Кирхгофа:
I = I2 + I3 = 6,6 + 4,4 A = 11А;
11A = 11A;
в) составим уравнение по второму закону Кирхгофа, обходя контур цепи по часовой стрелке,
U = U1 + U2,3 + U4 = IR1 + IR2,3 + IR4
110 = 11 ∙ 3 + 11 ∙6 + 11 ∙ 1
110 В = 110 В
Все способы проверки подтверждают правильность решения задачи. В вашем варианте достаточно использовать только тот способ, который предусмотрен условием.
Пример 2. Электрическая цепь, состоящая из нескольких резисторов, имеет эквивалентное сопротивление Rэк1 = 10 Ом. Каким способом, и какой, по величине сопротивления, резистор Rx следует подключить к цепи, чтобы увеличить эквивалентное сопротивление этой цепи до величины Rэк2 = 25 Ом?
Дано: Rэк1 = 10 Ом, Rэк2 = 25 Ом.
Определить значение и способ подключения Rx.
Решение:
При последовательном соединении резисторов эквивалентное сопротивление цепи равно сумме их сопротивлений. Так как эквивалентное сопротивление цепи Rэк2 по сравнению с прежним значением Rэк1 увеличивается, то резистор Rx надо включить в цепь последовательно:
Rэк2 = Rэк1 + Rx → Rx = Rэк2 - Rэк1= 25 - 10 = 15 Ом.
Ответ: Rx = 15 Ом (Рисунок 5)
Пример 3. Электрическая цепь, состоящая из нескольких резисторов, имеет эквивалентное сопротивление Rэк1 = 10 Ом. Каким способом, и какой, по величине сопротивления, резистор Rx следует подключить, чтобы уменьшить эквивалентное сопротивление цепи до Rэк2 = 6 Ом?
Дано: Rэк1 = 10 Ом, Rэк2 = 6 Ом.
Определить значение и способ подключения Rx.
Решение:
При параллельном соединении резисторов обратное значение эквивалентного сопротивления цепи равно сумме обратных значений сопротивлений отдельных резисторов
1/ Rэк = 1/R1 + 1/R2 + …+1/Rn
и будет меньше наименьшего сопротивления резисторов. Например, параллельно соединены резисторы сопротивлениями 100, 50, 10; 0,5 Ом. Эквивалентное сопротивление такого соединения меньше 0,5 Ом.
По условию задачи, эквивалентное сопротивление Rэк2 меньше первоначального значения Rэк1, поэтому резистор Rx подключается к цепи параллельно, а значение его сопротивления определяют следующим образом:
1/Rэк1 + 1/Rx → 1/Rx = 1/Rэк2 - 1/ Rэк1 = 1/6 - 1/10 = 1/15.
Ответ: Rx = 15 Ом (рисунок 6)
Применяя описанную методику, рекомендуется решить задачи 1 - 3, к которым даны ответы для контроля правильности решения.
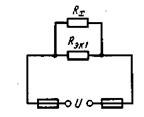
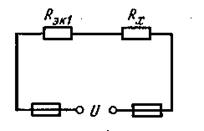
Рисунок 5 Рисунок 6
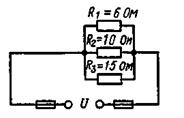
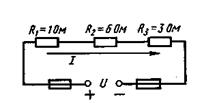
Рисунок 7 Рисунок 8
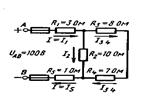
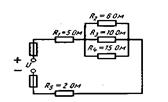
Рисунок 9 Рисунок 10
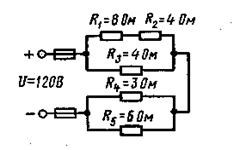
Рисунок 11
Задача1.Определить эквивалентное сопротивление схем электрических цепей, приведенных на рисунке 7 - 11.
Ответ: Rэк = 10 Ом (рисунок 7), Rэк = 3 Ом (рисунок 8),
Rэк = 10 Ом (рисунок 9).
Задача 2 Определить эквивалентное сопротивление цепи (рисунок 10), токи, проходящие через каждое сопротивление, стоимость электрической энергии за время t = 10ч, если 1 кВт∙ч стоит по действующему тарифу.
Ответ: Rэк =10 Ом, I = I1 = I5 = 10 A, I2= 6 A, I3,4 = 4 A, стоимость электрической энергии по действующему тарифу.
Задача 3 Для схемы, изображенной на рисунке 11, определить эквивалентное сопротивление, напряжения на каждом сопротивлении.
Ответ: Rэк = 5 Ом, U3 = 72 B, U1 = 48 B, U2 = 24 B,
U45 = U4 + U =48B.
Указания к решению задачи 2
Для решения задачи 2 нужно знать программный материал темы "Трехфазные цепи переменного тока", отчетливо представлять соотношения между фазными и линейными значениями токов и напряжений при соединении потребителей электрической энергии звездой и треугольником.
Для ознакомления с общей методикой решения задач данной темы приведены формулы, показано их практическое применение.
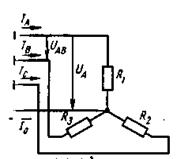
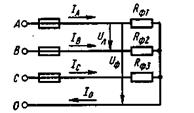
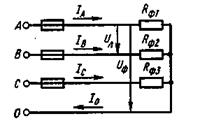
Соединение потребителей звездой. На рисунке 12 (а – в) показано разное выполнение схем такого соединения с нейтральным проводом и без него.
 | |||
 | |||
 | |||
 | |||
а) б) в)
Рисунок 12
Принятые обозначения на схемах:
линейное напряжение U л = UAB = UBC = UCA;
фазные напряжения U ф, UA, UВ, UС;
линейные токи (они же фазные токи) I л , I ф, IA, IB, IC,
ток в нейтральном (нулевом) проводе, равен геометрической сумме фазных токов
I О = I А + I В + I С
При равномерной нагрузке фаз ток I 0 = 0 и надобность в нем отпадает
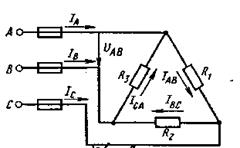
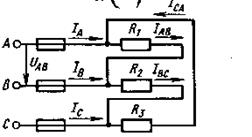
Соединение потребителей треугольником. На рисунке 13 (а, б) показано разное выполнение схем такого соединения.
Принятые обозначения на схемах:
линейные (они же фазные) напряжения: U л = U ф = UAB = UBC = UCA,
фазные токи: I ф, IAB, IBC, ICA,
линейные токи: I л; IA; IB; IC.
а) б)
Рисунок 13
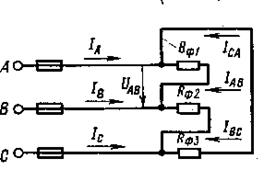
Рисунок 14
Подсчет активной мощности для любого соединения в трехфазных цепях выполняется по формулам:
фазные мощности: РфА = UфА IфА cos φфА
РфВ = UфВ IфВ cos φфВ
РфС = UфС IфС cosфС
общая мощность: Р = РфА+ РфВ + РфС
При равномерной нагрузке фаз общая мощность трехфазной цепи:
Р = 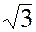 Uл Iл cos φф.
Uл Iл cos φф.
или Р = 3 Рф
Для подсчета параметров ламп накаливания (Рламп) и электронагревательных элементов ТЭНов (Рнагр) нужно применять формулы:
Рламп = UлампIламп cos φламп,
Pнагр = Uнагр Iнагр ∙ cos φнагр;
учитывая, что cos φламп= cos φнагр = 1, так как эта нагрузка активная.
Применение формул рассмотрим в решенных примерах.
Пример 4. Три активных сопротивления Rф1 = 22 Ом, Rф2= 27,5 Ом, Rф3 = 11 Ом соединены треугольником и присоединены к трехпроводной трехфазной линии с линейным напряжением Uл = 220 В (рисунок 14). Определить фазные (IAB, IBC,ICA) и линейные (IA,IB,IC) токи, фазные мощности (Рф1,Рф2, Рф3) и общую (Р) мощность трехфазной цепи.
Дано: Uл = 220 В; Rф1 = 22 Ом, Rф2= 27,5 Ом, Rф3 = 11 Ом
Определить: IAB, IBC, ICA, IA, IB, IC, Рф1, Рф2, Рф3, Р
Решение
Найдем значение фазных токов по закону Ома:
Iф1 = Uф1/ Zф1; Iф2 = Uф2/ Zф2; Iф3 = Uф3/ Zф3.
Так как в каждой фазе приемника энергии только по одному активному сопротивлению, то полные сопротивления фаз будут равны:
Zф1 = Rф1; Zф2 = Rф2; Zф3 = Rф3.
Зная, что при соединении треугольником линейное напряжение равно фазному: Uл = Uф1 = Uф2 = Uф3 = 220В
окончательно получим:
Iф1 = Uф / Rф1 = 220/22 = 10 А;
Iф2 = Uф / Rф2 = 220/27,5 = 8 А;
Iф3 = Uф / Rф3 = 220/11 = 20 А.
В этом случае линейные токи IA, IB, IC нужно определить по векторной диаграмме, которую необходимо строить в масштабе по данным задачи и вычисленным значениям фазных токов. Подробное построение векторной диаграммы описано далее.
Обратите особое внимание на порядок построения и точность вычерчивания диаграммы, так как от этого зависит, насколько правильно будут определены величины линейных токов.
1. Выписываем значения токов и напряжения:
напряжения: Uл = UAB = UBC = UCA = 220 B;
фазные токи: Iф1= IAB=10 A; Iф2 = IBC = 8 A; Iф3 = ICA = 20 A.
2. Задаемся масштабом: по току m1 = 8 A/см по напряжению mU = 66 В/см.
3. Определяем длину векторов напряжений и токов
L 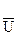 AB = L
AB = L 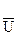 BC = L
BC = L 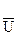 CA = Uл / mU = 220 B / 66 B/см = 3,33 см;
CA = Uл / mU = 220 B / 66 B/см = 3,33 см;
LIAB = IAB / m1 = 10 A / 8 A/см = 1,25 см;
LIBC = 1 см и LICA = 2,5 см.
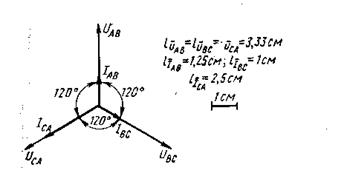
Рисунок 15
4. Откладываем векторы фазных (линейных) напряжений найденной длины под углом 120 ° относительно друг друга (рисунок 15).
5. В фазах с 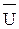 AB,
AB, 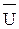 BC,
BC, 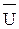 CA откладываем векторы фазных токов IAB, IBC, ICA, вдоль векторов напряжений, так как по условию задачи нагрузка всех приемников энергии активная, т.е. углы сдвига фаз равны нулю
CA откладываем векторы фазных токов IAB, IBC, ICA, вдоль векторов напряжений, так как по условию задачи нагрузка всех приемников энергии активная, т.е. углы сдвига фаз равны нулю
(φ = φф1 = φф2 = φф3 = 0).
6. Векторы линейных токов  A,
A,  B,
B,  C определяем из соответствующей геометрической разности фазных токов (Рисунок 16):
C определяем из соответствующей геометрической разности фазных токов (Рисунок 16):
 A =
A =  AB -
AB -  CA;
CA;  B =
B =  BC -
BC -  AB;
AB;  C =
C = 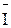 CA -
CA - 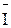 BC
BC
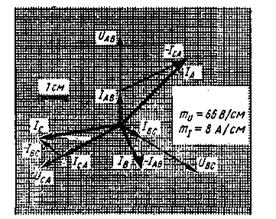
Рисунок 16
Вычитание векторов можно свести к геометрическому сложению. Для этого к векторам  АВ,
АВ,  ВС,
ВС,  СА следует прибавить векторы
СА следует прибавить векторы  СА,
СА,  АВ,
АВ, 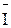 ВС, предварительно повернув их на 180 °; получим на векторной диаграмме векторы -
ВС, предварительно повернув их на 180 °; получим на векторной диаграмме векторы - 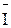 СА, -
СА, - 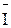 АВ, -
АВ, - 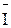 ВС.
ВС.
Сложение векторов, например,  АВ и -
АВ и -  СА и т.д. следует выполнять по правилу многоугольника, когда к концу одного вектора пристраивают начало другого, а замыкающий вектор является результирующим, т.е. в данном случае линейный ток
СА и т.д. следует выполнять по правилу многоугольника, когда к концу одного вектора пристраивают начало другого, а замыкающий вектор является результирующим, т.е. в данном случае линейный ток
 А =
А =  АВ -
АВ -  СА =
СА =  АВ + (-
АВ + (-  СА).
СА).
Аналогично, для токов  В,
В,  С.
С.
Измерив линейкой длину векторов линейных токов и зная масштаб для тока mI, определяем их числовые значения. Например, LIA = 3,4 см. Тогда IA =LIAmI = 3,4 см ·8 А/см = 27,2 А. Аналогично IB= 16 A и IC = 24 A.
Зная вычисленные значения фазных токов Iф1, Iф2, Iф3 и сопротивления приемников энергии Rф1, Rф2, Rф3, можно определить фазные Рф1, Рф2, Рф3 и общую Р мощности трехфазного потребителя энергии.
а) Фазные мощности Так как нагрузка активная, то и мощности приемников энергии активные. Активная мощность первой фазы
Рф1 = Uф1Iф1cos φф1.
Учитывая, что при активной нагрузке φф = 0, а cos φф = 1, получим
Рф1 = UфIф1, но Uф1 = Iф1Rф1,
тогда Рф1 = I2ф1Rф1.
Для второй и третьей фаз: Рф2 = I2ф2Rф2; Рф3 = I2ф3Rф3.
Подставляя значения токов и сопротивлений получим:
Рф1 = РАВ = I2ф1Rф1 = 102·22 = 100·22 = 2200 Вт = 2,2 кВт;
Рф2 = РВС = I2ф2Rф2 = 82·27,5 =64·27,5= 1760 Вт = 1,76 кВт;
Рф3 = РСА = I2ф3Rф3 = 202·11 = 400·11 = 4400 Вт = 4,4 кВт.
б) Активная мощность трехфазной цепи.
Для ее подсчета нельзя применить формулу
Р = 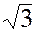 Uл Iл cosφф
Uл Iл cosφф
так как в данном примере нагрузка приемников энергии неравномерная.
Поэтому активную мощность трехфазной цепи можно определить как сумму фазных мощностей всех трех приемников энергии:
Р = Рф1+ Рф2 + Рф3 = 2,2 + 1,76 + 4,4 = 8,36 кВт.
Пример 5. Три одинаковых потребителя, имеющих активные сопротивления Rф1 = Rф2 = Rф3 = 10 Ом, соединены треугольником (рисунок 14) и подключены к трехфазной электрической цепи с линейным напряжением Uл = 220 В. Определить: фазные IAB, IBC, ICA и линейные IA, IB, IC токи, фазные мощности РАВ, РВС, РСА и общую активную мощность трехфазной цепи Р.
Дано: Rф1 = Rф2 = Rф3 = 10 Ом, Uл = 220 В.
Определить: IAB, IBC, ICA, IA, IB, IC, РАВ, РВС, РСА
Решение
1. Фазные токи IAB, IBC, ICA определим по закону Ома для фазы
Iф = Uф / Zф.
По условию задачи все фазы нагружены одинаково сопротивлениями R = 10 Ом. При соединении треугольником линейные напряжения равны фазным, значит, в данном случае Uф = 220 В. Тогда
Iф = IAB = IBC = ICA = Uф / R = 220/10 = 22 A
2. Линейные токи найдены по формуле, определяющей соотношение между линейными и фазными токами при одинаковой нагрузке фаз, что соответствует условиям задачи:
IA = IB = IC= 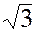 Iф = 1,73 · 22 = 38 А.
Iф = 1,73 · 22 = 38 А.
3. Фазные мощности определим по формуле
Рф = РАВ = РВС = РСА = I2 Rф = 222 · 10 = 4840 Вт.
Тогда мощность трехфазной цепи
Р = 3Рф= 3 · 4840 = 14520 Вт = 14,5 кВт.
Так как нагрузка фаз одинаковая, мощность цепи также можно найти по формуле
Р = 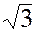 UлIлcosφф = 1,73 · 220 · 38 · 1 = 14480 Вт = 14,5 кВт.
UлIлcosφф = 1,73 · 220 · 38 · 1 = 14480 Вт = 14,5 кВт.
Пример 6. Три активных сопротивления Rф1 = 10 Ом, Rф2 = 20 Ом, Rф3 = 5 Ом соединены звездой с нейтральным проводом и присоединены к четырехпроводной трехфазной линии с линейным напряжением Uл = 220В (рисунок 17). Определить: 1) фазные токи Iф1, Iф2, Iф3; 2) ток в нулевом (нейтральном) проводе I0; 3) фазные мощности Рф1, Рф2, Рф3; 4) общую активную мощность трехфазной цепи Р.
Дано: Uл = 220 В, Rф1 = 10 Ом, Rф2 = 20 Ом, Rф3 = 5 Ом.
Определить: Iф1, Iф2, Iф3, Рф1, Рф2, Рф3, Р.
Решение
При наличии нейтрального провода при любой нагрузке (равномерной или неравномерной) справедливо соотношение между фазным Uф и линейным Uл напряжением
Uф = Uл / 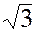 ,
,
Uф = 220/ 1,73 = 127 В.
Помня, что нейтральный провод при любых нагрузках обеспечивает равенство фазных напряжений приемников энергии, получим
Uф = UA= UB= UC= 127 B.
1. Определяем значение фазных (они же линейные) токов по закону Ома:
Iф1 = IA = Uф / Rф1 = 127/10 = 12,7 А;
Iф2 = IB = Uф / Rф2 = 127/20 = 6,35 А;
Iф3 = IC =Uф / Rф3 = 127/5 = 25,4 А.
2. Нагрузка чисто активная, поэтому мощности фаз определяем по тем же формулам, которые применялись в примере 4.
Рф1 = РА = I2ф1Rф1 = 12,72 · 10 = 161,29 · 10 = 1612,9 Вт = 1,613 кВт;
Рф2 = РВ = I2ф2Rф2 = 6,352 · 20 = 806,45 Вт = 0,806 кВт;
Рф3 = РС = I2ф3Rф3 = 25,42 · 5 = 645,16 · 5 = 322,8 Вт = 3,228 кВт.
Активную мощность трехфазной цепи Р определим как сумму мощностей трех фаз:
Р = РА+РВ+РС = 1,613 + 0,806+3,226=5,645 кВт.
Для определения тока в нейтральном проводе при соединении приемников энергии звездой нужно построить векторную диаграмму, придерживаясь такой последовательности как в примере 4:
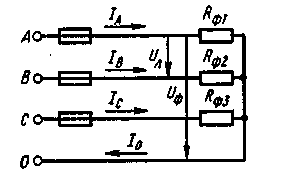
Рисунок 17
1 Выписываем значения вычисленных напряжений и токов: фазные напряжения Uф = UA = UB = UC = 127 B,
фазные (линейные) токи IA = 12,7 A; IB = 6,35 A; IC = 25,4 A.
2 Задаемся масштабом: по напряжению mU = 30 B/см, по току mi = 7 А/см.
3 Определяем длину векторов напряжения и токов:
L 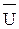 A=L
A=L 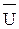 B=L
B=L 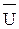 C=Uф / mU = 127 B/30 B/см = 4,23 см;
C=Uф / mU = 127 B/30 B/см = 4,23 см;
LIA = IA / m1 = 12,7 А / 7 А/см = 1,81 см;
LIB = IB / m1= 6,35 A / 7 A/см = 0,9 см;
LIC = IC / m1 = 25,4 А / 7 А/см = 3,62 см.
4 Откладываем векторы фазных напряжений 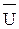 А,
А, 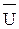 В,
В, 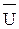 С найденной длины под углом 120 ° относительно друг друга.
С найденной длины под углом 120 ° относительно друг друга.
5 Вдоль векторов фазных напряжений 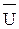 А,
А, 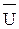 В,
В, 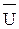 С откладываем векторы фазных токов
С откладываем векторы фазных токов  А,
А,  В,
В,  С, так как нагрузка всех фаз активная
С, так как нагрузка всех фаз активная
(φ = φА = φВ = φС = 0).
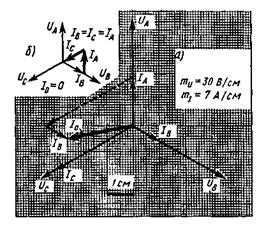
Рисунок 18
6 Геометрическое сложение фазных токов  А,
А,  В,
В,  С производим используя формулу
С производим используя формулу  0 =
0 =  А +
А +  В+
В+  с по правилу многоугольника, которое рассмотрено выше (пример 4), и получим вектор тока в нейтральном проводе (рисунок 18, а).
с по правилу многоугольника, которое рассмотрено выше (пример 4), и получим вектор тока в нейтральном проводе (рисунок 18, а).
На построенной в масштабе векторной диаграмме линейкой измеряем длину вектора тока в нейтральном проводе L 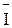 0 и, зная масштаб по току mI, определяем числовое значение I0 : L
0 и, зная масштаб по току mI, определяем числовое значение I0 : L 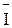 0 = 2,3 см; I0 = L
0 = 2,3 см; I0 = L 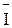 0 m1 = 2,3 см · 7 А/см = 16,1 А.
0 m1 = 2,3 см · 7 А/см = 16,1 А.
Пример 7. Осветительные лампы трех этажей ткацкой фабрики соединены звездой и присоединены к трехфазной четырехпроводной линии с линейным напряжением Uл = 380 В (рисунок 19).
Число ламп на каждом этаже одинаковое n1 = n2 = n3 =50. Мощность каждой лампы Рламп = 100 Вт. Определить: 1) фазные токи IA, IB, IC при одновременном включении всех ламп на каждом этаже; 2) фазные активные мощности РА, РВ, РС и мощность Р всей трехфазной цепи; 3) ответить на вопрос: Чему будет равен ток в нейтральном проводе?
Дано: Uл = 380 В, n1 = n2 = n3 =50 ламп, Рламп = 100 Вт.
Определить: IA, IB, IC, I0, РА, РВ, Рс, Р.
Решение
1. Определяем фазные мощности, исходя из того, что в каждой фазе включено по 50 ламп, мощностью Рламп = 100 Вт каждая:
РА = РВ = РС = n1Pламп = 50 · 100 = 5000 Вт = 5 кВт.
Тогда мощность трехфазной цепи
Р = РА + РВ + РС = 3 · 5 = 15 кВт.
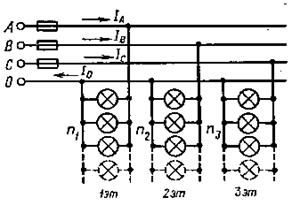
Рисунок 19
2. Фазные (они же линейные) токи найдем из формулы фазной мощности
РА = UфIАcosφA,
предварительно определив
Uф = Uл / 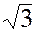 = 380 /1,73 = 220 В,
= 380 /1,73 = 220 В,
cosφA = cosφB = cosφC = 1 - т.к. нагрузка активная.
Тогда Iф = IA = IB = IC = Рф / (Uф cosφф) = 5000 / (220 · 1) = 22,7 А.
3. Для подсчета тока в нулевом проводе построим без масштаба векторную диаграмму (рисунок 18, б). Векторы фазных токов будут иметь одинаковую длину, так как значения токов одинаковые. Направление их векторов - вдоль соответствующих векторов фазных напряжений. Из диаграммы видно, что ток в нейтральном проводе I0 равен нулю.
Рекомендуется решить задачи 4, 5 проверив правильность действий по ответам.
Задача 4. Для схемы (рисунок 14) известны: Rф1 = 110 Ом, Rф2 = 55 Ом, Rф3 = 44 Ом. Линейное напряжение Uл = 220 В.
Определить: фазные значения токов Iф1, Iф2, Iф3, мощности фаз Рф1, Рф2, Рф3; общую активную мощность трехфазной цепи Р.
Ответ: 2 А; 4А; 5А; 440 Вт; 880 Вт; 1100 Вт; 2420 Вт.
Задача 5. Для схемы (рисунок 17) известны Rф1 = 110 Ом, Rф2 = 55 Ом, Rф3 = 44 Ом. Линейное напряжение Uл = 380 В.
Определить: фазные токи IA, IB, IC, мощности фаз РА, РВ, РС; общую активную мощность трехфазной цепи Р.
Ответ: 2 А; 4 А; 5 А; 440 Вт, 880 Вт; 1100 Вт; 2420 Вт.
Указания к решению задачи 3
Для решения задачи 3 необходимо знать материал темы "Электрические машины переменного тока": устройство и принцип действия трехфазного асинхронного двигателя, а также зависимость между электрическими величинами, характеризующими его работу.
Рассмотрим вопрос, знание которого необходимо для решения задачи: зависимость между частотой вращения магнитного поля статора (синхронная частота вращения) n 1 и частотой вращения ротора двигателя n 2.
Частота вращения магнитного поля статора n 1 зависит от числа пар полюсов двигателя p, на которые сконструирована обмотка статора, и от частоты тока трехфазной системы f:
n1 = 60f / p.
Частота тока в цепи (промышленная частота) f = 50 Гц. Тогда формула примет вид
n1= 60 · 50 / p (об/мин).
Из формулы следует, что при любой механической нагрузке, которую может преодолеть двигатель, синхронная частота n1 остается неизменной, так как зависит только от конструкции обмотки статора, т.е. от числа пар полюсов.
Частота вращения n2 связана с частотой вращения n1 характеристикой двигателя. Поэтому частота вращения ротора всегда меньше частоты вращения магнитного поля статора двигателя. С ростом нагрузки двигателя частота вращения n2 немного уменьшается, что приводит к росту скольжения s. Из-за такого неравенства n 2 < n 1 двигатель называется асинхронным. Для нужд производства электродвигатели выпускаются с разной конструкцией обмоток статора, что создает разное число пар полюсов p и, следовательно, разные значения частоты вращения n1. Следует иметь в виду, что при изменении числа пар полюсов p частота вращения n1 изменяется скачкообразно.
Таблица 1
| p | 1 | 2 | 3 | 4 | 5 | 6 |
| n 1, об/мин | 3000 | 1500 | 1000 | 750 | 600 | 500 |
В таблице 1 приведены значения n1, соответствующие числам пар полюсов p, определяемым конструкцией обмотки статора.
Следует иметь в виду, что синхронную частоту вращения двигателя можно определить и без вычисления, а зная только частоту вращения ротора n2, которая по величине близка к ней.
Если, например, n2= 2930 об/мин, то ближайшая из указанного ряда синхронных частот вращения может быть только n1 = 3000 об/мин или для n2 = 490 об/мин синхронная частота вращения двигателя будет n1= 500 об/мин и т.д. Поэтому в паспорте двигателя указывают только значение номинальной частоты вращения ротора n2ном.
По числу полюсов двигателя можно определить синхронную частоту вращения n1. Если, например число полюсов шесть, то число пар полюсов в два раза меньше, т.е. p = 3. По формуле для n1 найдем ее величину
n1 = 3000 / p,
т.к. p = 3, то n1 = 3000 / 3 = 1000 об/мин.
Разберем несколько формул, которые нужно применять при решении задач.
1. Момент вращения М, измеряемый в Н·м, определяется по формуле
М = 9550Р2 / n2
где Р2 - полезная мощность по валу двигателя ( кВт);
n2- частота вращения ротора (об/мин).
При номинальном режиме основные параметры обозначаются:
Мном, Рном = Р2ном, nном = n2ном.
2. Полезная мощность на валу двигателя
Р2 = 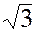 Uл Iл η cosφ
Uл Iл η cosφ
где Uл (В) и Iл (А) – линейные значения напряжения и тока;
η - КПД двигателя в относительных единицах;
cosφ - коэффициент мощности двигателя.
Из этой формулы
Iл = Р2 / ( 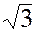 Uл η cosφ.
Uл η cosφ.
3. КПД двигателя
η = Р2 / Р1 → Р1 = Р2 / η,
где Р1(Вт) – активная мощность, потребляемая двигателем из сети, которую можно также определить по формуле
Р1 =  Uл Iл cos φ.
Uл Iл cos φ.
Перед решением задачи следует ознакомиться с решением типовых примеров.
Пример 8. Асинхронный двигатель имеет следующие технические данные для работы в номинальном режиме:
Рном, кВт …………………………………………………………. 3
Uл, В……………………………………………………………….380
nном, об/мин………………………………………………………. 2880
ηном ……………………………………………………………….. 0,85
cosφном……………………………………………………………. 0,88
Число полюсов 2p………………………………………………..2
Определить: 1) номинальное скольжение Sном; 2) мощность Р1ном, потребляемую двигателем из сети; 3) номинальный ток I1ном; 4) номинальный момент вращения Мном.
Дано: Рном= Р2ном=3кВт; Uл = 380 В; nном = n2ном = 2880 об/мин, cosφном = 0,88; ηном = 0,85.
Определить: Sном; Р1ном; I1ном; Мном
Решение
1. Чтобы найти скольжение Sном нужно знать n1 и n2ном. Поэтому предварительно определим синхронную частоту вращения n1 при n2ном = 2880 об/мин. Ближайшая синхронная частота вращения n1 = 3000 об/мин. Такой же результат получим, если воспользуемся формулой для n1. Число полюсов 2. Следовательно, число пар полюсов р = 1. Тогда
n1 = 3000 / р = 3000/1 = 3000 об/мин.
2. Вычислим значение номинального скольжения
Sном = (n1 – n2ном) / n1 = (3000 -2880) / 3000 = 120/3000 = 0,04,
или Sном = 4%.
3. Зная мощность на валу Р2ном и КПД двигателя ηном, найдем мощность Р1ном, которую потребляет двигатель из сети при номинальной нагрузке:
ηном = Р2ном / Р1ном,
откуда: Р1ном = Р2ном / ηном= 3 / 0,85 = 3,35 кВт.
4.Номинальный ток I1ном, потребляемый двигателем из сети, определим, используя формулу для тока
Iл =I1ном = Р2ном /  Uл ηном cosφном = 3000 / (1,73∙380∙0,85∙0,88) = 6,1 А.
Uл ηном cosφном = 3000 / (1,73∙380∙0,85∙0,88) = 6,1 А.
5.Номинальный момент Мном, который развивает двигатель при своей работе:
Мном = 9550 Р2ном / n2ном = 9550∙3 / 2880 = 9,94 Н∙м.
Пример 9. Асинхронный двигатель, работая в номинальном режиме, имеет номинальную частоту вращения ротора n2ном = 490 об/мин. Частота тока питающей сети f = 50 Гц.
Определить: 1) синхронную частоту вращения; 2) скольжение.
Дано: n2ном = 490 об/мин, f = 50 Гц.
Определить: n1, Sном.
Решение
Так как известно, что частота вращения n2ном = 490 об/мин, то ближайшая синхронность частота вращения будет n1 = 500 об/мин.
Найдем номинальное значение скольжения: Sном = (n1 - n2ном) / n1 = (500-490) / 500 = 0,02, или Sном = 2%.
Задача 6. Асинхронный двигатель с короткозамкнутым ротором подключен к сети с напряжением Uл = 380 В и имеет следующие номинальные данные: полезная мощность Р2ном = 4,5 кВт, частота вращения ротора n2ном = 1440 об/мин, КПД ηном= 85,5%, коэффициент мощности cosφном=0,85.
Определить: 1) частоту вращения магнитного поля статора (синхронную частоту вращения) n1; 2) скольжение Sном при номинальном режиме; 3) мощность Р1ном потребляемую двигателем из сети; 4) номинальный момент вращения Мном; 5) номинальный ток двигателя I1ном; 6) суммарные потери мощности в двигателе ΣР.
Ответ: n1 = 1500 об/мин; Sном = 4%; Р1ном = 5,26 кВт, Мном = 29,84 Н∙м; Iном = 9,4 А; Σ Р = 9,76 кВт.
Указания к решению задачи 4
Для решения задачи 4 необходимо знать материал темы "Электрические машины постоянного тока": устройство, принцип действия генераторов и двигателей постоянного тока с параллельным возбуждением, формулы, определяющие параметры таких машин. Используя рисунки 20, 21 разберем основные формулы, необходимые для решения задач.
Генератор с параллельным возбуждением (рисунок 20)
1. ЭДС, наводимая в обмотке якоря,
Е = U + IяRя
где U, В - напряжение на зажимах генератора;
Iя, А – ток якоря;
Rя, Ом – сопротивление обмотки якоря
. 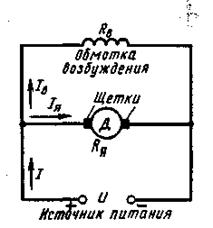
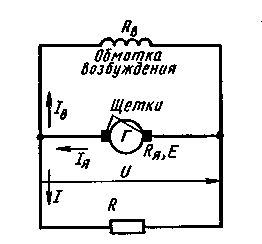
Рисунок 20 Рисунок 21
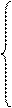 |
якоря Iя = (Е - U) / Rя.
2. Токи возбуждения Iв = U / Rв
нагрузки I = Iя - Iв.
3. Полезная мощность, отдаваемая генератором:
Р2 = U I (Вт).
Мощность Р1, Вт - затраченная первичным двигателем на вращение якоря генератора (потребляемая мощность генератором), определяется из формулы КПД генератора
η = Р2/ Р1 → Р1=Р2/ η.
Двигатель с параллельным возбуждением (рисунок 21)
1. Противо - ЭДС, наводимая в обмотке якоря:
Е = U - IяRя
где U, В - напряжение источника электрической энергии, питающего обмотку якоря;
Iя, А – ток якоря;
Rя, Ом – сопротивление обмотки якоря.
2. Токи якоря, в нагрузке, в обмотке возбуждения:
ток якоря (из формулы противо – ЭДС) Iя = (U - E) / Rя (А)
ток нагрузки I = Iя + Iв
ток в обмотке возбуждения Iв = U / Rв.
где Rв, Ом – сопротивление обмотки возбуждения.
3. Мощность, потребляемая двигателем от источника электрической энергии,
Р1 = U I (Вт);
4. Полезная мощность Р2 на валу двигателя определяется из формулы КПД
η =Р2 / Р1 → Р2 = η Р1 (Вт).
5. Момент вращения двигателя
М = 9550Р2(кВт) / n (об/мин),
где n - частота вращения якоря.
Для лучшего понимания приведенных формул и их применения при решении задач рассмотрим примеры.
Пример 10. Генератор постоянного тока с параллельным возбуждением (рисунок 20), имеющий сопротивление обмотки якоря Rя=0,1Ом и сопротивление обмотки возбуждения Rв=60Ом, нагружен внешним сопротивлением R= 4 Ом. Напряжение на зажимах машины U = 220 В.
Определить: 1) токи нагрузки I, в обмотке возбуждения Iв и в обмотке якоря Iя; 2) ЭДС генератора Е; 3) полезную мощность Р2, расходуемую на нагрузке.
Дано: U = 220 В, Rя = 0,1 Ом; Rв = 65 Ом; R = 4 Ом.
Определить: I, Iв, Iя, Е, Р2.
Решение
1. Ток во внешней цепи
I = U/R = 220/4 = 55A
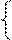 2.Токи: в обмотке возбуждения Iв = U/Rв = 220/65 = 3,38 А;
2.Токи: в обмотке возбуждения Iв = U/Rв = 220/65 = 3,38 А;
в обмотке якоря Iя = I + Iв = 55 + 3,38 = 58,38 А.
3. ЭДС генератора
Е = U + IяRя = 220 + 58,38 ∙ 0,1 = 220 + 5,838 = 225,838 = 225,84 В.
4. Полезная мощность
Р2 = U I = 220 ∙ 55 = 12100 Вт = 12,1 кВт.
Пример 11 Двигатель постоянного тока с параллельным возбуждением подключен к сети с напряжением U = 220 В (рисунок 21). Полезная мощность на валу Р2 = 10кВт, частота вращения якоря n = 2400 об/мин, КПД двигателя η = 80%. Определить: 1) вращающий момент М, который развивает двигатель; 2)поведенную мощность Р1; 3) ток I, потребляемый двигателем из сети; 4) суммарные потери мощности в двигателе ΣР.
Дано: U=220 В, Р2 = 10кВт, η = 80%, n= 2400 об/мин.
Определить: I, M, P1, ΣP.
Решение
1.Момент вращения, который развивает двигатель при данной мощности на валу и частоте вращения:
М = 9550 Р2 / n = 9550 ∙ 10 / 2400 = 39,79 H ∙ м.
2. Потребляемая мощность двигателя из сети
η = Р2 / Р1 → Р1 = Р2 / η = 10 / 0,8 = 12,5 кВт
3. Ток I, потребляемый двигателем из сети (из формулы потребляемой мощности):
Р1 = UI → I = P1 / U = 10000/220 = 45,45 A.
4 Суммарная мощность потерь, зная значения Р1 и Р2;
ΣР = Р1 - Р2 = 12,5 - 10 = 2,5 кВт.
Пример 12 Двигатель постоянного тока с параллельным возбуждением (рисунок 21) работает в номинальном режиме, потребляет ток из сети Iном = 102А при напряжении Uном = 220 В. Сопротивление обмотки возбуждения Rв = 32 Ом. Противо- ЭДС, которая индуцируется в обмотке якоря, Е = 214,9 В.
Определить: 1) ток в обмотке якоря Iя; 2) сопротивление обмотки якоря Rя.
Дано: Uном= 220 В, Iном = 102 А, Rв = 32Ом, Е = 214,9 В.
Определить: Iя, Rя.
Решение
1. Ток в обмотке якоря Iя можно определить по двум формулам:
Iном = Iя+Iв, → Iя = Iном - Iв
или Iя = (U - E) / Rя.
Вторая формула для решения не подходит, так как не известно, Rя.
Чтобы воспользоваться первой формулой, нужно предварительно определить ток в обмотке возбуждения Iв.
2. Зная значение Rв, вычислим ток в обмотке возбуждения:
Iв = U / Rв = 220/32=6,87 А,
тогда
Iя = Iном - Iв = 102 - 6,87 = 95,13 А.
3 По второй формуле для Iя определим сопротивление обмотки якоря
Iя = (U - E) / Rя,
откуда
Rя = (U - E) / Iя =(220 - 214,19) / 95,13 = 0,05 Ом.
Для закрепления знаний методики решения задач рекомендуется решить задачи.
Задача 7. Двигатель постоянного тока с параллельным возбуждением имеет следующие данные: сопротивление обмотки якоря Rя = 0,2 Ом; сопротивление обмотки возбуждения Rв = 40 Ом; КПД генератора η =0,95; ток возбуждения
Iв = 5А, ток в нагрузке I= 95 А.
Определить: 1) электродвижущую силу генератора Е; 2) напряжение на зажимах генератора U; 3) ток в обмотке якоря Iя; 4) полезную мощность генератора Р2; 5) мощность первичного двигателя Р1, затрачиваемую на работу генератора.
Ответ: Е = 220 В; Iя = 100 А; Р2 = 19000 Вт, Р1 = 20000 Вт; U = 220 В.
Задача 8 Двигатель постоянного тока с параллельным возбуждением имеет следующие данные: 1) напряжение сети, питающей двигатель, U= 300 В; 2) ток в обмотке якоря Iя = 100 А; 3) сопротивление обмотки якоря Rя = 0,1 Ом, обмотки возбуждения Rв = 50 ; 4) коэффициент полезного действия двигателя η = 0,9.
Определить: 1) противо- ЭДС Е, наводимую в обмотку якоря при работе двигателя; 2) токи: нагрузки I и в обмотке возбуждения Iв; 3) мощности: полезную на валу двигателя Р2 и потребляемую из сети Р1.
Ответ: Е= 290 В; Iв = 6А; I = 6 А; I = 106 А; Р1 = 31800 Вт; Р2 = 28620 Вт.
Указания к решению задачи 5
В контрольной работе содержание задачи 5 относится к теме "Выпрямители» и включает:
1.Составление схемы одно - или двухполупериодного выпрямителя на полупроводниковых вентилях согласно заданию вашего варианта;
2Подбор полупроводниковых диодов для данной схемы по заданным электрическим параметрам (мощности, току или напряжению);
3Изображение графиков переменного, пульсирующего и постоянного напряжения или тока в нагрузке.
При изучении программного материала темы обратите особое внимание на устройство и работу полупроводниковых диодов, а также на схемы выпрямителей на полупроводниковых вентилях. Рекомендуется также ознакомиться с приводимым описанием.
Структурная схема выпрямителя состоит из трех основных частей: трансформатора, вентиля, сглаживающего фильтра.
Трансформатор – преобразует напряжение переменного тока сети до напряжения переменного тока, необходимого нагрузке.
Вентиль ( диод ) – преобразует напряжение переменного тока нагрузки в пульсирующее напряжение.
Сглаживающий фильтр необходим для преобразования пульсирующего напряжения в напряжение постоянного тока, необходимого нагрузке.
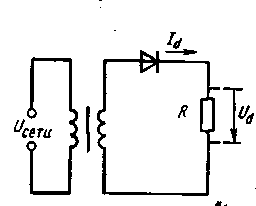 В контрольной работе в схемах выпрямления сглаживающий фильтр можно не изображать(Рисунок22)
В контрольной работе в схемах выпрямления сглаживающий фильтр можно не изображать(Рисунок22)
Рисунок 22
Полупроводниковые диоды обладают односторонней проводимостью электрического тока в интервалах температур от - 60° до + 75°С - для германиевых диодов и - 60° до + 150° С - для кремниевых и поэтому применяются в качестве электрических вентилей. При более высоких температурах полупроводниковые диоды теряют свойство односторонней проводимости и в качестве вентилей их применять нельзя.
Полупроводниковые диоды подбираются для схем выпрямления по двум параметрам: 1) допустимый ток в прямом направлении Iдоп; 2)значение допустимого напряжения, действующее на диод в обратном направлении, когда диод закрыт, Uобр.. Эти параметры для диодов приводятся в справочниках, выписка из которых приведена в таблице 2 и используется для решения задач.
Таблица 2
| Тип диода | I доп, А | U обр, В | Тип диода | I доп, А | U обр, В |
| Д205 Д207 Д209 Д210 Д211 Д214 Д214А Д214Б Д215 Д215А Д215Б Д223 Д233Б Д234Б Д242 Д242А Д242Б Д244А Д244Б Д302 | 0,4 0,1 0,1 0,1 0,1 5 10 2 5 10 2 10 5 5 5 10 2 10 2 1 | 400 200 400 500 600 100 100 100 200 200 200 500 500 600 100 100 100 50 50 200 | Д243 Д243А Д243Б Д217 Д218 Д221 Д222 Д224 Д224А Д224Б Д226 Д226А Д231 Д231Б Д232 Д232Б Д244 Д303 Д304 Д305 | 5 10 2 0,1 0,1 0,4 0,4 5 10 2 0,3 0,3 10 5 10 5 5 3 3 6 | 200 200 200 800 1000 400 600 50 50 50 400 300 300 300 400 400 50 150 100 50 |
| |
Значение обратного напряжения на диодах (Uв) рассчитывается по формулам в зависимости от выпрямленного напряжения постоянного тока (Ud) и схем выпрямления.
В контрольной работе, для всех схем выпрямления, согласно своему варианту, необходимо сначала рассчитать выпрямленный ток или выпрямленное напряжение.
По заданным значениям мощности потребителя ( Р ) и выпрямленного тока ( Id) находят выпрямленное напряжение(Ud) :
Ud = P / Id
или наоборот, по заданному выпрямленному напряжению ( Ud) и мощности ( Р) находят выпрямленный ток:
Id = P / Ud
Далее необходимо подобрать диоды для заданных схем выпрямления своего варианта:
Однофазная однополупериодная схема – имеет один диод (Рисунок 22), который пропускает ток в течение одного полупериода ( положительный полупериод )
В отрицательный полупериод диод заперт, и ток не пропускает.
Во время отрицательного полупериода диод находится под действием обратного напряжения:
Uв = π Ud = 3,14 Ud
По справочнику (таблица 2 ) подбирают диоды по двум параметрам:
1 Допустимый ток диода должен быть равен или больше выпрямленного тока
Iдоп ≥ Id
2 Допустимое напряжение на диоде в отрицательный полупериод должно быть равно или больше обратного напряжения, т е
Uобр. ≥ Uв ≥ π Ud.
3 Изобразить однополупериодную схему выпрямления и графики переменного, пульсирующего и постоянного напряжения или тока в нагрузке.
Однофазная двухполупериодна схема с выведенной средней точкой вторичной обмотки трансформатора – имеет два диода(Д1 и Д2), которые пропускают ток в разные полупериоды (Рисунок 23).

Рисунок 23
Во время отрицательного полупериода диоды находятся под действием обратного напряжения:
Uв = π Ud = 3,14 Ud
По справочнику (таблица 2) подбирают диоды по двум параметрам:
1Допустимый ток диода должен быть равен или больше половины выпрямленного тока, т е:
Iдоп д . ≥ 0,5Id
2 Допустимое напряжение на диоде в отрицательный полупериод должно быть равно или больше обратного напряжения, т е:
Uобр. ≥ Uв ≥ π Ud
3 Изобразить двухполупериодную схему выпрямления и графики переменного, пульсирующего и постоянного напряжения или тока в нагрузке
Однофазная мостовая схема – имеет четыре диода, которые пропускают ток парами ( Д1 и Д3 или Д2 и Д4 ) в разные полупериоды.

Рисунок 24
Во время отрицательного полупериода диоды находится под действием обратного напряжения:
Uв = 1,57 Ud
По справочнику (таблица 2) подбирают диоды по двум параметрам:
1Допустимый ток диода должен быть равен или больше половины выпрямленного тока, т е:
Iдоп д. ≥ 0,5Id
2 Допустимое напряжение на диоде в отрицательный полупериод должно быть равно или больше обратного напряжения, т е:
Uобр д ≥ Uв ≥ 1,57 Ud
3 Изобразить мостовую схему выпрямления и графики переменного, пульсирующего и постоянного напряжения или тока в нагрузке.
Расчет различных схем выпрямления рассмотрим в примерах:
Пример 13 Для питания постоянным током потребителя мощностью P = 250Вт при напряжении Ud=100B необходимо собрать схему однополупериодного выпрямления (Рисунок 22), подобрав диоды, технические данные которых приведены в таблице 2.
Дано: P = 250 Вт; Ud = 100 B.
Определить Выбрать тип, начертить схему выпрямителя.
Решение
1 Определим ток потребителя Id из формулы мощности
P = Ud Id → Id = P / Ud = 250/100 = 2,5 A.
2 Найдем напряжение, действующее на диод в непроводящий период Uв, для такой схемы:
Uв = πUd = 3,14 ∙ 100 = 314 B.
3 По данным Id = 2,5 A и Uв = 314В, в таблице 2 подберем диод, исходя из условий
Iдоп ≥ Id и Uобр ≥ Uв.
Таким будет диод Д232Б(5А, 400В), у которого Iдоп = 5 А > Id = 2,5 A и
Uобр = 400 В > Uв = 314 В.
4Чертим схему и графики переменного, пульсирующего и постоянного напряжения или тока в нагрузке.
Пример 14 Для питания постоянным током Id = 10А потребителя мощностью P = 1000Вт необходимо собрать схему двухполупериодного выпрямления с выводом от средней точки вторичной обмотки трансформатора (Рисунок 23), подобрав диоды, технические данные которых приведены в таблице 2. Начертить схему выпрямителя.
Дано: P =1000 Вт; Id = 10А.
Определить: Выбрать тип диодов. Начертить схему выпрямителя.
Решение
1 Определим напряжение потребителя Ud из формулы мощности
P = Ud Id → Ud = P / Id = 1000/10 = 100В.
2 Определим напряжение, действующее на диод в непроводящий период Uв, для такой схемы
Uв = πUd = 3,14 ∙ 100 = 314 B.
3По данным Id = 10 A и Uв = 314B, в таблице 2 подберем диод
Д232Б(5А, 400В), у которого Iдоп.д = 5А = 0,5 Iо = 0,5 ∙ 10 = 5A и
Uобр = 400 В > Uв = 314 В.
4Чертим схему и графики переменного, пульсирующего и постоянного напряжения или тока в нагрузке
Пример 15 Для питания постоянным током потребителя мощностью Р = 800 Вт при напряжении Ud = 150 B необходимо собрать мостовую схему двухполупериодного выпрямления (Рисунок 24), подобрав диоды, технические данные которых приведены в таблице 2.
Дано: P = 800 Вт; Ud = 150 B.
Определить: Выбрать тип диодов, начертить схему выпрямителя.
Решение
1 Определим ток потребителя из формулы мощности
P = Ud Id → Id = P / Ud = 800/150 = 5,33 A
2 Найдем напряжение, действующее на диод в непроводящий период, Uв для мостовой схемы:
Uв = 1,57 Ud = 1,57 ∙ 150 = 235,5 В.
3 По данным, Id = 5,33 A и Uв = 235,5 В, в таблице 2 выбираем тип диода, исходя из условий Iдоп.д. ≥ 0,5 Id и Uобр ≥ Uв.
Таким будет диод Д231Б(5А, 300В), у которого Iдоп.д = 5 А > 0,5 Iо = 0,5 ∙ 5,33 = 2,56 А и Uобр = 300 В > Uв = 235,5 В.
4Чертим схему и графики переменного, пульсирующего и постоянного напряжения или тока в нагрузке
Для закрепления материала рекомендуется решить задачи, к которым даны ответы для возможности самопроверки.
Задача 9 От выпрямителя необходимо получить напряжение постоянного тока Ud=80B при мощности P= 800 Вт. Схема выпрямителя однополупериодная (рисунок 22). Подобрать диод для такой схемы, используя данные таблицы 2.
Ответ: диод Д231(10А, 300В).
Задача 10 От двухполупериодной схемы выпрямления с выводом от средней точки вторичной обмотки трансформатора (рисунок 23) необходимо получить напряжение постоянного тока Ud = 100 B при мощности P = 1000 Вт. Используя данные таблицы 2 подобрать типы диодов.
Ответ: диоды Д232Б(5А, 400В).
Задача 11 Двухполупериодная однофазная мостовая схема дает напряжение постоянного тока Ud = 100 В при мощности P = 1000 Вт. Диоды в схеме (рисунок 24) вышли из строя. Используя данные таблицы 2 подобрать типы диодов для такой схемы.
Ответ: диоды Д215(5А, 200В).
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
Задача 1
Цепь постоянного тока со смешанным соединением состоит из четырех резисторов. В зависимости от варианта заданы: схема (рисунок 1- 20) сопротивления резисторов R1, R2, R3, R4; напряжение "U", ток "I" или мощность "Р" всей цепи. (таблица 3)
Определить: 1) эквивалентное сопротивление цепи Rэкв;
2) токи, проходящие через каждый резистор I1, I2, I3, I4;
3) рассчитать баланс мощностей схемы.
4) как изменится сила тока в цепи "I", если перегорит одно
из сопротивлений (подтвердить расчетом).
Таблица 3
| Ва-риант | Схема | R 1 , Ом | R 2 , Ом | R 3 , Ом | R 4 , Ом | I, U, P. А, B , Вт | Перегорит сопротивле-ние |
| 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5 6 7 8 9 10 | 3 15 12 6 20 10 30 50 10 4 16 4 5 2 12 30 3 30 7 11 15 10 20 7 25 2 12 40 3 10 | 4 10 2 30 40 15 20 40 11 2 40 6 6 1 4 6 15 20 3 90 20 90 10 60 15 3 4 20 10 2 | 2 4 4 6 30 35 4 60 90 20 10 2 12 15 2 60 20 3 72 10 40 6 2 15 10 1 4 25 30 40 | 3 15 4 20 5 15 2 12 10 5 8 24 6 10 4 30 40 5 90 5 3 60 5 4 12 3 2 5 20 10 | U=20B I=5A P=50Вт U=100B I=2A P=48Вт U=40B I=3A Р=120Вт U=40B I=4A Р=90Вт U=60B I=25A P=200Вт U=100B I=4A Р=320Вт U=150B I=4A Р=100Вт U=120B I=20A Р=90Вт U=120B I=25A P=200Вт U=40B I=3A Р=80Вт | R2 R3 R2 R3 R1 R3 R4 R2 R4 R3 R2 R4 R3 R1 R3 R1 R2 R1 R3 R2 R1 R4 R3 R4 R3 R1 R3 R4 R3 R4 |
Схема для контрольной работы к задаче 1



| 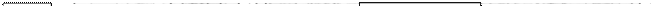 |










Задача 2, Варианты 01 - 15
Пролеты цеха рыбокомбината, где установлены три конвейера по переработке рыбы, освещаются одновременно светильниками с лампами накаливания. Лампы соединены звездой с нейтральным проводом и получают питание по четырехпроводному кабелю от трансформаторной подстанции с линейным напряжением - Uл. Лампы первого конвейера включены между фазой А и нейтральным проводом, второго конвейера - между фазой В и нейтральным проводом, третьего - между фазой С и нейтральным приводом. Светильники каждого конвейера имеют одинаковое число ламп, соответственно nA = nB = nC (рисунок 5.21). Определить величины, которые не заданы в условиях вашего варианта:
1) линейное напряжение - Uл (UAB=UBC=UCA);
2) фазное напряжение - Uф (UA, UB, UC);
3) фазные токи - Iф (IA, IB, IC);
4) мощность одной лампы - Рламп;
5) фазные мощности - Рф (РА, РВ, РС)
6) общую мощность трехфазной цепи - Р
Данные для своего варианта взять из таблицы 4.
Таблица 4
| Вариант | Число ламп nA=nB=nC | P, U, I | Вариант | Число ламп nA = nB = nC | P, U, I |
| 1 | 11 | Рламп=200Вт Uл=380В | 9 | 22 | Рф=2200Вт Iф=10А |
| 2 | 11 | Рламп=200Вт Iф=10А | 10 | 22 | Рф=6600Вт Uф=220В |
| 3 | 11 | Рламп=200Вт Uф=220В | 11 | 55 | Рламп=40Вт Uф=220В |
| 4 | 11 | Рф=2200Вт Iф=10А | 12 | 55 | Рламп=40Вт Uл=380В |
| 5 | 11 | Рф=2200Вт Uл=380В | 13 | 55 | Рламп=40Вт Iф=10А |
| 6 | 22 | Рламп=100Вт Uл=380В | 14 | 55 | Рф=2200Вт Uл=380В |
| 7 | 22 | Рламп=100Вт Iф=10А | 15 | 55 | Рф=2200Вт Uф=220В |
| 8 | 22 | Рламп=100Вт Uф=220В |

Рисунок21
Задача 2, Варианты 16-30
Для нагрева водного раствора в ванне моечной установки, предназначенной для мойки блоков цилиндров двигателей внутреннего сгорания и деталей автомобилей, используются трубчатые электронагревательные элементы (ТЭН). Нагреватели соединены треугольником и подключены к трехпроводной кабельной линии, которая получает питание от распределительного пункта цеха с линейным напряжением - Uл = 220 В (рисунок 5.22). Нагреватели первого приемника - nAB подключены между фазами А и В, второго - nBC между фазами В и С, третьего - nCA между фазами С и А. В каждой фазе включено одинаковое число ТЭН nAB=nBC=nCA. Определить величины, которые не заданы в условиях задачи вашего варианта:
1) фазные токи - Iф (IAB, IBC, ICA);
2) линейные токи - Iл (IA, IB, IC);
3) мощность одного нагревателя - Рнагр;
4) фазные мощности - Рф (РАВ, РВС, РСА);
5) активную мощность трехфазной цепи - Р.
Данные взять из таблицы 5
Таблица 5
| Вариант | Число ТЭН nAB=nBC=nCA | Р, Рф, Рнагр, Вт | Вариант | Число ТЭН nAB=nBC=nCA | Р, Рф, Рнагр, Вт |
| 16 17 18 19 20 21 22 23 | 3 2 3 2 3 4 6 4 | Рнагр=220 Рф=440 Рф=660 Р=1320 Р=1980 Рф=880 Рнагр=110 Р=2640 | 24 25 26 27 28 29 30 | 6 5 6 5 12 5 12 | Рф=660 Рнагр=110 Р=1980 Рф=550 Рнагр=55 Р=1650 Р=1980 |

Рисунок 22
Задача 3, Варианты с 01 по 30
Трехфазные асинхронные двигатели используются для работы строгальных, фрезеровальных и токарных станков металлообрабатывающего завода. Все двигатели работают в номинальном режиме и подключены к сети с линейным напряжением Uл = 380В, с промышленной частотой f=50 Гц. Известны число полюсов и некоторые данные режима их работы: номинальная мощность - Рном, частота вращения ротора - n2ном, скольжение - Sном, коэффициент мощности - cosφном и коэффициент полезного действия - ηном. Определить величины, не заданные в условии:
1) частоту вращения магнитного поля статора n1;
2) частоту вращения ротора - n1;
3) скольжение - Sном;
4) ток двигателя - I1ном;
5) номинальный момент вращения - Мном;
6) активную мощность, потребляемую двигателем из сети - Р1ном.
7) Объяснить, как осуществляется регулирование частоты вращения ротора двигателя.
Данные для своего варианта взять из таблицы 6
Таблица 6
| Вариант | Число полюсов | Р2ном, кВт | S ном , % | n 2ном , об/мин | cosφ ном | η ном |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | 6 6 6 6 6 6 6 6 6 8 8 8 10 10 10 10 10 10 10 12 12 12 12 8 8 4 4 4 8 8 | 45 35 37 55 20 30 75 35 55 37 45 110 20 75 45 70 100 25 37 45 30 75 90 45 75 37 75 45 5,5 5,5 | 4,4 4,4 4,4 4,4 4,4 4,4 4,4 4,4 4,4 2,0 2,0 2,0 1,5 3,5 2,5 | 580 590 585 570 490 485 490 480 735 730 1460 1470 1480 735 730 | 0,89 0,88 0,87 0,89 0,88 0,89 0,90 0,91 0,88 0,89 0,84 0,85 0,92 0,89 0,92 0,92 0,91 0,89 0,92 0,91 0,89 0,91 0,94 0,91 0,89 0,93 0,84 0,86 0,81 0,92 | 0,92 0,93 0,94 0,93 0,93 0,94 0,95 0,93 0,93 0,90 0,91 0,90 0,80 0,92 0,94 0,89 0,92 0,91 0,89 0,94 0,92 0,89 0,88 0,89 0,92 0,82 0,84 0,85 0,92 0,81 |
Задача 4, Варианты с 01 по 15
Генератор постоянного тока с параллельным возбуждением приводится в работу асинхронным двигателем трехфазного тока и используется для питания специальной аппаратуры предприятия. Сопротивление обмотки якоря Rя = 0,1 Ом, возбуждения Rв = 50 Ом. КПД генератора η=0,9. Начертить схему генератора параллельного возбуждения. Определить значения, характеризующие работу генератора, которые не заданы в условиях задачи:
1) ЭДС генератора - Е;
2) напряжение на зажимах генератора - U;
3) значение токов в нагрузке - I, в обмотке якоря Iя, в обмотке возбуждения - Iв;
4) полезную мощность, отдаваемую генератором - Р2;
5) мощность, затраченную электродвигателем на работу генератора - Р1.
Данные для своего варианта взять из таблицы 7.
Таблица 7
| Вариант | Е, U , P , I | Вариант | T , U , P , I |
| 1 2 3 4 5 6 7 8 | U=220B; Iя =100А Е=210В; Iя = 100А I= 96A; U = 200B P2=19200Вт; I = 96A P2=19200Вт; Iв = 4A Р1=21330Вт; I=96A P1=21330Вт; Iв = 4А Iв =4А; Iя = 100А | 9 10 11 12 13 14 15 | U = 200B, I=96A E =210B; U =200B E = 260B; U =250B U=250B; I=95A Iв =5А; Iя = 100А Р1=26388Вт; Iв =5А Р1 =26388Вт; I=95A |
Задача 4, Варианты с 16 по 30
Двигатель постоянного тока с параллельным возбуждением общепромышленного применения используется для приведения в движение центробежного насоса, который откачивает воду из траншей, предназначенных для прокладки телефонных кабелей. Сопротивление обмотка якоря Р2=0,1 Ом, возбуждения Rв=55 Ом, КПД двигателя η=0,85, частота вращения якоря n= 956 об/мин. Начертить схему двигателя. Определить значения, характеризующие работу двигателя, которые не указаны в условиях задачи:
1) противо-ЭДС, Е, которая индуцируется в обмотке якоря при работе двигателя;
2) напряжение сети, от которой питается двигатель, U;
3) момент вращения двигателя, М;
4) токи в обмотке якоря Iя, в обмотке возбуждения Iв, общий ток двигателя I;
5) мощности: на валу двигателя Р2 и потребляемую из сети Р1.
Данные для своего варианта взять из таблицы 8.
Таблица 8
| Вариант | Е, U , P , I | Вариант | Е, U , P , I |
| 16 17 18 19 20 21 22 23 | U=220B; Iя =100А Е=210В; Iя = 100А I= 104A; U = 220B P2=1944Вт; I = 104A P2=1944Вт; Iв = 4A Р1=22880Вт; I=104A P1=22880Вт; Iв = 4А Iв =4А; Iя = 100А | 24 25 26 27 28 29 30 | U = 200B, I=104A E =210B; U =220B E = 265B; U =275B U=275B; I=105A Iв =5А; Iя = 100А Р1=288758Вт; Iв =5А Р1 =288758Вт; I=275A |
Задача 5, Варианты с 1 по 30
От выпрямителя, согласно данной вам схеме (таблица 9) потребителю подается выпрямленное напряжение - Ud или ток - Id при мощности - Р. Подберите по таблице 10 полупроводниковые диоды по допустимому току (Iдоп) и обратному напряжению (Uобр), для работы в качестве вентилей. Начертите схему выпрямителя и опишите процесс выпрямления переменного тока в ней (достоинства и недостатки) поясните ответ графиками переменного, пульсирующего и постоянного напряжения или тока в нагрузке.
Таблица 9
| Вари-ант | схема | U0 или I0 | Р, Вт | Вари-ант | схема | U 0 или I 0 | Р, Вт |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | Однополупериодная | 1 А 100 В 8 А 50 В 10 А 20 В 4 А 200 В 3 А 100 В 50 В 4 А 40 В 10 А 80 В | 30 Вт 1000 800 400 60 100 240 20 450 50 500 120 400 200 400 | 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | вторичной обмотки трансформатора | 25 В 8 А 90 В 0,2 А 0,8 А 100 В 20 А 50 В 80 В 30 В 10 А 100 В 4 А 30 В 150 В | 250 400 450 20 64 800 1000 500 400 300 400 200 200 240 300 |
| 2-х полупериодная с выведен ной средней точкой | 2-х полупериод-ная мостовая схема |
Таблица 10
| Тип диода | I доп, А | U обр, В | Тип диода | I доп, А | U обр, В |
| Д 205 Д 207 Д 209 Д 210 Д 211 Д 214 Д 214А Д 214Б Д 215 Д 215А Д 215Б Д 233 Д 233Б Д 234Б Д 242 Д 242А Д 242Б Д 244А Д 244Б Д 302 | 0,4 0,1 0,1 0,1 0,1 5 10 2 5 10 2 10 5 5 5 10 2 10 2 1 | 400 200 400 500 600 100 100 100 200 200 200 500 500 600 100 100 100 50 50 200 | Д 243 Д 243А Д 243Б Д 217 Д 218 Д 221 Д 222 Д 224 Д224А Д 224Б Д 226 Д 226А Д 231 Д 231Б Д 232 Д 232Б Д 244 Д 303 Д 304 Д 305 | 5 10 2 0,1 0,1 0,4 0,4 5 10 2 0,3 0,3 10 5 10 5 5 3 3 6 | 200 200 200 800 1000 400 600 50 50 50 400 300 300 300 400 400 50 150 100 50 |
ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
По данной дисциплине выполняется одна контрольная работа из 5-ти задач, исходные данные которых составлены на 30 вариантов. Номер варианта определяется двумя последними цифрами личного дела (шифра) студента. Например: номера личных дел 13,50, 35, номера вариантов соответственно: 13; 20; 05, т.е. [(50-30=20) и (35-30=05)] и т.д. Работы, выполненные, не по своему варианту не засчитываются и возвращаются студенту.
Дата: 2019-03-05, просмотров: 352.