f(x1,x2,…,xn)ÎSÛf(x1,x2,…,xn)=f*(x1,x2,…,xn)=Øf(`x1,`x2,…,`xn).
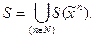
Докажем, что класс самодвойственных функций замкнут. Замкнутость класса самодвойственных функций следует из принципа двойственности:
Пусть 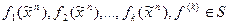 и
и 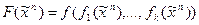 . Определим двойственную к F функцию:
. Определим двойственную к F функцию:
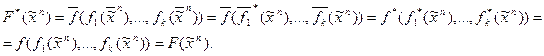
Следовательно, класс самодвойственных функций замкнут. Для произвольной булевой функции, заданной суперпозицией над некоторым множеством булевых функций, существует двойственная формула, имеющая то же строение, в которой все вхождения функций заменены двойственными функциями.
Чтобы определить число самодвойственных функций n переменных, рассмотрим способ их построения. Он состоит в том, что в верхней части таблицы рассматриваемых функций необходимо записать все возможные двоичные векторы длины 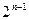 . Число таких векторов равно числу размещений с повторениями из 2 по
. Число таких векторов равно числу размещений с повторениями из 2 по 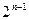 , т.е.
, т.е. 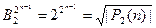 . Отсюда мощность класса самодвойственных функций равна
. Отсюда мощность класса самодвойственных функций равна
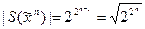 .
.
Можно показать, что не существует самодвойственных элементарных булевых функций, существенно зависящих от двух переменных. К классу самодвойственных относятся функции 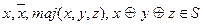 .
.
Неполнота класса самодвойственных функций следует из существования не самодвойственных функций.
Лемма о не самодвойственной функции: Если f(x1,x2,…,xn) ÏS, то отождествлением переменных и подстановкой в нее самодвойственных функций х и `х можно получить не самодвойственную функцию – константу 0 или 1.
ª Пусть 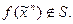 Тогда найдется набор значений переменных
Тогда найдется набор значений переменных 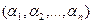 такой, что
такой, что 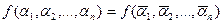 . Выполним подстановку в данную функцию самодвойственной функции
. Выполним подстановку в данную функцию самодвойственной функции 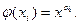 Полученную суперпозицию запишем в виде:
Полученную суперпозицию запишем в виде:
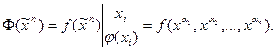
Далее определим значения Ф(x) при х=1.
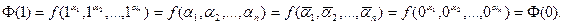 ¨
¨
Таким образом, получена не самодвойственная функция – константа. Используя функцию отрицания, можно получить другую константу. Рассмотрим примеры «работы» леммы над не самодвойственной функцией.
Пример1. 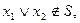 так как f(01)=f(10)=1. Произведем указанную в лемме подстановку, выбрав набор (0,1). Тогда
так как f(01)=f(10)=1. Произведем указанную в лемме подстановку, выбрав набор (0,1). Тогда 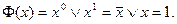
Пример 2. 
Тогда  .
.
Пример 3. Пусть функция задана вектором (1011 1001). Здесь наборы с номерами 3 и 4 являются противоположными, и 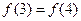 . МДНФ для этой функции имеет вид
. МДНФ для этой функции имеет вид
 .
.
Выполним подстановку значений переменных на наборах 3 и 4 в формулу.
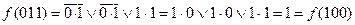
Таким образом, получена константа 1. Из наборов с номерами 1 и 6 можно получить константу 0.
Класс монотонных функций М
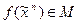 тогда и только тогда, когда на наборах значений переменных, находящихся в отношении предшествования, значения функции находятся в отношении £:
тогда и только тогда, когда на наборах значений переменных, находящихся в отношении предшествования, значения функции находятся в отношении £:
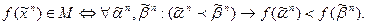
Два булевых вектора 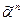 и
и 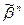 находятся в отношении предшествования тогда и только тогда, когда одноименные координаты этих векторов находятся в отношении £:
находятся в отношении предшествования тогда и только тогда, когда одноименные координаты этих векторов находятся в отношении £: 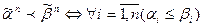 . например, в случае трех переменных наборы их значений имеют номера от 0 до 7. Соответственно отношение предшествования на этих наборах определяется так:
. например, в случае трех переменных наборы их значений имеют номера от 0 до 7. Соответственно отношение предшествования на этих наборах определяется так: 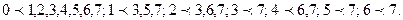
Отношение предшествования на множестве Bn при n³2 является частичным порядком. Мажоритарная функция 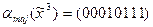 в соответствии с определением является монотонной, а трехместная функция XOR – нет,
в соответствии с определением является монотонной, а трехместная функция XOR – нет, 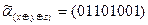 .
.
Множество всех монотонных функций определим как 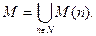
Теорема. Класс М замкнут и неполон, т.е. [M]=M¹P2.
ª Так как тождественная функция монотонна, для доказательства замкнутости достаточно показать, что суперпозиция монотонных функций монотонна. Пусть ФÎP2(m), fiÎP2(n), i=1,2,…,m. Докажем, что 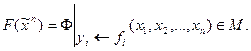
Возьмем два произвольных набора значений переменных таких, что 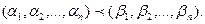 Тогда
Тогда
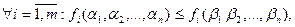
и, следовательно,
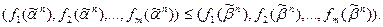
А так как  то монотонность
то монотонность  доказана, а значит, доказана и замкнутость класса М. Неполнота М следует из существования немонотонных функций. ¨
доказана, а значит, доказана и замкнутость класса М. Неполнота М следует из существования немонотонных функций. ¨
Лемма о немонотонной функции: из произвольной немонотонной функции с помощью подстановки констант и отождествления переменных можно получить функцию отрицания.
ª Пусть  Это означает, что существуют такие наборы значений переменных, находящихся в отношении предшествования, что
Это означает, что существуют такие наборы значений переменных, находящихся в отношении предшествования, что 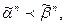 а
а 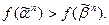 Последнее означает, что
Последнее означает, что 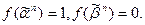 Из того, что значения функции на выбранных наборах не равны, следует, что сами наборы также не равны. Пусть расстояние Хемминга между наборами равно 1 и обусловлено различием значений переменной
Из того, что значения функции на выбранных наборах не равны, следует, что сами наборы также не равны. Пусть расстояние Хемминга между наборами равно 1 и обусловлено различием значений переменной 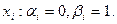 Образуем функцию
Образуем функцию 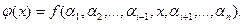 Тогда
Тогда  Так как функция не монотонна, то
Так как функция не монотонна, то
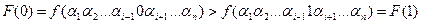 .
.
Соотношение 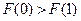 определяет одноместную функцию отрицания.
определяет одноместную функцию отрицания.
Если  , то следует найти в множестве промежуточных наборов два таких соседних набора, на которых происходит нарушение монотонности. После этого задача сводится к предыдущему примеру.
, то следует найти в множестве промежуточных наборов два таких соседних набора, на которых происходит нарушение монотонности. После этого задача сводится к предыдущему примеру.
Пример применения леммы о немонотонной функции. Рассмотрим элементарную булеву функцию ®, вектор значений которой имеет вид: 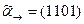 . Это двуместная функция, нулевой набор предшествует второму, расстояние Хемминга между ними равно 1 по первой переменной и
. Это двуместная функция, нулевой набор предшествует второму, расстояние Хемминга между ними равно 1 по первой переменной и 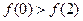 . Вторая переменная в обоих наборах равна 0, а первая принимает оба возможных значения (мелькает). «Работа» леммы над этой функцией представлена ниже:
. Вторая переменная в обоих наборах равна 0, а первая принимает оба возможных значения (мелькает). «Работа» леммы над этой функцией представлена ниже:
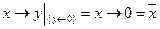 .
.
В соответствии с леммой из немонотонной функции получена одноместная функция отрицания.
¨
Класс линейных функций L
Произвольная булева функция может быть представлена полиномом по mod2 в виде суммы по mod2 монотонных конъюнкций (полинома Жегалкина). Пусть 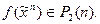 Говорят, что функция f линейна, если ее полином Жегалкина не содержит конъюнкций, ранг которых превышает 1 и имеет вид
Говорят, что функция f линейна, если ее полином Жегалкина не содержит конъюнкций, ранг которых превышает 1 и имеет вид
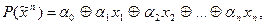 где коэффициенты
где коэффициенты  . Такая функция называется симметрической.
. Такая функция называется симметрической.
Множество всех линейных функций обозначается 
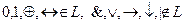
Терема. Класс L замкнут и неполон, т.е. [L]=L¹P2.
ª Так как тождественная функция линейна, то для доказательства замкнутости класса L достаточно показать, что суперпозиция линейных функций есть линейная функция. Доказывается записью соответствующей суперпозиции. Неполнота L следует из существования нелинейных функций. ¨
Очевидно, что мощность класса n-местных линейных функций равна |L(n)|=2n+1.
Лемма о нелинейной функции. Из произвольной нелинейной функции с помощью подстановки констант, тождественной функции и функции отрицания и, возможно, навешиванием отрицания на всю функцию, можно получить конъюнкцию и дизъюнкцию.
Пусть 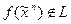 . Тогда ее полином по mod2 содержит монотонные элементарные конъюнкции ранга выше 1. Выберем среди этих элементарных конъюнкций конъюнкцию минимального ранга (>=2). Для удобства рассуждений положим, что выбранная конъюнкция содержит переменные x1 и x2. Выполним следующие подстановки: всем переменным, участвующим в выбранной конъюнкции, кроме переменных x1 и x2, присвоим значение1. А всем переменным, не вошедшим в выбранную конъюнкцию, присвоим значение 0. В силу единственности полинома, представляющего данную функцию, после выполнения равносильных преобразований полином примет вид:
. Тогда ее полином по mod2 содержит монотонные элементарные конъюнкции ранга выше 1. Выберем среди этих элементарных конъюнкций конъюнкцию минимального ранга (>=2). Для удобства рассуждений положим, что выбранная конъюнкция содержит переменные x1 и x2. Выполним следующие подстановки: всем переменным, участвующим в выбранной конъюнкции, кроме переменных x1 и x2, присвоим значение1. А всем переменным, не вошедшим в выбранную конъюнкцию, присвоим значение 0. В силу единственности полинома, представляющего данную функцию, после выполнения равносильных преобразований полином примет вид:
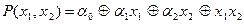 .
.
Полином содержит три коэффициента (  ) . Каждому набору значений коэффициентов соответствует своя собственная функция. Следовательно, таких функций будет восемь. Для определения всех функций, порождаемых нелинейной функцией заданного вида, построим таблицу.
) . Каждому набору значений коэффициентов соответствует своя собственная функция. Следовательно, таких функций будет восемь. Для определения всех функций, порождаемых нелинейной функцией заданного вида, построим таблицу.
| a0 a1 a2 | Полином | Функция |
| 000 | x1x2 | F(x1x2)=x1x2 |
| 001 | x2Åx1x2= 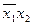
| 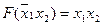
|
| 010 | 
| 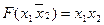
|
| 011 | 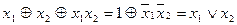
| 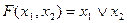
|
| 100 | 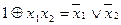
| 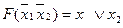
|
| 101 | 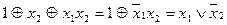
| 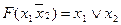
|
| 110 | 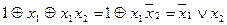
| 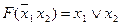
|
| 111 | 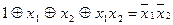
| 
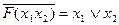
|
Доказано, что из нелинейной функции могут быть получены конъюнкция и дизъюнкция.
Теорема Поста
Теорема. Чтобы множество DÍP2 было функционально полным в P2, необходимо и достаточно, чтобы среди функций этого множества нашлась хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна не самодвойственная функция, хотя бы одна немонотонная и хотя бы одна нелинейная функции.
Следствие 1. В любом функционально полном в Р2 множестве существует функционально полное подмножество, состоящее не более, чем из пяти функций.
Следствие 2. В любом функционально полном множестве существует функционально полное подмножество, состоящее не более чем из четырех функций.
Для доказательства функциональной полноты системы булевых функций по критерию Поста необходимо построить таблицу Поста, строки которой именуются функциями исследуемой системы, а столбцам присваиваются имена предполных классов. На пересечении i-й строки и j-го столбца таблицы ставится 1, если i-я функция принадлежит j-му классу, и 0 – в противном случае. Система функций полна, если в каждом столбце таблицы имеется хотя бы один 0. В противном случае система не является функционально полной в Р2, так как входит целиком в один из предполных классов.
Пусть имеется система функций D={(x1Å x2Åx3 ), (x1®x2), (x1&`x2) , 1}. Таблица Поста для нее будет иметь вид:
| T0 | T1 | S | M | L | |
| f1={(x1Å x2Åx3 ) | 1 | 1 | 1 | 0 | 1 |
| f2=(x1®x2) | 0 | 1 | 0 | 0 | 0 |
| f3=(x1&`x2) | 1 | 0 | 0 | 0 | 0 |
| f4=1 | 0 | 1 | 0 | 1 | 1 |
Согласно критерию Поста система функций D функционально полна, так как в каждом столбце имеется хотя бы один 0. Критерии вхождения функции в предполные классы описаны выше.
Другой вопрос, связанный с использованием теоремы Поста, состоит в определении минимально необходимого набора функций из множества D, образующих функционально полную систему. Система функций D ÍР2 называется базисом в Р2, если она функционально полна в Р2, но при исключении из нее любой функции, она перестает быть функционально полной, т.е. [D]=P2, и "f:((fÎD)®([D\{f}]ÌP2)). Для определения базиса, соответствующего данной системе D, используют метод Петрика, состоящий в следующем. Рассматривая функции системы D как переменные, строим из них конъюнктивную нормальную форму, содержащую пять (по числу предполных классов) элементарных дизъюнкций, включая в каждую элементарную дизъюнкцию только те функции системы, которые принадлежат данному предполному классу, и соединяя полученные дизъюнкции связкой &. Затем преобразуем полученное выражение к ДНФ, использую аксиомы и тождества логики высказываний. Каждая из конъюнкций в полученной ДНФ содержит все функции, образующие базис. Длина ДНФ соответствует числу базисов, соответствующих данной системе. Для рассмотренного примера применение метода Петрика состоит в следующем:
(f2Úf4)&f3&(f2Úf3Úf4)&(f1Úf2Úf3)&(f2Úf3)=(f2Úf4)&f3=f2f3 Ú f3f4.
Таким образом, данная система содержит два базиса: D1= {f2,f3 }, D2={f3, f4}.
Теорема Поста позволяет также определить, можно ли из данного множества булевых функций получить некоторую функцию методом суперпозиций. Рассмотрим, например, можно ли получить симметрическую функцию трех переменных суперпозициями над мажоритарной функцией трех переменных. Построив таблицу Поста, убедимся в невозможности этого, так как m(x3) сохраняет 0, 1, самодвойственная, монотонная и нелинейная, а симметрическая трехместная функция сохраняет 0, 1, самодвойственная, не монотонная и линейная. В тоже время, добавив к мажоритарной функции функцию голосования, получим функционально полную в Р2 систему, позволяющую согласно теореме Поста получить любую булеву функцию, в том числе и искомую. В этом можно убедиться, выполнив соответствующие преобразования.
Список литературы
1. Ерусалимский Я.М. Дискретная математика: теория задачи, приложения. – М.: «Вузовская книга», 1999. – 280 с.
2. Лавров И.А., Л.Л. Максимова. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: издательство «Наука», 1975. – 240 с. (и более поздние издания этой книги).
3. Г.П. Гаврилов, А.А. Сапоженко. Сборник задач по дискретной математике. М.: издательство «Наука», главная редакция физико-математической литературы. 1977 г. 368 с.
4. С.П. Плеханов. Симметричные карты - мощное средство минимизации булевых функций при проектировании цифровых устройств больших размерностей.// Электронная техника. Сер. 10. Микроэлектронные устройства. Вып. 4(88), 1991
Дата: 2019-03-05, просмотров: 507.