Электрическое колебание, которое описывается гармоническими (sin и cos) функциями времени, называется гармоническим. Такое колебание можно записать S (t) = A_m cos (ωt – φ).

Здесь A_m – амплитуда, ωt – φ = θ(t) – фаза. Величину ω = 2πf = 2π/T называют угловой частотой. Гармонические колебания в радиоэлектронике занимают исключительное место благодаря:

- простоте технической реализации генератора;

- неизменности формы гармонических колебаний при прохождении через линейную цепь с постоянными параметрами (меняется только амплитуда и фаза).

Гармоническое колебание полностью характеризуется двумя величинами: амплитудой A_m и фазой θ. Как известно, аналогичными величинами определяется положение вектора на плоскости. Используя эту аналогию, гармоническое колебание можно условно изображать вектором на плоскости.

Наряду с векторным представлением гармонические колебания можно представлять комплексными числами. Как известно, комплексное число

a + jb = A_m e^jα = A_mcos(α) + jA_msin(α)

полностью характеризуется модулем A_m и аргументом α, аналогичными амплитуде и фазе гармонического колебания. Комплексное число Á_m = A_me ^­jφ называют комплексной амплитудой гармонического колебания.

Метод расчета цепей, базирующихся на понятии комплексной амплитуды, называют методом комплексных амплитуд. Метод комплексных амплитуд в электротехнике впервые в 1883 году применил немецкий ученый Ч.Штейнмец. В России этот метод широко использовал академик В.Ф. Миткевич.

Переход от временной функции к комплексной амплитуде обратим: S ( t ) = A_mcos ( ωt – φ ) Û 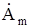. Очевидно, что при всех математических преобразованиях, где вещественная и мнимая части комплексного числа преобразуются независимо одна от другой, этот метод может быть использован без каких-либо ограничений. Примерами таких математических операций, называемых линейными, являются сложение, вычитание, умножение на постоянную величину, дифференцирование и интегрирование.

Операции умножения и деления являются нелинейными. Для получения правильного результата приходится использовать искусственный прием: один из переменных множителей брать комплексно сопряженным. Примером может служить нахождение мощности переменного тока по формуле P =IUcos(φ)=Re 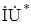. Практически важным случаем нелинейной операции является введение комплексных изображений для сопротивлений. Учитывая закон Ома 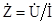, найдем символические изображения для простых случаев чисто активного, чисто емкостного и чисто индуктивного сопротивлений.

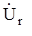      = R .

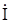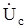      = 1/C 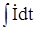= (1/jωC) · i_me^jωt = (1/jωС)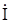

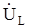      = L di/dt = L d(i_me^jωt)/dt = jωLi_me^jωt = jωL .

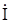Из этих соотношений непосредственно следуют выражения для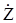

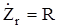
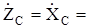                              1/jωС = ( 1/j ) X_C

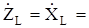                             jωL = jX_L .

Следует особо подчеркнуть, определение комплексных изображений для сопротивлений включает в себя нелинейную операцию 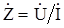. Поэтому соотношение между сопротивлением и его комплексным изображением имеет другой характер, чем в случае тока и напряжений. Сопротивление равно не вещественной или мнимой части, а модулю своего символического изображения.