Задание для домашней контрольной работы представлено в 10 вариантах. Каждый вариант задания состоит из 5 задач. Обучающийся должен выполнить все задачи своего варианта. Номер варианта выбирается по личному шифру обучающегося (согласно номеру в списке журнала для учебных занятий). Если в контрольной работе 10 вариантов, то номеру варианта соответствует последняя цифра шифра, цифра «0» соответствует 10-му варианту. Работы, не соответствующие своему варианту, не засчитываются и возвращаются обучающемуся без проверки.
К выполнению домашней контрольной работы можно приступать только тогда, когда соответствующая тема изучена согласно методическим указаниям, приведённым в данном пособии.
Домашняя контрольная работа оформляется в отдельной тетради или на листах А4. На титульном листе указывается наименование образовательной организации; вид работы; название учебной дисциплины; номер варианта; Ф.И.О. обучающегося; номер его учебной группы; Ф.И.О. преподавателя, проверяющего работу; год выполнения.
Образец оформления
Областное государственное бюджетное профессиональное
образовательное учреждение
«Смоленский политехнический техникум»
Домашняя контрольная работы
по учебной дисциплине
«Математика»
Вариант №2
Выполнил: студент
группы Эз 2-18
Бобылев М.В.
Проверил: преподаватель
Абрамова Г.М.
2018 г.
Методические указания по выполнению 1 задачи каждого варианта
Литература:
1.Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 –с. 229 – 242.
2. Дадаян А.А. Математика: Учебник. - М.: ФОРУМ: ИНФРА-М, 2005. – с.490-507с.
Основные формулы:
Комплексным числом называется число вида a + bi, где a и b – действительные числа, а число i , определяемое равенством 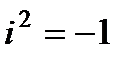 , называется мнимой единицей:
, называется мнимой единицей:
1. Два комплексных числа 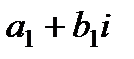 и
и 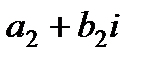 называются равными, если
называются равными, если 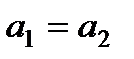 ;
; 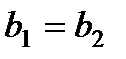
2. Суммой двух комплексных чисел 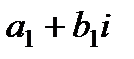 и
и 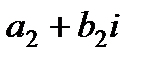 называется комплексное число
называется комплексное число 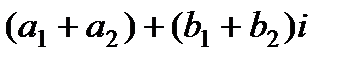
3. Произведением двух комплексных чисел 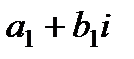 и
и 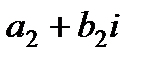 называется комплексное число
называется комплексное число 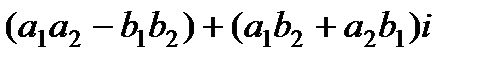
Комплексные числа 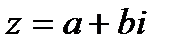 и
и 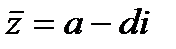 называются сопряженными.
называются сопряженными.
Произведение сопряженных комплексных чисел 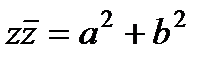 – число действительное и неотрицательное.
– число действительное и неотрицательное.
Комплексное число 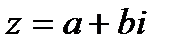 можно изображать точкой плоскости с координатами
можно изображать точкой плоскости с координатами 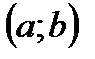 ; а также вектором
; а также вектором 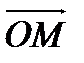 с началом в точке
с началом в точке 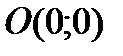 и концом в точке
и концом в точке 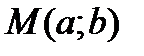 (cмотри рисунок).
(cмотри рисунок).
| a |
| a |
| a |
| a |
| a |
| a |
| a |
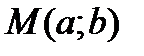
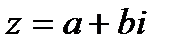
|
| y |
| x |
| 0 |
| b |
Число 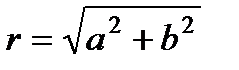 называется модулем комплексного числа.
называется модулем комплексного числа. 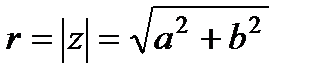
Угол φ между положительным направлением оси Ох и вектором 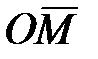 , называется аргументом комплексного числа. Для числа
, называется аргументом комплексного числа. Для числа 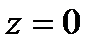
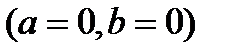 аргумент не определен.
аргумент не определен.
Из определения тригонометрических функций следует, что если φ - аргумент комплексного числа  , то имеют место равенства
, то имеют место равенства 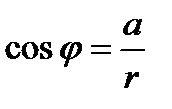 ,
, 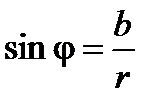 ,
, 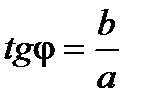
Комплексное число можно записывать в различных формах:
 - алгебраическая форма комплексного числа;
- алгебраическая форма комплексного числа;
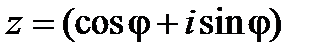 - тригонометрическая форма комплексного числа;
- тригонометрическая форма комплексного числа;
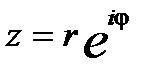 - показательная форма комплексного числа.
- показательная форма комплексного числа.
Образец решения типовой задачи:
Решить квадратные уравнения:
1. 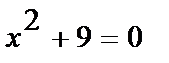 ,
, 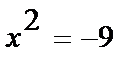 ,
, 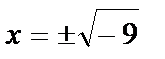 ,
, 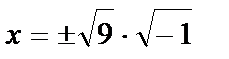 ,
, 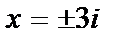 . Ответ:
. Ответ: 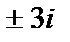 .
.
2. 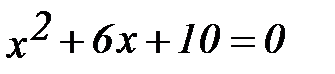
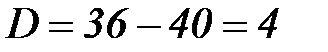

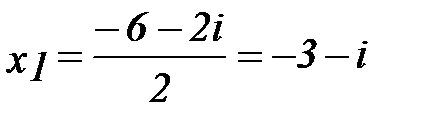
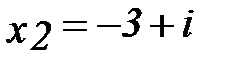
Представить в тригонометрической и показательной форме числа:
1) 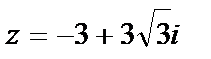 . Решение:
. Решение: 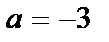 ,
, 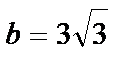 . Значит,
. Значит, 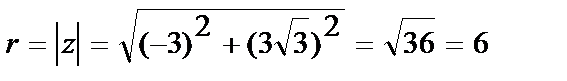 . Найдем
. Найдем 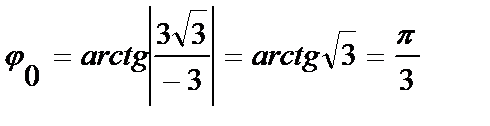 . Поскольку
. Поскольку 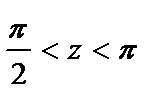 , т. к.
, т. к. 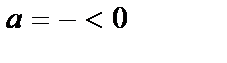 и
и  , то
, то 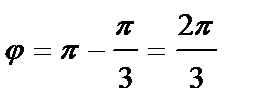 . Поэтому,
. Поэтому,  – тригонометрическая форма комплексного числа,
– тригонометрическая форма комплексного числа, 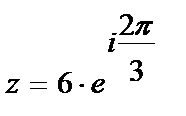 – показательная форма комплексного числа.
– показательная форма комплексного числа.
Методические указания по выполнению 2 задачи каждого варианта
Литература:
1. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 –с.92-104.,188-277.
2. Дадаян А.А. Математика: Учебник. - М.: ФОРУМ: ИНФРА-М, 2005. –с.275-359.
3. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов Н/Д: Феникс 2011. – с.47-158.
Основные формулы:
Приведем основные теоремы, на которых основано вычисление пределов:
Если существуют 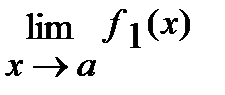 и
и 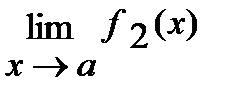 , то
, то
а)  ,
,
б) 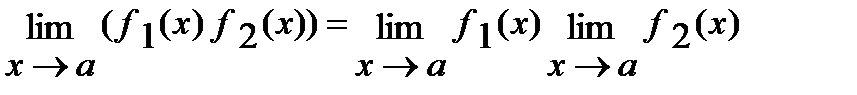
в) 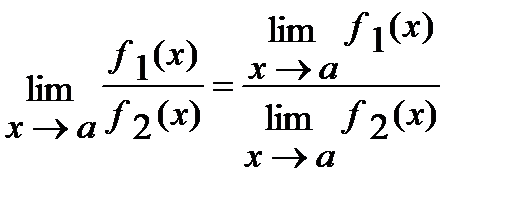 , если
, если  .
.
Первый замечательный предел:
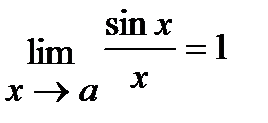
Второй замечательный предел:
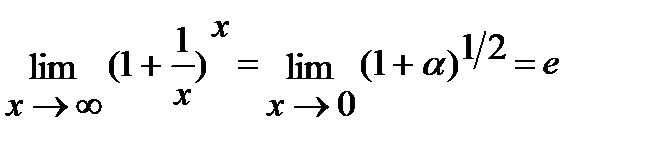
Образец решения типовой задачи:
Найдите пределы:
1. 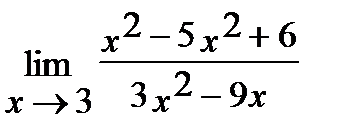 ; 2.
; 2. 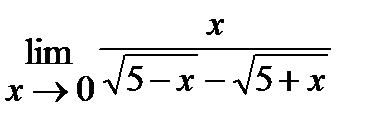 ;
;
3. 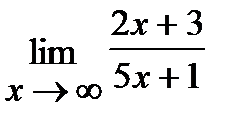
Решение 1.
Пределы числителя и знаменателя при х → 3 равны нулю. Разложим квадратный трехчлен в числителе на линейные множители по формуле 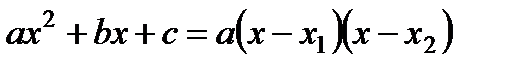 , где х1 и х2 – корни трехчлена. Разложив на множители и знаменатель, сократим дробь на
, где х1 и х2 – корни трехчлена. Разложив на множители и знаменатель, сократим дробь на 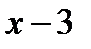 . Получим
. Получим
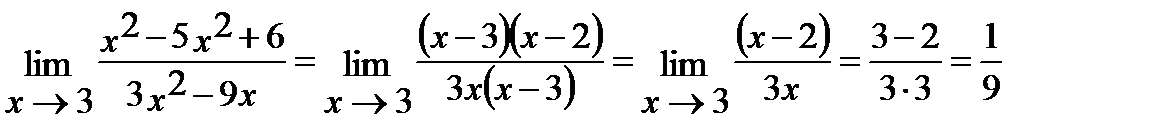
Решение 2.
Пределы числителя и знаменателя при х → 0 равны нулю. Умножив числитель и знаменатель на сопряженный знаменателю множитель 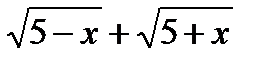 и затем, сократив дробь на х, получим:
и затем, сократив дробь на х, получим:
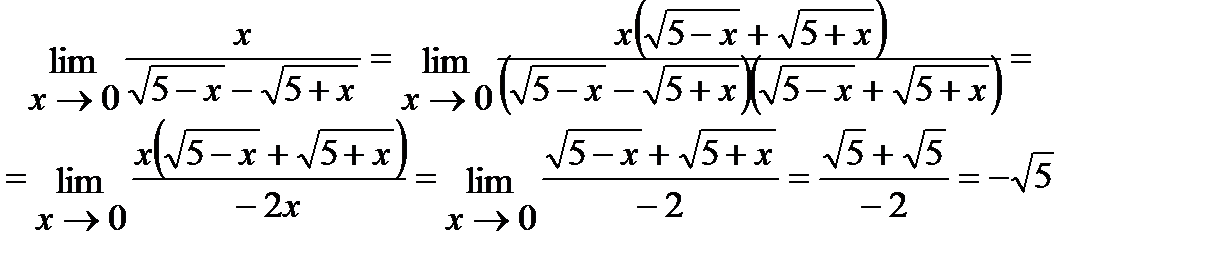
Решение 3.
При х → ∞ числитель и знаменатель – величины бесконечно большие. Разделим числитель и знаменатель на х (на наивысшую степень аргумента в знаменателе).
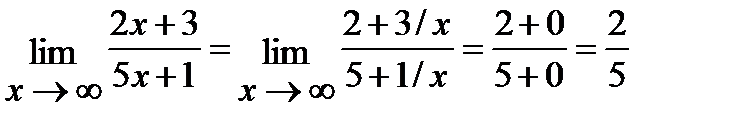 .
.
Методические указания по выполнению 3 задачи каждого варианта
Литература:
1. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 –с.92-104.,188-277.
2. Дадаян А.А. Математика: Учебник. - М.: ФОРУМ: ИНФРА-М, 2005. –с.275-359.
3. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов Н/Д: Феникс 2011. – с.47-158.
Основные формулы:
Общая схема исследования функции и построение ее графика.
Найдите область определения функции.
Исследуйте функцию на четность или нечетность, на периодичность.
Найдите промежутки знакопостоянства; выясните поведение функции на концах промежутка знакопостоянства.
Найдите промежутки монотонности функции, ее экстремумы.
Найдите промежутки выпуклости графика функции, ее точки перегиба.
Постройте график функции, используя полученные результаты исследования.
Образец решения типовой задачи:
Построить график функции: 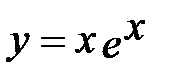 ;
;
D(y)=R
Функция не является четной и нечетной, не периодична.
у = 0 при х = 0. Два промежутка знакопостоянства (-∞;0) и (+∞;0). Для x 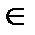 (-∞;0) y<0, для x
(-∞;0) y<0, для x 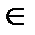 (+∞;0) y>0. Рассмотрим поведение функции на концах промежутков:
(+∞;0) y>0. Рассмотрим поведение функции на концах промежутков: 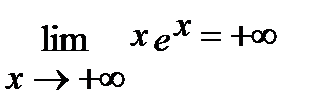
 (по правилу Лопиталя).
(по правилу Лопиталя).
Найдем производную данной функции:
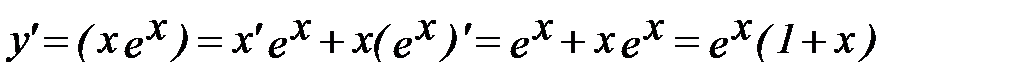
y′=0 при х = - 1, эта точка делит область определения функции на два промежутка (-∞;-1) и (-1;+∞)
| -1 |
Исследуемая функция в промежутке xЄ(-∞;-1) убывает, а для xЄ(-1;+∞) - возрастает точка х = - 1 – точка минимума 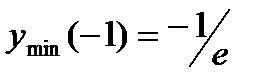 .
.
Найдем вторую производную функции:

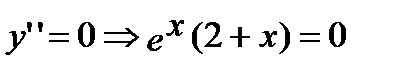 при х=-2
при х=-2
| 2 |
для 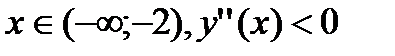 , следовательно, график функции на этом интервале выпуклый вверх.
, следовательно, график функции на этом интервале выпуклый вверх.
Для 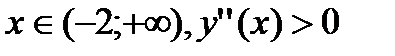 следовательно, график функции на данном интервале выпуклый вниз.
следовательно, график функции на данном интервале выпуклый вниз.
По полученным данным строим график функции:
| х |
| (-2;-2/е²) (-1;-1/е) |
| y |
Методические указания по выполнению 4 задачи каждого варианта
Литература:
1. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 –с.92-104.,188-277.
2. Дадаян А.А. Математика: Учебник. - М.: ФОРУМ: ИНФРА-М, 2005. –с.275-359.
3. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов Н/Д: Феникс 2011. – с.47-158.
Основные формулы:
Формула Ньютона-Лейбница для вычисления определенного интеграла:
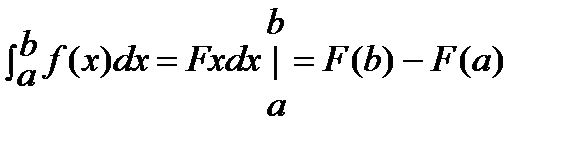
Площадь криволинейной трапеции, ограниченной непрерывной кривой y=f(x), двумя прямыми х = а и х = b и отрезком a≤x≤b на оси абсцисс, вычисляется с помощью определенного интеграла по формулам:
1.

|
| S |
2.
| S |
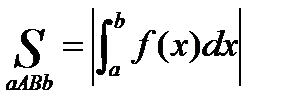
|
3.
f(x)=0 =>x=c
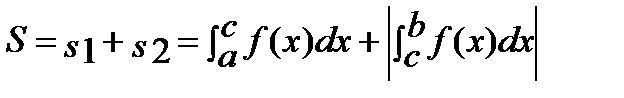
|
| S11 |
| S |
4.
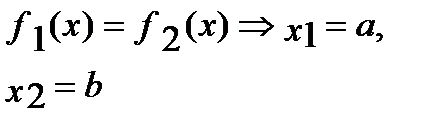
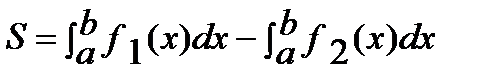
|
| S |
5.
y=f(x)=>x=  (y) (y)
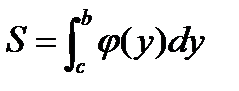
|
| S |
Образец решения типовой задачи:
Пример.
Вычислите площадь фигуры, ограниченной линиями y=-x²-2x+3 , осями координат и прямой х = 2.
Построим данные линии:
| y=-x²-2x+3 |
Найдем точки пересечения графика функции с осью Ох:
y=-x²-2x+3
-x²-2x+3=0
x²+2x-3, x1=1, x2=-3
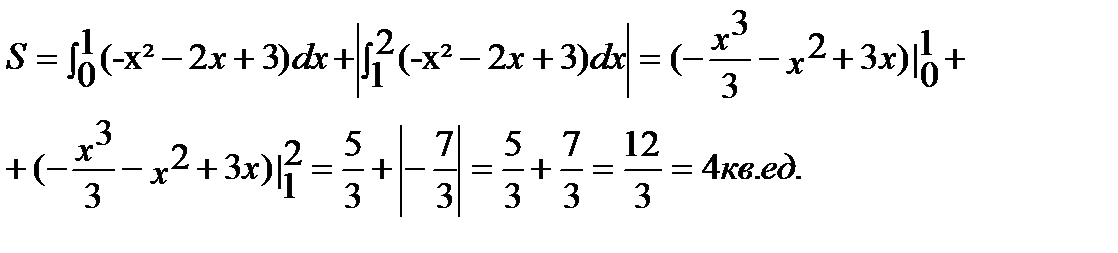
Методические указания по выполнению 5 задачи каждого варианта
Литература:
1. Богомолов Н.В. Практические занятия по математике. – М: Высшая школа, 2003 –с.92-104.,188-277.
2. Дадаян А.А. Математика: Учебник. - М.: ФОРУМ: ИНФРА-М, 2005. –с.275-359.
3. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов Н/Д: Феникс 2011. – с.47-158.
Основные формулы:
Основные понятия комбинаторики
Размещения
Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, содержащее по m элементов, называется размещением из n элементов по m (0≤m≤n).
Число размещений из n элементов по m элементов в каждом обозначают  и вычисляют по формуле
и вычисляют по формуле 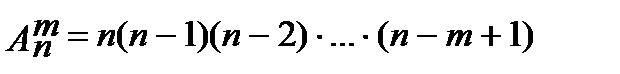 или формулу можно записать в другом виде:
или формулу можно записать в другом виде: 
Считаем, что 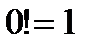 .
.
Перестановки
Размещения из n элементов по n элементов называются перестановками из n элементов (частный случай размещения).
Число перестановок из n элементов данного множества обозначают Pn и вычисляют по формуле Pn=123...n=n! .
Сочетания
Подмножество из m элементов, составленное на множестве из n элементов, называется сочетанием из n элементов по m элементов. Число подмножеств по m элементов в каждом, содержащихся во множестве из n элементов, обозначают 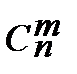 и вычисляют по формуле
и вычисляют по формуле 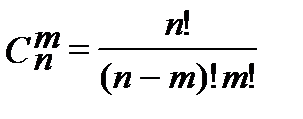
Случайные события. Вероятность события
Случайное событие – событие, связанное с данным испытанием, которое при осуществлении испытания может произойти, а может и не произойти. События обозначаются большими латинскими буквами (A, B…)
Событие в данных условиях называется достоверным, если в результате опыта оно непременно произойдет, и невозможным, если оно заведомо не произойдет.
Говорят, что несколько событий в данном опыте образуют полную систему событий, если в результате опыта непременно должно произойти хотя бы одно из них.
Числовая мера степени объективной возможности события – это вероятность события. Вероятность события А обозначается Р(А).
Пусть из систем n несовместных равновозможных исходов испытания m исходов благоприятствуют событию А, тогда вероятностью события А называют отношение m числа исходов, благоприятных событию А, к числу всех исходов данного испытания: Р(А) = m/n. Эта формула носит название классического определения вероятности.
Если В – достоверное событие, то m = n и Р(В) = 1.
Если С – невозможное событие, то m = 0 и Р(С) = 0.
Если А – случайное событие, то m≤n и Р(А) ≤1 .
Таким образом, вероятность события заключается в следующих пределах: 0≤P(A) ≤1
Образец решения типовой задачи:
Задача.
В партии из 24 деталей 5 бракованных. Из партии выбирают наугад 6 деталей. Найдите вероятность того, что среди этих 6 деталей 2 окажутся бракованными (событие В).
Решение
Число равновозможных независимых исходов равно: 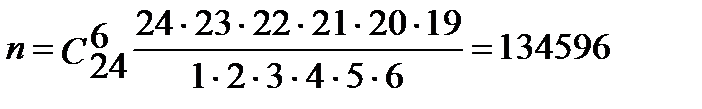
Подсчитаем число m-исходов, благоприятных событию В. Среди 6 взятых наугад деталей 2 бракованных и 4 стандартных. Две бракованные можно выбрать из 5: 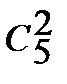 способами, а 4 стандартных – из 19:
способами, а 4 стандартных – из 19: 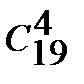 способами.
способами.
Каждая комбинация бракованных может сочетаться с каждой комбинацией стандартных деталей, поэтому: 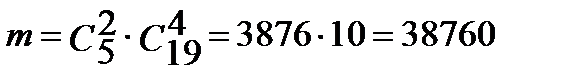
Следовательно: 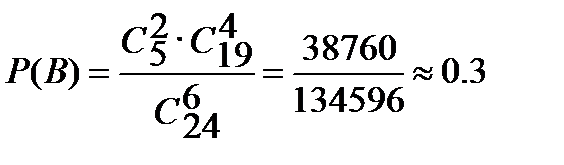 .
.
ЗАДАНИЕ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
Задача № 1. Решить квадратное уравнение, изобразить его решения на
плоскости:
1. 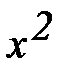 + 2х + 5 = 0
+ 2х + 5 = 0
2. 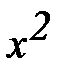 – 6х + 18 = 0
– 6х + 18 = 0
3. 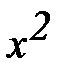 – 4х + 5 = 0
– 4х + 5 = 0
4. 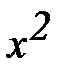 – 10х + 41 = 0
– 10х + 41 = 0
5. 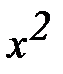 - 2х + 10 = 0
- 2х + 10 = 0
6. 2 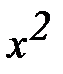 – 2х + 5 = 0
– 2х + 5 = 0
7. 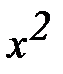 – 4х + 13 = 0
– 4х + 13 = 0
8. 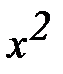 + 4х + 13 = 0
+ 4х + 13 = 0
9. 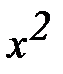 + 2х + 17 = 0
+ 2х + 17 = 0
10. 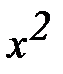 – 6х + 13 = 0
– 6х + 13 = 0
Задача № 2. Найдите пределы функций:
1. а)  , б)
, б) 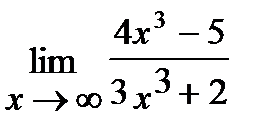
2. а) 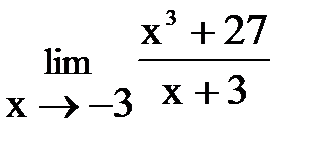 , б)
, б) 
3. а)  , б)
, б) 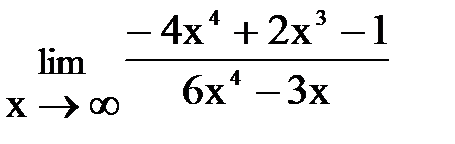
4. а) 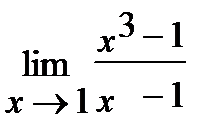 , б)
, б) 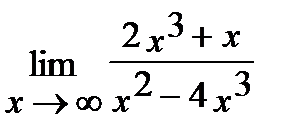
5. а) 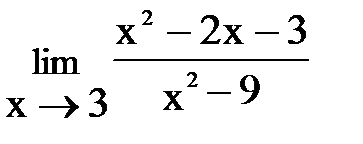 , б)
, б) 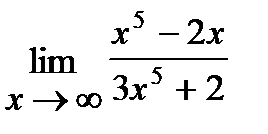
6. а)  , б)
, б) 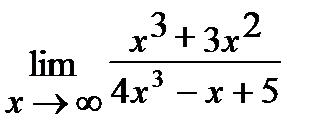
7. а) 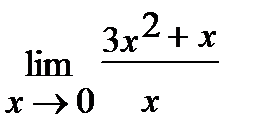 , б)
, б) 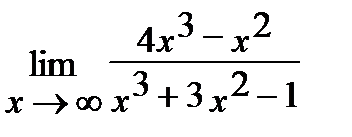
8. а) 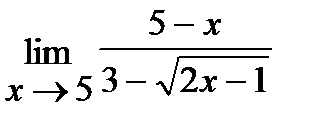 , б)
, б) 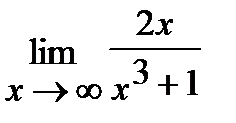
9. а) 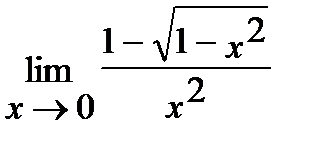 , б)
, б) 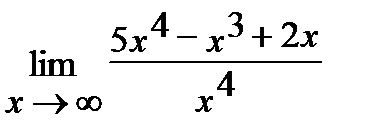
10. а) 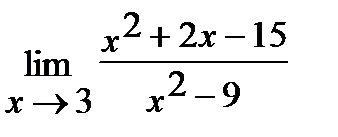 , б)
, б) 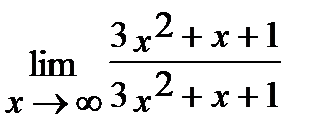
Задача № 3. Исследуйте функцию и постройте ее график:
1. 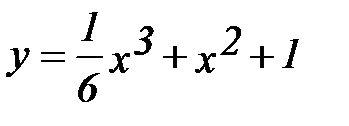 6.
6. 
2. 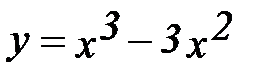 7.
7. 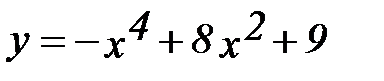
3. 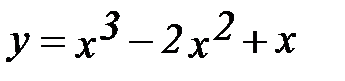 8.
8. 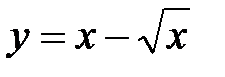
4. 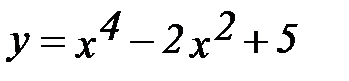 9.
9. 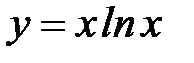
5. 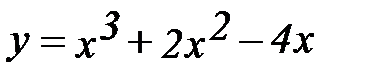 10.
10. 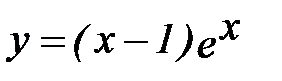
Задача № 4. Вычислите площадь фигуры, ограниченной линиями,
используя определенный интеграл. Сделайте чертеж.
1. y=x² и y³=x 6. x-y-5=0, 2x-3y-6=0, y=0;
2. y=x²-x, y=0, x=0, x=2 7. y=x²+1, x=0,x=2,y=0
3. y=x²-4x, y=0, x=0, x=5 8. y=5x-x²+6, y=0
4. y=x²+2, y=2x+2 9. y=6x-x²-5, y=0
5. x+2y+1=0, x+y-5=0, y=0 10. y=-x²+4x, y=0
Задача № 5
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 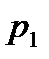 для первого сигнализатора и
для первого сигнализатора и  для второго. Найти вероятность того, что при аварии:
для второго. Найти вероятность того, что при аварии:
а) сработает хотя бы один;
б) сработает только один;
Значение параметров 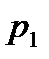 и
и  для вариантов следующие:
для вариантов следующие:
Первый вариант 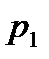 = 0,95,
= 0,95,  = 0,9. Второй вариант
= 0,9. Второй вариант 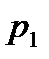 = 0,9,
= 0,9,  = 0,85.
= 0,85.
Третий вариант 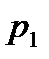 = 0,95,
= 0,95,  = 0,85. Четвертый вариант
= 0,85. Четвертый вариант 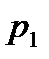 = 0,85,
= 0,85,  = 0,8.
= 0,8.
Пятый вариант 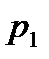 = 0,9,
= 0,9,  = 0,8. Шестой вариант
= 0,8. Шестой вариант 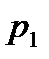 = 0,75,
= 0,75,  = 0,85.
= 0,85.
Седьмой вариант 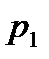 = 0,9,
= 0,9,  = 0,75. Восьмой вариант
= 0,75. Восьмой вариант 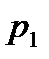 = 0,95,
= 0,95,  = 0,75.
= 0,75.
Девятый вариант 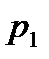 = 0,7,
= 0,7,  = 0,75. Десятый вариант
= 0,75. Десятый вариант 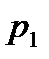 = 0,95,
= 0,95,  = 0,7.
= 0,7.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К
ДИФФЕРЕНЦИРОВАННОМУ ЗАЧЁТУ
1. Определение комплексного числа, геометрическое изображение комплексного числа, модуль и аргумент.
2. Алгебраическая форма комплексного числа. Действия над комплексными числами в алгебраической форме.
3. Тригонометрическая форма комплексного числа. Действия над комплексными числами в тригонометрической форме.
4. Показательная форма комплексного числа. Действия над комплексными числами в показательной форме.
5. Понятие предела функции в точке. Непрерывность функции. Основные теоремы о пределах.
6. Понятие производной функции в точке, ее геометрический и физический смысл.
7. Использование производной для исследования функции на монотонность, экстремумы, выпуклость графика, точки перегиба.
8. Понятие неопределенного интеграла и его свойства.
9. Непосредственное интегрирование и замена переменной в неопределенном интеграле.
10. Определенный интеграл, его вычисление. Геометрический смысл определенного интеграла.
11. Понятие функции нескольких переменных. Частные производные функции нескольких переменных.
12. Понятие дифференциального уравнения, порядок дифференциального уравнения, дифференциальные уравнения с разделяющимися переменными. Общее и частное решения дифференциального уравнения.
13. Понятие однородного, однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
14. Понятие простейшего дифференциального уравнения в частных производных дифференциального уравнения линейного относительно частных производных.
15. Понятие числового ряда, сходимость и расходимость числовых рядов. Признаки сходимости, признак Даламбера.
16. Понятие знакопеременного ряда. Абсолютная и условная сходимость рядов.
17. Понятие функционального ряда, степенного ряда. Разложение элементарных функций в ряд Маклорена.
18. Элементы и множества, задания множеств. Операции над множествами.
19. Понятия события и вероятности события. Классическое определение вероятности.
20. Понятие случайной величины, закон ее распределения.
21. Математическое ожидание дискретной случайной величины, дисперсия случайной величины.
22. Матрицы. Определение и свойства матриц.
23. Определители. Определение и свойства определителей.
24. Общие понятия систем линейных алгебраических уравнений.
25. Матричный метод решения систем уравнений.
ЛИТЕРАТУРА
1. Богомолов Н. В. Практические занятия по математике. – М.,Высшая школа. 2014, - 495с.
2. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука, 1980.
3. Дадаян А.А. Математика: Учебник. - М.: ФОРУМ: ИНФРА-М, 2011. –
552с.- (Серия профессиональное образование)
3. Математика. Под редакцией Омельченко В.П., Курбатова Э.В. - Ростов-на-Дону «Феникс», 2014.-380 с. (среднее профессиональное образование)
4. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие – 5-е издание стер. – Ростов Н/Д: Феникс 2011. – с.47-158.
5. Федеральные государственные образовательные стандарты среднего
профессионального образования (ФГОС СПО).
Дата: 2019-02-19, просмотров: 309.