Относительная частота случайного события в серии экспериментов Бернулли.

Случайным событием называется такое событие, которое при осуществлении некоторых условий может произойти или не произойти.

Относительной частотой (или просто частотой) случайного события А, называется отношение числа появления данного события к общему числу проведенных одинаковых испытаний, в каждом из которых могло появиться или не появиться данное событие. Будем писать так:

Элементарные исходы, классическое определение вероятности.

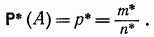Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равно­возможных исходов опыта, в котором может появиться это событие. Вероятность события А обозначают через Р (А). В соответствии с определением P(A)=m/n , где m - число элементарных исходов, благоприятствующих событию А; n - число всех равновозможных элементарных исходов опыта, образующих полную группу событий.

Сумма, произведения событий, противоположное событие.

1) Суммой событий А и В называется третье событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

2) Произведением событий А и В называется третье событие АВ, которое наступает тогда и только тогда, когда оба события: А и В.

3) Противоположными событиями называют два несовместных события, образующих полную группу. Обозначают противоположные события чертой сверху: событие Ā противоположно событию A.

Правило сложения вероятностей, аксиома счетной аддитивности вероятности, правило умножения вероятностей, независимость случайных событий.

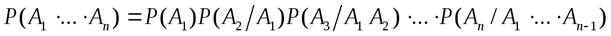Формула умножения: Пусть события А₁,…,А_n таковы, что 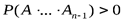. Тогда

Формула умножения вероятностей:

Независимость случайных событий: События A и В называются независимыми, если

Если равенство не выполняется, то события A и В будем называть зависимыми.

Правило сложения вероятностей: Если события А и В несоместны, то вероятность того, что осуществляется одно из этих событий, равна сумме их вероятностей. Р(А+В) = Р(А) – Р(В)

Следствие: Сумма вероятностей событий , образующих полную группу равна 1

Р(А₁) + Р(А₂)+….+Р(А_n) = 1

В частности : Р(А) +Р( 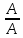) = 1

Аксиома счетной аддитивности вероятности:

Формула полной вероятности. Формула Байеса.

Формула полной вероятности: Если событие А может произойти только при выполнении одного из событий 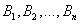, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле:

.

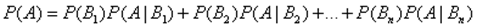
Какой вид имеют доверительные интервалы для математического ожидания нормальной случайной величины при известном среднеквадратическом отклонении, при неизвестном среднеквадратическом отклонении?

Относительная частота случайного события в серии экспериментов Бернулли.

Случайным событием называется такое событие, которое при осуществлении некоторых условий может произойти или не произойти.

Относительной частотой (или просто частотой) случайного события А, называется отношение числа появления данного события к общему числу проведенных одинаковых испытаний, в каждом из которых могло появиться или не появиться данное событие. Будем писать так: