Появление реляционной модели и вообще теории реляционных СУБД связывают с именем Э.Кодда, опубликовавшего в 1970 году статью с изложением принципов реляционного подхода к созданию и применению СУБД. В основе реляционной модели базы данных лежит математическое понятие отношения, откуда и происходит название этого типа модели БД.
Пусть 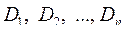 – некоторые множества, необязательно различные. Выражение
– некоторые множества, необязательно различные. Выражение 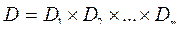 называется декартовым произведением названных множеств. Оно само является множеством и состоит из всех упорядоченных последовательностей или кортежей, вида
называется декартовым произведением названных множеств. Оно само является множеством и состоит из всех упорядоченных последовательностей или кортежей, вида 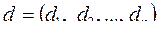 , где
, где 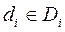 , i= 1, 2, …, n.
, i= 1, 2, …, n.
В декартовом произведении D каждое из множеств 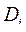 называется доменом. Домены могут быть различны по характеру и числу входящих в них элементов. Например, домен
называется доменом. Домены могут быть различны по характеру и числу входящих в них элементов. Например, домен 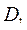 может представлять фамилии (с инициалами) студентов вуза;
может представлять фамилии (с инициалами) студентов вуза; 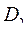 - годы обучения студента в вузе;
- годы обучения студента в вузе; 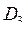 - названия факультетов и т.д.
- названия факультетов и т.д.
Подмножество 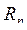 декартова произведения D (
декартова произведения D ( 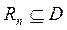 ) называется n–местным отношением. Число n называется степенью или арностью отношения. При n=1 отношение является унарным, при n=2 – бинарным, при n=3 – тернарным и т.д. Число всех различных кортежей
) называется n–местным отношением. Число n называется степенью или арностью отношения. При n=1 отношение является унарным, при n=2 – бинарным, при n=3 – тернарным и т.д. Число всех различных кортежей 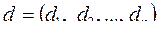 , образующих отношение
, образующих отношение 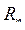 , называется кардинальным числом этого отношения.
, называется кардинальным числом этого отношения.
Отношение удобно представлять в виде таблицы. Строками такой таблицы являются кортежи, образующие отношение, а каждый из столбцов соответствует определенному домену. Для n–арного отношения i–й столбец соответствует домену 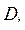 , где i=1,2,…,n. Число строк в таблице, представляющей отношение, равно кардинальному числу этого отношения. Поскольку по определению отношение является множеством, порядок следования кортежей в строках таблицы безразличен.
, где i=1,2,…,n. Число строк в таблице, представляющей отношение, равно кардинальному числу этого отношения. Поскольку по определению отношение является множеством, порядок следования кортежей в строках таблицы безразличен.
Если каждому из столбцов таблицы присвоить уникальное имя, то можно в произвольном порядке переставлять и столбцы таблицы. Разумеется, при перестановке столбцов необходимо менять местами и соответствующие этим столбцам элементы всех кортежей отношения.
Выраженное в табличной форме отношение совпадает с хорошо известным способом представления набора данных в виде последовательности записей с той же структурой. При этом каждый столбец таблицы-отношения соответствует определенному полю записи, а каждый кортеж – конкретной записи.
Однако не всякая таблица записей является отношением. Для того чтобы таблица была отношением, необходимо выполнение следующих условий:
- все записи в таблице должны иметь одну и ту же структуру;
- каждая запись в таблице должна быть уникальной;
- значения элементов одного и того же столбца таблицы должны принадлежать одному и тому же домену;
- имена столбцов должны быть различны.
В качестве имен столбцов в таблице, представляющей отношение, не всегда можно использовать имена, или обозначения, доменов, так как среди доменов, из которых образуется отношение, могут быть и совпадающие домены.
При рассмотрении реляционной модели БД в табличной форме вместо термина "столбец" обычно используют термин "атрибут". С использованием понятия атрибута отношение часто выражают в виде символьной строки R ( A 1, A 2,…, AM ), где R – название отношения; - A 1, A 2,…, AM - упорядоченная последовательность имен, или названий, атрибутов.
Как правило, один или несколько атрибутов в каждом отношении используются в качестве ключа. Ключ – такой атрибут (или совокупность нескольких атрибутов), значение которого идентифицирует каждый кортеж, или запись, в таблице, представляющей данное отношение. Ключ, состоящий из нескольких атрибутов, называется комбинированным. Комбинированный ключ должен быть неизбыточным, т.е. таким ключом, из которого нельзя удалить ни один из входящих в него атрибутов без того, чтобы ключ перестал однозначно идентифицировать записи в таблице.
Ключ данного отношения называется первичным ключом. В теории реляционных моделей СУБД используется также понятие "внешний ключ". Внешний ключ – такой атрибут (или комбинация атрибутов) данного отношения, который является первичным ключом для некоторого другого отношения.
В реляционной модели данных каждое отношение должно быть нормализовано. Говорят, что отношение нормализовано, если каждое значение любого атрибута в каждом кортеже отношения является неделимым, или атомарным элементом. Таким элементом может быть данное базового типа (целое или вещественное число, значение логического типа и т.д.) или символьная строка. Определенное таким образом понятие нормализованного отношения соответствует первой нормальной форме и обозначается 1NF. В теории реляционных моделей СУБД изучаются также вторая, третья, четвертая нормальные формы отношений, которые отличаются от формы 1NF различным характером функциональной зависимости атрибутов друг от друга и от первичного ключа.
С точки зрения пользователя реляционная модель базы данных представляется в виде совокупности поименованных нормализованных отношений, различающихся степенями и кардинальными числами. Для более глубокого уяснения сущности реляционной модели БД отношению можно поставить в соответствие традиционный файл с однотипными записями, кортежу отношения – экземпляр записи файла, а атрибуту – поименованное поле в структуре записи файла. Нормализованное отношение нередко называют также плоским файлом вследствие того, что каждое значение атрибута в любом кортеже отношения – неделимый элемент. Такое значение является либо числом, либо строкой символов.
Для манипулирования данными в реляционных СУБД создан целый ряд языков, которые называются также подъязыками данных. В зависимости от характера математического аппарата, лежащего в основе языков, все ЯМД в реляционных СУБД можно разделить на два главных класса: языки реляционной алгебры; языки реляционного исчисления.
Рассмотрим кратко сущности языков обоих классов. Языки реляционной алгебры основаны на реляционной алгебре (ее называют также реляционной алгеброй Кодда), характеризующейся определенным набором операций, которые можно выполнять над отношениями в реляционной СУБД. К таким операциям относятся традиционные операции над множествами (объединение, пересечение, разность, декартово произведение), а также специальные реляционные операции, важнейшими из которых являются операции проекции, соединения и выбора.
При выполнении операций объединения, пересечения и разности участвующие в них отношения должны удовлетворять свойству совместимости по объединению. Два отношения совместимы по объединению (или просто совместимы), если они имеют одну и ту же степень (т.е. одно и то же число атрибутов) и совпадающие атрибуты, причем значения атрибутов в каждой паре одинаковых атрибутов из обоих отношений должны быть элементами одного и того же домена. Операции объединения, пересечения, разности и декартового произведения в реляционных СУБД обозначают принятыми в математике символами È, Ç, /, ´.
Объединением двух совместимых отношений R 1, R 2 называется отношение R, состоящее из всех кортежей, принадлежащих хотя бы одному из отношений R 1, R 2. Пусть, например,
 ,
,
где 
Тогда 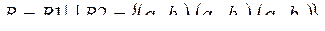
Пересечением двух совместимых отношений R 1, R 2 называется отношение R, которое состоит из всех кортежей, являющихся общими для отношений R 1, R 2. Для отношений R 1( A , B ) и R 2( A , B ) из предыдущего примера результат пересечения будет 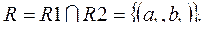
Разностью двух совместимых отношений R 1, R 2 называется отношение R, состоящее только из тех кортежей отношения R 1, которые отсутствуют в отношении R 2. Для примера отношений R 1( A , B ) и R 2( A , B ) их разность 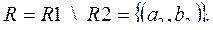
Декартовым произведением двух отношений R 1, R 2 (необязательно совместимых) называется отношение R, состоящее из всех таких картежей, каждый из которых есть конкатенация двух кортежей, по одному картежу из отношений R 1, R 2, причем на первом месте должен быть кортеж из R 1. Для отношений R 1( A , B ), R 2( A , B ) их декартово произведение
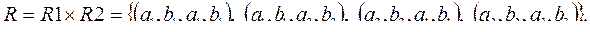
Операции объединения, пересечения и декартового произведения могут быть обобщены на произвольное число участвующих в них отношений.
Обратимся теперь к операциям проекции, соединения и выбора. Операция проекции является унарной и позволяет из заданного отношения R получить другое отношение R', в котором множество атрибутов является подмножеством атрибутов отношения R. Из одного и того же исходного отношения с помощью операции проекции можно получить несколько разных отношений. Для выполнения операции проекции необходимо задать исходное отношение, а также подмножество тех его атрибутов, которые должны составлять результирующее отношение. Таким образом, проекция исходного отношения осуществляется на заданные его атрибуты. Сокращенно связь между исходным отношением и отношением, являющимся результатом проекции, можно записать в виде R '=П R ( A ) ,где П – обозначение операции проекции; A – подмножество атрибутов исходного отношения R, на которое осуществляется проекция.
Отношение, являющееся результатом операции проекции, состоит из всех кортежей исходного отношения, в которых присутствуют значения атрибутов, входящих в множество А. При этом порядок следования атрибутов в результирующем отношении может отличаться от порядка следования этих же атрибутов в исходном отношении.
Следующая специальная операция реляционной алгебры – операция соединения – позволяет создать новое отношение из двух и более исходных отношений, имеющих хотя бы один общий атрибут. При этом для каждого из исходных отношений можно указать лишь те атрибуты, которые должны войти в результирующее отношение. Для того, чтобы результирующее отношение содержало хотя бы один кортеж, необходимо, чтобы по крайней мере в одном из кортежей каждого исходного отношения общий атрибут имел одно и то же значение.
Последняя из трех основных специальных операций реляционной алгебры – операция выбора – унарная и обеспечивает выбор некоторого подмножества картежей из исходного отношения. В результате операции получается новое отношение, состоящее из таких кортежей исходного отношения, в которых значение одного (или нескольких) атрибута удовлетворяет заданному в операции условию.
Вторая большая группа ЯМД в реляционных СУБД использует реляционное исчисление, основанное на классическом исчислении предикатов и представляющее собой набор правил для записи выражений, которые обеспечивают формирование новых отношений в терминах заданных существующих отношений. При записи таких выражений применяются операторы сравнения =, ¹, <, £, >, ³, логические операторы Ù, Ú,Ø и кванторы $,".
Различие между двумя описанными классами языков реляционных моделей СУБД проявляется главным образом в том, как пользователь может выражать свои запросы к СУБД. Применяя язык реляционной алгебры, пользователь должен записать в соответствующем порядке всю последовательность операций, которые необходимо выполнить для получения желаемого результата. Это, конечно, требует от пользователя больших усилий. В то же время на языке реляционного исчисления пользователь записывает свой запрос лишь в виде декларации желаемого результата, а СУБД автоматически "развернет" эту декларацию в правильную последовательность необходимых действий. Таким образом, различие между языками реляционной алгебры и реляционного исчисления такое же, как и между двумя известными в математике способами определения множества. Один из этих двух способов обеспечивает построение желаемого множества путем выполнения ряда теоретико-множественных операций над некоторыми заданными исходными множествами, а другой способ – путем указания определяющего свойства желаемого множества.
Теория и практика применения СУБД представляет собой в настоящее время стремительно развивающуюся область вычислительной техники, в которой заняты тысячи ученых, инженеров и просто пользователей.
ЗАДАЧИ И УПРАЖНЕНИЯ
В настоящем разделе содержатся задачи и упражнения по структурам данных. Эти задачи и упражнения расположены в восьми подразделах, посвященных определенному типу структур данных.
Векторы
1. Даны натуральные числа n, a1, ..., an. Определить количество членов ak последовательности a1, ..., an:
| а) являющихся нечетными числами; |
| б) являющихся квадратами четных чисел; |
| в) кратных 3 и не кратных 5; |
г) удовлетворяющих условию 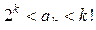 ; ;
|
д) удовлетворяющих условию 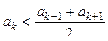 ; ;
|
| е) имеющих четные порядковые номера и являющихся нечетными числами. |
2. Даны натуральные числа n, q1, ..., qn. Найти те члены q i последовательности q1, ..., q n , которые
а) являются удвоенными нечетным числами;
б) при делении на 7 дают остаток 1, 2 или 5;
в) обладают тем свойством, что корни уравнения 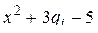 действительны и положительны.
действительны и положительны.
3. Дано натуральное число n. Получить сумму тех чисел вида 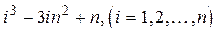 , которые являются утроенными нечетными.
, которые являются утроенными нечетными.
4. Даны целые числа a1, ..., a50. Получить сумму тех чисел данной последовательности, которые
| а) кратны 5; |
| б) нечетны и отрицательны; |
в) удовлетворяют условию 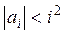 . .
|
5. Даны натуральное число n, целые числа a1, ..., a n . Найти количество и сумму тех членов данной последовательности, которые делятся на 5 и не делятся на 7.
6. Даны натуральные числа n, p, целые числа a1, ..., an. Получить произведение членов последовательности a1, ..., an, кратных p.
7. Даны целые числа p, q, a1, ..., a67 ( 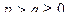 ).В последовательности a1, ..., a67 заменить нулями члены, модуль которых при делении на p дает в остатке q.
).В последовательности a1, ..., a67 заменить нулями члены, модуль которых при делении на p дает в остатке q.
8. Даны натуральное число n, действительные числа a1, ..., an. Получить удвоенную сумму всех положительных членов последовательности a1, ..., an.
9. Даны натуральное число n, действительные числа a1, ...,an. Вычислить обратную величину произведения тех членов ai последовательности a1, ..., an, для которых выполнено i+1 <ai <i!.
10. Даны натуральное число n, действительные числа a1, ...,an. В последовательности а1, ..., an все отрицательные члены увеличить на 0.5, а все не отрицательные заменить на 0.1.
11. Даны натуральное число n, действительные числа x1, ..., x n. В последовательности x1, ..., x n все члены, меньшие двух, заменить нулями. Кроме того, получить сумму членов, принадлежащих отрезку [3,7], а также число таких членов.
12. Даны натуральное число n, действительные числа a1, ..., an. В последовательности a1, ..., an все неотрицательные члены, не принадлежащие отрезку [1, 2], заменить на единицу. Кроме того, получить число отрицательных членов и число членов, принадлежащих отрезку [1, 2].
13. Даны натуральное число n, целые числа a1, ..., an. Получить сумму положительных и число отрицательных членов последовательности a1, ..., a n .
14. Даны натуральное число n, целые числа a1, ..., an. Заменить все большие семи члены последовательности a1, ..., an числом 7. Вычислить количество таких членов.
15. Даны целые числа 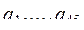 . Получить число отрицательных членов последовательности
. Получить число отрицательных членов последовательности 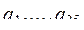 и число нулевых членов всей последовательности
и число нулевых членов всей последовательности 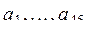 .
.
16. Пусть 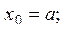
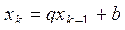
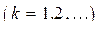 . Даны: неотрицательное целое n, действительные a, b, c, d, q
. Даны: неотрицательное целое n, действительные a, b, c, d, q 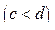 . Принадлежит ли
. Принадлежит ли 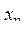 интервалу
интервалу 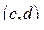 ?
?
17. Даны: натуральное число n, целые числа a, 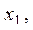 ...,
..., 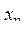 . Если в последовательности
. Если в последовательности 
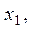 ...,
..., 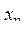 есть хотя бы один член, равный a, то получить сумму всех членов, следующих за первым таким членом; в противном случае ответом должно быть число 10.
есть хотя бы один член, равный a, то получить сумму всех членов, следующих за первым таким членом; в противном случае ответом должно быть число 10.
18. Даны: натуральное число n, действительные числа a, b, 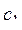 , ...,
, ..., 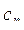 . Верно ли, что при
. Верно ли, что при 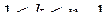 всякий раз, когда
всякий раз, когда 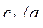 , выполнено
, выполнено 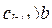 ?
?
19. Даны целые числа 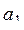 , ...,
, ..., 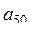 . Получить последовательность
. Получить последовательность 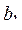 , ...,
, ..., 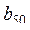 , которая отличается от исходной тем, что все нечетные члены удвоены.
, которая отличается от исходной тем, что все нечетные члены удвоены.
20. Вычислить 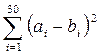 , где
, где
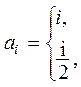
| если i нечетное, в противном случае; | 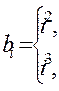
| если i нечетное, в противном случае. |
21. Даны натуральные числа n, 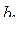 ,...,
,..., 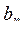 . Вычислить
. Вычислить 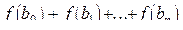 , где
, где
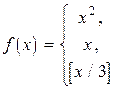
| если x кратно 3 , если x при делении на 3 дает остаток 1 в остальных случаях |
22. Даны натуральное число n, действительные числа r , 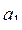 ,...,
,..., 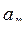
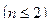 . Сколько среди точек (
. Сколько среди точек ( 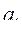 ,
, 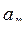 ), ..., (
), ..., ( 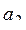 ,
, 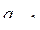 ), (
), ( 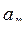 ,
, 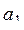 ) таких которые принадлежат кругу радиуса r с центром в начале координат?
) таких которые принадлежат кругу радиуса r с центром в начале координат?
23. Даны целые числа а, n, 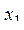 , ...,
, ..., 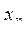 (n>0). Определить, каким по счету идет в последовательности
(n>0). Определить, каким по счету идет в последовательности 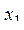 , ...,
, ..., 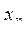 член, равный а. Если такого члена нет, то ответом должно быть число 0.
член, равный а. Если такого члена нет, то ответом должно быть число 0.
24. Даны натуральное число n, действительные числа 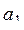 , ...,
, ..., 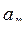 . Получить:
. Получить:
а) 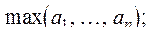
| б) 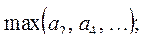
|
в) 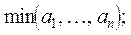
| г) 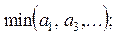
|
д) 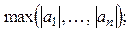
| е) 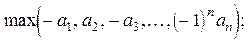
|
ж) 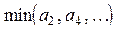 + + 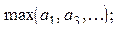
| з) 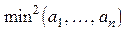 - - 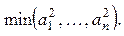
|
25. Даны натуральное число n, действительные числа 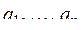 .
.
a) Верно ли, что отрицательных членов в последовательности 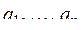 больше чем положительных ?
больше чем положительных ?
б) Верно ли, что наибольший член последовательности 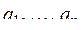 по модулю больше единицы ?
по модулю больше единицы ?
26. У прилавка в магазине выстроилась очередь из n покупателей. Время обслуживания продавцом i-го покупателя равно  (i=1, ... , n). Пусть даны натуральное число n и действительные
(i=1, ... , n). Пусть даны натуральное число n и действительные  . Получить
. Получить  , где ci - время пребывания i - го покупателя в очереди (i=1, ... , n). Указать номер покупателя, для обслуживания которого продавцу потребовалось самое малое время.
, где ci - время пребывания i - го покупателя в очереди (i=1, ... , n). Указать номер покупателя, для обслуживания которого продавцу потребовалось самое малое время.
27. В некоторых видах спортивных состязаний выступление каждого спортсмена независимо оценивается несколькими судьями, затем из всей совокупности оценок удаляются наиболее высокая и наиболее низкая, а для оставшихся оценок вычисляется среднее арифметическое, которое и идет в зачет спортсмену. Если наиболее высокую оценку выставило несколько судей, то из совокупности оценок удаляется только одна такая оценка; аналогично поступают с наиболее низкими оценками.
Даны натуральное число n, действительные положительные числа  (n
(n 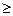 3). Считая, что числа
3). Считая, что числа 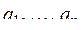 - это оценки, выставленные судьями одному из участников соревнований, определить оценку, которая пойдет в зачет этому спортсмену.
- это оценки, выставленные судьями одному из участников соревнований, определить оценку, которая пойдет в зачет этому спортсмену.
28. Даны натуральное число n, действительные числа  . Получить
. Получить 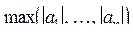 и
и 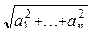 .
.
29. Дано натуральное число n. Найти наибольшее среди чисел 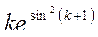 (k=1, ..., n), а также сумму всех этих чисел.
(k=1, ..., n), а также сумму всех этих чисел.
30. Даны натуральное число n, целые числа  . Найти:
. Найти:
а) наименьшее из четных чисел, входящих в последовательность a1-1, a 1 , ..., an;
б) наибольшее из нечетных и количество четных чисел, входящих в последовательность a 1 , ..., an , an+1.
31. Даны натуральное число n, действительные числа 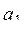 , ...,
, ..., 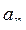 . Получить все натуральные числа j
. Получить все натуральные числа j 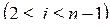 , для которых
, для которых 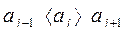 .
.
32. Пусть 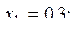
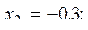
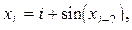 i=3, 4, ... . Среди
i=3, 4, ... . Среди 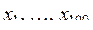 найти ближайшее к какому-нибудь целому.
найти ближайшее к какому-нибудь целому.
33. Пусть 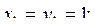
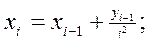
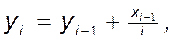 i=2, 3, ... . Получить
i=2, 3, ... . Получить 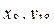 .
.
34. Пусть 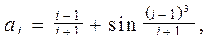 i=1, 2, ... . Дано натуральное n. Среди
i=1, 2, ... . Дано натуральное n. Среди  найти все положительные числа, среди положительных
найти все положительные числа, среди положительных  выбрать наименьшее число.
выбрать наименьшее число.
35. Пусть 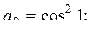
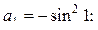
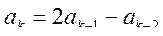 ; k= 2, 3, ... . Найти сумму квадратов тех чисел
; k= 2, 3, ... . Найти сумму квадратов тех чисел 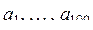 , которые не превосходят двух.
, которые не превосходят двух.
36. Даны натуральное число n, действительные числа  . В последовательности
. В последовательности  определить число соседств:
определить число соседств:
| а) двух положительных чисел; |
| б) двух чисел разного знака; |
| в) двух чисел одного знака, причем модуль первого числа должен быть больше модуля второго числа. |
37. Даны целые числа 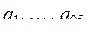 . Имеются ли в последовательности
. Имеются ли в последовательности 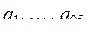 :
:
| а) два идущих подряд нулевых члена; |
| б) три идущих подряд нулевых члена? |
38. Даны натуральное число n, действительные числа 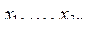 . Последовательность чисел
. Последовательность чисел 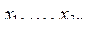 определяет на плоскости n квадратов со сторонами, параллельными координатным осям: так
определяет на плоскости n квадратов со сторонами, параллельными координатным осям: так 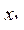 ,
, 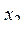 - координаты центра первого квадрата,
- координаты центра первого квадрата, 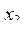 - длина его стороны; аналогично числа
- длина его стороны; аналогично числа 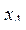 ,
, 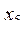 ,
, 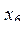 определяют второй квадрат,
определяют второй квадрат, 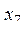 ,
, 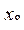 ,
, 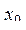 - третий и т.д. Имеются ли точки, принадлежащие всем квадратам? Если да, то указать координаты одной из них.
- третий и т.д. Имеются ли точки, принадлежащие всем квадратам? Если да, то указать координаты одной из них.
39. Даны натуральное число n, действительные числа 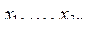 . Вычислить сумму чисел
. Вычислить сумму чисел 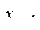 ,...,
,..., 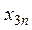 , которые превосходят по величине все числа
, которые превосходят по величине все числа 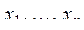 .
.
40. Даны действительные числа a, b (a<b), натуральное число n, функция y=f(x), определенная на отрезке [a, b]. Для значений аргумента 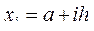 (i = 0, 1, ..., n),
(i = 0, 1, ..., n), 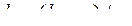 вычислить значения функции
вычислить значения функции 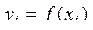
(i=0, 1,..., n). Вывести 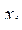 и
и 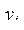 (i=0, 1, ..., n) в виде таблицы из двух колонок. В i-ю строку таблицы заносятся соответствующие значения
(i=0, 1, ..., n) в виде таблицы из двух колонок. В i-ю строку таблицы заносятся соответствующие значения 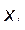 и
и 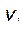 . Рассмотреть следующие функции:
. Рассмотреть следующие функции:
а)  , , 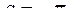 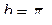 n=50; n=50;
|
б) 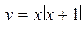 , a=-1, b=2, n=30; , a=-1, b=2, n=30;
|
в) 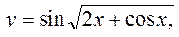 a=0, b=2 a=0, b=2 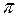 , n=50; , n=50;
|
г) 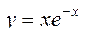 , a=-1, b=3, n=40; , a=-1, b=3, n=40;
|
д) 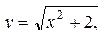 a=-3, b=5, n=40. a=-3, b=5, n=40.
|
41. Рассматривается последовательность 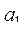 , ...,
, ..., 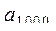 . Требуется определить, сколько членов последовательности с номерами 1, 2, 4, 8, 16, ... имеют значение, меньшее, чем 0.25. При этом считать, что
. Требуется определить, сколько членов последовательности с номерами 1, 2, 4, 8, 16, ... имеют значение, меньшее, чем 0.25. При этом считать, что
а) 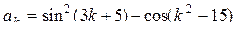 , k=1, 2, ..., 1000;
, k=1, 2, ..., 1000;
б) 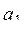 , ...,
, ..., 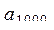 - заданные действительные числа;
- заданные действительные числа;
в) 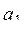 =0.01;
=0.01; 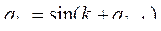 , k=2, ... , 1000.
, k=2, ... , 1000.
42. Даны натуральное число n, действительные числа 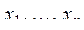 . Получить (1+r)/(1+s), где r - сумма всех тех членов последовательности
. Получить (1+r)/(1+s), где r - сумма всех тех членов последовательности 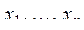 , которые не превосходят 1, а сумма s - сумма всех членов, больших 1.
, которые не превосходят 1, а сумма s - сумма всех членов, больших 1.
43. Даны натуральное число n, действительные числа 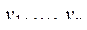 . Найти:
. Найти:
а) 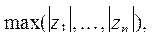 где где
| 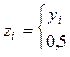
| при çyiç£2, в противном случае; |
б) 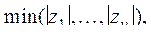 где где
| 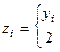
| при çyiç>1, в противном случае; |
в) 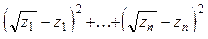 , где , где
| 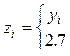
| при 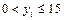 ,
в противном случае; ,
в противном случае;
|
г) 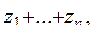 где где
| 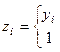
| при 0<çyiç<10, в противном случае; |
д) 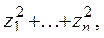 где где
| 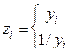
| при çyiç<1, в противном случае; |
44. Даны целые числа 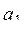 ,
, 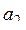 , ... Известно, что
, ... Известно, что 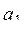 >0 и что среди
>0 и что среди 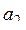 ,
, 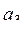 , ... есть хотя бы одно отрицательное число. Пусть
, ... есть хотя бы одно отрицательное число. Пусть 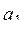 , ...,
, ..., 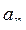 - члены данной последовательности, предшествующие первому отрицательному члену (n заранее не известно). Получить:
- члены данной последовательности, предшествующие первому отрицательному члену (n заранее не известно). Получить:
а) 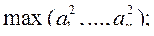
|
б) 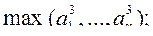
|
в) 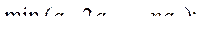
|
г) 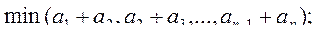
|
д) 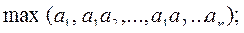
|
е) количество четных среди 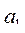 , ..., , ..., 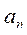 ; ;
|
и) количество квадратов нечетных чисел среди 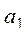 , ..., , ..., 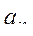 ; ;
|
ж) количество удвоенных нечетных среди 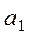 ,..., ,..., 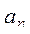 ; ;
|
з) количество полных квадратов среди 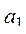 , ..., , ..., 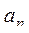 . .
|
45. Дано натуральное число n. Получить все натуральные делители.
46. Дано натуральное число n. Получить все такие натуральные q, что n делится на 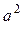 и не делится на
и не делится на 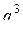 .
.
47. Даны натуральные числа m, n. Получить все их натуральные общие кратные, меньше mn.
48. Даны целые числа m, n (m 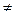 0, n
0, n 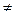 0). Получить все их общие делители (положительные и отрицательные).
0). Получить все их общие делители (положительные и отрицательные).
49. Даны натуральное числа n, действительные числа 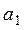 , ...,
, ..., 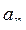 . Выяснить, является ли последовательность
. Выяснить, является ли последовательность 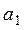 , ...,
, ..., 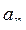 упорядоченной по убыванию.
упорядоченной по убыванию.
51. Даны натуральное число n, действительные числа 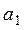 , ...,
, ..., 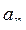 . Найти длину наименьшего отрезка числовой оси, содержащего числа
. Найти длину наименьшего отрезка числовой оси, содержащего числа 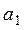 , ...,
, ..., 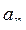 .
.
52. Даны действительные числа x, 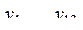 . Выяснить, во-первых, верно ли, что
. Выяснить, во-первых, верно ли, что 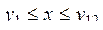 , и, во-вторых, верно ли, что
, и, во-вторых, верно ли, что 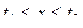 , где
, где 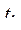 - наименьшее, а
- наименьшее, а 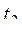 - наибольшее среди
- наибольшее среди 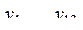 . (Какие комбинации ответов на первый и второй вопросы возможны?)
. (Какие комбинации ответов на первый и второй вопросы возможны?)
53. Даны натуральное число n, действительные числа а, 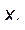 ,...,
,..., 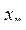 (
( 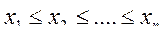 ). Получить последовательность
). Получить последовательность 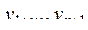 , членами которой являются члены последовательности
, членами которой являются члены последовательности 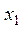 ,...,
,..., 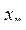 и значение а, такую, что
и значение а, такую, что 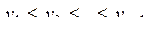 .
.
54. Даны натуральное число n, целые числа 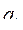 , ...,
, ..., 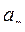 . Оставить без изменения последовательность
. Оставить без изменения последовательность 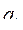 , ...,
, ..., 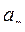 , если ее члены упорядочены по не убыванию или по не возрастанию. В противном случае получить подпоследовательность
, если ее члены упорядочены по не убыванию или по не возрастанию. В противном случае получить подпоследовательность 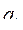 , ...,
, ..., 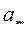 (m>n), где m таково, что либо
(m>n), где m таково, что либо 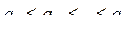 и
и 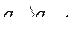 , либо
, либо 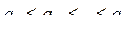 и
и 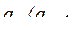 .
.
55. Даны натуральное число n, действительные числа а, 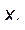 ,...,
,..., 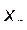 . Получить в порядке следования все
. Получить в порядке следования все 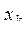 , удовлетворяющие неравенствам
, удовлетворяющие неравенствам 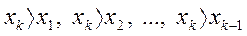 .
.
56. Даны натуральное число n, целые числа 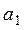 , ...,
, ..., 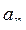 .
.
а) Выяснить, какое число встречается в последовательности 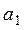 , ...,
, ..., 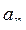 раньше - положительное или отрицательное. Если все члены последовательности равны нулю, то сообщить об этом.
раньше - положительное или отрицательное. Если все члены последовательности равны нулю, то сообщить об этом.
б) Найти номер первого четного члена последовательности 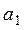 , ...,
, ..., 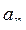 ; если четных членов нет, то ответом должно быть число 0.
; если четных членов нет, то ответом должно быть число 0.
в) Найти номер последнего нечетного члена последовательности 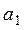 , ...,
, ..., 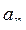 ; если нечетных членов нет, то ответом должно быть число n+1.
; если нечетных членов нет, то ответом должно быть число n+1.
57. Даны натуральное число n, целые числа 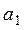 , ...,
, ..., 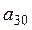 ,
, 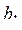 , ...,
, ..., 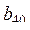 ,
, 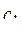 , ...,
, ..., 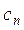 . Верно ли, что отрицательный член в последовательности
. Верно ли, что отрицательный член в последовательности 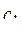 , ...,
, ..., 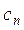 встречается раньше, чем в последовательностях
встречается раньше, чем в последовательностях 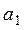 , ...,
, ..., 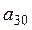 и
и 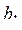 , ...,
, ..., 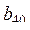 ? Предполагается, что каждая из последовательностей содержит хотя бы один отрицательный член.
? Предполагается, что каждая из последовательностей содержит хотя бы один отрицательный член.
58. Дано натуральное число n, действительные числа 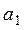 , ...,
, ..., 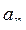 . Выяснить, образуют ли возрастающую последовательность числа:
. Выяснить, образуют ли возрастающую последовательность числа:
а) 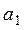 , ...,
, ..., 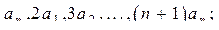
б) 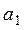 , ...,
, ..., 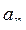 ,
, 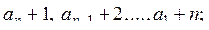
в) 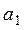 , ...,
, ..., 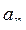 ,
, 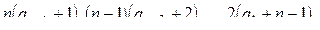
Матрицы
1. Даны целые числа а1, а2, а3. Получить целочисленную матрицу 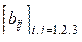 , для которой bij= ai-3aj.
, для которой bij= ai-3aj.
2. Даны действительные числа а1, ... , а10, b1, ... , b20. Получить действительную матрицу 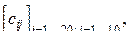 для которой
для которой 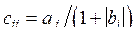 .
.
3. Получить целочисленную матрицу 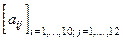 , для которой aij =i+2j.
, для которой aij =i+2j.
4. Дано натуральное число n. Получить действительную матрицу 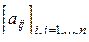 , для которой
, для которой
а) 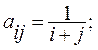 б)
б) 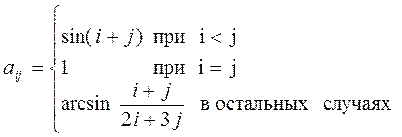
5. Дана действительная квадратная матрица 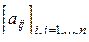 . Получить две квадратные матрицы
. Получить две квадратные матрицы 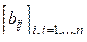 ,
, 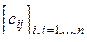 , для которых
, для которых
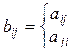
| при 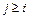 в оставшихся случаях
в оставшихся случаях
| 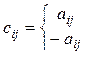
| при 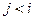 в оставшихся случаях
в оставшихся случаях
|
6. Получить действительную матрицу 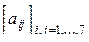 , первая строка которой задается формулой
, первая строка которой задается формулой 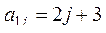 (
( 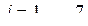 ), вторая строка задается формулой
), вторая строка задается формулой 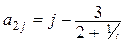 (j=1, ... ,7), а каждая следующая строка есть сумма двух предыдущих.
(j=1, ... ,7), а каждая следующая строка есть сумма двух предыдущих.
7. Дано натуральное число n, действительная матрица размера 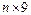 . Найти среднее арифметическое:
. Найти среднее арифметическое:
| а) каждого из столбцов; |
| б) каждого из столбцов, имеющих четные номера. |
8. Дано натуральное число n. Выяснить, сколько положительных элементов содержит матрица 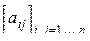 , если
, если
а) 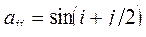 ; ;
| б) 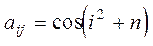 ; ;
| в) 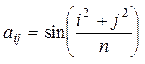 . .
|
9. Дана действительная квадратная матрица размера n ´ m, в которой не все элементы равны нулю. Получить новую матрицу путем деления всех элементов данной матрицы на ее наибольший по модулю элемент.
10. Даны натуральное число m, целые числа a1, ... , am и целочисленная квадратная матрица порядка m. Строку с номером i матрицы назовем отмеченной, если ai >0, и неотмеченной - в противном случае.
а) Нужно все элементы, расположенные в отмеченных строках матрицы, преобразовать по правилу: отрицательные элементы заменить на -1, положительные - на 1, а нулевые оставить без изменения.
б) Подсчитать число отрицательных элементов матрицы, расположенных в отмеченных строках.
11. Дана действительная квадратная матрица порядка 12. Заменить нулями все элементы, расположенные на главной диагонали и выше нее.
12. Даны действительные числа x1, ..., x8. Получить действительную квадратную матрицу порядка 8:
а) 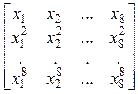 ; ;
| б) 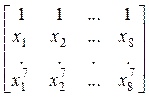
|
13. Дана действительная квадратная матрица размера n ´ m. Определить числа b1, ... ,bm , равные соответственно:
а) суммам элементов строк;
б) произведениям элементов строк;
в) наименьшим значениям элементов строк;
г) значениям средних арифметических элементов строк;
д) разностям наибольших и наименьших значений элементов строк.
14. Даны натуральное число n, действительная матрица 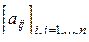 . Получить последовательность элементов главной диагонали a11, a22, ... , ann.
. Получить последовательность элементов главной диагонали a11, a22, ... , ann.
15. Все элементы с наибольшим значением в данной целочисленной квадратной матрице порядка 10 заменить нулями.
16. Дана действительная квадратная матрица размера 6´9. Найти среднее арифметическое наибольшего и наименьшего значений ее элементов.
17. Дана действительная квадратная матрица размера 18´ n. Найти значение наибольшего по модулю элемента с найденным значением модуля.
18. Дана действительная квадратная матрица размера n ´ m. Найти сумму наибольших значений элементов ее строк.
19. В данной действительной квадратной матрице порядка n найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный.
20. В данной действительной квадратной матрице размера 6´9 поменять местами строку, содержащую элемент с наибольшим значением, со строкой, содержащей элемент с наименьшим значением. Предполагается, что эти элементы единственны.
21. Даны натуральное число и квадратная матрица порядка n, действительные a1, ... , an+5 . Элементы последовательности домножить на 10, если наибольший элемент матрицы (в предположении, что такой элемент единственный) находятся на главной диагонали, и на 0.5 в противном случае.
22. В данной квадратной целочисленной матрице порядка 17 указать индексы всех элементов с наибольшим значением.
23. Дана действительная квадратная матрица размера n ´ m , все элементы которой различны. В каждой строке выбирается элемент с наименьшим значением, затем среди этих чисел выбирается наибольшее. Указать индексы элемента с найденным значением.
24. Дана действительная квадратная матрица размера n ´ m . Получить последовательность b1, ... , bn, где bk – это:
а) наибольшее из значений элементов k-й строки;
б) сумма из наибольшего и наименьшего из значений элементов k-й строки;
в) число отрицательных элементов k-й строки;
г) произведение квадратов тех элементов k-й строки, модули которых принадлежат отрезку [1, 1.5].
25. Даны натуральное число n, целочисленная матрица 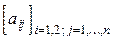 . Найти сумму тех из элементов a2j (j=1, ... , n ), для которых a1j имеет значение наибольшего среди значений a11, a12, ... , a1m.
. Найти сумму тех из элементов a2j (j=1, ... , n ), для которых a1j имеет значение наибольшего среди значений a11, a12, ... , a1m.
26. Дана целочисленная квадратная матрица порядка 8. Найти наименьшее из значений элементов столбца, который обладает наибольшей суммой модулей элементов. Если таких столбцов несколько, то взять первый из них.
27. Даны натуральное число n, целочисленная квадратная матрица порядка n. Получить b1, ... , bn, где bi – это:
а) наименьшее из значений элементов, находящихся в начале i-й строки матрицы до элемента, принадлежащего главной диагонали, включительно;
б) значение первого по порядку положительного элемента i-й строки (если таких элементов нет, то принять bi=1);
в) сумма элементов, расположенных за первым отрицательным элементом в i-й строке (если все элементы строки не отрицательны, то принять bi=1);
г) сумма элементов, предшествующих последнему отрицательному элементу i-й строки (если все элементы строки не отрицательны, то принять bi=1)
28. Дана целочисленная квадратная матрица порядка n. Найти номера строк:
а) все элементы которых - нули;
б) элементы каждой из которых одинаковы;
в) все элементы которых четны;
г) элементы каждой из которых образуют монотонную последовательность (монотонно убывающую или монотонно возрастающую);
д) элементы которых образуют симметрические последовательности (палиндромы).
29. Даны натуральное число n, действительное число x, действительная матрица размера n´2n. Получить последовательность b1, ... , bn из нулей и единиц, где bi =1, если элементы i-й строки матрицы не превосходит x, и bi =0 в противном случае.
30. Дана действительная квадратная матрица порядка n. Построить последовательность действительных чисел a1, ..., a n по правилу: если в i-й строке матрицы элемент, принадлежащий главной диагонали, отрицателен, то a i равно сумме элементов i-й строки, предшествующих первому отрицательному элементу; в противном случае a i равно сумме последних элементов i-й строки, начинающихся с первого по порядку неотрицательного элемента.
31. Дана действительная квадратная матрица порядка 10. В строках с отрицательным элементом на главной диагонали найти:
| а) сумму всех элементов; |
| б) наибольший из всех элементов. |
32. Дана действительная квадратная матрица порядка n. Рассмотрим те элементы, которые расположены в строках, начинающихся с отрицательного элемента. Найти сумму тех из них, которые расположены соответственно ниже, выше и на главной диагонали.
33. Дана действительная квадратная матрица порядка 9. Получить целочисленную квадратную матрицу того же порядка, в которой элемент равен единице, если соответствующий ему элемент исходной матрицы больше элемента, расположенного в его строке на главной диагонали, и равен нулю в противном случае.
34. Дана действительная квадратная матрица порядка n. Получить x1x2+ + 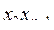 +...+ x n x 1 , где x k - наибольшее значение элементов k-й строки данной матрицы.
+...+ x n x 1 , где x k - наибольшее значение элементов k-й строки данной матрицы.
35. Даны действительная квадратная матрица порядка n, натуральные числа i, j (1£i£n, 1£j£n). Из матрицы удалить i-ю строку и j-й столбец.
36. Даны натуральное число  , действительная квадратная матрица порядка n . Построить последовательность b1, ..., b n из нулей и единиц, в которой b i = 1 тогда и только тогда, когда:
, действительная квадратная матрица порядка n . Построить последовательность b1, ..., b n из нулей и единиц, в которой b i = 1 тогда и только тогда, когда:
а) элементы i-й строки матрицы образуют возрастающую последовательность;
б) элементы i-й строки матрицы образуют возрастающую или убывающую последовательность.
37. Дана целочисленная квадратная матрица порядка 15. Выяснить, имеются ли в матрице ненулевые элементы, и если имеются, то указать индексы:
| а) одного из ненулевых элементов; |
| б) всех ненулевых элементов. |
38. Даны натуральные числа i, j, действительная матрица размера 18´24 (1£i<j£24). Поменять в матрице местами i-й и j-й столбцы.
39. Даны натуральное число n, действительная квадратная матрица порядка n . Построить последовательность b1, ..., b n из нулей и единиц, в которой b i=1 тогда и только тогда, когда в i-й строке матрицы есть хотя бы один отрицательный элемент.
40. С помощью 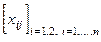 - действительной матрицы на плоскости задано n точек так, что x1j, x2j - координаты j-й точки. Точки попарно соединены отрезками. Найти длину наибольшего отрезка.
- действительной матрицы на плоскости задано n точек так, что x1j, x2j - координаты j-й точки. Точки попарно соединены отрезками. Найти длину наибольшего отрезка.
41. Даны натуральные числа n и m, действительное число r, действительная матрица размера n´m. Получить значение b1rn-1 +b2 rn-2 +...+bn, где bk - первый по порядку положительный элемент в k-й строке матрицы (k=1, ..., N); если в k-й строке нет положительных элементов, то bk= 0.5.
42. Найти сумму квадратов тех элементов a ij матрицы 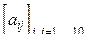 , для которых выполнено 2£i£9, 2£j£9,
, для которых выполнено 2£i£9, 2£j£9, 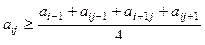 .
.
43. Дана действительная квадратная матрица порядка 9. Вычислить сумму тех из ее элементов, расположенных на главной диагонали и выше нее, которые превосходят по величине все элементы, расположенные ниже главной диагонали. Если на главной диагонали и выше нее нет элементов с указанным свойством, то ответом должно служить сообщение об этом.
44. Дана целочисленная матрица 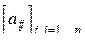 . Получить b1, ... ,bn, где bi- это
. Получить b1, ... ,bn, где bi- это
а) 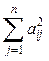 ; ;
| б) 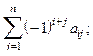
| в) 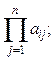
| г) 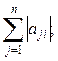
|
| д) | |||
| е) | |||
45. Будем называть соседями элемента с индексами i, j некоторой матрицы такие элементы этой матрицы, соответствующие индексы которых отличаются от i и j не более, чем на единицу. Для данной целочисленной матрицы 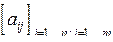 найти матрицу из нулей и единиц
найти матрицу из нулей и единиц 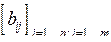 , элемент которой bij равен единице, когда:
, элемент которой bij равен единице, когда:
| а) все соседи aij меньше самого aij ; |
| б) все соседи aij и само aij равны нулю; |
| в) среди соседей aij есть не менее двух совпадающих с aij. |
46. Даны две целочисленные квадратные матрицы порядка 6. Найти последовательность из нулей и единиц b1..., b6 такую, что bi , когда:
а) все элементы i-й строки первой матрицы больше соответствующих элементов i-й строки второй матрицы;
б) все элементы i-х строк первой и второй матриц отрицательны;
в) i-е строки первой и второй матриц содержат вместе не более трех положительных элементов;
г) количество отрицательных и неотрицательных элементов i-й строки первой матрицы совпадает соответственно с количеством отрицательных и неотрицательных элементов i-й строки второй матрицы.
47. Таблица футбольного чемпионата задана квадратной матрицей порядка n, в которой все элементы, принадлежащие главной диагонали, равны нулю, а каждый элемент, не принадлежащий главной диагонали, равен 2,1 или 0 (числу очков, набранных в игре: 2 - выигрыш, 1 - ничья, 0 - проигрыш).
а) Найти число команд, имеющих больше побед, чем поражений.
б) Определить номера команд, прошедших чемпионат без поражений.
в) Выяснить, имеется ли хотя бы одна команда, выигравшая более половины игр.
48. Даны натуральные числа x1, y1, ..., xn, yn. Числа xi, yi рассматриваются как координаты i-й точки (i=1, ..., n). Обозначим через rij расстояние от i-й точки до j-й. Получить на экране заданные точки и соединить отрезком i-ю точку с j-й в том случае, если выполняется по крайней мере одно условие:
1) rij имеет наибольшее значение из ri1 ri2 , ..., rin ;
2) rij имеет наибольшее значение ri1 ri2 , ..., rin ;.
49. Дана целочисленная квадратная матрица порядка n. Каждый элемент матрицы ставится в соответствие точке, принадлежащей квадратной области экрана размером n´m точек. Левый верхний угол области имеет координаты (0, 0). Соответствие между элементами матрицы и точками области экрана устанавливается следующим образом: элемент матрицы, стоящий в строке с номером i и в столбце с номером j, соответствует точке экрана, находящейся на пересечении строки точек области с номером i и столбца точек области с номером j. Полагая, что каждый элемент матрицы задает цвет соответствующей точки экрана, получить на экране изображение, закодированное в матрице А.
50. Даны две целочисленные квадратные матрицы порядка n. В каждой из матриц закодировано изображение прямоугольной области экрана размером n´n точек с координатами левого верхнего угла (0, 0) (см. предыдущую задачу). В отличие от предыдущей задачи, все элементы обеих матриц - это числа, равные 0, если точка составляет фон, или 1, если точка - часть изображения. Получить на экране изображение, являющееся:
а) пересечением изображений, закодированных в первой и второй матрицах;
б) объединением изображений, закодированных в первой и второй матрицах.
51. Даны натуральные числа x1, y1, ..., xn, yn , целочисленная матрица 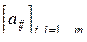 . Последовательность x1, y1, ... , xn, yn задает координаты n точек. Матрица указывает, как соединены между собой точки: aij = 1, если i-я точка соединена с j-й, и aij = 0 в противном случае (aij= aji). Получить на экране точки, заданные последовательностью x1, y1, ..., xn, yn, и соединить их между собой так, как указано в данной матрице.
. Последовательность x1, y1, ... , xn, yn задает координаты n точек. Матрица указывает, как соединены между собой точки: aij = 1, если i-я точка соединена с j-й, и aij = 0 в противном случае (aij= aji). Получить на экране точки, заданные последовательностью x1, y1, ..., xn, yn, и соединить их между собой так, как указано в данной матрице.
52. Пусть a1, a2, ... - последовательность квадратных матриц из нулей и единиц такая, что порядок матрицы ai равен 3i и
1) 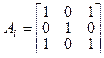
| 2) при i>1 имеет место  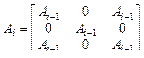 , ,
|
где 0 обозначает часть матрицы, заполненную нулями.
Дано натуральное число n. Построить изображение квадратной области экрана, закодированное в матрице An. Левый верхний угол области должен совпадать с левым верхним углом экрана. Опробовать различные способы использования цвета при построении изображения. Если фоновый цвет имеет номер 0, а остальные цвета - номера 1, ..., k, то при обработке элемента Aij не равного 0 можно, например, брать цвет с номером L+1, где L равно остатку от деления: i2+ j3 на k, и т.д.
53. Дана символьная квадратная матрица порядка 10. Заменить буквой a все ее элементы, расположенные выше главной диагонали.
54. Даны натуральное n, символьная квадратная матрица порядка n. Получить последовательность b1 , ..., bn из нулей и единиц, в которой bi= 1 тогда и только тогда, когда в i-й строке число символов * не меньше числа пробелов.
55. Дана символьная матрица размера 13´18. Найти:
а) номер первой по порядку строки, содержащий наибольшее число цифр;
б) номер первого по порядку столбца, содержащего наименьшее число пробелов на пересечении со строками, номера которых четны;
в) номер последней по порядку строки, содержащей наибольшее количество букв ш, щ;
г) номер последнего по порядку столбца, в котором содержится наибольшее количество попарно различных символов.
56. При перепечатке текста на пишущей машинке часто получается так, что в конце строки остается несколько неиспользованных позиций. Число неиспользованных позиций меняется от строки к строке, и поэтому правый край отпечатанного текста получается неровным. Типографский набор дает ровный правый край, в частности, за счет увеличения промежутков между словами, встречающимися в строке.
Предлагается задача выбора подходящих промежутков. Дана символьная матрица n´m, в каждой из строк которой имеется по крайней мере один пробел, за которым следует отличный от пробела символ (т.е. имеется по крайней мере одна группа пробелов внутри строки). За счет изменения групп пробелов внутри строк надо добиться того, чтобы в конце каждой из строк пробелы отсутствовали. Количества пробелов в разных группах, располагающихся внутри одной и той же строки, должны различаться не более чем на единицу.
57. Дана действительная квадратная матрица порядка n.
а) Найти сумму элементов первого столбца.
б) Найти сумму элементов главной и побочной диагоналей.
в) Найти наибольшее из значений элементов первой и последней строк.
г) Найти наименьшее из значений элементов побочной диагонали и двух соседних с ней линий.
д) Для данного натурального m ( 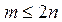 ) найти сумму тех элементов матрицы, сумма индексов которых равна m.
) найти сумму тех элементов матрицы, сумма индексов которых равна m.
е) Выяснить, верно ли, что наибольшее из значений элементов главной диагонали больше, чем наименьшее из значений элементов побочной диагонали.
Строки
1. Дана строка символов. Подсчитать, сколько раз среди символов строки встречается буква х.)
2. Дана строка символов; подсчитать:
а) сколько раз среди данных символов встречается символ + и сколько раз символ *;
б) общее число вхождений символов +, — , * в заданную строку.
3. Дана строка символов; преобразовать ее, заменив:
а) все восклицательные знаки точками ;
б) каждую точку многоточием (т. е. тремя точками);
в) каждую из групп стоящих рядом точек одной точкой;
г) каждую из групп стоящих рядом точек многоточием (т. е. тремя точками).
4. Дана строка символов  . Выяснить, имеются ли в последовательности
. Выяснить, имеются ли в последовательности  такие члены последовательности
такие члены последовательности 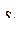 ,
, 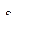 , что
, что 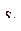 - это запятая, а
- это запятая, а 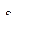 - тире.
- тире.
5. Дана строка символов  . Получить первое натуральное i , для которого каждый из символов
. Получить первое натуральное i , для которого каждый из символов 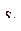 и
и 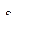 совпадает с буквой а. Если такой пары символов в последовательности
совпадает с буквой а. Если такой пары символов в последовательности  нет, то ответом должно быть число 0.
нет, то ответом должно быть число 0.
6. Дана строка символов  . Известно, что среди
. Известно, что среди  есть по крайней мере одна запятая. Найти такое натуральное i, что:
есть по крайней мере одна запятая. Найти такое натуральное i, что:
а) 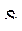 - первая по порядку запятая;
- первая по порядку запятая;
б) 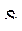 - последняя по порядку запятая.
- последняя по порядку запятая.
7. Дана строка символов  . Известно, что символ
. Известно, что символ 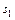 отличен от восклицательного знака и что среди
отличен от восклицательного знака и что среди 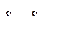 есть по крайней мере один восклицательный знак. Пусть
есть по крайней мере один восклицательный знак. Пусть  - символы данной последовательности, предшествующие первому восклицательному знаку ( n заранее неизвестно).
- символы данной последовательности, предшествующие первому восклицательному знаку ( n заранее неизвестно).
а) Определить количество пробелов среди  .
.
б) Выяснить, входит ли в последовательность  буква ю.
буква ю.
в) Выяснить, верно ли, что среди  имеются все буквы, входящие в слово шина.
имеются все буквы, входящие в слово шина.
г) Выяснить, имеется ли среди  пара соседствующих букв но или он.
пара соседствующих букв но или он.
д) Выяснить, имеется ли среди  пара соседствующих одинаковых символов.
пара соседствующих одинаковых символов.
е) Выяснить, верно ли, что существуют такие натуральные i и j, что 1<i<j<n и 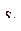 совпадает с
совпадает с 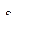 , а
, а 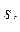 - с
- с 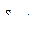 .
.
8. Дана строка символов. Удалить из данной последовательности все группы букв abcd.
9. Дана строка символов. Преобразовать ее, удалив каждый символ * и повторив каждый символ, отличный от *.
10. Дана строка символов, среди которых есть двоеточие.
а) Получить все символы, расположенные до первого двоеточия включительно.
б) Получить все символы, расположенные после первого двоеточия.
в) Получить все символы, расположенные между первым и вторым двоеточием. Если первого двоеточия нет, то получить все символы, расположенные после единственного имеющегося двоеточия.
11. Дана строка символов.
а) Подсчитать наибольшее количество идущих подряд пробелов.
б) Выяснить, верно ли, что в последовательности  имеется пять идущих подряд букв е.
имеется пять идущих подряд букв е.
12. Дана строка символов. Определить число вхождений в нее группы букв:
| а) abc; | б) aba. |
13. Дана строка символов. Заменить в ней каждую группу букв child группой букв children .
14. Дана строка символов. Исключить из нее группы символов, расположенные между скобками (, ). Сами скобки тоже должны быть исключены. Предполагается, что внутри каждой пары скобок нет других скобок.
15. Дана строка символов. Преобразовать ее следующим образом: если нет символа *, то оставить строку без изменения, иначе заменить каждый символ, встречающийся после первого вхождения символа *, на символ — .
16. Дана строка символов, среди которых есть хотя бы одна точка. Преобразовать ее, удалив все запятые, предшествующие первой точке, и заменив знаком + все цифры 3, встречающиеся после первой точки.
17. Дана строка символов  (n>1). Преобразовать последовательность
(n>1). Преобразовать последовательность  , заменив запятыми все двоеточия, встречающиеся среди
, заменив запятыми все двоеточия, встречающиеся среди 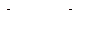 , и заменив точками все восклицательные знаки, встречающиеся среди
, и заменив точками все восклицательные знаки, встречающиеся среди  .
.
18. Дана строка символов  . Известно, что среди данных символов есть хотя бы один, отличный от пробела. Требуется преобразовать последовательность
. Известно, что среди данных символов есть хотя бы один, отличный от пробела. Требуется преобразовать последовательность  следующим образом. Удалить группы пробелов, которыми начинается и которыми заканчивается последовательность, а также заменить каждую внутреннюю группу пробелов одним пробелом. Если указанных групп нет в данной последовательности, то оставить последовательность без изменения.
следующим образом. Удалить группы пробелов, которыми начинается и которыми заканчивается последовательность, а также заменить каждую внутреннюю группу пробелов одним пробелом. Если указанных групп нет в данной последовательности, то оставить последовательность без изменения.
19. Дана строка символов. Группы символов, разделенные пробелами (одним или несколькими) и не содержащие пробелов внутри себя, будем называть словами.
а) Подсчитать количество слов в данной последовательности.
б) Подсчитать количество букв а в последнем слове данной последовательности.
в) Найти количество слов, начинающихся с буквы б.
г) Найти количество слов, у которых первый и последний символы совпадают между собой.
д) Найти какое-нибудь слово, начинающееся с буквы а.
е) Преобразовать данную последовательность, заменяя всякое вхождение слова это на то.
ж) Найти длину самого короткого слова.
20. Дана строка символов  Известно, что символ
Известно, что символ 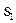 отличен от пробела и что среди
отличен от пробела и что среди  имеется хотя бы один пробел. Рассматриваются
имеется хотя бы один пробел. Рассматриваются  - символы, предшествующие первому пробелу (n заранее не известно). Преобразовать последовательность
- символы, предшествующие первому пробелу (n заранее не известно). Преобразовать последовательность  :
:
а) удалив из нее все символы, не являющиеся буквами;
б) заменив все малые буквы одноименными большими;
в) удалив все символы, не являющиеся буквами или цифрами, и заменив каждую большую букву одноименной малой;
г) удалив из каждой группы идущих подряд цифр, в которой более двух цифр и которой предшествует точка, все цифры, начиная с третьей (например, аb+0.1973-1.1 преобразуется в аb+0.19-1.1);
д) удалив из каждой группы цифр, которой не предшествует точка, все начальные нули (кроме последнего, если за ним идет точка).
21. Дана строка символов  . Оставить последовательность
. Оставить последовательность  без изменения, если в нее не входит символ *, иначе каждый символ /, предшествующий первому вхождению символа *:
без изменения, если в нее не входит символ *, иначе каждый символ /, предшествующий первому вхождению символа *:
| а) заменить на запятую | б) удалить из последовательности. |
22. Дана строка символов  . Если последовательность
. Если последовательность  является палиндромом, т.е. s1=sn, s2=sn-1 то оставить ее без изменения, иначе получить последовательность s1, s2, ..., sn-1, sn, sn-1, ..., s2, s1.
является палиндромом, т.е. s1=sn, s2=sn-1 то оставить ее без изменения, иначе получить последовательность s1, s2, ..., sn-1, sn, sn-1, ..., s2, s1.
23. Дана строка символов  . Если последовательность
. Если последовательность 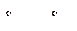 такова, что s1=s34, s2=s35, ... ,s33=s66, то оставить ее без изменения, иначе получить последовательность s1, s2, ..., s66, s1, s2, ..., s66 .
такова, что s1=s34, s2=s35, ... ,s33=s66, то оставить ее без изменения, иначе получить последовательность s1, s2, ..., s66, s1, s2, ..., s66 .
24. Дана строка символов  . Определить количество неверных равенств среди:
. Определить количество неверных равенств среди:
| а) s1=s41, s2=s42, ... , s40=s80; | б) s1=s80, s2=s79, ... , s40=s41. |
25. Дана строка символов. Будем рассматривать слова, образованные символами, входящими в последовательность s1, ... , sn , считая при этом, что количество символов в каждом слове не превосходит 15.
а) Найти какое-нибудь слово, оканчивающееся буквой д (если таких слов нет, то сообщить об этом).
б) Найти какое-нибудь слово, начинающееся буквой а и оканчивающееся буквой я (если таких слов нет, то сообщить об этом).
в) Удалить из s1, ... , sn все слова с нечетными порядковыми номерами и перевернуть все слова с четными номерами. Например, если n=21 и данная последовательность символов представляет собой последовательность
во_что_бы_то_ни_стало,
то должна получиться последовательность
отч_от_олатс.
г) Удалить из s1, ... , sn все слова, в которых встречается не более двух различных букв.
д) Удалить из s1, ... , sn все слова, оканчивающиеся группой букв кая или кое.
Записи и таблицы
1. Прямая на плоскости задается уравнением 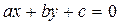 , где a и b одновременно не равны нулю. Будем рассматривать только прямые, для которых коэффициенты a, b, c - целые числа. Пусть f - таблица, содержащая коэффициенты нескольких прямых (не менее трех). Переписать из таблицы f в таблицу g коэффициенты тех прямых, которые:
, где a и b одновременно не равны нулю. Будем рассматривать только прямые, для которых коэффициенты a, b, c - целые числа. Пусть f - таблица, содержащая коэффициенты нескольких прямых (не менее трех). Переписать из таблицы f в таблицу g коэффициенты тех прямых, которые:
а) параллельны первой из прямых, заданной в таблице f;
б) указаны в а), но дополнительно требуется, чтобы все прямые были различны;
в) пересекают первую из прямых, заданных в таблице f;
г) указаны в в), но дополнительно требуется, чтобы среди прямых не было параллельных.
2. Условие предыдущей задачи сохраняется. Требуется получить в таблице g коэффициенты всех различных прямых таблицы f.
3. Багаж пассажира характеризуется количеством вещей и общим весом вещей. Дана таблица f, содержащая информацию о багаже нескольких пассажиров, информация о багаже каждого отдельного пассажира представляет собой соответствующую пару чисел.
а) Найти багаж, средний вес одной вещи в котором отличается не более чем на 0,3 кг от общего среднего веса вещи.
б) Найти число пассажиров, имеющих более двух вещей, и число пассажиров, количество вещей которых превосходит среднее число вещей.
в) Определить, имеется ли два пассажира, багажи которых совпадают по числу вещей и различаются по весу не более чем на 0,5 кг.
г) Выяснить, имеется ли пассажир, багаж которого превышает багаж каждого из остальных пассажиров и по числу вещей, и по весу.
д) Выяснить, имеется ли пассажир, багаж которого состоит из одной вещи весом не менее 30 кг.
е) Дать сведения о багаже, число вещей в котором не меньше, чем в любом другом багаже, а вес вещей не больше, чем в любом другом багаже с этим же числом вещей.
4. Сведения об ученике состоят из его имени и фамилии и названия класса (года обучения и буквы), в котором он учится. Дана таблица f, содержащая сведения об учениках школы.
а) Выяснить, имеются ли в школе однофамильцы.
б) Выяснить, имеются ли однофамильцы в каких-либо параллельных классах.
в) Выяснить, имеются ли однофамильцы в каком-нибудь классе.
г) Ответить на вопросы а)-в), но в отношении учеников, у которых совпадают и имя, и фамилия.
д) Выяснить, в каких классах насчитывается более 35 учащихся.
е) Выяснить, на сколько человек в восьмых классах больше, чем в десятых.
ж) Собрать в таблице g сведения об учениках 9 -х и 10-х классов, поместив вначале сведения об учениках класса 9а, затем 9б и т.д., затем 10а, 10б и т. д.
з) Получить список учеников данного класса по следующим образцам:
фамилия_имя
фамилия_и.
и.фамилия
5. Дана таблица f, содержащая те же самые сведения об учениках школы, что и в предыдущей задаче, и дополнительно отметки, полученные учениками в последней четверти.
а) Выяснить, сколько учеников школы не имеют отметок ниже четырех.
б) Собрать в файле g сведения о лучших учениках школы, т.е. об учениках, не имеющих отметок ниже четырех и по сумме баллов не уступающих другим ученикам своего и параллельных классов.
6. Сведения об автомобиле состоят из его марки, номера и фамилии владельца. Дана таблица f, содержащая сведения о нескольких автомобилях. Найти:
а) фамилии владельцев и номера автомобилей данной марки;
б) количество автомобилей каждой марки.
7. Дана таблица f, содержащая различные даты. Каждая дата - это число, месяц и год. Найти:
а) год с наименьшим номером;
б) все весенние даты;
в) самую позднюю дату.
8. Дана таблица f, содержащая сведения о книгах. Сведения о каждой из книг - это фамилия автора, название и год издания;
а) найти названия книг данного автора, изданных с 1960 года;
б) определить, имеется ли книга с названием “Информатика”. Если да, то сообщить фамилию автора и год издания. Если таких книг несколько, то сообщить имеющиеся сведения о всех этих книгах.
9. Дана таблицы f1, которая содержит номера телефонов сотрудников учреждения: указывается фамилия сотрудника, его инициалы и номер телефона. Найти телефон сотрудника по его фамилии и инициалам.
10. Дана таблицы f, содержащая сведения о кубиках: размер каждого кубика (длина ребра в сантиметрах), его цвет (красный, желтый, зеленый или синий) и материал (деревянный, металлический, картонный). Найти:
а) количество кубиков каждого из перечисленных цветов и их суммарный объем;
б) количество деревянных кубиков с ребром 3 см и количество металлических кубиков с ребром, большим 5 см.
11. Дана таблица f, содержащая сведения о веществах: указывается название вещества, его удельный вес и проводимость (проводник, полупроводник, изолятор).
а) найти удельные веса и названия всех полупроводников.
б) выбрать данные о проводниках и упорядочить их по убыванию удельных весов.
12. Дана таблица f, содержащая сведения об экспортируемых товарах: указывается наименование товара, сторона, импортирующая товар и объем поставляемой партии в штуках. Найти страны, в которые экспортируется данный товар, и общий объем экспорта.
13. Даны две таблицы f1 и f2. Таблица f1 - это инвентарная таблица, содержащая сведения о том, сколько изделий каких видов продукции хранится на складе (вид продукции задается его порядковым номером). Таблица f2 - это вспомогательная таблица, содержащая сведения о том, на сколько уменьшилось или увеличилось количество изделий по некоторым видам продукции. Вспомогательная таблица может содержать несколько сообщений по продукции одного вида или не содержать не одного такого сообщения. Обновить инвентарную таблицу на основе вспомогательной, образовав новую таблицу g.
14. Дана таблица f, содержащая сведения об игрушках: указывается название игрушки (например, кукла, кубики, мяч, конструктор и т.д.), ее стоимость в копейках и возрастные границы детей, для которых игрушка предназначена (например, для детей от двух до пяти лет). Получить следующие сведения:
а) названия игрушек, цена которых не превышает 4 руб. и которые подходят детям 5 лет;
б) цену самого дорогого конструктора, оформленную по образцу: ...руб. ...коп.;
в) названия более дорогих игрушек (цена которых отличается от цены самой дорогой игрушки не более чем на 1 руб.);
г) названия игрушек, которые подходят как детям 4 лет, так и детям 10 лет;
д) цены всех кубиков, оформленные по образцу, указанному в б);
е) можно ли подобрать игрушку, любую, кроме мяча, подходящую ребенку 3 лет, и дополнительно мяч так, чтобы суммарная стоимость не превосходила 5 руб.?;
ж) имеется ли мяч ценой 2 руб. 50 коп., предназначенный детям от 3 до 8 лет?; если нет, занести сведения об этой игрушке в файл f.
Списки
1. type ссылка = real;
вектор = array [ 1...100 ] of ссылка;
Считая, что все элементы вектора X отличны от nil, описать:
а) функцию max(x) для нахождения наибольшего из чисел, на которые ссылаются элементы вектора Х;
б) функцию negl(x), значением которой является первый из элементов вектора Х, ссылающихся на отрицательные числа, или nil, если таких элементов нет;
в) логическую функцию same(x), которая проверяет, есть ли в векторе Х хотя бы две одинаковые ссылки;
г) процедуру unique(x), которая в векторе Х все элементы, ссылающиеся на равные числа, заменяет на первый из этих элементов.
2. Одно из возможных представлений "длинного" текста - это разделить его на участки (строки) равной длины и создать массив ссылок на эти строки:
const d= ...;{длина строки}
n= ...;{максимальное число строк}
type строка = array [1..d] of char;
ссылка= строка;
текст =array [1..n] of ссылка;
(Если в тексте менее n строк, то последние элементы массива равны nill; в начале массива ссылок nill не должно быть. Если в операции над текстом указан номер отсутствующей строки, т.е. элемент массива с этим номером равен nill, то такая операция не выполняется.)
Используя данное представление текста, описать:
а) функцию числострок(Т) для подсчета числа строк в тексте Т;
б) логическую функцию элем(Т, i , j , c ), проверяющую, есть ли в тексте Т строка с номером i, и, если есть, присваивающую j-ю литеру этой строки параметру c;
в) процедуру перестановка(Т, i , j ), меняющую местами i-ю и j-ю строки текста Т;
г) процедуру замена(T, i , j ), заменяющую i-ю строку текста Т на копию j-й строки;
д) процедуру добавить(T, i , j ), добавляющую после i-й строки текста Т копию j-й строки;
е) процедуру удалить(T, i ), удаляющую i-ю строку из текста Т;
ж) логическую функцию поиск(Т, c , i , j ), определяющую, входит ли литера c в текст Т, и, если входит, присваивающую параметрам i и j "координаты" первого вхождения этой литеры: i - номер строки, а j - номер позиции в этой строке;
з) процедуру вывод(Т), печатающую построчно текст Т;
и) процедуру ввод(Т), считывающую из входного файла последовательность литер до первой точки и формирующую из них текст Т (последнюю строку, если надо, дополнить пробелами).
3. Описать процедуру, которая вставляет:
а) в начала списка L новый элемент E;
б) в конец списка L новый элемент E;
в) новый элемент E после первого элемента непустого списка L;
г) в список L новый элемент Е1 за каждым вхождением элемента Е;
д) в список L новый элемент Е1 перед первым вхождением элемента Е, если Е входит в L;
e) в непустой список L пару новых элементов Е1 и Е2 перед его последним элементом;
ж) в непустой список L, элементы которого упорядочены по неубыванию новый элемент Е так, чтобы сохранилась упорядоченность (ТЭ=real).
4. Описать процедуру, которая удаляет:
а) из непустого списка L первый элемент;
б) из списка L второй элемент, если такой элемент есть;
в) из списка L за каждым вхождением элемента Е один элемент, если такой есть и отличен от Е;
г) из непустого списка L последний элемент;
д) из списка L первый отрицательный элемент, если такой есть (ТЭ=integer);
e) из списка L все отрицательные элементы (ТЭ=real).
5. Программа. Заданный во входном файле текст (за ним следует точка) распечатать в обратном порядке.
6. Программа. Дана непустая последовательность натуральных чисел, за которыми следует 0. Напечатать порядковые номера тех чисел последовательности, которые имеют наибольшую величину.
7. Программа. Дано целое N>0, за которым следует N вещественных чисел. Напечатать эти числа в порядке их не убывания.
8. Описать процедуру или функцию, которая:
а) проверяет на равенство списки L1 и L2:
б) определяет, входит ли список L1 в список L2;
в) проверяет, есть ли в списке L хотя бы два одинаковых элемента;
г) переносит в конец непустого списка L его первый элемент;
д) переносит в начало непустого списка L его последний элемент;
е) добавляет в конец списка L1 все элементы списка L2;
ж) вставляет в список L за первым вхождением элемента Е все элементы списка L1, если Е входит в L;
з) переворачивает список L, т.е. изменяет ссылки в этом списке так, чтобы его элементы оказались расположенными в обратном порядке;
и) в списке L из каждой группы подряд идущих равных элементов оставляет только один;
к) оставляет в списке L только первые вхождения одинаковых элементов.
9. Описать рекурсивную функцию или процедуру, которая:
а) определяет, входит ли элемент Е в список L;
б) подсчитывает число вхождений элемента Е в список L;
в) находит максимальный элемент непустого списка L (ТЭ=real);
г) печатает в обратном порядке элементы списка L (ТЭ=char);
д) заменяет в списке L все вхождения Е1 на Е2;
е) удаляет из списка L первое вхождение элемента Е, если такое есть;
ж) удаляет из списка L все вхождения элемента Е;
з) строит L1 - копию списка L;
и) удваивает каждое вхождение элемента Е в список L;
к) находит среднее арифметическое всех элементов непустого списка L (ТЭ=real).
10. Описать процедуру, которая формирует список L, включив в него по одному разу элементы, которые:
а) входят хотя бы в один из списков L1 и L2;
б) входят одновременно в оба списка L1 и L2;
в) входят в список L1, но не входят в список L2;
г) входят в один из списков L1 и L2, но в то же время не входят в другой из них.
11. Описать процедуру, которая объединяет два упорядоченных по неубыванию списка L1 и L2 (TЭ=real) в один упорядоченный по неубыванию список:
а) построив новый список L;
б) меняя соответствующим образом ссылки в L1 и L2 и присвоив полученный список параметру L1.
12. Описать процедуру подстановка(L,L1,L2), которая в списке L заменяет первое вхождение списка L1 (если такое есть) на список L2.
13. type слово= цепочка;
цепочка=record буква: 'a'..'z';
связь: слово end;
ТЭ=слово;
Описать функцию или процедуру, которая:
а) в списке L переставляет местами первое и последнее непустые слова, если в L есть хотя бы два непустых слова;
б) печатает текст из первых букв всех непустых слов списка L;
в) удаляет мз непустых слов списка L их первые буквы;
г) печатает все непустые слова списка L;
д) определяет количество слов в непустом списке L, отличных от последнего.
14. Многочлен 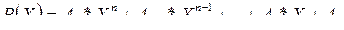
с целыми коэффициентами можно представить в виде списка, причем если A =0, то соответствующее звено не включается в список.
Описать тип данных, соответствующий такому представлению многочленов, и определить следующие функции и процедуры для работы с этими списками-многочленами:
а) логическую функцию равно(P,Q), проверяющую на равенство многочлены P и Q;
б) функцию знач(P,X), вычисляющую значение многочлена P в целочисленной точке X;
в) процедуру диф(P,Q), которая строит многочлен P - производную многочлена Q;
г) процедуру слож(P,Q,R), которая строит многочлен P - сумму многочленов Q и R;
д) процедуру вывод(P,V), которая печатает многочлен P как многочлен от переменной, однобуквенное имя которой является значением литерного параметра V; например, для многочлена 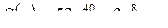 процедура
процедура
вывод(S',Y') должна напечатать 52*Y 40-3*Y 8+Y;
е) процедуру ввод(Р), которая считывает из входного файла безошибочную запись многочлена (за ней - пробел) и формирует соответствующий список-многочлен P.
15. Предложить и описать представление файлов (из элементов некоторого типа ТЭ) в виде списков и определить функцию eof 1(F) и процедуры reset 1(F), read 1(F,X), rewrite 1(F), write 1(F,X), реализующие при таком представлении файлов действия соответствующих стандартных функций и процедур.
16. Назовем (иерархическим) "списком" заключенную в круглые скобки последовательность элементов, разделенных запятыми; элементы списка - это атомы или снова списки:
<список>::=( ) ï (<элементы>)
<элементы>::=<элемент> ï <элемент>,<элементы>
<элемент>::=<атом> ï <список>
Под "атомом" понимается последовательность, содержащая от 1 до N букв и цифр, где N - заранее известное натуральное число. Пример подобного списка: (AD75,(3,(),(7H))).
Предложить и описать представление таких списков и определить следующие рекурсивные функции и процедуры для работы с ними:
а) логическую функцию member (A,L), проверяющую, входит ли атом А в список L;
б) логическую функцию equal (L1,L2), проверяющую на равенство списки L1 и L2;
в) процедуру printat (L), печатающую все атомы, входящие в список L;
г) процедуру printlist (L), печатающую список L в том виде, как он определен указанными выше металингвистическими формулами;
д) процедуру readlist (L), которая считывает из входного файла записанный без ошибок список и строит L - соответствующее представление этого списка.
17. Пусть L обозначает кольцевой (циклический) двунаправленный список с заглавным звеном при следующем описании такого списка:
type ТЭ= ... ; {тип элементов списка}
список2= звено2;
звено2=record элем:ТЭ2;
пред,след:список2 end;
и пусть Е обозначает величину типа ТЭ2.
Описать функцию или процедуру, которая:
а) определяет, является ли список L пустым;
б) печатает в обратном порядке элементы непустого списка L, (ТЭ2=char);
в) подсчитывает количество элементов списка L, у которых равные "соседи";
г) определяет, есть ли в списке L хотя бы один элемент, который равен следующему за ним (по кругу) элементу;
д) в списке L переставляет в обратном порядке все элементы между первым и последним вхождениями элемента Е, если Е входит в L не менее двух раз;
е) удаляет из списка L первый отрицательный элемент, если такой есть;
ж) из списка L, содержащего не менее двух элементов, удаляет все элементы, у которых одинаковые "соседи" (первый и последний элементы считать "соседями");
з) добавляет в конец списка L новый элемент E;
и) в списке L удваивает каждое вхождение элемента Е;
к) строит список L по однонаправленному списку L1;
л) в конец непустого списка L добавляет все его элементы, располагая их в обратном порядке (например, по списку из элементов 1,2,3 требуется построить список из элементов 1,2,3,3,2,1).
18. ("Считалка".) N ребят располагаются по кругу. Начав отсчет от первого, удаляют каждого K - го, смыкая круг после каждого удаления. Определить порядок удаления ребят из круга.
Решение этой задачи описать в виде программы (ее исходные данные - натуральные числа N и К), которая должна напечатать номера ребят в том порядке, как они удаляются из круга.
19. Определить, симметричен ли заданный во входном файле текст (за ним следует точка).
20. Дана последовательность из не менее чем двух различных натуральных чисел, за которой следует 0. Напечатать в обратном порядке все числа между наибольшим и наименьшим числами этой последовательности.
21. Дана непустая последовательность непустых слов из букв: между соседними словами - запятая, за последним словом - точка.
Напечатать все слова максимальной длины.
22. Дана непустая последовательность слов, в каждом из которых от 1 до 12 строчных латинских букв; между словами - пробел, за последним словом - точка. Напечатать эти слова по алфавиту, указав для каждого из них число его вхождений в эту последовательность.
23. Дана непустая последовательность слов, в каждом из которых от 1 до N строчных латинских букв; между словами - пробел, за последним словом - точка, максимальная длина слов (т.е. значение N) заранее не известна. Напечатать эти слова по алфавиту, указав для каждого из них число его вхождений в эту последовательность.
24. Дана непустая последовательность слов, в каждом из которых от 1 до 8 строчных латинских букв; между словами - пробел, за последним словом - точка. Напечатать эти слова в следующем порядке: сначала по алфавиту все слова из одной буквы, затем - по алфавиту все двухбуквенные слова и т.д. (одинаковые слова печатать по одному разу).
25. Дана непустая последовательность слов, в каждом из которых от 1 до N строчных латинских букв; между словами - пробел, за последним словом - точка. Максимальная длина слов (т.е. значение N) заранее не известна. Напечатать эти слова в следующем порядке: сначала по алфавиту все слова из одной буквы, затем - по алфавиту все двухбуквенные слова и т.д. (одинаковые слова печатать по одному разу).
26. Дан текст, оканчивающийся точкой. Среди литер этого текста особую роль играет знак #, появление которого в тексте означает отмену предыдущей литеры текста; k знаков # подряд отменяют k предыдущих литер (если такие есть). Напечатать данный текст, исправленный с учетом такой роли знака # (например, текст Х#ЭЕ##HELO#LO должен быть напечатан в виде HELLO).
27. Дано произвольное натуральное число N. Напечатать все цифры десятичной записи числа N!.
28. Дана запись многочлена (от переменной X) произвольной степени с целыми коэффициентами, причем его одночлены могут быть и не упорядочены по степеням Х, а одночлены одной и той же степени могут повторяться. (Возможный пример:  +
+ 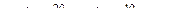 +
+ 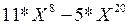 ). Требуется привести подобные члены в этом многочлене, после чего распечатать его по убыванию степеней X.
). Требуется привести подобные члены в этом многочлене, после чего распечатать его по убыванию степеней X.
29. Сформировать файл из натуральных чисел и напечатать порядковые номера тех элементов списка, построенного из элементов файла, за которыми стоит минимальный элемент.
30. Сформировать файл из символов, оканчивающихся точкой и выбросить из списка, построенного из элементов файла, круглые и квадратные скобки.
Очереди, стеки, деки
1. Для работы с очередью, т.е. последовательностью элементов, в которую элементы всегда добавляются в конец, а удаляются из начала ("первым пришел - первым ушел"), нужны обычно следующие операции:
ОЧИСТОЧ(Q) - создать пустую очередь Q (очистить очередь);
ПУСТОЧ(Q) - проверить, является ли очередь Q пустой;
ПЕЧОЧ(Q) – распечатать содержимое очереди;
ВОЧЕРЕДЬ(Q,x) - добавить в конец очереди Q элемент x;
ИЗОЧЕРЕДЬ(Q,x) - удалить из очереди Q первый элемент, присвоив его параметру x.
Требуется для каждого из указанных ниже представлений очереди описать соответствующий тип ОЧЕРЕДЬ, считая, что все элементы очереди имеют некоторый тип ТЭО, и реализовать в виде процедур или функций перечисленные операции над очередью ( если операция по тем или иным причинам не может быть выполнена, следует передать управление некоторой процедуре ОШИБКА(k), считая ее уже описанной, где k - номер ошибки: 1 - переполнение очереди, 2 - исчерпание очереди).
Представление очереди (n – целая константа >1):
а) для каждой очереди отводится свой массив из N компонентов типа ТЭО, в котором элементы очереди занимают группу соседних компонент, индексы первой и последней из которых запоминаются; при этом, когда очередь достигает правого края массива, все ее элементы сдвигаются к левому краю;
б) аналогичное представление, но массив как бы склеивается в кольцо, поэтому если очередь достигает правого края массива, то новые элементы записываются в начало массива;
в) для каждой очереди создается свой однонаправленный список из элементов типа ТЭО, при этом запоминаются ссылки на первое и последнее звенья списка.
2. Для работы со стеком, т.е. последовательностью элементов, в которой элементы всегда добавляются в конец и удаляются из конца ("последним пришел - первым ушел"), нужны обычно следующие операции:
ОЧИСТЕК(S) - создать пустой стек S (очистить стек);
ПЕЧСТЕК( S ) – распечатать содержимое стека;
ПУСТЕК(S) - проверить, является ли стек S пустым;
ВСТЕК(S,X) - добавить в конец стека S элемент X;
ИЗСТЕК(S,X) - удалить из очереди S последний элемент, присвоив его параметру X.
Требуется для каждого из указанных ниже представлений стека описать соответствующий тип СТЕК, считая, что все элементы стека имеют некоторый тип ТЭ C, и реализовать в виде процедур или функций перечисленные операции над стеком (если операция по тем или иным причинам невыполнима, следует передать управление некоторой процедуре ОШИБКА(k), считая ее уже описанной, где k - номер ошибки: 1 -переполнение стека, 2 -исчерпание стека).
Представление стека (n -целая константа>1):
а) для каждого стека отводится свой массив из n компонентов типа ТЭ C, в начале которого располагаются элементы стека, при этом запоминается индекс компоненты массива, занятой последним элементом стека;
б) для каждого стека создается свой однонаправленный список, в котором элементы стека располагаются в обратном порядке.
3. Используя очередь (предварительно выбрав и описав ее тип и создав все нужные для решения функции и процедуры для работы с этой очередью (ОЧИСТОЧ(Q), ПУСТОЧ(Q), ПЕЧОЧ(Q), ВОЧЕРЕДЬ(Q,x), ИЗОЧЕРЕДЬ(Q,x) (задача 1)), решить следующую задачу.
За один просмотр файла f и без использования дополнительных файлов напечатать элементы файла f в следующем порядке: сначала - все числа, меньшие A, затем - все числа из отрезка [A,B] (где A<B), и, наконец, - все остальные числа, сохраняя исходный взаимный порядок в каждой из этих трех групп чисел.
4. Используя очередь (предварительно выбрав и описав ее тип и создав все нужные для решения функции и процедуры для работы с этой очередью (ОЧИСТОЧ(Q), ПУСТОЧ(Q), ПЕЧОЧ(Q), ВОЧЕРЕДЬ(Q,x), ИЗОЧЕРЕДЬ(Q,x) (задача 1))), решить следующую задачу.
Содержимое текстового файла f, разделенное на строки, переписать в текстовый файл g, перенося при этом в конец каждой строки все входящие в нее цифры (с сохранением исходного взаимного порядка как среди цифр, так и среди остальных литер строки).
5. Используя очередь (предварительно выбрав и описав ее тип и создав все нужные для решения функции и процедуры для работы с этой очередью (ОЧИСТОЧ(Q), ПУСТОЧ(Q), ПЕЧОЧ(Q), ВОЧЕРЕДЬ(Q,x), ИЗОЧЕРЕДЬ(Q,x) (задача 1))), решить следующую задачу.
type имя= (Анна, ... , Яков);
дети = array [ имя , имя ] of boolen;
потомки =file of имя ;
Считая заданными имя И и массив Д типа ДЕТИ(Д[X,Y]=true, если человек по имени Y является ребенком человека по имени X), записать в файл P типа ПОТОМКИ имена всех потомков человека с именем И в следующем порядке: сначала - имена всех его детей, затем - всех его внуков, затем - всех правнуков и т.д..
6. Используя стек (предварительно выбрав и описав его тип и создав все нужные для решения функции и процедуры для работы с этим стеком (ПУСТЕК( S ), ПЕЧСТЕК( S ), ОЧИСТЕК( S ), ВСТЕК( S , x ) и ИЗТЕК( S , x ) (задача 2)), решить следующую задачу.
Напечатать содержимое текстового файла t, выписывая литеры каждой его строки в обратном порядке.
7. Используя стек (предварительно выбрав и описав его тип и создав все нужные для решения функции и процедуры для работы с этим стеком (ПУСТЕК( S ), ПЕЧСТЕК( S ), ОЧИСТЕК( S ), ВСТЕК( S , x ) и ИЗТЕК( S , x ) (задача 2))), решить следующую задачу.
Проверить, является ли содержимое текстового файла t правильной записью формулы следующего вида:
<формула>::= <терм> ï <терм>+<формула> ï <терм>-<формула>
<терм>::= <имя> ï <(<формула>) ï [<формула>] ï {<формула>}
<имя::= x ï y ï z
8. Используя стек (предварительно выбрав и описав его тип и создав все нужные для решения функции и процедуры для работы с этим стеком (ПУСТЕК( S ), ПЕЧСТЕК( S ), ОЧИСТЕК( S ), ВСТЕК( S , x ) и ИЗТЕК( S , x ) (задача 2)), решить следующую задачу.
В текстовом файле f записана без ошибок формула следующего вида:
<формула>::= <цифра>ïМ(<формула>,<формула>)ïм(<формула>,<формула>)
<цифра>::= 0 ï 1 ï 2 ï 3 ï 4 ï 5 ï 6 ï 7 ï 8 ï 9,
где М обозначает функцию max, а м обозначает функцию min.
Вычислить (как целое число) значение данной формулы (например,
М (5, м (6, 8)) ® 6).
9. Используя стек (предварительно выбрав и описав его тип и создав все нужные для решения функции и процедуры для работы с этим стеком (ПУСТЕК( S ), ПЕЧСТЕК( S ), ОЧИСТЕК( S ), ВСТЕК( S , x ) и ИЗТЕК( S , x ) (задача 2)), решить следующую задачу.
В текстовом файле LOG записано без ошибок логическое выражение (ЛВ) в следующей форме:
<ЛВ>::=true ï false ï (ù <ЛВ>) ï (<ЛВ> Ù <ЛВ> ï (<ЛВ> È <ЛВ>),
где знаки ù, Ù и È обозначают соответственно отрицание, коньюнкцию и дизьюнкцию.
Вычислить (как boolean) значение этого выражения.
10. Используя очередь и/или стек (предварительно выбрав и описав их типы и создав все нужные для решения функции и процедуры для работы над ними (задача 1 и/или 2)), решить следующую задачу.
В текстовом файле f записан текст, сбалансированный по круглым скобкам:
<текст>::=<пусто> ï <элемент><текст>
<элемент>::=<буква> ï (<текст>)
Требуется для каждой пары соответствующих открывающей и закрывающей скобок напечатать номера их позиций в тексте, упорядочив пары номеров в порядке возрастания номеров позиций закрывающих скобок. Например, для текста A+(45-f(X)*(B-C)) надо напечатать: 8 10; 12 16; 3 17.
11. Используя очередь и/или стек (предварительно выбрав и описав их типы и создав все нужные для решения функции и процедуры для работы над ними (задача 1 и/или 2)), решить следующую задачу.
В текстовом файле f записан текст, сбалансированный по круглым скобкам:
<текст>::=<пусто> ï <элемент><текст>
<элемент>::=<буква> ï (<текст>)
Требуется для каждой пары соответствующих открывающей и закрывающей скобок напечатать номера их позиций в тексте, упорядочив пары номеров в порядке возрастания номеров позиций открывающих скобок. Например, для текста A+(45-f(X)*(B-C)) надо напечатать 3 17; 8 10; 12 16.
12. Под "выражением" будем понимать конструкцию следующего вида:
<выражение>::=<терм> ï <терм><терм><знак><выражение>
<знак+->::=+ ï -
<терм>::=<множитель> ï <множитель>*<терм>
<множитель>::=<число>ï<переменная>ï(<выражение>)ï<множитель>**<число>
<число>::=<цифра>
<переменная>::=<буква>,
где ** обозначают возведение в степень.
Постфиксной формой записи выражения aÑb называется запись, в которой знак операции размещен за операндами: abÑ . Примеры:
a-b ® ab-
a*b+c ® ab*c- (т.е. (ab*)c+)
a*(b+c) ® abc+* (т.е. a(bc+)*)
a+b**c**d*e ® abc**d**e*+
Описать функцию value(postfix), которая вычисляет как целое число значение выражения (без переменных), записанного в постфиксной форме в текстовом файле postfix.
Использовать следующий алгоритм вычисления. Выражение просматривается слева направо. Если встречается операнд (число), то его значение (как целое) заносится в стек, а если встречается знак операции, то из стека извлекаются два последних элемента (это операнды данной операции), над ними выполняется операция и ее результат записывается в стек. В конце концов в стеке останется только одно число - значение всего выражения.
13. Описать процедуру translate(infix,postfix), которая переводит выражение (определение "выражения" смотри в задаче 12), записанное в обычной (инфиксной) форме в текстовом файле infix, в постфиксную форму и в таком виде записывает его в текcтовый файл postfix.
Использовать следующий алгоритм перевода. В стек записывается открывающая скобка, и выражение просматривается слева направо. Если встречается операнд (число или переменная), то он сразу переносится в файл postfix. Если встречается открывающая скобка, то она заносится в стек, а если встречается закрывающая скобка, то из стека извлекаются находящиеся там знаки операций до ближайшей открывающей скобки, которая также удаляется из стека, и все знаки (в порядке их извлечения) записываются в файл postfix. Когда же встречается знак операции, то из конца стека извлекаются (до ближайшей скобки, которая сохраняется в стеке) знаки операций, старшинство которых больше или равно старшинству данной операции, и они записываются в файл postfix, после чего рассматриваемый знак заносится в стек. В заключение выполняются такие же действия, как если бы встречалась закрывающая скобка.
14. Описать (нерекурсивную) процедуру infixprint(postfix), которая печатает в обычной (инфиксной) форме выражение (определение "выражения" смотри в задаче 12), записанное в постфиксной форме в текстовом файле postfix (лишние скобки желательно не печатать).
15. Сформировать файл из символов и с помощью очереди за один просмотр файла напечатать элементы файла в следующем порядке: сначала все символы, отличные от цифр, а затем все цифры, сохраняя исходный порядок в каждой из этих групп символов.
16. Сформировать файл из символов и с помощью очереди за один просмотр файла напечатать сначала все гласные буквы, затем знаки препинания и, наконец, - все согласные, сохраняя исходный порядок в каждой из этих групп символов.
17. В текстовом файле записана без ошибок формула вида: цифра или R(формула, формула), или L(формула, формула), где R обозначает функцию взять правое число, L-взять левое число. Вычислить значение данной формулы ( например, R (8, R (3, L (4,5)))=4 ).
18. Сформировать файл из натуральных чисел и с помощью очереди за один просмотр файла напечатать элементы файла в следующем порядке: сначала все однозначные числа, затем двузначные, сохраняя исходный порядок чисел в каждой из этих групп.
19. Сформировать файл из символов и с помощью очереди за один просмотр файла напечатать элементы файла напечатать элементы файла в следующем порядке: сначала все символы, отличные от знаков препинания и цифр, затем знаки препинания и наконец – все цифры, сохраняя исходный порядок в каждой из этих групп символов.
20. Сформировать файл из натуральных чисел и с помощью очереди за один просмотр файла напечатать элементы файла напечатать элементы файла в следующем порядке: сначала все числа, делящиеся на 5, затем все нечетные числа, не делящиеся на 5, и наконец – все четные числа, не делящиеся на 5, сохраняя исходный порядок в каждой из этих групп чисел.
21. В текстовом файле записана без ошибок формула вида: цифра или s(формула, формула) или p(формула, формула), где s (a , b) = (a + b) mod 10,
p (a,b) = (a*b) mod 10. Вычислить значение этой формулы.
Например, p (6, s (8, 4)) = 2.
22. Сформировать файл из натуральных чисел и с помощью очереди за один просмотр файла напечатать элементы файла в следующем порядке: сначала все однозначные числа, затем все двузначные. Первая группа чисел выводится в исходном порядке, вторая - в обратном порядке. Например: 2, 15, 7, 24, 37, 8 ® 2, 7, 8, 37, 24, 15.
23. Сформировать файл из символов и с помощью очереди за один просмотр файла напечатать элементы файла в следующем порядке: сначала все знаки препинания в исходном порядке, затем все согласные в обратном порядке, затем все согласные в обратном порядке, и наконец – все гласные в исходном порядке.
24. В текстовом файле записана без ошибок формула вида: цифра или m(формула, формула) или p(формула, формула), где m ( a , b ) = ( a - b ) mod 10,
p (a, b) = (a+b) mod 10. Вычислить значение этой формулы.
Например, m (9, p ( p (3, 5), m (3, 8))) = 6.
В упражнениях 25-33 использовать двоичные деревья при следующем их описании.
type ТЭД= ... : {тип элементов дерева}
дерево= ^ вершина;
вершина=record элем:ТЭД;
лев, прав:дерево end;
В этих упражнениях Т,  и
и 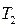 обозначают деревья, а Е – величину типа ТЭД.
обозначают деревья, а Е – величину типа ТЭД.
25. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая присваивает параметру Е элемент из самого левого листа непустого дерева Т (лист - вершина, из которого не выходит ни одной ветви). Продемонстрировать работу программы.
26. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая определяет число вхождений элемента Е в дерево Т. Продемонстрировать работу программы.
27. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая вычисляет среднее арифметическое всех элементов непустого дерева Т (ТЭД=real). Продемонстрировать работу программы.
28. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая заменяет в дереве Т все отрицательные элементы на их абсолютные величины (ТЭД=real). Продемонстрировать работу программы.
29. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая меняет местами максимальный и минимальный элементы непустого дерева Т, все элементы которого различны (ТЭД=real). Продемонстрировать работу программы.
30. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая печатает элементы из всех листьев дерева Т (ТЭД=char). Продемонстрировать работу программы.
31. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая печатает все элементы дерева Т по уровням ( сначала - из корня дерева, затем (слева направо) - из вершин, дочерних по отношению к корню, затем (также слева направо) - из вершин, дочерних по отношению к этим вершинам, и т.д.) (ТЭД=integer). Продемонстрировать работу программы.
32. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая находит в непустом дереве Т длину (число ветвей) пути от корня до ближайшей вершины с элементом Е; если Е не входит в Т, за ответ принять -1. Продемонстрировать работу программы.
33. Используя очередь или стек (предварительно описав его тип и операции над ним (упр.1 или упр.2)), описать процедуру или функцию, которая подсчитывает число вершин на n-ом уровне непустого дерева Т (корень считать вершиной 0-го уровня). Продемонстрировать работу программы.
Двоичные деревья
В упражнениях 1-27 использовать двоичные деревья при следующем их описании.
type ТЭД= ... : {тип элементов дерева}
дерево= вершина;
вершина=record элем:ТЭД;
лев, прав: дерево end;
В этих упражнениях Т, 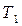 и
и 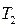 обозначают деревья, а Е – величину типа ТЭД.
обозначают деревья, а Е – величину типа ТЭД.
1. Создать и продемонстрировать работу программы, которая определяет, входит ли элемент Е в дерево Т.
2. Создать и продемонстрировать работу программы, которая определяет число вхождений элемента Е в дерево Т.
3. Создать и продемонстрировать работу программы, которая вычисляет сумму элементов непустого дерева Т (ТЭД=real ).
4. Создать и продемонстрировать работу программы, которая находит величину наибольшего элемента непустого дерева Т (ТЭД=real ).
5. Создать и продемонстрировать работу программы, которая печатает элементы из всех листьев дерева Т (ТЭД=char ).
6. Создать и продемонстрировать работу программы, которая определяет максимальную глубину непустого дерева Т, т.е. число ветвей в самом длинном из путей от корня дерева до листьев.
7. Создать и продемонстрировать работу программы, которая подсчитывает число вершин на n-ом уровне непустого дерева Т (корень считать вершиной 0-го уровня).
8. Рекурсивно и не рекурсивно создать и продемонстрировать работу логической функции equal (T1,T2), проверяющую на равенство деревья Т1 и Т2.
9. Создать и продемонстрировать работу процедуры copy(Т, Т1), которая строит Т1 - копию дерева Т.
10. Создать и продемонстрировать работу процедуры create(T,n), где n - положительное целое число, которое строит дерево Т, показанное на рис. 9.1.

11. Создать и продемонстрировать работу логической функции same(T), определяющую, есть ли в дереве Т хотя бы два одинаковых элемента.
12. Формулу вида
<формула> ::= <терминал> ï (<формула><знак><формула>)
<знак> :: = + ï - ï *
<терминал> ::= 0 ï 1 ï 2 ï 3 ï 4 ï 5 ï 6 ï 7 ï 8 ï 9
можно представить в виде двоичного дерева ("дерева-формулы") с ТЭД=char согласно следующим правилам: формула из одного терминала (цифры) представляется деревом из одной вершины с этим терминалом, а формула вида (f1 s f2) - деревом, в котором корень - это знак s, а левое и правое поддеревья - это соответствующие представления формул f1 и f2. На рис. 9.2 показано дерево-формула, соответствующее формуле (5*(3+8)).
Создать и продемонстрировать работу программы, которая вычисляет (как целое число) значение дерева-формулы Т.
 |
13. Создать и продемонстрировать работу программы, которая по формуле (см. упр.12) из текстового файла f строит соответствующее дерево-формулу Т.
14. Создать и продемонстрировать работу программы, которая печатает дерево-формулу Т (см. упр.12) в виде соответствующей формулы.
15. Создать и продемонстрировать работу программы, которая проверяет, является ли двоичное дерево Т деревом-формулой (см. упр.12).
16. Пусть в дереве-формуле (см. упр.12) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая упрощает дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам (f+1), (0+f ), (f-0),
(f*1) и (1*f), на поддеревья, соответствующие формуле f, а поддеревья, соответствующие формулам (f*0) и (0*f ), - на вершину с 0.
17. Пусть в дереве-формуле (см. упр.12) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам ((f1+f2)*f3,
(f1-f2)*f3, f1*(f2+f3), f1*(f2-f3)) на поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3), (f1*f2)+(f1*f3), (f1*f2)-(f1*f3)).
18. Пусть в дереве-формуле (см. упр.12) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3), (f1*f2)+(f1*f3), (f1*f2)-(f1*f3)) на поддеревья, соответствующие формулам ((f1+f2)*f3, (f1-f2)*f3, f1*(f2+f3), f1*(f2-f3)).
19. Пусть в дереве-формуле (см. упр.12) в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая строит дерево-формулу Т1 - производную дерева-формулы Т по переменной, однобуквенное имя которой является значением литерного параметра v.
20. Предложить и описать на Паскале представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Создать и продемонстрировать работу программы, которая вычисляет (как целое число) значение дерева-формулы Т.
21. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Создать и продемонстрировать работу программы, которая по формуле из текстового файла f строит соответствующее дерево-формулу Т.
22. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Создать и продемонстрировать работу программы, которая печатает дерево-формулу Т в виде соответствующей формулы.
23. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Создать и продемонстрировать работу программы, которая проверяет, является ли двоичное дерево Т деревом-формулой.
24. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Пусть в дереве-формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая упрощает дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам (f+1), (0+f), (f-0), (f*1) и (1*f), на поддеревья, соответствующие формуле f, а поддеревья, соответствующие формулам (f*0) и (0*f), - на вершину с 0.
25. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Пусть в дереве-формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам ((f1+f2)*f3,
(f1-f2)*f3, f1*(f2+f3), f1*(f2-f3)) на поддеревья, соответствующие формулам ((f1*f3)+(f2*f3), (f1*f3)-(f2*f3), (f1*f2)+(f1*f3), (f1*f2)-(f1*f3)).
26. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Пусть в дереве-формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая преобразует дерево-формулу Т, заменяя в нем все поддеревья, соответствующие формулам ((f1*f3)+(f2*f3),
(f1*f3)-(f2*f3), (f1*f2)+(f1*f3), (f1*f2)-(f1*f3)) на поддеревья, соответствующие формулам ((f1+f2)*f3, (f1-f2)*f3, f1*(f2+f3), f1*(f2-f3)).
27. Предложить и описать представление в виде двоичного дерева для формул из упр.12, в которых в качестве терминалов используются любые неотрицательные целые числа. Пусть в дереве-формуле в качестве терминалов используются не только цифры, но и буквы, играющие роль переменных. Создать и продемонстрировать работу программы, которая строит дерево-формулу Т1 - производную дерева-формулы Т по переменной, однобуквенное имя которой является значением литерного параметра v.
28. Деревом поиска, или таблицей в виде дерева, называется двоичное дерево, в котором слева от любой вершины находятся вершины с элементами, меньшими элемента из этой вершины, а справа - с большими элементами (предполагается, что все элементы дерева попарно различны и что их тип (ТЭД) допускает применение операций сравнения). Пример такого дерева показан на рис. 9.2.
Описав тип дерево (см. выше) и тип файл:
type файл=file of ТЭД;
написать и продемонстрировать программу, которая проверяет, входит ли элемент Е в дерево поиска Т.
29. Тип дерево и тип файл, такие же, как в упр 28. Написать и продемонстрировать программу, которая записывает в файл f элементы дерева поиска Т в порядке их возрастания.
30. Тип дерево и тип файл, такие же как в упр 28. Написать и продемонстрировать программу, которая добавляет к дереву поиска Т новый элемент Е, если его не было в Т.
31. Тип дерево и тип файл, такие же как в упр 28. Написать и продемонстрировать программу, которая по файлу f, все элементы которого различны, строит соответствующее дерево поиска Т.
32. Во внешнем текстовом файле PROG записана (без ошибок) некоторая программа на языке Паскаль. Известно, что в этой программе каждый идентификатор (служебное слово или имя) содержит не более 9 латинских букв и/или цифр. Напечатать в алфавитном порядке все различные идентификаторы этой программы, указав для каждого из них число его вхождений в текст программы. (Учесть, что в идентификаторах одноименные прописные и строчные буквы отождествляются, что внутри литерных значений, строк-констант и комментариев последовательности из букв и цифр не являются идентификаторами и что в записи вещественных чисел может встречаться буква Е или е).
Для хранения идентификаторов использовать дерево поиска, элементами которого являются пары - идентификатор и число его вхождений в текст программы.
33. Решить предыдущую задачу, но вместе с каждым идентификатором печатать в возрастающем порядке номера всех строк текста программы, в которых он встречается.
34. Решить задачу 32 при условии, что максимальная длина идентификаторов заранее не известна.
35. Решить задачу 33 при условии, что максимальная длина идентификаторов заранее не известна.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Берзтисс А.Т. Структуры данных. - М.: Статистика, 1974.
2. Трамбле Ж., Соренсон П. Введение в структуры данных. - М.: Машиностроение, 1982.
3. Вирт Н. Алгоритмы + структуры данных = программы. - М.: Мир, 1985.
4. Костин А.Е., Шаньгин В.Ф. Организация и обработка структур данных в вычислительных системах. - М.: Высшая школа, 1987.
5. Липский В. Комбинаторика для программистов. – М.: Мир, 1988.
6. Абрамов С.А. и др. Задачи по программированию. – М.: Наука, 1988.
7. Вирт Н. Алгоритмы и структуры данных. - М.: Мир, 1989.
8. Иенсон К., Вирт Н. Паскаль. Руководство для пользователя. - М.: Финансы и статистика, 1989.
9. Пильщиков В.С. Сборник упражнений по языку Паскаль: Учеб. пособие для вузов. - М.: Наука, 1989.
10. Попов А.А. Программирование в среде СУБД FoxPro 2.0. – М.: Радио и связь, 1994.
11. Воробович Н.П. Введение в структуры данных. - Красноярск: СТИ, 1994.
СОДЕРЖАНИЕ
|
| ||
| Введение | 3 | |
| 1. | Основные понятия о типах и структурах данных | 4 |
| 2. | Простейшие статические структуры | 7 |
| 2.1. Характерные свойства статических структур | 7 | |
| 2.2. Векторы | 8 | |
| 2.3. Массивы | 9 | |
| 2.4. Записи | 13 | |
| 2.5. Таблицы | 15 | |
| 3. | Полустатические структуры | 17 |
| 3.1. Общее понятие списковой структуры | 17 | |
| 3.2. Стеки | 18 | |
| 3.3. Очереди | 20 | |
| 3.4. Деки | 21 | |
| 4. | Линейные динамические структуры | 22 |
| 4.1. Характерные черты динамических структур | 22 | |
| 4.2. Односвязные списки | 22 | |
| 4.3. Двусвязные списки | 24 | |
| 4.4. Организация и представление линейных связных списков в памяти ЭВМ | 28 | |
| 4.5. Представление стеков, очередей и деков линейными списками | 29 | |
| 5. | Нелинейные связные структуры | 30 |
| 5.1. Обобщенные двусвязные списки | 30 | |
| 5.2. Многосвязные списки | 30 | |
| 5.3. Сетевые структуры | 31 | |
| 5.4. Деревья | 31 | |
| 5.5. Бинарные деревья | 33 | |
| 6. | Строковые данные | 34 |
| 6.1. Строки | 34 | |
| 6.2. Векторное представление строк | 35 | |
| 6.3. Списковое представление строк | 37 | |
| 7. | Файлы | 39 |
| 7.1. Организация файлов на устройствах внешней памяти | 39 | |
| 7.2. Основные типы файлов | 40 | |
| 7.3. Последовательные файлы | 41 | |
| 7.4. Библиотечные файлы | 42 | |
| 7.5. Файлы прямого доступа | 43 | |
| 7.6. Индексно-последовательные файлы | 49 | |
| 8. | Системы управления базами данных | 52 |
| 8.1. Сущность базы данных и системы управления базами данных | 52 | |
| 8.2. Классификация банков данных и их составных частей | 58 | |
| 8.3. Иерархическая и сетевая модели баз данных | 60 | |
| 8.4. Реляционная модель базы данных | 67 | |
| 9. | Задачи и упражнения | 73 |
| 9.1. Векторы | 73 | |
| 9.2. Матрицы | 81 | |
| 9.3. Строки | 90 | |
| 9.4. Записи и таблицы | 94 | |
| 9.5. Списки | 97 | |
| 9.6. Очереди, стеки, деки | 104 | |
| 9.7. Двоичные деревья | 112 | |
| Библиографический список | 118 | |
ВОРОБОВИЧ НИКОЛАЙ ПЕТРОВИЧ
Структуры данных
Учебное пособие
Отв. редактор проф. Г.А.Доррер
Редактор РИО С.К.Патюкова
Техн.редактор Т.П.Попова
__________________________________________________________
Подписано в печать Сдано в производство
Формат 60´84 1/16 Бумага типографская
Печать офсетная Усл.печ.л. 7,5 Усл.изд.л. 7,5
Изд. N 246 Тираж 100 экз. Заказ
Лицензия ИД 06543 от 16.01.02 г.
__________________________________________________________
Редакционно-издательский отдел, типография СибГТУ
650049, Красноярск, пр.Мира 82.
Дата: 2019-02-19, просмотров: 483.
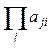 для всех таких j, что 1<aji£n;
для всех таких j, что 1<aji£n;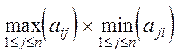 .
.