Кр = amax / amin ,
где a max, — максимальное значение ряда; a min, — минимальное значение ряда.
Если Кр <1,3, то очистку ряда производить не следует. В данном случае все значения ряда равновероятны и пригодны к расчёту средней величины (продолжительности) данного элемента рабочего процесса. Без дальнейшей проверки рассчитывается среднеарифметическое значение ряда.
Если 1,3< Кр <2 — ряд нуждается в дальнейшей проверке на возможность присутствия в нём случайных замеров. Проверка осуществляется методом предельных значений.
Если Кр > 2 — ряд нуждается в дальнейшей проверке, для которой применяют метод относительной средней квадратичной ошибки (ОСКО) среднего значения ряда.
Проверка ряда по методу предельных значений. Сущность метода заключается в сопоставлении наиболее отличающихся значений в исследуемом ряду с допустимыми и в решении вопроса о возможности сохранения проверяемого значения в ряду.
Определение допустимых наибольшего и наименьшего значения ряда осуществляется по следующим формулам:
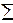 ai - an
ai - an
 anmax = + Klim (an-1 – a1),
anmax = + Klim (an-1 – a1),
n - 1
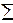 ai – a1
ai – a1
 a1min = - Klim (an – a2),
a1min = - Klim (an – a2),
n - 1
где 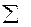 a i — сумма всех значений ряда; n — число значений в ряду; а n— наибольшее значение упорядоченного ряда; a1 — наименьшее значение упорядоченного ряда; К lim — коэффициент, зависящий от числа значении в ряду, определяемый по таблице.
a i — сумма всех значений ряда; n — число значений в ряду; а n— наибольшее значение упорядоченного ряда; a1 — наименьшее значение упорядоченного ряда; К lim — коэффициент, зависящий от числа значении в ряду, определяемый по таблице.
Таблица
| Число значений в ряду (n-1) | Кlim | Число значений в ряду (n-1) | Кlim |
| 4 5 6 7-8 | 1,4 1,3 1,2 1,1 | 9-10 11-15 16-30 31-50 | 1 0,9 0,8 0,7 |
Проверка ряда по методу относительной средней квадратичной ошибки (ОСКО) состоит в определении величины фактической относительной средней квадратичной ошибки ряда и в сравнении ее с допустимой величиной ошибки. Этот метод применяют для оценки нормативного ряда при Кр > 2.
Фактическую относительную среднюю квадратичную ошибку Еф проверяемого ряда определяют по формулам:
1
 E ф =
E ф = 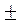
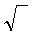 n
n 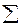 ai2 – (
ai2 – ( 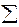 ai) 2 / n – 1 * 100,
ai) 2 / n – 1 * 100,
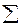 ai
ai
или
1
 E ф =
E ф = 
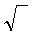
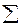
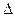 2 / n(n – 1) * 100,
2 / n(n – 1) * 100,
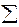 a ср
a ср
где 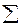
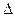 2 =
2 = 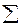 ( ai - a ср ) 2 — сумма квадратов отклонений каждого значения ряда от его среднего значения.
( ai - a ср ) 2 — сумма квадратов отклонений каждого значения ряда от его среднего значения.
Величина допустимой среднеквадратичной ошибки простого среднего арифметического значения ряда в зависимости от числа цикличных элементов в составе работ производственного процесса определяется по таблице.
Таблица
| Число цикличных элементов в составе работ | Допустимая величина ошибки (Едоп) среднего значения ряда ( + %) |
| До 5 Более 5 | 7 10 |
Если ошибка более допустимой, то необходимо исключить из ряда одно из крайних значений. Для установления, какое именно, рассчитывается К1 и К n :
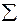 ai – a1
ai – a1
 K1 = ,
K1 = ,
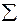 ai – an
ai – an
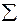 ai2 – a1
ai2 – a1 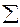 ai
ai
 Kn = ,
Kn = ,
an 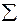 ai –
ai –  ai 2
ai 2
В случае: если К1<К n, то исключается первое (наименьшее) значение упорядоченного ряда (а1);
если К1>К n, то исключается последнее (наибольшее) значение упорядоченного ряда (а n).
После очистки и завершения проверки ряда рассчитывают, среднее значение по оставшимся значениям ряда.
Для простоты расчета можно использовать вспомогательную таблицу.
Таблица
| № | 1 | 2 | 3 | 4 | … | … | 10 | n-1 | n | 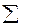
|
| ai | a1 | … | … | … | … | … | … | … | … | 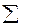 ai ai
|
| ai2 | a12 | … | … | … | … | … | … | … | … | 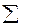 ai2 ai2
|
Пример: Проверить следующий ряд: 18, 23, 27, 16, 23, 13, 25, 22, 32, 21 при семи цикличных элементах состава работ Eдоп = 10%, Кр = 32/13 = 2,46.
Дальнейший расчет приведен в таблице.
Таблица
| П | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Сум- ма | Обозна- чение |
| ai ai2 | 13 169 | 16 256 | 18 314 | 21 441 | 22 484 | 23 529 | 23 529 | 25 625 | 27 729 | 32 1024 | 220 5110 | 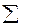 a1 a1
 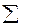 a12 a12
|
E ф = 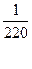
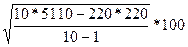 =
= 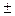
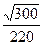
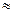
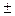 8% .
8% .
Так как 8 % < 10 %, то ряд очистки не требует.
Дата: 2019-02-19, просмотров: 403.