НОРМИРОВАНИЕ ТОЧНОСТИ И ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ
Лекция по нормированию точности техническим измерениям
Метрологические основы технических измерений
ЗАКОН РЕСПУБЛИКИ БЕЛАРУСЬ
Об обеспечении единства измерений (принят 5 сентября 1995 г. № 3848-XІІ)
Новая редакция Закона Республики Беларусь от 20 июля 2006 г. № 163-З (Национальный реестр правовых актов Республики Беларусь, 2006 г., № 122, 2/1260)
Изменения и дополнения:
Закон Республики Беларусь от 9 ноября 2009 г. № 53-З (Национальный реестр правовых актов Республики Беларусь, 2009 г., № 276, 2/1605);
Закон Республики Беларусь от 4 января 2010 г. № 109-З (Национальный реестр правовых актов Республики Беларусь, 2010 г., № 17, 2/1661);
Закон Республики Беларусь от 4 января 2014 г. № 130-З (Национальный правовой Интернет-портал Республики Беларусь, 23.01.2014, 2/2128)
Закон определяет правовые и организационные основы обеспечения единства измерений в Республике Беларусь и направлен на защиту прав и законных интересов граждан и государства от последствий неточных и неправильно выполненных измерений.
ГЛАВА 1
ОБЩИЕ ПОЛОЖЕНИЯ
В статье 1 приводятся основные термины, используемые в Законе и их определения
Единство измерений – состояние измерений, при котором их результаты выражены в единицах измерений, допущенных к применению в Республике Беларусь, и точность измерений находится в установленных границах с заданной вероятностью
Государственный метрологический надзор – деятельность по проверке и мониторингу соблюдения юридическими лицами и индивидуальными предпринимателями законодательства Республики Беларусь об обеспечении единства измерений;
Государственный реестр национальных эталонов единиц величин Республики Беларусь – совокупность сведений, формируемых Государственным комитетом по стандартизации Республики Беларусь, о национальных эталонах единиц величин;
Государственный реестр средств измерений Республики Беларусь – совокупность сведений, формируемых Государственным комитетом по стандартизации Республики Беларусь, о средствах измерений, в отношении которых принято решение об утверждении типа средств измерений, и о выданных сертификатах об утверждении типа средств измерений;
единица измерения;
измерение – как совокупность операций, выполняемых для определения значения величины;
калибровка – как составная часть метрологического контроля, включающая выполнение работ, в ходе которых устанавливаются метрологические характеристики средств измерений путем определения в заданных условиях соотношения между значением величины, полученным с помощью средства измерений, и соответствующим значением величины, воспроизводимым эталоном единицы величины;
методика выполнения измерений – совокупность правил и процедур выполнения измерений, которые обеспечивают получение результатов измерений, точность которых находится в установленных границах с заданной вероятностью;
метрологическая аттестация средств измерений – составная часть метрологического контроля, включающая выполнение работ, в ходе которых устанавливаются метрологические характеристики средств измерений;
метрологическая служба – совокупность организационно и (или) функционально связанных между собой юридических лиц, их структурных подразделений либо структурное подразделение юридического лица, деятельность которых направлена на обеспечение единства измерений;
метрологический контроль – совокупность работ, в ходе выполнения которых устанавливаются или подтверждаются метрологические, технические характеристики средств измерений, определяется соответствие средств измерений, методик выполнения измерений требованиям законодательства Республики Беларусь об обеспечении единства измерений, а также соответствие методик выполнения измерений своему назначению;
метрологическое подтверждение пригодности методик выполнения измерений – составная часть метрологического контроля, включающая выполнение работ, в ходе которых определяется соответствие методик выполнения измерений требованиям законодательства Республики Беларусь об обеспечении единства измерений, а также их соответствие своему назначению;
национальный метрологический институт как юридическое лицо, подчиненное Государственному комитету по стандартизации Республики Беларусь, на которое возложены проведение фундаментальных и прикладных научных исследований в области обеспечения единства измерений, хранение и применение национальных эталонов единиц величин в целях обеспечения прослеживаемости результатов измерений до единиц измерений Международной системы единиц, принятой Генеральной конференцией мер и весов и рекомендованной Международной организацией законодательной метрологии (далее – Международная система единиц), и иные функции в соответствии с настоящим Законом;
национальный эталон единицы величины – эталон единицы величины, утвержденный решением Государственного комитета по стандартизации Республики Беларусь в качестве национального эталона единицы величины;
обеспечение единства измерений –как деятельность, направленная на достижение и поддержание единства измерений в соответствии с требованиями законодательства Республики Беларусь об обеспечении единства измерений;
поверитель – физическое лицо, являющееся работником юридического лица или индивидуального предпринимателя либо индивидуальным предпринимателем и подтвердившее свою профессиональную компетентность в осуществлении поверки в соответствии с законодательством Республики Беларусь об оценке соответствия;
поверка – составная часть метрологического контроля, включающая выполнение работ, в ходе которых подтверждаются метрологические характеристики средств измерений и определяется соответствие средств измерений требованиям законодательства Республики Беларусь об обеспечении единства измерений;
система обеспечения единства измерений Республики Беларусь как комплекс мер по государственному регулированию и управлению, государственному метрологическому надзору и метрологическому контролю, осуществляемых государственными органами, юридическими лицами, индивидуальными предпринимателями и иными физическими лицами в целях обеспечения единства измерений;
средство измерений как техническое средство, предназначенное для измерений, воспроизводящее и (или) хранящее единицу измерения, а также кратные либо дольные значения единицы измерения, имеющее метрологические характеристики, значения которых принимаются неизменными в течение определенного времени;
сфера законодательной метрологии – установленные Законом и иными законодательными актами Республики Беларусь сферы деятельности, в которых в целях обеспечения единства измерений осуществляются государственное регулирование и управление, а также государственный метрологический надзор;
составная часть метрологического контроля - утверждение типа средств измерений, включающая выполнение работ, в ходе которых на основании государственных испытаний средств измерений устанавливаются их метрологические и технические характеристики, определяется соответствие средств измерений требованиям законодательства Республики Беларусь об обеспечении единства измерений и принимается решение об утверждении типа средств измерений;
эталон единицы величины – средство измерений, утвержденное в соответствии с правилами, установленными Государственным комитетом по стандартизации Республики Беларусь, в качестве эталона единицы величины.
ГЛАВА 5
Статья 21. Права и обязанности органов государственного метрологического надзора, Главного государственного инспектора Республики Беларусь по государственному метрологическому надзору, государственных инспекторов при проведении проверок и мониторингов
ГЛАВА 6
МЕТРОЛОГИЧЕСКИЙ КОНТРОЛЬ
НА КАЧЕСТВО ИЗДЕЛИЙ
Очевидно, что качество изделий обеспечивает изготовитель. Если изделие сделано плохо, оно плохо работает. Но если разработано морально устаревшее изделие, оно будет неконкурентоспособным на рынке даже при отличном качестве изготовления. Следовательно, за качество отвечает и разработчик. Но неправильное использование изделия приведет к его быстрой поломке, и в таком случае, разговор о качестве теряет всякий смысл. В настоящее время особое внимание уделяют также утилизации изделий, поскольку опыт работы с такими объектами как атомные электростанции и атомные подводные лодки заставляет обращать внимание не только на эффективность функционирования, но и на угрозу загрязнения окружающей среды. Значит, качество изделия следует рассматривать на протяжении всего “жизненного цикла” от проектирования, через изготовление и эксплуатацию – до физической или моральной его “смерти”. “Жизненный цикл” изделия строится с учетом не только прямых связей (качество сложного изделия закладывается при проектировании, обеспечивается в ходе производства, реализуется при эксплуатации), но и обратных связей, которые используются для корректирования требований, обеспечивающих приемлемый уровень качества объекта.
При проектировании изделия определенный уровень качества закладывается еще на этапе технического задания. Качество любого объекта (проекта, изделия, процесса) можно оценить, и на основе этой оценки сравнить объекты одинакового назначения.
Качество изделия является наиболее общим его свойством и складывается из таких свойств как надежность, мощность, коэффициент полезного действия, эргономичность и др. В свою очередь, эти свойства могут быть более или менее сложными. Например, надежность изделия включает в себя его безотказность, долговечность, ремонтопригодность и сохраняемость. А такие свойства, как масса, отдельные габаритные размеры изделия являются простейшими и не разлагаются на составные элементы.
Простейшие свойства, которые могут быть выражены числовыми значениями физических величин: масса, длина, твердость и др. далее будут называться параметрами. Функциональные параметры элементов изделия — это параметры, определяющие уровень его эксплуатационных показателей. К ним могут быть отнесены геометрические, физико-механические, электрические, магнитные и другие.
Номенклатура функциональных параметров зависит от назначения изделия, его состава, конструкции и работы. Например, от площади зазоров в системе цилиндр-кольцо-поршень и объема камеры сгорания зависит вращающий момент двигателя внутреннего сгорания. От твердости рабочих поверхностей уплотнительных колец и стенок цилиндра зависит их износостойкость, следовательно, и долговечность двигателя. Подобные примеры легко найти в любом техническом изделии.
Эксплуатационные показатели, определяющие качество изделий, зависят в значительной степени от геометрических параметров деталей. Для нормальной работы соединений деталей (сопряжений) и изделия в целом необходимо обеспечить требуемую точность размеров, формы и расположения поверхностей, а также параметры их микрогеометрии (шероховатости).
Для большинства деталей необходимо соблюдать требуемую точность не только по геометрическим параметрам. Например, наиболее важные детали оптико-механического прибора (микроскопа, фотоаппарата, бинокля) изготавливаются из стекла или пластмасс, и для них весьма существенны оптические свойства материала. Точность присоединительных размеров оптических деталей также будет влиять на качество собранного изделия. Кроме того, оптические свойства самих деталей в значительной мере зависят от точности таких геометрических параметров, как радиусы и толщина линз, углы и толщина призм, а также от правильности формы и микрогеометрии сферических и плоских поверхностей линз и зеркал, их расположения и т.д.
Поверхность шарика в пишущем узле стержня шариковой ручки должна быть достаточно правильной (сферической) для того, чтобы шарик свободно вращался, а размеры шарика и гнезда должны обеспечивать зазор для выхода красящей пасты. Причем, слишком маленький зазор приведет к заклиниванию при письме, а слишком большой – к свободному вытеканию пасты на бумагу, в карман или сумку, где лежит ручка.
Из рассмотренных примеров видно, что геометрические параметры в значительной степени влияют на качество любого изделия вне зависимости от сферы его применения и целевого назначения (от механической детской игрушки до космического корабля).
Множество современных технических изделий работает на автономном электрическом питании от батареек. Батарейки вставляют в часы, фотоаппараты, фонари, игрушки, причем вставить новую батарейку часто может сам пользователь. Замена наиболее часто употребляемых батарей возможна благодаря тому, что во всем мире изготовители и пользователи придерживаются одинаковых норм – стандартов – на их геометрические размеры и напряжение. Поэтому гнезда в приборах и игрушках позволяют легко установить туда подходящие батарейки в необходимом количестве.
Весь мир пользуется фотографической пленкой стандартных размеров, то же можно сказать о магнитных пленках для аудио- и видеоаппаратуры, дискетах и компакт-дисках.
Взаимозаменяемость однородных изделий означает “одинаковость” их основных параметров. Но единообразие подхода к нормированию параметров не исключает возможности разработки и выпуска различающихся изделий одного назначения. Необходимость применения разнообразных по видам и числовым значениям параметров требует разработки систем допусков, причем в первую очередь стандартизации подвергаются геометрические параметры деталей и сопряжений.
Для того чтобы запустить изделия в серийное и массовое производство, техническая документация на них должна содержать жестко нормированные значения основных функциональных параметров. Чтобы разбросы параметров, неизбежно возникающие при изготовлении элементов, не оказывали существенного влияния на работу изделия, их ограничивают определенными нормами. Параметры могут быть с одной стороны (сверху или снизу), но наиболее часто используют двухстороннее ограничение. Нормы допустимого рассеяния параметров при двухстороннем ограничении называют допусками.
Соблюдение единообразия номинальных значений параметров и норм их рассеяния обеспечивает взаимозаменяемость изделий. Нормы номинальных значений параметров могут быть зафиксированы в виде рядов предпочтительных чисел, а для геометрических параметров – в виде рядов нормальных линейных размеров, нормальных углов, уклонов и конусностей.
ОСНОВНЫЕ ЗАДАЧИ МЕТРОЛОГИИ
К основным задачам теоретической метрологии относятся:
- установление рациональной номенклатуры единиц физических величин;
- создание и совершенствование системы воспроизведения, хранения и передачи размеров единиц;
- установление номенклатуры, методов нормирования, оценки и контроля показателей точности результатов измерений и метрологических характеристик средств измерений;
- разработка оптимальных (в соответствии с принятыми для каждой измерительной задачи критериями оптимальности) принципов, приемов и способов обработки результатов измерения.
На практике задачи метрологии претворяют в жизнь специально созданные метрологические службы.
К основным задачам метрологической службы предприятия относятся:
- обеспечение единства и требуемой точности измерений, повышение уровня метрологического обеспечения производства;
- внедрение в практику современных методов и средств измерений, направленное на повышение уровня научных исследований, эффективности производства, технического уровня и качества продукции, а также иных работ, выполняемых предприятием;
- организация и проведение калибровки и ремонта средств измерений, находящихся в эксплуатации, своевременное представление средств измерений на поверку;
- проведение метрологической аттестации методик выполнения измерений, а также участие в аттестации средств испытаний и контроля.
- проведение метрологической экспертизы технических заданий, проектной, конструкторской и технологической документации, проектов стандартов и других нормативных документов;
- проведение работ по метрологическому обеспечению подготовки производства;
- участие в аттестации испытательных подразделений, в подготовке к аттестации производств и сертификации систем качества;
- осуществление метрологического надзора за состоянием и применением средств измерений, аттестованными методиками выполнения измерений, эталонами, применяемыми для калибровки средств измерений, соблюдением метрологических правил и норм, нормативных документов по обеспечению единства измерений.
МЕТОДЫ ИЗМЕРЕНИЙ
Совокупность приемов использования принципов и средств измерений составляет метод измерения. Различные методы измерений отличаются, прежде всего, организацией сравнения измеряемой величины с единицей измерения. С этой точки зрения все методы измерений подразделяются на две группы: методы непосредственной оценки и методы сравнения. Методы сравнения в свою очередь включают в себя метод противопоставления, дифференциальный метод, нулевой метод, метод замещения и метод совпадений.
При методе непосредственной оценки значение измеряемой величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия (измерительный прибор, в котором предусмотрено одно или несколько преобразований сигнала измерительной информации в одном направлении, т. е. без обратной связи). На этом методе основаны все показывающие (стрелочные) приборы (вольтметры, амперметры, ваттметры, счетчики электрической энергии, термометры, тахометры и т. п.). При использовании данного метода измерений мера как вещественное воспроизведение единицы измерения, как правило, непосредственно в процессе измерения не участвует. Сравнение измеряемой величины с единицей измерения осуществляется косвенно путем предварительной градуировки измерительного прибора с помощью образцовых мер или образцовых измерительных приборов.
Точность измерения по методу непосредственной оценки в большинстве случаев невелика и ограничивается точностью применяемых измерительных приборов.
Метод сравнения с мерой - это такой метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой. Примеры этого метода: измерение массы на рычажных весах с уравновешиванием гирь; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС нормального элемента.
Метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами, называется методом противопоставления. Это, например, измерение массы на рычажных весах с помещением ее и уравновешивающих гирь на две чашки весов при известном соотношении плеч рычага весов. В этом случае при качественном выполнении устройства сравнения (малое трение в опорах, стабильность соотношения плеч рычага и т. п.) может быть достигнута высокая точность измерений (например - аналитические весы).
Дифференциальный метод - это метод сравнения с мерой, в котором на измерительный прибор воздействует разность измеряемой величины и известной величины, воспроизводимой мерой. Этот метод позволяет получать результаты измерений с высокой точностью даже в случае применения относительно неточных измерительных приборов, если с большой точностью воспроизводится известная величина.
Эффект повышения точности результатов измерений, достигаемый при дифференциальном методе, оказывается тем значительнее, чем ближе значение меры к истинному значению измеряемой величины. В том случае, когда результирующий эффект воздействия величин на прибор сравнения доводя до нуля, дифференциальный метод измерений превращается в нулевой. В нулевом методе измерений используемая мера должна быть изменяемой (регулируемой), а прибор сравнения выполняет функции индикатора равенства нулю результирующего воздействия измеряемой величины и меры.
Нулевой метод позволяет получить высокие точности измерений и широко используется, например, при измерениях электрического сопротивления мостом с полным его уравновешиванием или постоянного напряжения компенсатора постоянного тока.
Методом замещения называется метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой. Это, например, взвешивание с поочередным помещением массы и гирь на одну и ту же чашку весов. Метод замещения можно рассматривать как разновидность дифференциального или нулевого метода, отличающуюся тем, что сравнение измеряемой величины с мерой производится разновременно.
Метод совпадений - это метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадения отметок шкал или периодических сигналов. Примерами этого метода являются измерения длины с помощью штангенциркуля с нониусом, измерение частоты вращения стробоскопом.
СРЕДСТВА ИЗМЕРЕНИЙ.
Единица длины
- метр – длина пути, которую проходит свет в вакууме за 1/299792458 долю секунды; (м).
Единица массы - килограмм - представлен массой международного прототипа килограмма (цилиндр из платино-иридия размерами 39 на 39 мм); (кг).
В 1899 году было изготовлено 43 образца, Россия получила 2 из них N12 и N26. Первый - Государственный эталон. Второй - эталон копия.
Напоминаем, что килограмм силы – это сила, сообщающая массе, равной массе международного прототипа килограмма, ускорение, равное 9,80665 м/с2; (Н).
Единица времени - секунда – продолжительность, равная 9 192 631 770 периодам излучения, которая соответствует переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133 при отсутствии возмущения со стороны внешних полей; (с).
Единица силы электрического тока - ампер - сила не изменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным на расстоянии 1м руг от друга в вакууме, вызвал бы на каждом участке проводника длиной 1м силу взаимодействия, равную 2·10-7 Н; (А).
Единица термодинамической температуры - кельвин – 1/273,16 часть термодинамической температуры тройной точки воды; допускается также применение шкалы Цельсия; (К).
Единица количества вещества – моль – количество вещества системы, содержащей столько же структурных элементов (атомов, молекул, электронов и др.), сколько атомов содержится в углероде-12 массой 0,012 кг; (моль).
Единица силы света – кандела – сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540·1012 Гц, энергетическая сила которого в этом направлении составляет 1/683 Вт/ср; (К).
Дополнительные:
Единица плоского угла - радиан - угол между двумя радиусами окружности, длина дуги между которыми равна радиусу; (рад). В градусном исчислении радиан равен 57º17'48
Единица телесного угла - стерадиан - угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы; (ср).
Радиан и стерадиан применяют в основном для теоретических построений и расчетов (например, в светотехнике – стерадиан), для практических прямых измерений их не используют, а плоские углы чаще всего измеряют в угловых градусах, минутах и секундах. Эти внесистемные единицы допущены к применению наравне с единицами Международной системы и в них градуировано большинство угломерных приборов.
В практике измерений часто применяют разрешенные внесистемные единицы например, для массы - тонна; для времени - минута, час, сутки, неделя, месяц, год, и т.д.
2. Модели измерительного процесса
Всякая реальная система, материальный объект характеризуется бесконечным числом переменных. Когда мы описываем, характеризуем систему, мы, исходя из своих предположений, делаем бесконечное число различных выборов из конечного числа переменных. Таким образом, фактически исследуется не подлинная система, не подлинное физическое явление, а его модель, в определенном смысле подобная истинной системе.
Модель - система, не отличимая от моделируемого объекта в отношении некоторых его свойств, именуемых существенными, и отличная от него в отношении других свойств, называемых несущественными.
В теории моделирования различают три принципиальных способа.
Полное моделирование - обеспечивается подобие движения материи во времени и пространстве. Различие между объектом исследования и моделью количественное, масштабное.
Неполное моделирование - здесь протекание основных процессов, характеризующих изучаемое явление или процесс, подобно только частично.
Приближенное моделирование - способ, применяемый наиболее часто, при котором некоторые факторы, влияющие на процесс, но не оказывающие на него решающего действия, либо вовсе не моделируются либо моделируются приближенно, грубо.
При современных исследованиях под моделью стали понимать и круг научных гипотез, позволяющих описывать известные и предсказывать новые явления.
Любое понятие, определенное через способ измерения или через другие сопоставимые и измеримые понятия, отделяется от своего прообраза и становится моделью.
Для получения оценок качества измерения и выработки требования к измерительной аппаратуре прибегают к моделям измерительного процесса, выделяя главные явления и факторы.
Каноническая модель измерительного процесса, понимаемого как эксперимент, условия которого строго определены и соблюдаются, строилась в метрологии при следующих ограничениях:
- измеряемая физическая величина сохраняет неизменным на протяжении всего цикла измерения свое истинное значение, которое можно охарактеризовать ее одним, так называемым действительным значением, лежащем внутри интервала остаточной неопределенности (доверительный интервал);
- время измерения не ограничено и сравнение с мерой может выполняться принципиально как угодно долго и тщательно;
- внешние условия и влияющие на результат факторы точно определены.
Но так как практические задачи измерительной техники отличаются от идеализированного метрологического эксперимента сравнения с мерой, то и изменяется модель измерительного процесса, т.е. производится оценка качества измерения на основе теоретически-вероятностного подхода.
Вероятностная модель измерительного процесса (информационная) - измеряемая физическая величина рассматривается как случайный процесс, содержащий интересующую нас информацию о состоянии исследуемого объекта и описывается случайной последовательностью действительных значений или же обобщенными характеристиками такой последовательности , истинное (мгновенное) значение измеряемой величины может оставаться неопределенным на данном интервале процесса измерения;
- измерение, в общем случае, рассматривается как последовательность операций, время выполнения которых ограничено и конечно; непосредственное сравнение с мерой неосуществимо;
- характеристики измерительного устройства могут изменяться во времени и под влиянием внешних факторов, переменных по своей природе /эти изменения рассматриваются как случайные процессы, влияющие на конечную неопределенность результата измерений/.
Указанные раньше основные группы классической модели являются частным случаем вероятностной модели. Необходимость введения вероятностной модели измерительного процесса вызвана прежде всего задачей оценки качества измерения меняющихся во времени величин (проблема динамической точности), которая не нашла удовлетворительного решения в рамках классической метрологии.
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
Погрешность измерений - это отклонение результата измерений от истинного значения измеряемой величины. Погрешность средств измерений зависит от условий проведения измерений. При этом различают основные и дополнительные погрешности.
Основная погрешность - погрешность, существующая при так называемых нормальных условиях, которые указаны в нормативных документах, регламентирующих правила испытания и эксплуатации данного средства измерений.
Дополнительная погрешность возникает при отклонении условий испытания и эксплуатации средства измерения от нормальных. Она нормируется значением погрешности, вызванной отклонением одной из влияющих величин от ее нормирующего значения или выходом ее за пределы нормальной области значений.
По способу выражения различают абсолютные и относительные погрешности.
Абсолютная погрешность измерения - погрешность измерений, выраженная в единицах измеряемой величины (1.1)
Относительная погрешность измерения - погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины, в процентах
d = D х / хд × 100%. (2.1)
Чтобы можно было сравнить по точности измерительные приборы с разными пределами измерений, введено понятие приведенной погрешности измерительного прибора, под которой понимают отношение абсолютной погрешности к нормирующему значению, которое принимается равным верхнему пределу измерений (если нулевая отметка находится на краю или вне шкалы) или диапазону измерения (если нулевая отметка находится внутри диапазона измерений), в процентах
g = (хизм - хд ) / хнор ×100%. (2.2)
Систематическая погрешность измерения - составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. В соответствии с этим определением систематические погрешности разделяются на постоянные и переменные. Переменные в свою очередь могут быть прогрессирующими, периодическими и изменяющимися по сложному закону.
Постоянными систематическими погрешностями называются такие, которые остаются неизменными в течение всей серии данных измерений, например, погрешность из-за неточной подгонки образцовой меры, погрешность из-за неточной установки указателя прибора на нуль и т. п.
Переменные систематические погрешности изменяются в процессе измерений. Если при измерениях погрешность монотонно убывает или возрастает, то она называется прогрессирующей. Так, например, монотонно меняется погрешность из-за разряда батареи или аккумулятора, если результат измерений зависит от напряжения питания. Периодическая систематическая погрешность - погрешность, значение которой является периодической функцией времени. Ее примером может являться погрешность, вызванная суточными изменениями напряжения питания электрической сети. Систематическая погрешность может изменяться и по некоторому сложному закону. Таковы, например, погрешности, вызванные неточностью нанесения шкалы прибора, погрешность электрического счетчика при различном значении нагрузки, погрешность, вызванная изменениями температуры окружающей среды, и др.
Случайная погрешность измерения - составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Например, погрешность измерений из-за вариации показаний измерительного прибора; погрешность округления, при считывании показаний измерительного прибора. Случайная погрешность не может быть исключена из результата измерения, но может быть уменьшена путем статистической обработки совокупности наблюдений.
Таким образом, погрешность результата измерения представляет собой сумму систематической и случайной составляющих.
Встречается также грубая погрешность или промах - погрешность измерения, существенно превышающая ожидаемую при данных условиях погрешность. Источником грубой погрешности может быть неправильный отсчет показаний средств измерений или непредвиденное кратковременное воздействие какого-либо фактора, например, резкое кратковременное изменение напряжения питающей сети. Грубые погрешности выявляются при статической обработке ряда наблюдений, и соответствующие результаты наблюдений должны быть исключены.
По зависимости от измеряемой величины погрешности средства измерений разделяют на аддитивные и мультипликативные.
Аддитивные (абсолютные) погрешности не зависят от измеряемой величины.
Мультипликативные (относительные) погрешности изменяются пропорционально измеряемой величине. Соответственно относительная аддитивная погрешность обратно пропорциональна значению измеряемой величины, а относительная мультипликативная - от него не зависит. Аддитивную погрешность иногда называют погрешностью нуля, а мультипликативную -погрешностью чувствительности. Реально погрешность средства измерений включает в себя обе указанные составляющие.
СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
Природа и происхождение систематических погрешностей обычно обусловлены спецификой конкретного эксперимента. Поэтому обнаружение и исключение систематических погрешностей во многом зависит от мастерства экспериментатора, от того, насколько глубоко он изучил конкретные условия проведения измерений и особенности применяемых им средств и методов. Вместе с тем существуют некоторые общие причины возникновения систематических погрешностей, в соответствии с которыми их подразделяют на методические, инструментальные и субъективные.
Методические погрешности происходят от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима исследуемого объекта (вследствие внесения термопары).
Инструментальные погрешности зависят от погрешностей применяемых средств измерений. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и т. д. являются причинами инструментальных погрешностей. Эта погрешность в свою очередь подразделяется на основную и дополнительную.
Основная погрешность средства измерений - это погрешность в условиях, принятых за нормальные, т. е. при нормальных значениях всех величин, влияющих на результат измерения (температуры, влажности, напряжения питания и т. п.).
Дополнительная погрешность средства измерений - погрешность, дополнительно возникающая при отличии значений влияющих величин от нормальных. Обычно различают отдельные составляющие дополнительной погрешности, например температурную погрешность, погрешность из-за изменения напряжения питания и т. п.
Все эти погрешности отличают от инструментальных (ГОСТ 8.009-84), поскольку они связаны не столько с самими средствами измерений, сколько с условиями, при которых они работают. Их устранение производится иными способами, нежели устранение инструментальных погрешностей.
Субъективные погрешности вызываются неправильными отсчетами показаний прибора человеком (оператором). Это может случиться, например, из-за неправильного направления взгляда при наблюдении за показаниями стрелочного прибора (погрешность от параллакса). Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности.
Обнаружение причин и источников систематических погрешностей позволяет принять меры к их устранению или исключению посредством введения поправки.
Поправкой называется значение величины, одноименной с измеряемой, которое нужно прибавить к полученному при измерении значению величины с целью исключения систематической погрешности.
В некоторых случаях используют поправочный множитель - число, на которое умножают результат измерения для исключения систематической погрешности.
Поправка или поправочный множитель определяется при помощи поверки технических средства, составления и использования соответствующих таблиц и графиков. Применяются также расчетные способы нахождения поправочных значений.
Существуют специальные методы организации измерений, устраняющие систематические погрешности. К ним относятся, например, метод замещения и метод компенсации погрешности по знаку. Метод замещения заключается в том, что измеряемая величина замещается известной величиной, получаемой при помощи регулируемой меры. Если такое замещение производится без каких-либо других изменений в экспериментальной установке и после замещения установлены те же показания приборов, то измеряемая величина равняется известной величине, значение которой отсчитывается по указателю регулируемой меры. Этот прием позволяет исключить постоянные систематические погрешности. Погрешность измерения при использовании метода замещения определяется погрешностью меры и погрешностью, возникающей при отсчете значения величины, замещающей неизвестную.
Метод компенсации погрешности по знаку применяется для исключения систематических погрешностей, которые в зависимости от условий измерения могут входить в результат измерения с тем или иным знаком (погрешность от термо-ЭДС, от влияния напряженности постоянного электрического или магнитного поля и др.). В этом случае можно провести измерения дважды так, чтобы погрешность входила в результаты измерений один раз с одним знаком, а другой раз - с обратным. Среднее значение из двух полученных результатов является окончательным результатом измерения, свободным от указанных выше систематических погрешностей.
При проведении автоматических измерений широко используются схемные методы коррекции систематических погрешностей. Компенсационное включение преобразователей, различные цепи температурной и частотной коррекции являются примерами их реализации.
Новые возможности появились в результате внедрения в измерительную технику средств, содержащих микропроцессорные системы. С помощью последних удается производить исключение или коррекцию многих видов систематических погрешностей. Особенно это относится к инструментальным погрешностям. Автоматическое введение поправок, связанных с неточностями градуировки, расчет и исключение дополнительных погрешностей, исключение погрешностей, обусловленных смещением нуля - это и другие корректировки позволяют существенно повысить точность измерений.
Следует, однако, заметить, что какая-то часть систематической погрешности, несмотря на все усилия, остается неисключенной. Эта часть входит в результат измерения и искажает его. Она может быть оценена исходя из сведений о метрологических характеристиках использованных технических средств. Если таких сведений недостаточно, то может быть полезным сравнение измеренных значений с аналогичными результатами, полученными в других лабораториях другими лицами.
СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
Теория погрешностей, использующая математический аппарат теории вероятностей, основывается на аналогии между появлением случайных погрешностей при многократно повторенных измерениях и появлением случайных событий. Из теории вероятностей известно, что для характеристики случайных величин, в нашем случае погрешностей прибора или измерения (вместе с их систематической составляющей), необходимо определить их закон распределения.
В теории случайных погрешностей формулируются две аксиомы.
Аксиома симметрии (случайности) - при очень большом числе измерений случайные погрешности, равные по величине, но различные по знаку, встречаются одинаково часто.
Аксиома распределения - чаще всего встречаются меньшие погрешности, а большие погрешности встречаются тем реже, чем они больше.
Если эти аксиомы соблюдаются, то при неограниченном увеличении числа независимых причин, вызывающих погрешности, мы имеем нормальный закон распределения случайной погрешности.
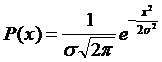 (2.3)
(2.3)
где P(х) - плотность вероятности случайной величины X; s - среднее квадратическое отклонение.
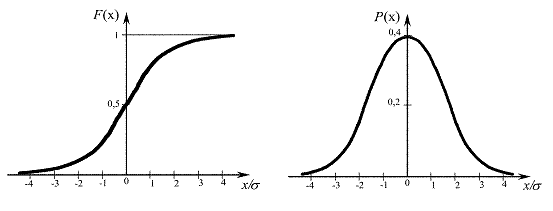
Рис. 2.1. Интегральный и дифференциальный законы распределения
Одно из нарушений нормального закона распределения погрешностей при соблюдении аксиом состоит в появлении плосковершинности и островершинности, как показано на рис. 2.2.
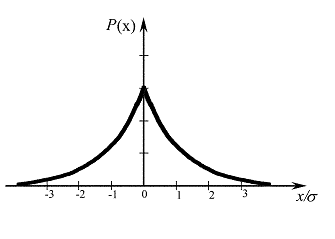
Рис. 2.2. Островершинное распределение
В пределе для плосковершинного распределения, когда уже аксиома не соблюдается, оно превращается в равномерное.
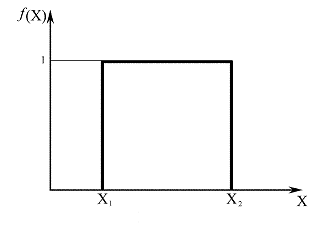
Рис. 2.3. Равномерное (равновероятное) распределение
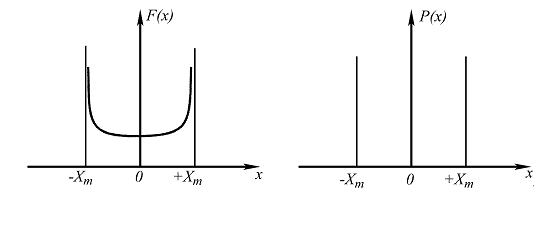
Рис. 2.4. Двухмодальное распределение
Модой дискретной случайной величины называют ее наиболее вероятное значение, а для непрерывной случайной величины модой является то значение, при котором плотность вероятности достигает максимума. В пределе такое двухмодальное распределение может превратиться в распределение, когда единственно наблюдаемыми погрешностями будут только погрешности ±XmaX (см. рис. 2.4). Например, погрешность от люфта в кинетической цепи, погрешность от гистерезиса имеют вид двухзначной дискретной погрешности.
ПРЯМЫХ ИЗМЕРЕНИЙ
Предположим, что истинное значение измеряемой величины равно а и выполнено n аналогичных измерений, результаты которых равны х1, х2,..., хn. Каждый из результатов хi, подлежащих совместной обработке для получения результата измерения, называют результатом наблюдения. Результатом измерения является оценка а значения измеряемой величины, вычисленная на основании всей совокупности результатов наблюдений х1, х2,..., хn. Разность Di = хi - а есть погрешность i-го наблюдения. Относительно этой погрешности сделаем следующие допущения:
- погрешность Di является случайной величиной с нормальным законом распределения;
- математическое ожидание погрешности М = 0, т.е. отсутствует систематическая погрешность;
- погрешность Di имеет дисперсию s2, одинаковую для всех измерений, т.е. измерения равноточные;
- погрешности отдельных наблюдений независимы.
Допущение о нормальности закона распределения погрешности основано на том, что случайная погрешность обычно вызывается целым рядом различных причин, а следовательно, какие бы законы распределения ни имели отдельные ее составляющие, при одинаковом порядке их малости закон распределения результирующей погрешности будет близок к нормальному.
Тогда плотность распределения любого результата хi запишется в виде
f = ( хi, a ) = e - (xi - a )^2 / 2 s^2 / Ö 2 p s.
Так как результаты отдельных наблюдений независимы, то плотность распределения системы случайных величин х1, х2,..., хn
n
f ( х1, х2,..., хn, а ) = Õ f ( хi, a ).
i = 1
Плотность распределения системы случайных величин и представляет собой функцию правдоподобия, которую обозначим
n é n ù
L = ( х1, х2,..., хn, а ) = Õ f ( хi, a ) = ( 2p ) -n/2 s-n exp ê- (1/ 2s2 ) å ( хi - a )2 ê. (2.6)
i = 1 ë i = 1 û
Использовав метод максимального правдоподобия, найдем оценку а таким образом, чтобы при а = а достигалось
L ( х1, х2,..., хn, а ) = max. (2.7)
Отсюда получим
n
а = ( 1/ n ) å хi = х, (2.10)
i = 1
т.е. наилучшей оценкой является среднее значение х результатов наблюдений.
Из (2.10) следует, что оценка х является случайной величиной с нормальным законом распределения, причем
М = а, s2 = s2 / n. (2.11)
Таким образом, оценка х имеет более высокую точность, так как ее дисперсия в n раз меньше дисперсии отдельных измерений. Неопределенность результатов измерений характеризуется значением среднего квадратического отклонения погрешности, поэтому из (2.11) следует, что при усреднении результатов n наблюдений случайную погрешность уменьшают в Ö n раз.
Следует отметить, что эффект уменьшения случайной погрешности при усреднении результатов n наблюдений снижается при наличии корреляции между этими результатами. Дисперсия оценки х для коррелированных результатов наблюдений
n
s2 = ( s2 / n) ,
i j
где rij - коэффициент корреляции между результатами i -го и j-го наблюдений.
Полученная оценка а = х является состоятельной, несмещенной и эффективной.
Для оценки неопределенности величины а необходимо, используя те же экспериментальные данные, оценить значение дисперсии (или среднего квадратического отклонения) погрешности измерений. Для этого воспользуемся функцией правдоподобия (2 ), представив ее в виде
n é n ù
L = ( х1, х2,..., хn, а ,s2 ) = Õ f ( хi, a ) = ( 2p )-n/2 (s2 )-n/2 exp ê- (1/ 2s2 ) å ( хi - a )2 ê. (2.12)
i = 1 ë i = 1 û
На основе метода максимального правдоподобия найдем оценку s2 из условия
L ( х1, х2,..., хn, а, s2 ) = max. (2.13)
Для упрощения вычислений прологарфимируем (2.12)
n
i = 1
Так как логарифм является монотонной функцией, то значения s2, при которых функции ( 7 ) и ( 9 ) достигают экстремума, совпадают. Поэтому оценку дисперсии найдем из условия
¶ ln L ( х1, х2,..., хn, а, s2 ) /¶ s2 = 0. (2.15)
Продифференцировав (2.15) по s2 , получим
- (1 / n ) ( 1 / s2) + (1/ 2s4) å ( хi - a )2 = 0. (2.16.)
i = 1
n
s2 = ( 1 / n ) å ( хi - a )2. (2.17)
i = 1
Так как истинное значение а неизвестно, то воспользуемся его оценкой х, а соответствующую оценку дисперсии обозначим S2 :
n
S2 = ( 1 / n ) å ( хi - х )2. (2.18)
i = 1
Рассмотрим вопрос о смещенности полученной оценки S2.
Предварительно преобразуем (2.18):
n n n
S2 = ( 1 / n ) å ( хi2 - 2 х ( 1 / n ) å хi + ( х )2 = ( 1 / n ) å хi2 - ( х )2 . (2.19)
i = 1 i = 1 i = 1
é n ù n
М = М ê( 1 / n ) å хi2 ê - М = ( 1 / n ) å М - М =
ë i = 1 û i = 1
= ( 1 / n ) å ( s2 + а2 ) - ( s / n + а2) = s2 ( 1 - 1 / n ) = s2 . (2.20)
i = 1
lim М = s2 .
n®¥
Такая оценка называется асимптотически несмещенной.
Из (2.20) следует, что для ликвидации смещенности оценки достаточно ввести поправочный множитель n /( n - 1 ). Полученную несмещенную оценку обозначим s2:
^ n
s2 = n /( n - 1 ) S2 = n /( n - 1 ) å ( хi - х )2. (2.20)
i = 1
Использовав (2.20), можно записать другую формулу для расчета оценки, равносильную ей но более удобную для вычислений:
ë i = 1 û
Полученные выше оценки значений измеряемой величины и дисперсии погрешности являются точечными оценками. Рассмотрим оценивание этих величин с помощью доверительных интервалов.
Определим доверительный интервал для истинного значения а измеряемой величины.
Границы этого интервала зависят не только от оценки а = х измеряемой величины, но и от оценки s среднего квадратического отклонения погрешности. Поэтому для построения доверительного интервала необходимо воспользоваться распределением случайной величины
tn -1 = ( х - а ) / S Ö n - 1 = ( х - а ) / s Ö n. (2.22)
Обычно в таблицах приводятся значения ta для величины t, имеющей расределение Стьюдента с k = n - 1 степенями свободы, определяемые из условия
¥
ò f n - 1 ( t ) dt = a, (2.23)
ta
Подставив в (2.23) граничные значения ± ta, получим границы доверительного интервала для измеряемой величины:
х - ta s / Ö n а х + ta s / Ö n .
u = n S2 / s2 = ( n - 1 ) s2 / s2
распределена по закону C2n-1 с n - 1 степенями свободы. В таблицах приводятся значения C2a для величины u, имеющей C2-распределение с k = n - 1 степенями свободы, определяемые из условия
¥
ò f n - 1 ( u ) du = a, (2.24)
C2a
Подставив в (2.24) вместо u найденные граничные значения C2a1 и C2a2 , получим границы доверительного интервала для дисперсии:
n S2 / C2a1 s2 n S2 / C2a2
или
( n - 1 ) s2 / C2a1 s2 ( n - 1 ) s2 / C2a2
Виды ИВК
По назначению ИВК делятся на типовые, проблемные и специализированные. Типовые комплексы предназначены для решения широкого круга типовых задач автоматизации измерений, испытаний или исследований независимо от области применения. Проблемные комплексы разрабатываются для решения специфичной для конкретной области применения задачи автоматизации измерений. Специализированные ИВК предназначены для решения уникальных задач автоматизации измерений, для которых разработка типовых и специализированных комплексов экономически нецелесообразна.
Основными составными частями комплекса являются (рис. 7.15):
- компьютер с периферийными устройствами, подключенными к нему, в том числе и посредством компьютерной сети;
- програмное обеспечение, представляющее собой совокупность взаимосвязанных программ, написанных на алгоритмических языках разного уровня;
- интерфейс, организующий связь технических устройств ИВК с компьютером;
- формирователь испытательных сигналов, которыми воздействуют на объект измерения с целью получения измерительных сигналов. Каждый такой сигнал (например, на рис. 11..19 это i-й сигнал) вырабатывается с помощью последовательно соединенных ЦАП; и преобразователя "напряжение - испытательный сигнал" (ПНИС;);
- измерительные каналы (ИК), предназначенные для преобразования в цифровой код заданного числа сигналов (К - для первого ИК и L - для N-ro ИК). Структура ИК существенно зависит от решаемой задачи. Однако практически в любом случае каждый из них содержит аналоговый измерительный (АИП) и аналого-цифровой (АЦП) преобразователи. При обработке нескольких измерительных сигналов одним АЦП в состав комплекса включается коммутатор, предназначенный для поочередного подключения сигналов к входу АЦП. Коммутатор может включаться как после АИП (ИК1на рис. 11.19), так и перед ним (ИК N на рис. 7.15).
АИП предназначен для преобразования измерительного сигнала в сигнал, однородный с входным сигналом АЦП (т.е. в напряжение), и масштабирования (усиления или ослабления) его до уровня, необходимого для проведения операции аналого-цифрового преобразования с минимальной погрешностью. При наличии нескольких измерительных сигналов (К сигналов в ИК1 на рис. 7.15) АИП состоит из К независимых последовательно соединенных первичных преобразователей и управляемых компьютером масштабируемых усилителей. Если же измерительные сигналы являются однородными физическими величинами и могут быть поочередно выбраны (скоммутированы), то в ИК целесообразно использовать только один АИП (рис. 7.15 - ИК N). Он последовательно во времени проводит преобразование измерительного сигнала и последующее его масштабирование.
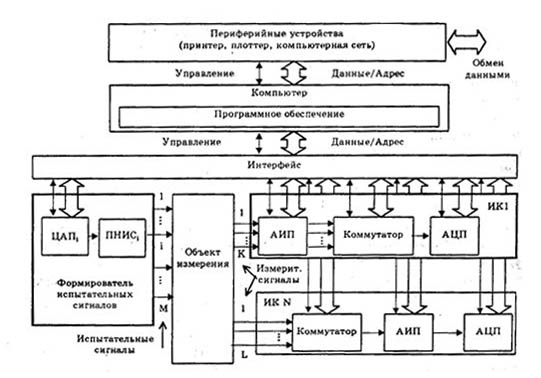
Рис.. Структурная схема измерительно-вычислительного комплекса
АЦП преобразует сигнал в цифровой код и передает его через интерфейс в компьютер. Работой всей аппаратной части ИВК управляет компьютер. Это осуществляется посредством:
- подачи управляющих сигналов различного рода;
- считывания и передачи по требуемым адресам цифровой информации (сигналы "Данные" и "Адрес" на рис. 7.15). Под "Адресом" понимается уникальный цифровой код, присвоенный конкретному блоку ИВК или его части и позволяющий компьютеру через интерфейс однозначно идентифицировать данное устройство.
По команде оператора выбирается тот или иной режим работы ИВК из числа реализованных в программном обеспечении. Компьютер рассчитывает цифровой код, описывающий заданное изменение во времени каждого из М испытательных сигналов, и в виде двоичного цифрового кода записывает в оперативные запоминающие устройства формирователя испытательных сигналов (на рис. 7.15 не показаны). Оттуда эти коды последовательно во времени циклически поступают на вход каждого из ЦАП. Формируемые на их выходах напряжения с помощью ПНИС преобразуются в требуемые физические величины, воздействующие на объект измерения.
Измерительные сигналы, представляющие собой отклик объекта измерения на испытательные воздействия, преобразуются в измерительных каналах в двоичный цифровой код и учитываются компьютером. Полученные коды обрабатываются по заданным алгоритмам, в результате получается искомая измерительная информация.
Каждый ИВК - это сложное техническое устройство, поэтому содержит средства диагностики его состояния
ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
Отдельные виды и типы средств измерений обладают своими специфическими свойствами. Вместе с тем средства измерений имеют некоторые общие свойства, которые позволяют сопоставлять средства между собой.
Различают статические и динамические свойства средства измерений.
Статические свойства средства измерений проявляются при статическом режиме его работы, т. е. когда выходной сигнал средства считается неизменным при измерении;
динамические свойства - при динамическом режиме работы средства измерений, при котором выходной сигнал средства изменяется во времени при его использовании.
Свойства средств измерений описывают характеристиками, среди которых выделяют комплекс метрологических характеристик.
Метрологические характеристики. Функция преобразования (статическая характеристика преобразования) - функциональная зависимость между информативными параметрами выходного и входного сигналов средства измерений. Функцию преобразования, принимаемую для средства измерения (типа) и устанавливаемую в научно-технической документации на данное средство (тип), называют номинальной функцией преобразования средства (типа).
Другой важной характеристикой является чувствительность средства измерений, под которой понимают отношение приращения выходного сигнала Dy средства измерений к вызвавшему это приращение изменению входного сигнала Dx. В общем случае чувствительность
S = lim Dy / Dx = dy / dx.
Dx®0
При нелинейной статической характеристике преобразования чувствительность зависит от входного сигнала х, при линейной характеристике чувствительность постоянна. У измерительных приборов при постоянной чувствительности шкала равномерная, т. е. длина всех делений шкалы одинакова. Деления шкалы - участки шкалы, на которые делят шкалу с помощью отметок.
Величина обратная чувствительности носит название постоянная прибора (С); C = 1 / S.
Порог чувствительности - это наименьшее изменение входной величины, обнаруживаемое с помощью данного средства измерений. Порог чувствительности выражают в единицах входной величины.
Диапазон измерений - область значений измеряемой величины, для которой нормированы допускаемые погрешности средства измерений. Диапазон измерений ограничивается наибольшим и наименьшим значениями диапазона измерений. С целью повышения точности измерений диапазон измерений средства измерений может быть разбит на несколько поддиапазонов. При переходе с одного поддиапазона на другой некоторые составляющие основной погрешности уменьшаются, что приводит к повышению точности измерений. При нормировании допускают для каждого поддиапазона свои предельные погрешности. Область значений шкалы, ограниченную начальными и конечными значениями шкалы, называют диапазоном показаний.
Характеристикой для измерительных приборов является цена деления шкалы - разность значений величины, соответствующих двум соседним отметкам шкалы. Для средства измерений, выдающих результаты измерений в цифровом коде, указывают цену единицы младшего разряда (единицы младшего разряда цифрового отсчетного устройства), вид выходного кода (двоичный, двоично-десятичный) и число разрядов кода.
Для оценки влияния средства измерений на режим работы объекта исследования указывают входное полное сопротивление Zвх. Входное сопротивление влияет на мощность, потребляемую от объекта исследования средством измерения. Допустимая нагрузка на средство измерений зависит от выходного полного сопротивления Zвых средства измерений. Чем меньше выходное сопротивление, тем больше допустимая нагрузка на средство измерений.
Важнейшей характеристикой средства измерений является погрешность, которую оно вносит в результат измерения, или, как принято говорить, погрешность средства измерений.
Погрешность средства измерений может быть выражена в виде абсолютной, относительной и приведенной погрешности.
Погрешность измерительного прибора:
Dx = х - хи, (1.1)
где х - показание прибора, хи - истинное значение измеряемой величины.
Погрешность измерительного прибора определяют при его поверке и при этом вместо истинного значения используют действительное значение измеряемой величины, под которым понимают значение физической величины, найденное экспериментальным путем с помощью образцовых средств измерений и настолько приближающееся к истинному, то для данной цели может быть использовано вместо истинного значения.
Погрешности средств измерений могут иметь систематические и случайные составляющие. Случайные составляющие приводят к неоднозначности показаний. Поэтому случайные составляющие погрешностей средств измерений стараются сделать незначительными по сравнению с другими составляющими. Большинство серийных измерительных приборов обладает этим свойством. Однако в приборах высокой чувствительности и точности случайная составляющая может быть соизмерима с систематической.
Важной характеристикой средств измерений является вариация выходного сигнала, под которой понимают разность между значениями информативного параметра выходного сигнала, соответствующими одному и тому же действительному значению входной величины при двух направлениях медленных изменений входной величины в процессе подхода к выбранному значению входной величины.
По зависимости от измеряемой величины погрешности средства измерений разделяют на аддитивные и мультипликативные.
Аддитивные (абсолютные) погрешности не зависят от измеряемой величины.
Мультипликативные (относительные) погрешности изменяются пропорционально измеряемой величине. Могут быть составляющие, имеющие более сложную зависимость от измеряемой величины, например, так называемые погрешности от нелинейности статической характеристики преобразования.
Различают погрешности конкретного экземпляра средства измерений и погрешности типа средств измерений. Тип средств измерений - совокупность средств измерений, имеющих одинаковые устройство, функциональное назначение и нормируемые характеристики.
Погрешность конкретного средства измерений характеризует только данный экземпляр средства измерений. Такая погрешность, обычно известная только для средств измерений, изготовленных в единичном экземпляре, или малой партией, или для специально поверенных средств измерений. Погрешность типа средств измерений характеризует всю совокупность экземпляров данного типа. Погрешность любого экземпляра данного типа не может превышать погрешности типа. Для приборов массового производства указывается погрешность типа.
Важным качеством средств измерений является их способность сохранять свои свойства во времени.
Для контроля метрологических свойств средства измерений должны периодически поверяться. Межповерочный интервал определяется нестабильностью свойств и допустимым изменением метрологических свойств средств измерений.
К метрологическим характеристикам средств измерений относятся динамические характеристики, т. е. характеристики инерционных свойств средства, определяющие зависимость выходного сигнала средства измерений от меняющихся во времени величин: параметров входного сигнала, внешних влияющих величин, нагрузки. Динамические свойства средства измерений определяют динамическую погрешность. В зависимости от полноты описания динамических свойств средств измерений, различают полные и частные динамические характеристики.
Полная динамическая характеристика - характеристика, однозначно определяющая изменения выходного сигнала средства измерений при любом изменении во времени информативного или неинформативного параметра входного сигнала, влияющей величины или нагрузки.
К полным динамическим характеристикам относят переходную характеристику, импульсную переходную характеристику, амплитудно-фазовую характеристику, совокупность амплитудно-частотной и фазово-частотной характеристик, передаточную функцию.
Частная динамическая характеристика не отражает полностью динамических свойств средств измерений. К частным динамическим характеристикам аналоговых средств измерений, которые можно рассматривать как линейные, относят любые функционалы или параметры полных динамических характеристик. Примерами таких характеристик являются время реакции средства измерений, коэффициент демпфирования, значение резонансной собственной угловой частоты, значение амплитудно-частотной характеристики на резонансной частоте.
Для измерительных приборов время реакции - время установления показаний прибора, т. е. время от момента скачкообразного изменения измеряемой величины до момента установления с определенной погрешностью показания, соответствующего установившемуся значению измеряемой величины.
Для измерительных преобразователей время реакции - время установления выходного сигнала, определяемое при скачкообразном изменении входного сигнала и заданной погрешности установления выходного сигнала.
Коэффициент демпфирования (степень успокоения) - параметр дифференциального уравнения второго порядка, описывающего линейное средство измерений.
Неметрологические характеристики. Кроме метрологических характеристик, при эксплуатации средств измерений важно знать и неметрологические характеристики: показатели надежности, электрическую прочность, сопротивление изоляции, устойчивость к климатическим и механическим воздействиям, время установления рабочего режима и др.
Под надежностью средства измерений понимают способность средства измерений сохранять заданные характеристики при определенных условиях работы в течение заданного времени или определенных условиях работы в течение заданного времени или заданной наработки. С понятием надежности связано понятие отказа - нарушения работоспособности средства измерений. Различают внезапный отказ, когда средство измерений полностью теряет свою работоспособность, например, вследствие обрыва цепи, и постепенный отказ, когда с течением времени метрологические характеристики выходят за допустимые пределы.
Согласно ГОСТ 22261-82 «Средства измерений электрических и магнитных величин. Общие технические условия» применяют следующие показатели надежности: безотказность, ремонтопригодность (для восстанавливаемых средств измерений), долговечность.
В качестве показателя безотказности устанавливают наработку на отказ. Под наработкой понимают продолжительность работы средства, а под наработкой на отказ - отношение наработки ремонтируемого средства к числу отказов в течение этой наработки.
В качестве показателя долговечности принят средний срок службы или средний ресурс. Срок службы и ресурс - соответственно календарная продолжительность эксплуатации средства и его наработка от ее начала до наступления такого предельного состояния, при котором дальнейшая эксплуатация средства должна быть прекращена.
В качестве показателя ремонтопригодности стандарт устанавливает среднее время восстановления средства
Стандарт организации
Система измерений в строительстве
ИЗМЕРЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ЗДАНИЙ И СООРУЖЕНИЙ И КОНТРОЛЬ ИХ ТОЧНОСТИ СТО НОСТРОЙ 37 - 2013
Окончательная редакция Фонд «Технического нормирования строительства» Москва 2013
Проект СТО НОСТРОЙ 37 - 2013
II Предисловие 1 РАЗРАБОТАН Фондом «Технического нормирования строительства» 2 ПРЕДСТАВЛЕН НА УТВЕРЖДЕНИЕ Комитетом по промышленному строительству Национального объединения строителей, протокол от 12 декабря 2012 года № 20 3 УТВЕРЖДЁН И ВВЕДЕН В ДЕЙСТВИЕ Решением Совета Национального объединения строителей от_______________ № ___ 4
ВВЕДЕН ВПЕРВЫЕ © Национальное объединение строителей, 2013
Распространение настоящего стандарта осуществляется в соответствии с действующим законодательством и с соблюдением правил, установленных Национальным объединением строителей
Проект СТО НОСТРОЙ 37 - 2013 III
Содержание
Введение …………………………………………………………………...... III
1 Область применения………………………………………………………... 1
2 Нормативные ссылки……………………………………………………….. 2
3 Термины и определения ….…………..……………………………………. 5
4 Принятые сокращения и обозначения…………………………………….. 10
5 Геометрические параметры зданий и сооружений. Виды измерений…. 15
5.1 Характеристики точности геометрических параметров строящихся зданий
и сооружений……………………………………………… ……… 15
5.2 Измерения по контролю точности геометрических параметров при выполнении видов строительных работ на этапах строительства… 19
5.3 Схемы геометрических параметров их отклонений подлежащих контролю на основе измерений при строительстве зданий и сооружений………………………………………………………………….. 26
6 Обеспечение точности измерений геометрических параметров зданий и сооружений………………………………………………………………….. 33
6.1 Требования по организации обеспечения точности измерений….. 33
6.2 Требования выбору средств, методик измерений, применяемых для измерения геометрических параметров…………………………….. 38
6.3 Условия измерения геометрических параметров зданий и сооружений…………………………………………………………………… 39
6.4 Требования к организация процесса измерения и применение характеристик качества измерений при контроле точности геометрического параметра при строящихся зданий и сооружений………. 41 7 Правила выполнения измерений………………………………………….... 44
7.1 Требования к выбору схем и методов измерения………………….. 44
7.2 Схемы и методы измерения линейных величин геометрических Проект СТО НОСТРОЙ 37 - 2013 IV параметров зданий и сооружений…………………………………… 45
7.3 Схемы и методы измерения угловых величин геометрических параметров зданий и сооружений………………………………………. 52
7.4 Схемы и методы измерения линейных и угловых величин геометрических параметров зданий и сооружений………………………… 55
7.5 Схемы и методы измерения линейных величин превышений между точками, отклонений точек конструкций зданий и сооружений…. 56
7.6 Схемы и методы измерения линейных величины отклонения от вертикальности конструкций, зданий и сооружений………………. 58
7.7 Схемы и методы измерения величины отклонений от заданного уклона, отклонений от прямолинейности, отклонений в вертикальном сечении, отклонений от плоскостности поверхностей, отклонений от формы заданного профиля, поверхности и конструкций, технологического оборудования, линейных зданий и сооружении... 61
7.8 Схемы и методы измерения линейных и угловых размеров, отклонений в плане и высоте профиля, формы и взаимного положения поверхностей деталей, изделий, конструкций и технологической оснастки, изготавливаемых при производстве СМР непосредственно на монтажном горизонте, строительных площадках зданий и сооружений…………………………………………………………….. 65
7.9 Требования к местам, контрольным точкам, сечениям используемым при измерении длины, ширины, толщины, диаметра, угловым размерам, а также их отклонениям………………………………….. 76
8 Геодезический контроль точности геометрических параметров зданий и сооружений……………..………………………………………………….... 77
8.1 Организация геодезического контроля……………………………… 77
8.2 Требования к точности измерений методам контроля выполняемых при геодезическом контроле геометрических параметров зданий… 79 8.3 Содержание и проведение геодезического контроля геометрических параметров зданий и сооружений Проект СТО НОСТРОЙ 37 - 2013 V ……………………………. 80
9. Регистрация, обработка и формы представления результатов измерений 82
9.1 Обработка результатов многократных измерений…………………. 82
9.2 Формы представления результата измерения……………………… 83
10 Оценка соответствия точности измерений…………….………………… 86
11 Использование характеристик точности измерений при оценке соответствия геометрических параметров зданий и сооружений требованиям проектной документации…………………………………………………… 88
Приложение А (рекомендуемое) Методика измерения условных горизонтальных координат контрольных точек разбивочных осей и их отклонений от проектных требований на исходном и монтажных горизонтах электронным тахеометром с пунктов внешней и внутренней разбивочных сетей при возведении зданий и сооружений………….……………………. 90
Приложение Б (рекомендуемое) Методика измерения горизонтальных и вертикальных условных координат контрольных точек разбивочных вертикальных осей теодолитом и нивелиром при возведении зданий и сооружений………..…………… 107
Приложение В (рекомендуемое) Методика измерения теодолитом отклонений от вертикали строительных конструкций и элементов зданий и сооружений ……………………….. 123
Приложение Г (рекомендуемое) Характеристики точности геометрических параметров зданий и сооружений……………………. 133
Приложение Д (рекомендуемое) Определение точности измерений при многократных прямых измерениях………………………… 137
Приложение Е (рекомендуемое) Определение характеристик качества измерений в полевых условиях для нивелира………………… 144
Приложение Ж (рекомендуемое) Введение поправок относительно условий измерения…………………………………..…………… 158
Приложение И (справочное) Примерные схемы построения внешней разбивочной сети здания, сооружения Проект СТО НОСТРОЙ 37 - 2013 VI ………………………… 162
Приложение К (рекомендуемое) Форма технического задания на разработку проекта производства геодезических работ………… 163
Приложение Л (справочное) Значения предельных погрешностей по- строения межосевых размеров большепролётных промышленных сооружений…………………………….. 166
Приложение М (рекомендуемое) Порядок назначения методов контроля геометрических параметров зданий и сооружений……….. 168
Приложение Н (рекомендуемое) Общие правила составления разделов ППР и ППГР по геодезическому контролю точности гео- метрических параметров…………………………………… 174
Приложение П (рекомендуемое) Общие правила проведения геодезической исполнительной съёмки строящегося здания или сооружения и регистрации её результатов…………………… 181
Библиография……….……………………………………………………………. 199
Лекция №
Процедура принятия решений
Для решения слабо структурированных проблем используется методология системного анализа, системы поддержки принятия решений (СППР). Рассмотрим технологию применения системного анализа к решению сложных задач.
Процедура принятия решений согласно [2] включает следующие основные этапы:
1. формулировка проблемной ситуации;
2. определение целей;
3. определение критериев достижения целей;
4. построение моделей для обоснования решений;
5. поиск оптимального (допустимого) варианта решения;
6. согласование решения;
7. подготовка решения к реализации;
8. утверждение решения;
9. управление ходом реализации решения;
10. проверка эффективности решения.
Для многофакторного анализа, алгоритм можно описать и точнее:
1. описание условий (факторов) существования проблем, И, ИЛИ и НЕ связывание между условиями;
2. отрицание условий, нахождение любых технически возможных путей. Для решения нужен хотя бы один единственный путь. Все И меняются на ИЛИ, ИЛИ меняются на И, а НЕ меняются на подтверждение, подтверждение меняется на НЕ-связывание;
3. рекурсивный анализ вытекающих проблем из найденных путей, то есть п. 1 и п. 2 заново для каждой подпроблемы;
4. оценка всех найденных путей решений по критериям исходящих подпроблем, сведенным к материальной или иной общей стоимости.
Методика по Квейду
1. постановка задачи – включает определение проблемы, выявление целей и определение границ задачи;
2. поиск – включает сбор сведений и определение альтернативных средств достижения целей;
3. толкование – построение модели и её использование;
4. реализация – агрегирование предпочтительной альтернативы или курса действий;
5. подтверждение – экспериментальная проверка решения.
Методика Янга
1. определение целей организации;
2. выявление проблем организации;
3. исследование проблем и постановка диагноза;
4. поиск решения проблемы;
5. оценка всех альтернатив и выбор наилучшей;
6. согласование решений в организации;
7. утверждение решения;
8. подготовка к вводу;
9. управление применением решения;
10. проверка эффективности решения.
Системный анализ
· 1) в узком смысле совокупность методологических средств, используемых для подготовки и обоснования решений по сложным проблемам политического, военного, социального, экономического, научного, технического характера. 2) В широком смысле термин «С. а.» иногда… … Философская энциклопедия
· Системный анализ — Системный анализ научный метод познания, представляющий собой последовательность действий по установлению структурных связей между переменными или элементами исследуемой системы. Опирается на комплекс общенаучных, экспериментальных,… … Википедия
· системный анализ — Совокупность методологических средств, используемых для подготовки и обоснования решений по сложным проблемам различного характера. Он опирается на системный подход, а также на ряд математических методов и современных методов управления. Основная … Справочник технического переводчика
· Системный Анализ — (systems analysis) Изучение или анализ задач и проблем системы, направленные на развитие и усовершенствование этой системы путем внедрения компьютеров. Системный анализ завершается точными рекомендациями того, что надо сделать, определением… … Словарь бизнес-терминов
· СИСТЕМНЫЙ АНАЛИЗ — СИСТЕМНЫЙ АНАЛИЗ, совокупность методологических средств, используемых для подготовки и обоснования решений по сложным проблемам политического, военного, социального, экономического, научного и технического характера. Опирается на системный подход … Современная энциклопедия
· СИСТЕМНЫЙ АНАЛИЗ — совокупность методологических средств, используемых для подготовки и обоснования решений по сложным проблемам политического, военного, социального, экономического, научного и технического характера. Опирается на системный подход, а также на ряд… … Большой Энциклопедический словарь
· Системный анализ — СИСТЕМНЫЙ АНАЛИЗ, совокупность методологических средств, используемых для подготовки и обоснования решений по сложным проблемам политического, военного, социального, экономического, научного и технического характера. Опирается на системный подход …
· Иллюстрированный энциклопедический словарь
· СИСТЕМНЫЙ АНАЛИЗ — (от греч. systema целое, составленное из частей и анализ) совокупность методов и средств исследования сложных, многоуровневых и многокомпонентных систем, объектов, процессов, опирающихся на комплексный подход, учет взаимосвязей и взаимодействий… … Экономический словарь
· системный анализ — Исследование функциональных и структурных взаимосвязей природных явлений, рассматриваемых в качестве системы, в которой определяются границы, возможности использования, а также положение и роль в следующей по рангу природной системе. Syn.:… … Словарь по географии
· СИСТЕМНЫЙ АНАЛИЗ — СИСТЕМНЫЙ АНАЛИЗ, метод анализа процесса или операции для улучшения производительности, в частности, с помощью КОМПЬЮТЕРА, который способен оперировать большим числом независимых действий, объединенных в одну сложную операцию … Научно-технический энциклопедический словарь
Книги
СИСТЕМНЫЙ АНАЛИЗ
это совокупность методов и средств, используемых при исследовании и констру -ирования сложных и сверхсложных объектов, прежде всегометодов выработки, принятия и обоснования решений при проектировании, создании и управлениисоциальными, экономическими, человеко-машинными и техническими системами. В литературе понятие С. а. иногда отождествляется с понятием системного подхода, но такая обобщенная трактовка С. а. вряд ли оправданна.
С. а. возник в 1960- х как результат развития исследования операций и системотехники. Теоретическую и методологическую основу С. а. составляют системный подход и общая теория систем. С. а. применяется, главным образом, к исследованию искусственных (возникших при участии человека) систем, причем в таких системах важная роль принадлежит деятельности человека. Использование методов С. а. для решения исследовательских и управленческих проблем необходимо, прежде всего, потому, что впроцессе принятия решений приходится осуществлять выбор в условиях неопределенности, котораясвязана с наличием факторов, не поддающихся строгой количественной оценке. Процедуры и методы С. а. направлены на выдвижение альтернативных ввариантов решения проблемы, на выявление масштабовнеопределенности по каждому из вариантов и на сопоставление вариантов по тем или иным критериямэффективности. Согласно принципам С. а., возникающая перед обществом та или иная сложная проблема(прежде всего проблема управления) должна быть рассмотрена как нечто целое, как система вовзаимодействии всех ее компонентов. Для принятия решения управлении этой системой необходимоопределить ее Ц е л ь, цели ее отдельных подсистем и множество альтернатив достижения этих целей, которые сопоставляются по определенным критериям эффективности, и в результате выбирается наиболееприемлемый для данной ситуации способ управления. Центральной процедурой в С. а. являетсяпостроение обобщенной модели (или моделей), отображающей все факторы и взаимосвязи реальнойситуации, которые могут проявиться в процессе осуществления решения. Полученная модель исследуется сцелью выяснения близости результата применения того или иного из альтернативных вариантов действий кжелаемому, сравнительных затрат ресурсов по каждому из вариантов, степени чувствительности модели кразличным нежелательным внешним воздействиям. С. а. опирается на ряд прикладных математическихдисциплин и методов, широко используемых в современной деятельности управления. Техническая основаС. а. — современные компьютеры и информационные системы. В С. а. широко используются методысистемной динамики, теории игр, эвристического программирования, имитационного моделирования, программно-целевого управления и т.д. Важной особенностью С. а. является единство используемых в немформализованных и неформализованных средств и методов исследования.
НОРМИРОВАНИЕ ТОЧНОСТИ И ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ
Дата: 2019-02-19, просмотров: 427.