Коэффициент теплопередачи рассчитываем, исходя из того, что при установившемся процессе передачи тепла справедливо равенство:
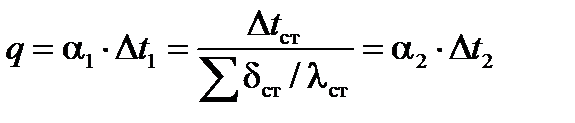 (1.12)
(1.12)
Коэффициент теплопередачи К в [Вт/(м2 К)] можно рассчитать по уравнению:
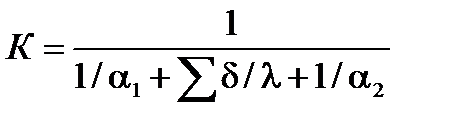 , (1.13)
, (1.13)
где q – удельная тепловая нагрузка, Вт/м2; q = Q/F;
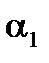 и
и 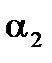 – коэффициенты теплоотдачи от конденсирующегося пара к стенке и от стенки к кипящему раствору соответственно, Вт/(м2∙К);
– коэффициенты теплоотдачи от конденсирующегося пара к стенке и от стенки к кипящему раствору соответственно, Вт/(м2∙К);
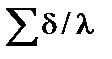 – сумма термических сопротивлений стенки загрязнений и накипи, (м2∙К/Вт);
– сумма термических сопротивлений стенки загрязнений и накипи, (м2∙К/Вт);
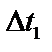 – разность температур между греющим паром и стенкой со стороны пара в первом корпусе, ºС;
– разность температур между греющим паром и стенкой со стороны пара в первом корпусе, ºС;
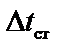 – перепад температур на стенке, ºС;
– перепад температур на стенке, ºС;
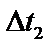 – разность между температурой стенки со стороны раствора и температурой кипения раствора, °С.
– разность между температурой стенки со стороны раствора и температурой кипения раствора, °С.
Коэффициент теплоотдачи 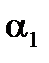 рассчитываем по уравнению:
рассчитываем по уравнению:
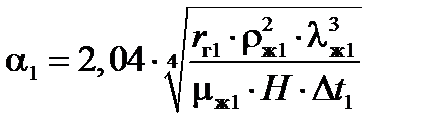 , (1.14)
, (1.14)
где 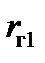 – теплота конденсации греющего пара, Дж/кг;
– теплота конденсации греющего пара, Дж/кг;
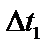 – разность температур конденсата пара и стенки, ºС;
– разность температур конденсата пара и стенки, ºС;
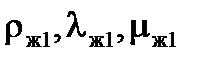 – соответственно плотность, кг/м3, теплопроводность Вт/(м∙К) и вязкость конденсата, Па∙с, при средней температуре плёнки:
– соответственно плотность, кг/м3, теплопроводность Вт/(м∙К) и вязкость конденсата, Па∙с, при средней температуре плёнки:
Первоначально принимаем ∆t1=1,0 °С.
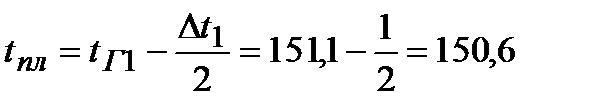 °С
°С
Значения физических величин конденсата берём при tпл = 150,6 ºС.
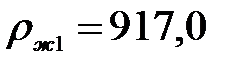 кг/м3
кг/м3
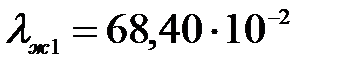 Вт/(м·К)
Вт/(м·К)
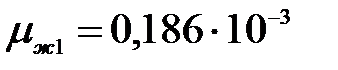 Па·с
Па·с
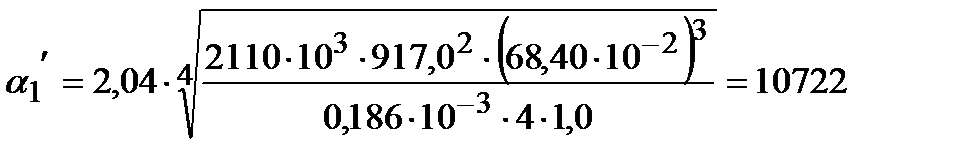 Вт/(м2·К)
Вт/(м2·К)
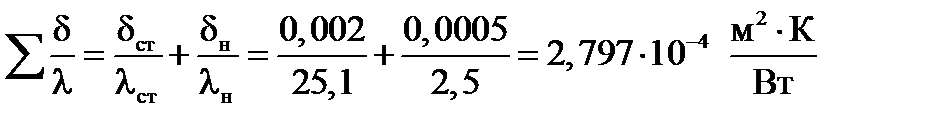
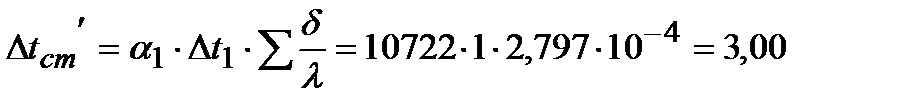 °С
°С
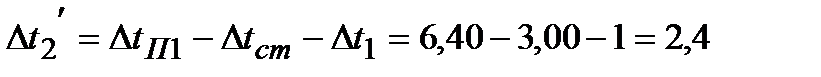 °С
°С
Коэффициент теплоотдачи от стенки к кипящему раствору 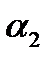 в условиях его естественной циркуляции для пузырькового режима в вертикальных трубах равен:
в условиях его естественной циркуляции для пузырькового режима в вертикальных трубах равен:
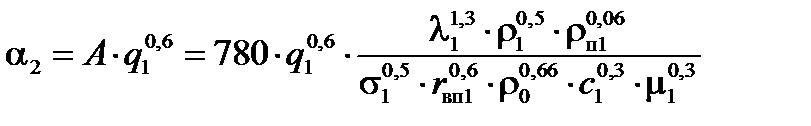 , (1.15)
, (1.15)
где 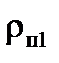 – плотность греющего пара в первом корпусе,
– плотность греющего пара в первом корпусе, 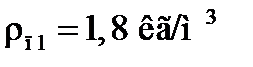
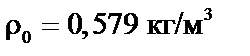 – плотность пара при атмосферном давлении;
– плотность пара при атмосферном давлении; 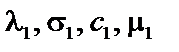 – соответственно, теплопроводность, поверхностное натяжение, теплоемкость и вязкость раствора в первом корпусе.
– соответственно, теплопроводность, поверхностное натяжение, теплоемкость и вязкость раствора в первом корпусе.
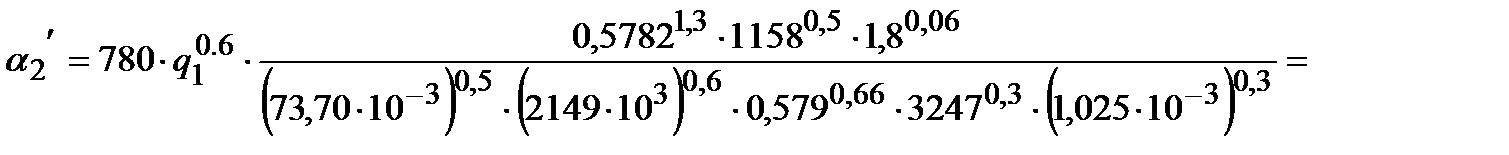
 Вт/(м2·К)
Вт/(м2·К)
Значения величин, характеризующих свойства растворов CaCl2, представлены в таблице 1.5.
| Параметр | Корпус | ||
| 1 | 2 | 3 | |
Плотность раствора, 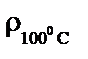 , кг/м3 , кг/м3
| 1158 | 1207 | 1304 |
Вязкость раствора, 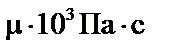
| 1,025 | 1,035 | 1,050 |
Теплопроводность раствора, 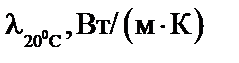
| 0,5782 | 0,5717 | 0,5578 |
Поверхностное натяжение, 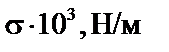
| 73,70 | – | – |
Теплоёмкость раствора, 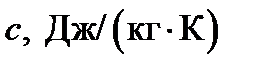
| 3247 | 2996 | 2577 |
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
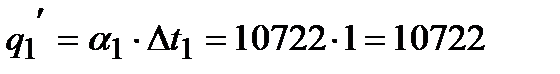 Вт/м2
Вт/м2
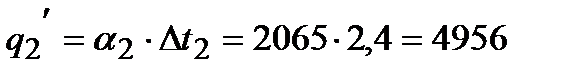 Вт/м2
Вт/м2
Как видим 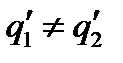
Для второго приближения примем ∆t1=0,5 °С
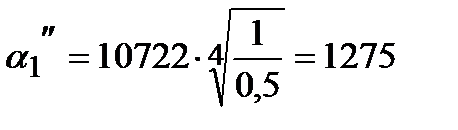 Вт/(м2·К)
Вт/(м2·К)
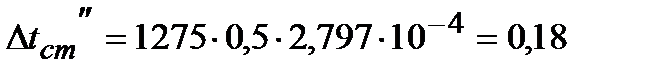 °С
°С
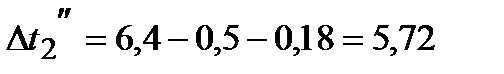 °С
°С
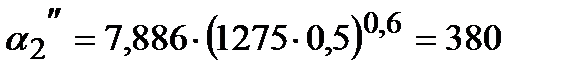 Вт/м2
Вт/м2
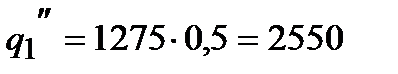 Вт/м2
Вт/м2
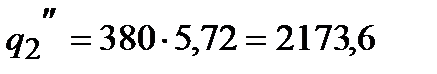 Вт/м2
Вт/м2
Очевидно, что 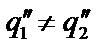
Для определения 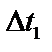 строим графическую зависимость тепловой нагрузки q от разности температур между паром и стенкой (см. рис. 1.1) и определяем
строим графическую зависимость тепловой нагрузки q от разности температур между паром и стенкой (см. рис. 1.1) и определяем 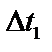 = 0,47 ºС.
= 0,47 ºС.
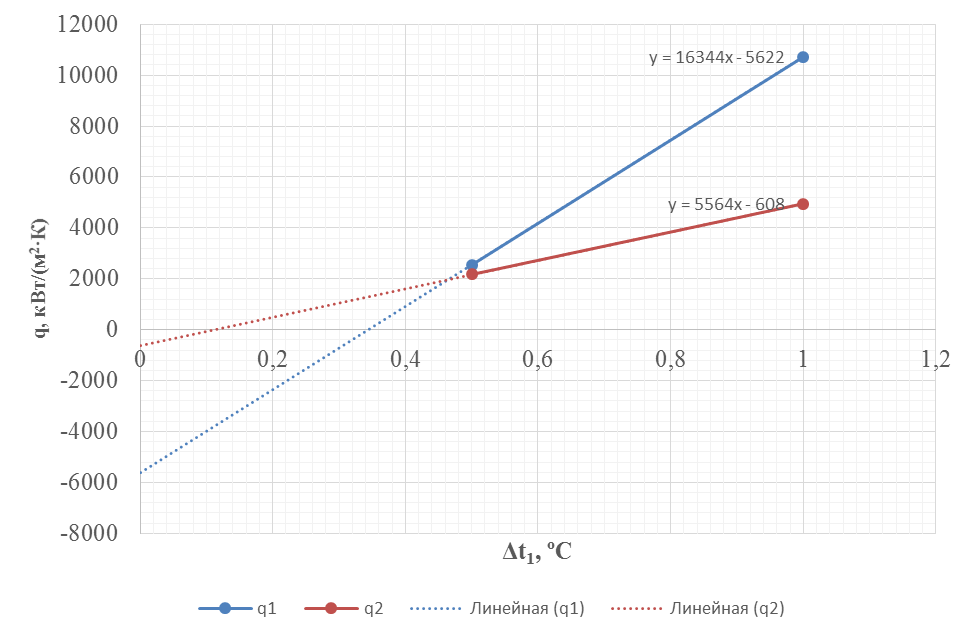
Рисунок 1.1 – Зависимость тепловой нагрузки от разности температур Δt1, для 1 корпуса
Проверка:
∆t1=0,47 °С
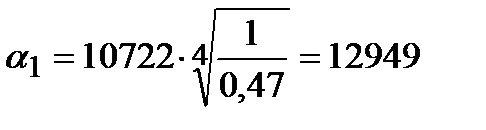 Вт/(м2·К)
Вт/(м2·К)
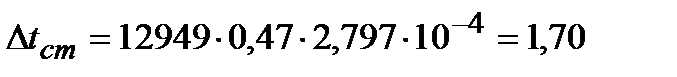 °С
°С
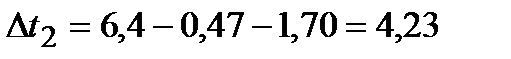 °С
°С
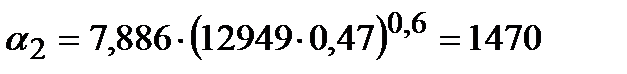 Вт/м2
Вт/м2
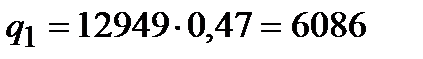 Вт/м2
Вт/м2
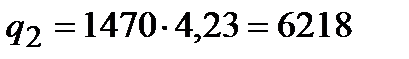 Вт/м2
Вт/м2
Как видим 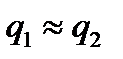
Рассчитываем коэффициент теплопередачи К1 в первом корпусе:
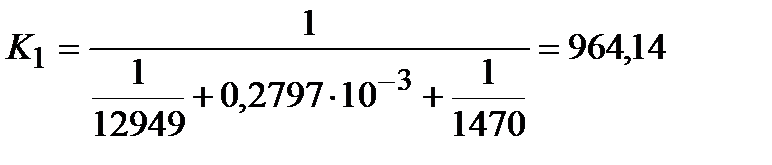 Вт/(м2·К)
Вт/(м2·К)
Коэффициент теплопередачи для второго корпуса К2 и третьего К3 можно рассчитывать так же, как и коэффициент К1 или с достаточной точностью воспользоваться соотношением коэффициентов, полученных из практики ведения процессов выпаривания. Эти соотношения варьируются в широких пределах:
К1 : К2 : К3 = 1 : (0,85 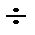 0,5)
0,5) 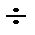 (0,7
(0,7 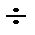 0,3)
0,3)
Принимаем значения коэффициентов по верхним пределам.
К1 : К2 : К3 = 1 ÷ 0,5 ÷ 0,3
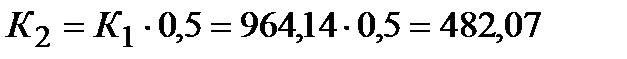 Вт/(м2·К)
Вт/(м2·К)
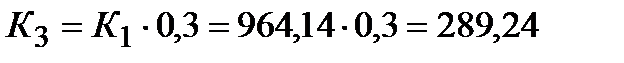 Вт/(м2·К)
Вт/(м2·К)
Дата: 2019-02-19, просмотров: 316.