Явление общественной жизни, изучаемые статистикой, находятся в постоянном развитии и изменении. От месяца к месяцу, от года к году изменяется численность населения, его состав, изменяется уровень производства, продаж, прибыль. Поэтому одной из важнейших задач статистики является изучение изменений общественных явлений во времени. Эту задачу статистика решает с помощью построения и анализа рядов динамики.
Ряд динамики (динамический ряд) – это ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующего изменение общественных явлений во времени.
В каждом ряду динамики имеется два основных элемента:
время (t) и уровни ряда (y)
Уровни ряда – это показатели, числовые значения которых составляют динамический ряд.
Время – это моменты (даты) или периоды, к которым относятся уровни.
Соответственно, в зависимости от того, как выражено время, различают два вида рядов динамики : моментные и интервальные.
Моментным называется ряд динамики, отображающий состояние изучаемого явления на определённые даты (моменты) времени . Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемого явления. Поэтому уровни моментного ряда нельзя суммировать, т.к. возникает повторный счёт.
Интервальным называется ряд динамики, отображающий итоги изучаемого явления за отдельные периоды (интервалы) времени) . Уровни интервального ряда можно суммировать, т.к. получается итог явления за более крупный период.
Анализируя ряд динамики, принято рассчитывать его средний уровень. Способ расчёта зависит от вида ряда динамики.
Средний уровень моментного ряда определяется по средней хронологической :
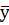= ( ½ У1 + У2 + У3 + … + ½ У n ) \ n – 1 , где n – число уровней
Средний уровень интервального ряда определяется по средней арифметической простой :
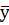= ( У1 + У2 + У3 + … Уn ) \ n
Вопрос 23, 24. Цепной способ расчёта показателей ряда динамики.
Базисный способ расчёта показателей ряда динамики.
Анализ рядов динамики может производиться двумя способами : цепным и базисным.
Если каждый уровень ряда сравнивается с предыдущим, то получают цепные показатели, а если все уровни ряда сравниваются с одним и тем же первоначальным уровнем, то полученные показатели называются базисными.
Показатели ряда динамики
| Название и условное обозначение | Цепной способ расчёта | Базисный способ расчёта | Что показывает |
| Абсолютный прирост ∆У | ∆У = Уn – Уn-1 | ∆У = Уn - Уо | На сколько изменился (увеличился или уменьшился) следующий уровень по сравнению с предыдущим или базисным уровнем |
| Темп роста Тр | Тр = Уn \ У n-1 Тр = (Уn \ Уn-1 ) х 100 % Среднегодовой темп роста Тр = √ Тр1 х Тр2 х …Тn | Тр = Уn \ Уo Тр = (Уn \ Уo) х 100% Среднегодовой темп роста Тр = √Уn \ Уо | Во сколько раз следующий уровень больше или меньше предыдущего или базисного уровня. Сколько процентов составил следующий уровень от предыдущего или базисного уровня, если последний взять за 100%. |
| Темп прироста Т∆ | Т∆ = Тр – 1 Т∆ = Тр – 100 % или Т∆ = ∆У \ У n-1 х 100 % Среднегодовой темп прироста Т∆ = Тр – 100% | Т∆ = Тр – 1 Т∆ = Тр – 100% или Т∆ = ∆У \ Уо х 100% Среднегодовой темп прироста Т∆ = Тр – 100 % | На сколько в долях единицы изменился следующий уровень по сравнению с предыдущим или базисным уровнем. На сколько процентов изменился следующий уровень по сравнению с предыдущим или базисным уровнем. |
| Абсолютное значение одного процента прироста А% | А% = У n-1 \ 100 или А% = ∆У \ Т ∆ | Не имеет экономического смысла | Сотую часть предыдущего уровня или на сколько в абсолютном выражении изменится следующий уровень, если он изменится только на 1 % |
Дата: 2019-02-25, просмотров: 189.
